一种改进的半监督谱聚类算法

王 磊

（商洛学院 现代教育技术中心，陕西商洛 726000）

近年来有关谱聚类算法的应用研究受到了国内外学者的广泛关注，并且已经在多个领域得到了较好的应用,如：图像分割[1-2]，文本语义分析[3-4]等。但该算法在实际应用中仍然存在一些亟待解决的问题，例如：由于传统谱聚类通常采用K-means算法对特征向量进行聚类，导致算法对初始聚类中心较敏感[5]，稳定性较低、准确性不高，并难以应用于大规模数据处理等，这些问题极大的阻碍了该算法的进一步应用与发展。由此，本文在深入研究谱聚类算法、Bayes决策理论及半监督学习方法的基础上，提出了一种结合Bayes决策的半监督谱聚类算法。其主要思想是利用Bayes决策的距离学习理论对相似度矩阵的内容进行适当调整；然后，利用半监督K-means聚类对调整后的特征向量进行聚类划分，进一步提高谱聚类算法的稳定性与准确性。

1 谱聚类算法

谱聚类算法是建立在谱图理论基础之上，其基本内容是：首先根据给定的数据集按照一定的相似度测量规则定义一个描述成对数据点相似度的相似度矩阵，并计算矩阵的特征向量和特征值，然后选择合适的特征向量聚类成不同的数据点[6-7]，是一种点对聚类算法，对数据聚类具有很好的应用前景。由于谱聚类算法建立在图论中的谱图理论基础上，其本质是将聚类问题转化为图的最优划分问题，即：成求解Laplacian矩阵或相似度矩阵的谱分解问题[8]。与传统的聚类算法相比，它具有能在任意形状的样本空间上聚类并且收敛于全局最优解的优点。谱聚类算法最初用于计算机视觉、VLSI设计等领域，最近才开始用于机器学习中，并迅速成为国际上机器学习领域的研究热点。

在谱聚类算法中，设 X={x1，x2，…，xn}为待聚类的样本集，相似度矩阵通常被定义为

其中d(xi,xj)一般取欧式距离（即||xi-xj||2），σ为事先确定的参数。

根据不同的谱映射方法及准则函数，谱聚类算法衍生出许多具体实现方法，这里给出当前较为常用的一种实现方法——NJW算法[9],该算法为：首先选取Laplacian矩阵的前k个最大特征值所对应的特征向量，并使其与原样本集在 Rk空间中构成一一对应关系，然后在Rk空间中进行聚类。算法的具体描述如下：

输入：样本集 X={x1，x2，…，xn}及聚类数目 k

1）建立相似度矩阵 W∈Rn×n，其中 Wij=exp(d(xi，xj)/2σ2),i≠j，且 Wij=0；

2）构造 Laplacian 矩阵 L=D-1/2WD-1/2，其中为对角矩阵；

3）计算Laplacian矩阵L的特征向量与特征值，选取其前k个最大特征值所对应的特征向量z1，z2，…，zn，构造矩阵 Z=[z1，z2，…，zk]∈Rn×k；

5）将矩阵Y中的每一行视为空间Rn*k中的一个样本，使用K-means算法对其进行聚类，将其划分为k类；

6）将初始样本点xi划分为第j类，当且仅当矩阵Y 的第i行被划分到聚类j中；

输出：输入样本集X中所有样本点对应的类标{l1，l2，…，lN}。

2 结合Bayse决策的半监督谱聚类算法

2.1 基于Bayes决策的距离学习方法

特征向量分布情况的好坏直接影响着谱聚类算法的稳定性强弱，而决定特征向量分布的关键因素在于相似度矩阵的取值是否合适，即使不同类的样本间相似度足够小，而同类的样本间相似度足够大。针对该问题，本文在深入研究Bayes决策理论及半监督学习理论的基础上，提出了一种新的基于距离的半监督学习方法——基于Bayes决策的距离学习方法，目的是改善用于进行聚类的特征向量的分布情况。

Bayes决策理论的基本思路[10]：已知类别数为c，样本x属于每一类的先验概率P(ωi)及类条件概率密度函数P(x|ωi)(各类别状态用ωi来表示，i=1，2，…，c）,根据 Bayes 公式得到属于每类的后验概率P(ωi|x)，然后由后验概率的大小值确定每个样本x的类属。

设 D1，D2，…，Dc为样本空间S的一个划分,如果以 P(ωi)表示事件 Di发生的概率，且 P(ωi)＞0,(i=1，2，…，c)。对于任一事件 x，如果 P(x)＞0 则有[11]

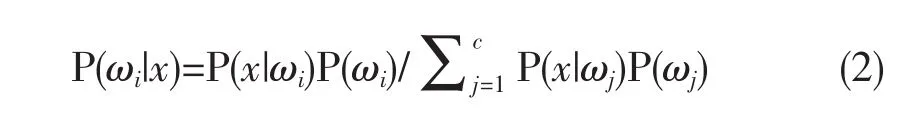
由此可以得出一种使错误率最小的分类规则，称之为基于最小错误率的Bayes决策。其具体描述如式(3)。

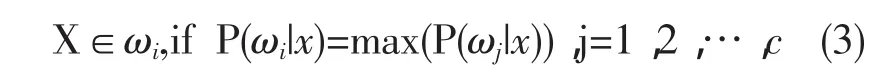
这里给出基于Bayes决策的距离学习方法的基本思路如下：

设有样本集 X={x1，x2，…，xn}，其中 n 为样本数，xi=[xi1，xi2，…，xim]T，m 为样本的特征数或维数。已知的成对约束信息分别用M和C来表示，其中M表示must-links集合，C表示cannot-links集合，其定义如下：

设已知样本集X的相似度矩阵W，定义集合U为矩阵W中除对角线元素之外的其他所有元素的并集，集合WM及WC分别表示集合M与集合C中所有点对在矩阵W中对应数值的并集，集合WV为集合WM与WC的并集，其数学描述如下：

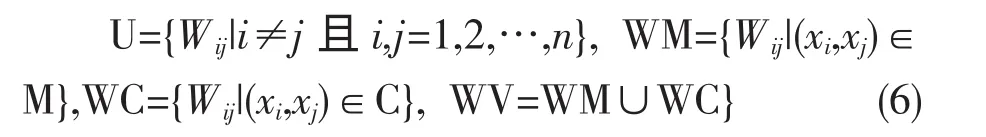
其中Wij为W矩阵中样本xi和样本xj的d(xi,xj)距离。

1）计算所有样本点之间的相似度矩阵W:Wij=exp(d(xi,xj)/2σ2)

2）按照式(6)分别计算集合 U、WM、WC、WV；

3）分别计算集合WV中任意元素属于集合 WM 的先验概率 P(ωm)、条件概率 P(w|ωm)以及属于集合WC的先验概率P(ωc)、条件概率 P(w|ωc)；

综上所述，基于Bayes决策的距离测度函数的基本思想是：把集合WV的元素作为训练样本，建立基于最小错误率的Bayes决策分类器；利用该分类器对相似度矩阵W中可分元素（即可计算其后验概率）进行分类，将其划分至集合WM及WC中；利用类别信息及后验概率，依据所示距离测度函数对矩阵W的内容进行调整。

2.2 成对约束的K-means聚类算法

经分析，传统谱聚类算法稳定性较低，其中一个很重要的原因是进行特征向量聚类的聚类算法（通常是K-means）对初始聚类中心较敏感引起的。针对该问题，本文采用一种经典的基于成对约束的半监督聚类算法——成对约束的K-means聚类（Constrained-K-means）[12]来完成特征向量的聚类。该算法首先利用少量的标记样本产生初始聚类中心；然后，使用前述标记的样本以出成对约束的形式来引导整个算法的迭代过程（如表2）。由于其效率较高，实现简单，并且能够一定程度上提高K-means算法的稳定性，因而已被广泛应用于各个领域。带约束的K-means聚类算法的具体描述如下：

2）若x∈S，则其类标签不变；否则，根据相似度规则，将其分配到离它最近的聚类中，并修改类标签；

4）若聚类中心不再发生改变，算法结束；否则跳转到步骤2）;

输出：样本集X中所有样本点对应的类标签{l1，l2，…，lN}。

3 实验分析

3.1 实验数据

选取两幅人工合成纹理图像作为实验图像（如图1、表1）。所有的实验都是在相同的硬件环境中进行的（硬件环境：Intel Core(TM)2，1.86GHz With 1G memory），实验软件：MATLAB 7.8.0(R2009a)。

其中，对于这两幅实验图像，提取三个图像特征，分别是：3维RGB颜色特征、2维空间特征及3维纹理特征，其中纹理特征采用灰度共生矩阵法，分别取能量、熵和对比度在 0°、45°、90°、1350这四个方向上的均值所构成的3维纹理特征，图像的量化等级为8灰度级，滑动窗口的大小为9*9；相似度函数如式(9)所示，其中各高斯参数的确定方法为经验值与网格法相结合：颜色参数σc=0.03、空间参数σs=70、纹理参数σt的取值范围为0.03-0.30；具体参数设置见表2。

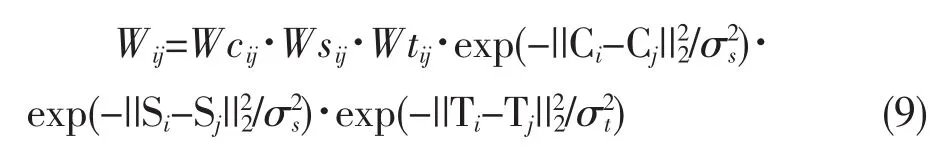
其中，Wij表示样本i和j之间的相似度，Wcij、Wsij及 Wtij分别表示样本 i和 j之间的颜色、空间及纹理相似度，C、S及T分别表示颜色特征、空间特征及纹理特征。

图1 实验用图

表1 人工合成纹理图

表2 实验参数

3.2 实验结果

在图2中，可以清楚的看到，传统谱聚类在两副图像上的分割效果都很一般，存在着大量错分情况；而采用本文方法的分割效果要明显优于传统谱聚类算法，尤其是对二类人工合成纹理图像的分割结果和理想的人工分割结果相差无几，很明显本文方法较传统谱聚类在背景部分具有更好的区域一致性与更少的离散点分布。

在图3中，为了体现本文算法稳定性的优势，对三幅人工合成图像进行22次试验统计其正确率分布情况。显然，本文算法在22次图像分割实验中正确率变化幅度较传统谱聚类更加平稳。

在表3中，可以看出本文算法的平均正确率较传统谱聚类算法有了明显的提高，同时正确率方差也控制在较低水平上，稳定性得到了数倍的提高。

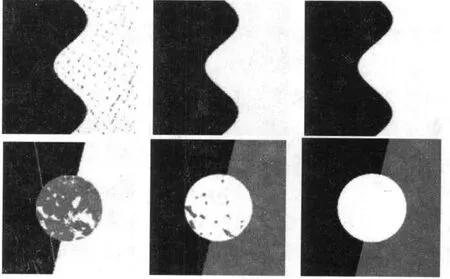
图2 聚类结果

图3 正确率分布

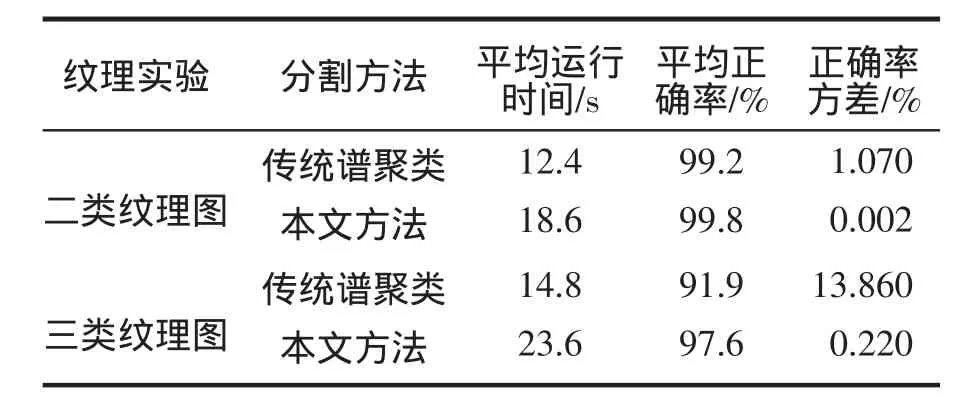
表3 对比试验结果

4 结论

针对谱聚类算法稳定性较低、准确性不高的缺点，本文深入研究谱聚类算法、Bayes决策理论以及半监督学习方法，提出了一种结合Bayes决策的半监督谱聚类算法。经仿真实验证明，本文方法较传统谱聚类在稳定性及准确率方面都有显著提高，达到了预期目的。但该方法仍然存在不足之处，例如，如何选取半监督信息、如何选择最优核参数等，还需要进一步探讨。

[1]高 倩,戴月明.用于文本聚类的模糊谱聚类算法[J].计算机工程与应用,2010,46(3):142-144.

[2]林 立,胡 侠,朱俊彦.基于谱聚类的多文档摘要新方法[J].计算机工程,2010,36(22):64-66.

[3]Hebert P,Macaire L.Spatial-color pixel classification by spectral clustering for color image segmentation[C]//information and communication technologies ICTTA 3rd International Conference on,2008:1-5.

[4]Feng Sun,Jinpeng He.The remote-sensing image segmentation using textons in the Normalized Cuts framework [C].Mechatronicsand Automation,2009 ICMA 2009 International Conference on,2009:1877-1881.

[5]朱强生,何华灿,周延泉.谱聚类算法对输入数据顺序的敏感性[J].计算机应用研究,2007,24(4):62-63.

[6]施培蓓,郭玉堂,胡玉娟.初始化独立的谱聚类算法[J].计算机工程与应用,2010,46(25):134-137.

[7]沈亚田,沈夏炯,张 磊.基于图划分的谱聚类算法在文本挖掘中应用[J].计算机技术与发展,2009,19(5):96-98.

[8]Von Luxburg U.A Tutorial on spectral clustering[J].Statistics and Computing,2007:395-416.

[9]Ng A Y,Jordan M I,Weiss Y.On spectral clustering:analysis and an algorithm[M].Advances in Neural Information Processing Systems,Cambridge,MIT Press,2002:849-856.

[10]边肇祺,张学工.模式识别[M].2版.北京:清华大学出版社,2000.

[11]Huan Ruohong,Yun Pan,KejiMao.SAR image target recognition based on NMF feature extraction and Bayesian decision fusion[C].Geoscience and Remote Sensing(IITA-GRS),2010 Second IITA International Conference on,2010:496-499.

[12]Basu S,Banerje e A,Mooney R.Semi-supervised clustering by Seeding[C].Machine learning-international workshop then conference on,2002:19-26.