柱矢量光束的角动量

刘宝盈

（商洛学院 物理与电子信息工程系，陕西商洛 726000）

众所周知，光束具有能量、线动量和角动量。1936年Beth通过实验观察到了光场中光子的角动量，即自旋角动量[1]。1992年，Allen等研究了近轴条件下线偏振的拉盖尔——高斯光束（LG）的轨道角量[2]，发现LG光束的角动量可以分成两部分：一部分取决于光的偏振态，即仅与光子的自旋量子数相关的角动量，称为光束的自旋角动量；另一部分取决于光传播时的螺旋形波前相位，即仅与角向量子数相关的角动量，称为光束的轨道角动量。随后他们研究了非近轴拉盖尔——高斯轴对称矢量光束[5-8]，发现自旋角动量只与偏振有关而轨道角动量只与螺旋相位波前有关这一描述近轴光束角动量的理论对非近轴光束已不适合[3-6]。O'Neil等研究发现，非近轴光束在与囚禁在光轴附近的双折射微粒相互作用时，其自旋角动量和轨道角动量作用截然不同，自旋角动量的传递使微粒绕自轴旋转，而轨道角动量的传递则使微粒绕光轴旋转[7]。实验还发现，在非均匀各向同性介质中自旋角动量可以转换为轨道角动量[8]，通过一个高数值孔径，近轴光束的自旋角动量也能转换为非近轴光束的轨道角动量[9]。李春芳利用他建立的光束表示理论[10]研究了具有整体偏振特性的一类非近轴光束的自旋和轨道角动量，分析了两者之间的区别和联系[11]。这些理论研究和实验结果都说明光束的自旋和轨道角动量既有区别又密切相关。

本文按照光束自旋角动量和轨道角动量的一般定义，分析了具有轴对称偏振特性和强度分布的柱矢量光束的角动量，发现柱矢量光束的自旋角动量是光的内在性质，只与偏振有关，而轨道角动量不仅与角向量子数（即光束传播时的螺旋波前相位）有关而且与偏振有关，即使在近轴近似条件下光束的角动量也不能自然地分为只与偏振有关的自旋角动量和只与角向量子数相关的轨道角动量两部分。

1 自由空间光束的角动量

根据经典电磁理论，在自由空间中传播的光束其能量、线动量和角动量的表达式为[11-12]：

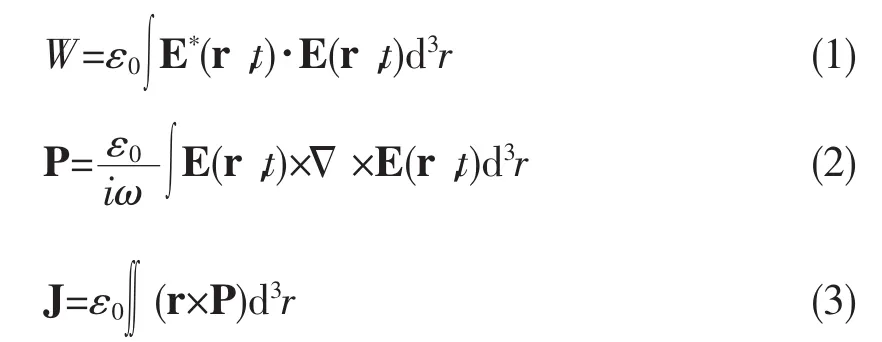
为了方便分析将公式(1)(2)(3)变换到动量空间。为此，设在自由空间的任一光束的电场强度矢量为[11]

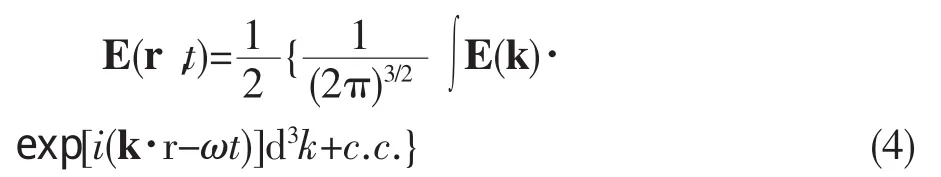
式中k为波矢量，k=kxex+kyey+kzez，波矢量的大小k与角频率ω之间的关系为k2=ε0μ0ω2。E(k)为动量空间的电场强度矢量，该光束的能量为

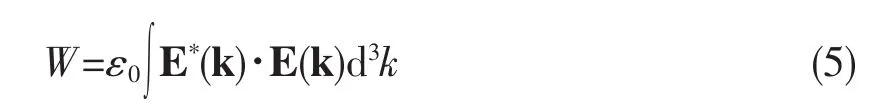
利用矢量代数公式 a(a×b)=(a×c)b-(a×b)c 可知动量P包含两项，对应的角动量也分成两项，其中一项与参照点的选择有关，将之称为轨道角动量，用L表示；而另一项与参照点的选择无关，将之称为自旋角动量，用S表示，则

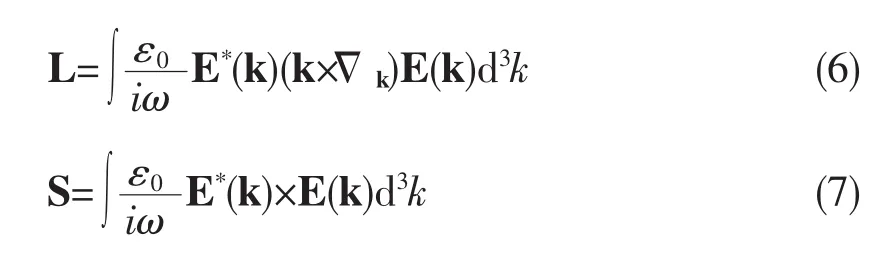
因此光束的角动量为

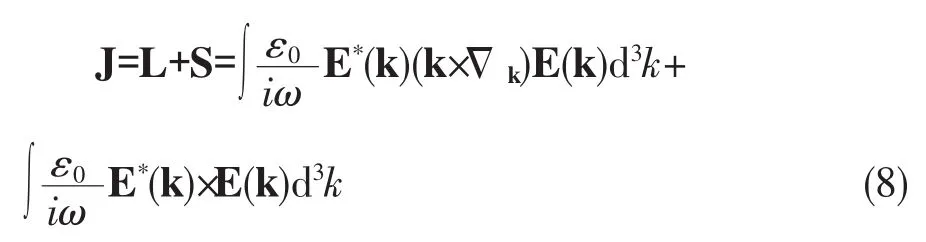
2 柱矢量光束的角动量

对于自由空间中任一束沿正z轴方向传播的单色光束，其电场强度矢量满足矢量核姆霍兹方程Δ2E(r)+k2E(r)=0，同时遵守横场条件Δ·E(r)=0，在笛卡尔坐标系中，电场强度矢量可用(9)式表示为[10]

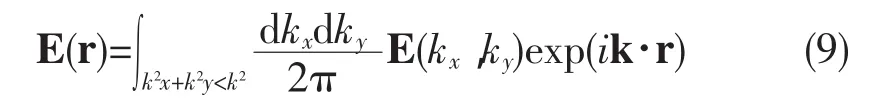
(9)式中忽略了随时间变化的位相因子exp(-iωt)，E(kx，ky)是光束电场矢量在波矢空间（或动量空间）的振幅矢量，即角谱。将(9)式代入(5)(6)和(7)式，考虑到，得光束的能量、动量、角动量的一般表达式为

按照横场条件，E(kx，ky)只能有两个相互正交的偏振态，用s和p表示这两个独立且相互正交的偏振态，可以将角谱 E(kx，ky)表示为 E(kx，ky)=Es+Ep=Ess+Epp，其中Es和Ep分别表示s偏振态和p偏振态的复振幅，相应地s和p是它们各自的单位矢量。令

s=sxex+syey+szez，

p=pxex+pyey+pzez，且 sj和 Pj(j=x，y，z)都是实数，因此，可将 E(kx，ky)表示为[10]

显然，横场条件并不能唯一确定矢量光束的偏振状态，存在着一个自由度，该自由度决定光束的矢量性质。不妨设sz=0，则

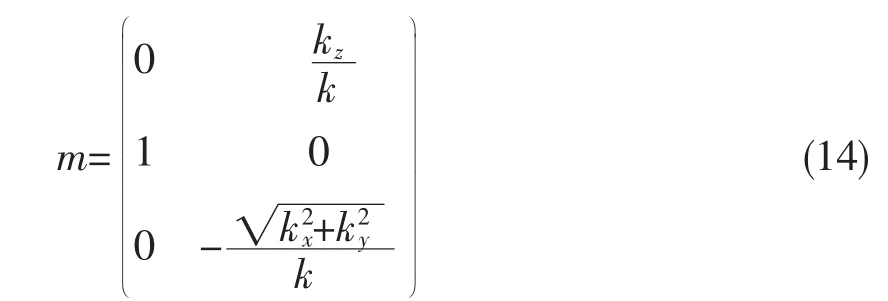
代入(13)式可得柱矢量光束的电场强度矢量为

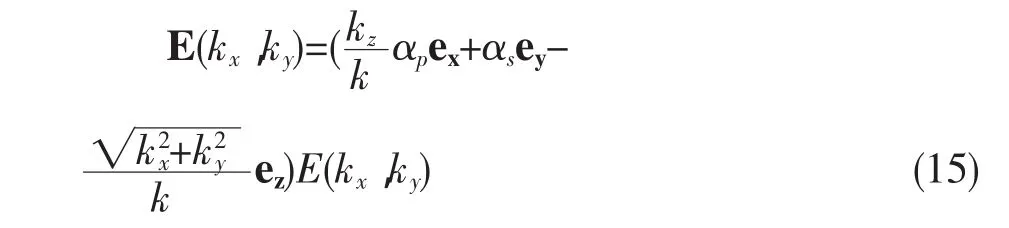
不难发现(15)式中所表示的光束的偏振情况具有轴对称性，以光轴（z轴）为对称轴，故称之为柱矢量光束[12]。由(10)式可得光束的能量为

由(12)式可得自旋角动量的z分量为

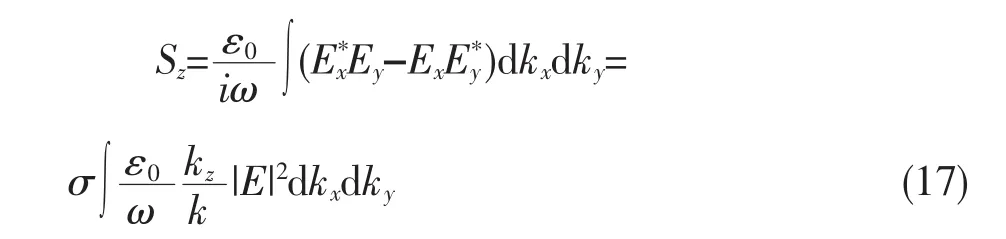
同理可得

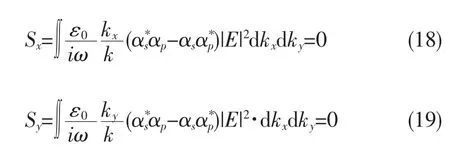
由(11)式得轨道角动量的z分量为

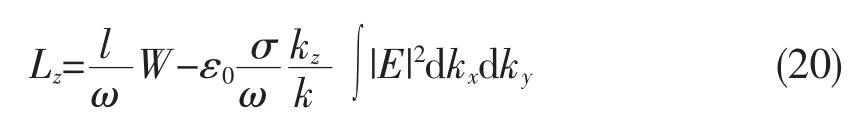
同理可得到

显然，由(17)(18)(19)式可知自旋角动量只有轴向分量，且轴向分量只与光束的偏振态(σ)和光束的结构（kz)有关；而由(20)(21)和(22)式可知轨道角动量也只有轴向分量，该分量与角向量子数(l)和偏振态(σ)都有关，同时与光束结构(kz)有关。在近轴近似情况下，kz≈k，此时，说明自旋角动量与能量的比值等于光束沿z轴方向的偏振度与角频率的比值，即光束中每个光子沿传播方向的自旋角动量取决于光束的偏振态，也就是光束的自旋量子数，σ=0，±1分别表示光束的线偏振态、左圆偏振态和右圆偏振态。而说明光束中每个光子沿传播方向的轨道角动量为(l-σ)h，与角向量子数和自旋量子数相关。因此，对于柱矢量光束，通常情况下无法将光束的角动量按传统的定义分为互不相干的自旋和轨道角动量两部分，即使在近轴近似情况下也是一样。

[1]Beth R A.Mechanical detection and measurement of the angular momentum of light[J].Phys Rev,1936,50:115.

[2]Allen L,Beijersbergen M W,Spreeuw R J C,et al.Orbital angular momentum of light and the transformention of Laguerre-Gaussian laser modes[J].Phys Rev A,1992,45:8185.

[3]Allen L,LembessisV E,B abikerM.Spin-or bit coupling in free-space laguerre-gaussian light beams[J].Phys Rev A,1996,53:R2937.

[4]Allen L,Padgett M J,Babiker M.The orbital angular momentum of light[J].Prog Opt,1999,39:291.

[5]Barnet S M,Allen L.Orbital angular momentum and nonparaxial light beams[J].Opt Commun,1994,110:670.

[6]Allen L,Padgett M J.The Poynting vector in Laguerre–Gaussian beams and the interpretation of their angular momentum density[J].Opt Commun,2000,184:67.

[7]O'Neil A T,Mac Vicar I,Allen L,et al.Intrinsic and extrinsic nature of the orbital angular momentum of a light beam[J].Phys Rev Lett,2002,88:053601.

[8]Marrucci L,Manzo C,Paparo D.Optical spin-to-orbital angular momentum conversion in inhomogeneous anisotropic media[J].Phys Rev Lett,2006,96:163905.

[9]Zhao Y,Edgar J S,Jeffries G D M,et al.Spin-to-orbital angular momentum conversion in a strongly focused optical beam[J].Phys Rev Lett,2007,99:073901.

[10]Li C F.Representation theory for vector electromagnetic beams[J].Phys Rev A,2008,78:063831.

[11]Li C F.Spin and orbital angular momentum of a class of nonparaxial light beams having a globally defined polarization[J].Phys Rev A,2009,80:063814.

[12]刘宝盈.柱矢量光束的自旋角动量[J].商洛学院学报,2010,24(4):11.