基于主成分分析法的渭河陕西段水环境质量评价
2013-11-19刘有军
吴 勇,刘有军,陈 伟,江 强
(云南省建筑科学研究院,云南昆明650223)
水环境质量评价就是通过一定的数理方法和其他手段,对水环境素质的优劣进行定量描述的过程。水环境质量评价必须以监测资料为基础,经过数理统计得出统计量 (特征数值)及环境的各种代表值,然后依据水环境质量评价方法及水环境质量分级分类标准进行环境质量评价。然而水环境系统是一个复杂的系统,在分析过程中,需要对多个变量进行分析,由于变量个数众多且彼此之间存在着一定的相关性,使得对主要信息的提取变得十分复杂。仅仅靠单一的指标来评价水环境质量的污染程度,难免产生片面性。因此对水环境质量进行综合评价的最大难点就是多目标性,即需要考虑众多表征水环境质量的指标。如何科学地、客观地将一个多指标问题综合成为少数几个指标问题成为水环境质量评价的研究重点。
近年来,随着多元统计分析的普及和应用,主成分分析法也成为一种新兴的评价方法,在环境质量综合评价方面应用广泛。主成分分析法能将高维空间的问题转化到低维空间去处理,使问题变得比较简单、直观,而且这些较少的综合指标之间互不相关,又能提供原有指标的绝大部分信息[1]。而且,伴随主成分分析的过程,将会自动生成各主成分的权重,这就在很大程度上抵制了在评价过程中人为因素的干扰。
1 环境现状
渭河在“品字泉”源头,其水质良好,清澈透亮,沁人心脾。从源头往下,进人水土流失区,河水由清变浊、由浊变浑。据有关资料介绍,在定西境内,河水含沙量达66.4kg/m3。渭河甘肃段有污染源87家,其中工业污染源62家,年接纳工业废水和生活污水2622万t。根据甘、陕环境保护部门的监测资料,渭河至陕西凤阁岭后,除个别指标超标外,其水质多年来均符合《地面水环境质量标准》Ⅲ类水标准,可以满足工农业用水的要求。
渭河陕西段有工业企业8000多家,呈串珠式分布于渭河及其支流两岸;尚有50多万个乡镇企业,其中乡镇工业企业达15万个左右。据对县及县以上工业企业的环境统计,渭河年接纳工业废水3.2亿t,城市生活污水1.69亿t;工业废水、生活污水处理率分别为77.9%、21%左右,绝大多数生活污水和22%的工业废水未经处理直接排入渭河水系。渭河水系年接纳重金属4.46t、有机污染物约10.75万t,其中COD达10.66万 t,约占有机污染物的99.2%。由于含重金属的工业废水已在20世纪80代基本治理达标,向渭河排放的重金属的数量较少,而渭河又是一条多泥沙、河槽宽阔、比降较小的河流,水流速度较慢、水层亦较浅,易于泥沙对重金属离子的吸附和沉降,河水中重金属的浓度较低,只有个别断面某种金属离子浓度超过地面水的Ⅲ类水的标准。渭河流经宝鸡、咸阳、西安和渭南等市,受到有机污染物的重复污染,已超出其稀释和自净能力,呈有机型污染特征,以氨氮、高锰酸盐指数、生化需氧量和挥发酚污染较为突出。
2 主成分分析法
2.1 方法简介
主成分分析法 (prineipalcoplllonentarialysis,PCA)也许是多变量分析中最古老和最著名的技术。最早是由美国统计学家皮尔逊 (PEARsoN)在1901年的生物学理论研究中引入的。是从多指标分析出发,运用统计分析原理与方法提取少数几个彼此不相关的综合性指标而保持其原指标所提供的大量信息的一种统计方法。1933年,HOTELLING[2]将此想法应用于心理学研究,并得到了进一步的发展。1947年,KARHuNEN[3]独立地用概率论的形式再次将其研究,其后LOEVE将该理论进一步扩充和完善,故PCA理论也称为KAHRUNENLOEVE变换。
2.2 基本原理
主成分分析法的工作对象是样本点x定量变量类型的数据表。它的工作目标,就是要对这种多变量的平面数据表进行最佳综合简化。也就是说,要在力保数据信息丢失最少的原则下,对高维变量进行降维处理[4]。
除了降低多变量数据系统的维度以外,主成分分析同时还简化了变量系统的统计数字特征。对于任意p个变量,描述它们自身及相互关系的数字特征包括均值、方差、协方差等,一共有P+(1/2)p(P+l)个参数。经过主成分分析后,每个新变量系统的数字特征减少了P+(1/2)p(p-1)个。假定有n个水体样本,每个样本共有p个指标变量,则构成了一个n×p阶的地理数据矩阵

利用p个原始变量构成少量几个新的综合变量,使得新变量为原始变量的线性组合,记原来的变量指标为x1,x2,…,xP,z1,z2,…,zm(m≤p)为新变量指标,则:

z1,z2,…,zm分别称为原变量指标 x1,x2,…,xP的第一,第二,…,第m主成分,在实际问题的分析中,常挑选前几个最大的主成分。①zi与zj(i≠j;i,j=1,2,…,m)相互无关;②z1是x1,x2,…,xP的一切线性组合中方差最大者,z2是与z1不相关的x1,x2,…,xP的所有线性组合中方差最大者;……;zm是与 z1,z2,……,zm-1都不相关的x1,x2,…,xP的所有线性组合中方差最大者。
3 数据的收集、处理及分析
3.1 MATLAB数据处理软件
MTLAB是美国Math Works公司出品的商业数学软件,用于算法开发、数据可视化、数据分析以及数值计算的高级技术计算语言和交互式环境,主要包括MATLAB和Simulink两大部分。本次采用MATLAB数据处理软件主要是进行高级矩阵和阵列语言的计算。
3.2 数据收集
本次对渭河干流陕西段共选取了8个断面,分别为咸阳铁桥S1、草滩桥S2、耿镇桥S3、新丰桥S4、黑河入渭S5、涝河入渭S6、新河入渭S7、临河入渭S8共8个断面进行检测,评价选用溶解氧、生化需氧量、高锰指数、氨氮、挥发酚、氰化物、汞、六价铬8个评价参数,表1为检测数据。
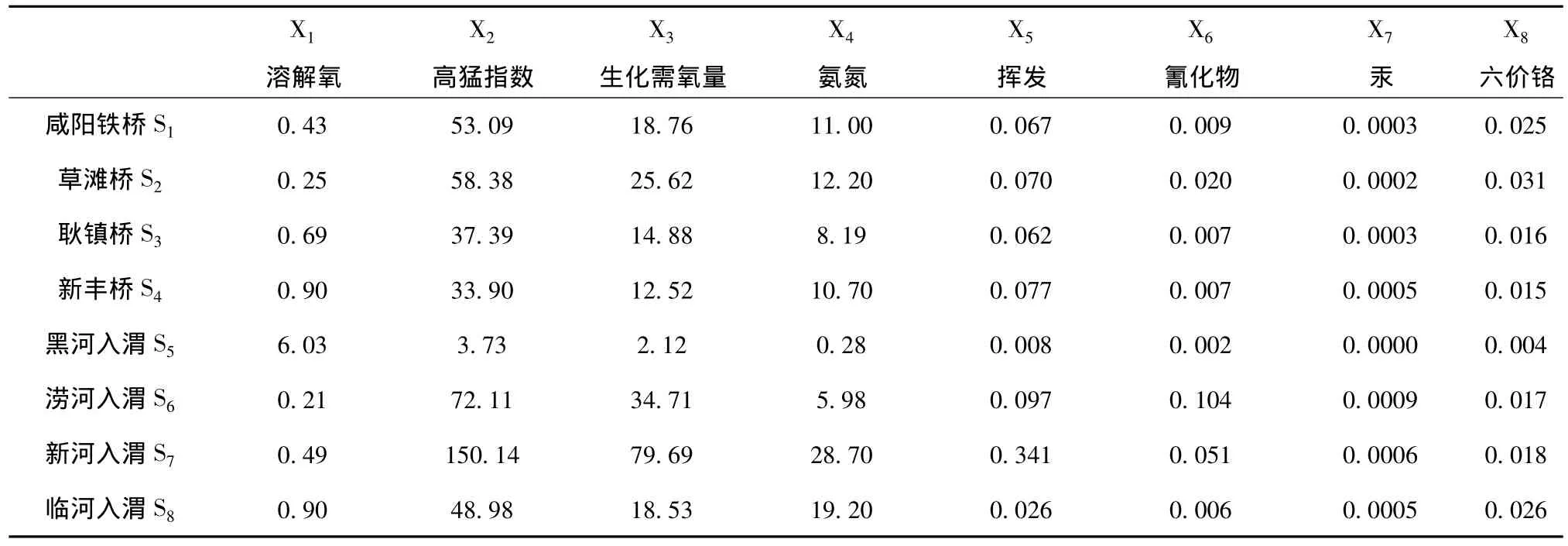
表1 渭河8个断面检测结果表

表2 检测数据标准化处理后的结果
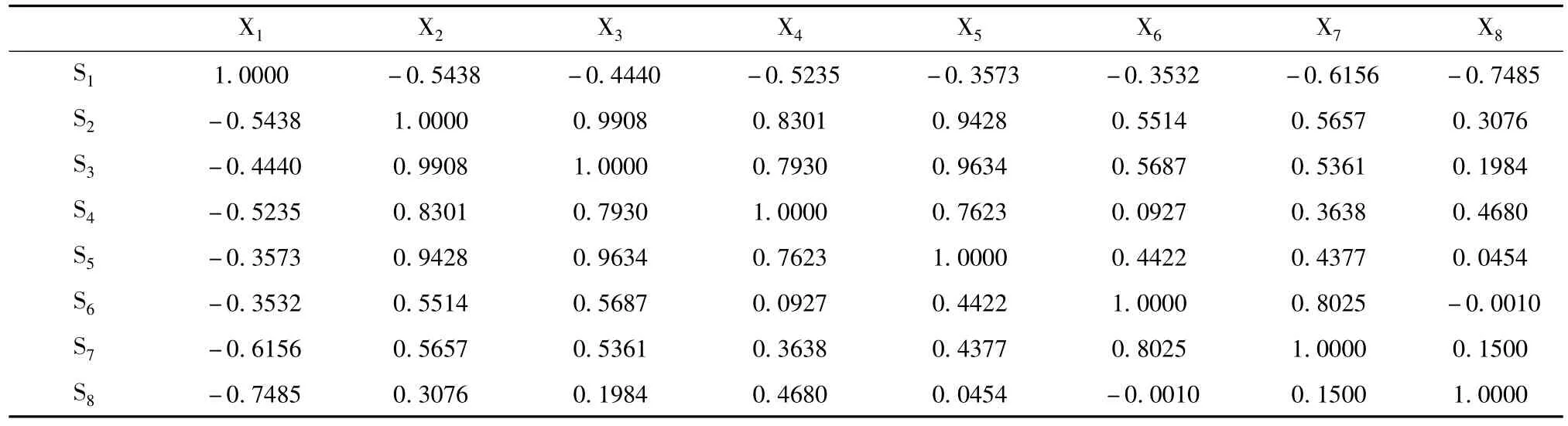
表3 检测指标相关系数矩阵
3.3 数据计算及结果
对同一变量减去其均值再除以标准差得到的新数据为标准化后的数据。对于特殊评价参数溶解氧,首先对其进行导数处理,然后再进行标准化处理,表2为检测结果标准化后的数据。根据标准化数据计算相关数矩阵,检测指标相关系数矩阵如表3所示。
再由相关系数矩阵计算特征值,以及各个主成分的贡献率与累计贡献率,特征值、特征向量的计算是根据MATLAB软件结合计算而来。计算数据见表4、5、6,由此可知,第一,第二,第三主成分的累计贡献率已高达86.5%,故只需求出第一、第二、第三主成分z1,z2,z3即可。
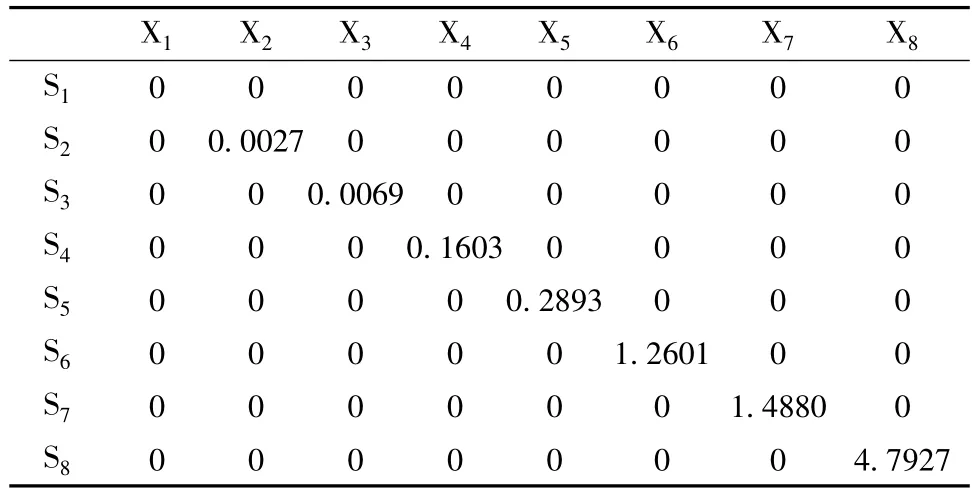
表4 特征值
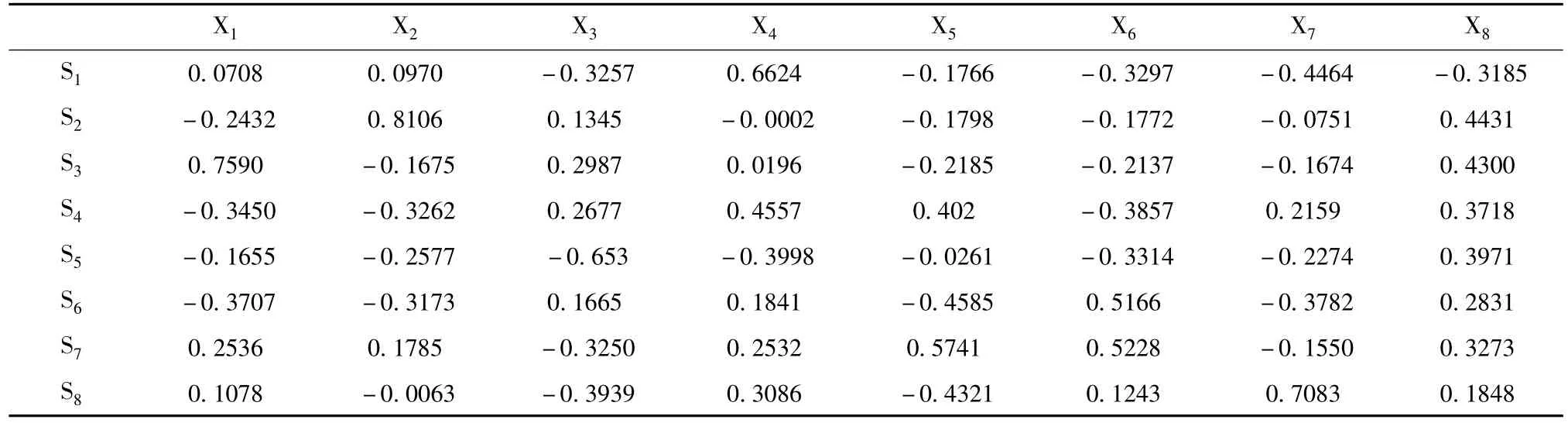
表5 特征向量表格

表6 特征值和累计贡献率
根据主成分载荷公式计算主成分载荷,根据特征值 λ1=4.7927,λ2=1.4880,λ3=1.2601分别求出其特征向量e1,e2,e3,再用公式(i,j=1,2,3,…,p),计算各变量在主成分1,2,3上的载荷。

表7 检测指标载荷矩阵
从表3的相关矩阵出发,计算各主成分的特征值、方差贡献率及累积方差贡献率和各监测指标的载荷矩阵,结果见表6和表7。由表7中相关系数阵的特征值可以看出,前3个主成分已满足≥85%的条件,因此只需用3个主成分取代原有8个指标,就能很好地表达。由表7监测指标的载荷矩阵计算前3个主成分的表达方式:

将各监测断面的标准化数据代入所提取的3个主成分公式中,得到各断面的主成分,再根据Prin1、Prin2、Prin3和对应的客观权重 e1、e2、e3(方差贡献率)的积之和计算得出各监测断面的综合主成分Prin1~3,监测断面的主成分计算结果如表8所示。根据《地面水环境质量标准》(GB3838-2002),和《地表水资源质量标准》(SL63-94)可得水质分级标准,如表9所示。
根据表8的各个监测断面综合主成分,参考综合主成分分级标准表8得到各个断面的水质类别:黑河入渭 (S5)水质属于Ⅰ类;耿镇桥 (S3)水质属于Ⅲ类;咸阳铁桥 (S1)、新丰桥 (S4)水质属于Ⅳ类;草滩桥 (S2)、涝河入渭 (S6)、新河入渭 (S7)以及临河入渭 (S8)水质属于Ⅴ类。由此可见,黑河入渭 (S5)水质最好,其他断面的水质均受到不同程度的污染,渭河陕西段水体综合水质为Ⅴ类,污染很严重,不能满足此区域河流水体的功能要求。
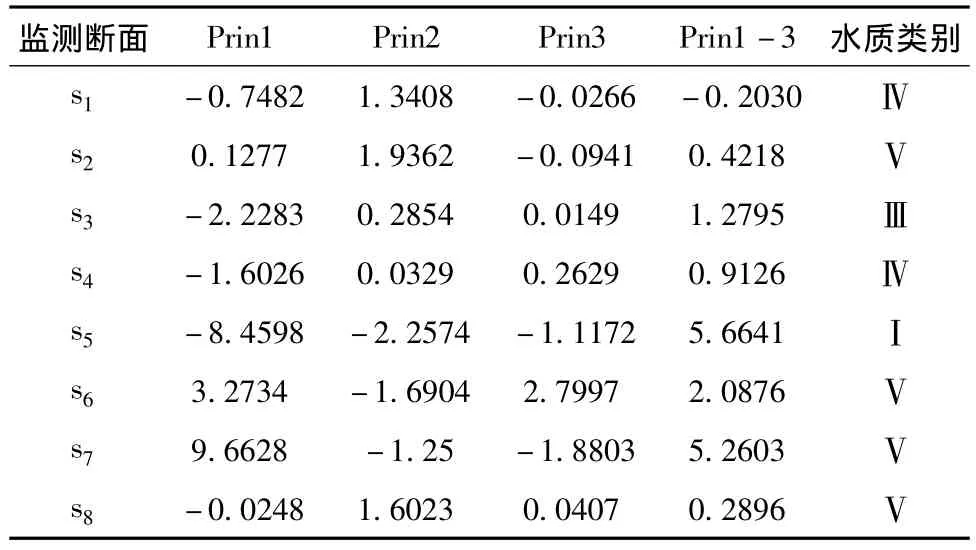
表8 各监测断面的主成分
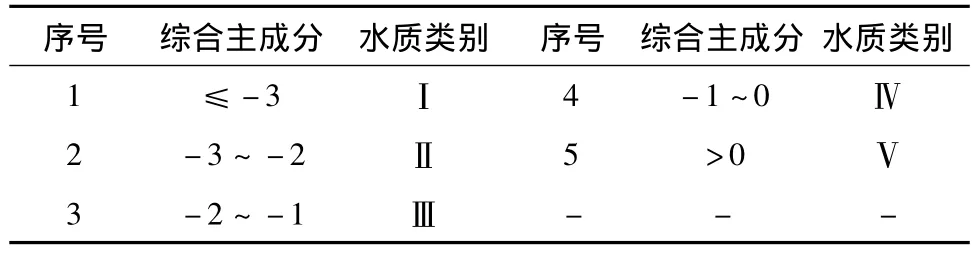
表9 水质分级标准
3.4 结果原因分析
(1)造纸企业数量多、规模小、分布广。2007年不完全统计全省共有造纸企业850多家,平均规模为400 t/a,可见CODMn污染指数较高主要是造纸企业引起的。
(2)化肥和农药使用不合理。宝鸡市土壤养分失衡问题一直比较突出,由于大量使用廉价劣质的氮肥和农药,以及氮、磷、钾肥施用不成比例,因此使氮肥溶解而被冲入水体中造成污染。
(3)河道生态水量不足。渭河宝鸡峡林家村引渭工程近310年年平均取水量为4.83亿m3,占河道水量的49.07%,造成河道生态水量大幅下降、水体污染物浓度得不到稀释,这也是现今污染指数居高不下的重要原因。
4 结论
(1)主成分分析法具有较好的精确度,其可以通过细化的计算数值反应,能有效地用于水环境质量评价中;MATLAB数据处理软件是现今运用较广泛的数据处理系统。
(2)渭河陕西段水体综合水质为Ⅴ类,污染很严重,不能满足此区域河流水体的功能要求。
(3)渭河陕西段水的污染主要是由造纸企业污水排放、化肥和农药使用不合理及河道生态水量不足引起的。
[1]王晓鹏.河流水质综合评价之主成分分析法[J].数理统计与管理,2001,20(4):49-52.
[2]HotellingH.Analysis of a eomplex of statistieal variables into prineipal component[J].Journal of Edueational Psyehology,1933,(24):417-441,498-520.
[3]KarhunenK.Uber 1ineare methoden in der washrseheinliehkeitsreehnung [J].AnIer Aeard Sei,Fennieade Ser A l,1947,37:3 -79.
[4]任若恩,王惠文.多元统计数据与分析——理论、方法、实例[M].北京:国防工业出版社,1999.
