考虑应力拱效应的隧道荷载-结构模型

尹蓉蓉

(1.同济大学 地下建筑与工程系,上海 200092)(2.江苏科技大学 船舶与海洋工程学院,江苏 镇江 212003)

目前所采用的隧道结构设计模型包括经验类比模型、荷载-结构模型和地层-结构模型.荷载-结构法与地层-结构法对隧道荷载的认识不同,前者认为作用在隧道上的是围岩的松散荷载,后者认为隧道承担由地层变形产生的变形压力.隧道计算理论中,隧道荷载的确定与结构的计算方法是其重要部分.由于荷载-结构法概念清楚、方法简明,容易接受和掌握,因此是目前最为常用的一种地下结构计算方法[1-2].地层-结构法又称为连续介质模型,将围岩看作地下结构的一部分,地下结构的作用是在洞室周围围岩开挖引起应力重分布的过程中参与围岩的变形,起到了约束和限制围岩的作用,与围岩组成共同的受力整体,这种计算方法比较符合喷锚支护的受力特点.

根据荷载-结构法的计算原理可知,围岩弹性反力的假定对计算结果影响最大.因此,用荷载-结构法对隧道进行计算时,重点是提出一个相对合理的弹性反力的假定以确定合适的计算模型.文中的主要工作是以地层-结构法为参照，建立考虑应力拱效应的隧道荷载-结构模型,使该模型的计算结果更符合隧道实际受力状态.

1 考虑应力拱效应的荷载-结构模型

1.1 建立考虑应力拱效应荷载-结构计算模型的必要性

对于荷载-结构法,根据地层对结构变形的约束能力,又分为“径向和切向反力法”、“自由变形法”、“三角形反力法”和“径向反力法”4种计算模型[3].其中,“径向反力法”在实际工程中应用较广,该模型通常在隧道衬砌全周设置径向压弹簧或在拱顶处不设置弹簧其他部位设置径向压弹簧.

实践证明,运用“径向反力法”计算所得隧道衬砌的内力与变形比实际承受的内力和变形大,使得衬砌设计尺寸趋于保守.造成这种情况的主要原因是:①计算时,没有考虑围岩的自承作用而使得作用在衬砌上的荷载比衬砌实际承受的荷载大;②在实际隧道工程中,隧道拱顶处由于受到围岩压力的作用会产生向下的变形,拱顶处的围岩压力向侧墙传递,导致拱顶处衬砌所承受的围岩压力变小,侧墙处衬砌所承受的围岩压力变大,最终在隧道拱顶范围内会形成应力拱效应;③在《公路隧道设计规范》(JTGD70-2004)中指出:“弹性抗力、粘结力均属围岩对衬砌的约束力,鉴于迄今对粘结力作用的研究不多,故通常仅按弹性抗力计算,而将粘结力对衬砌结构的有利作用视为安全储备.”因此,计算中通常不考虑围岩和衬砌之间的粘结力.

传统的荷载-结构计算模型不能很好地模拟围岩与衬砌之间的相互作用,为了安全起见,设计中,衬砌之上的荷载取得偏大,计算所得衬砌结构的内力和变形要比实际值大很多,这样设计出的衬砌厚度要比实际满足安全需要的衬砌厚度大很多,相应的工程造价就高,从而造成不必要的浪费.

1.2 考虑应力拱效应的荷载-结构模型的概念

实际隧道工程中,隧道拱顶处衬砌由于受到围岩压力的作用会产生向下的变形,拱顶处的围岩压力变小,同时向侧墙传递,这就导致拱顶处衬砌受力减小,侧墙处衬砌受力增加,这一现象与拱桥等拱形结构中存在的压力拱现象类似,因此,将这种由于拱顶衬砌变形而导致力的传递的现象定义为应力拱效应(图1).

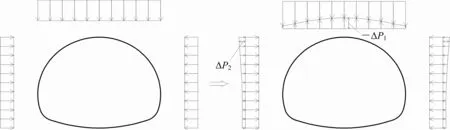
图1 应力拱效应示意图Fig.1 Diagram of stress arching effect

根据实际工程中隧道衬砌之上的荷载特点,将以地层-结构法计算所得隧道衬砌受力、变形的结果为参照,建立一种新的荷载-结构法计算模型,该模型区别于以往比较常见的在隧道衬砌全周设置径向压弹簧或在拱顶处不设置弹簧其它部位设置径向压弹簧这两种情况,而在拱顶某一范围设置拉弹簧模拟围岩对衬砌变形的限制以及围岩与衬砌之间的粘结作用,其余部位设置压弹簧,以期望新的荷载-结构模型计算所得隧道衬砌受力、变形更符合实际隧道衬砌的受力、变形情况.特别需要指出的是,文中仅考虑拱顶处存在松动土压力的情况,不考虑隧道受偏压松动土压力不处于拱顶的情况.

2 几种模型的比较

由于荷载-结构法与地层-结构法对隧道荷载的认识不同,从而导致两种计算方法对隧道衬砌的受力分析结果有很大差别,文中选择某单拱标准二车道隧道作为研究对象,以文献[4]的试验研究内容为依托,比较地层-结构法、全周设置压弹簧、拱顶处不设置弹簧其余部位设置压弹簧，以及拱顶处设置拉弹簧其余部位设置压弹簧荷载-结构法这4种模型的计算结果.

2.1 算例概况

1) 试验情况

文献[4]所采用的二车道隧道断面如图2,隧道内轮廓为三心圆,净宽11 m,净高8.77 m.试验中模型材料的力学性能如表1.

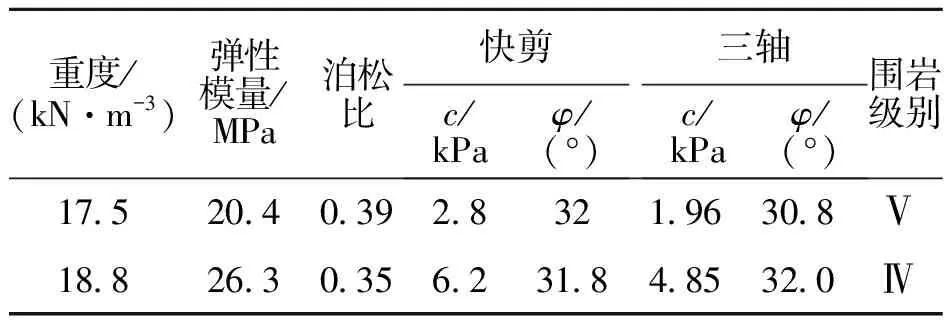
表1 模型材料力学性能Table1 Mechanical performance of model materials

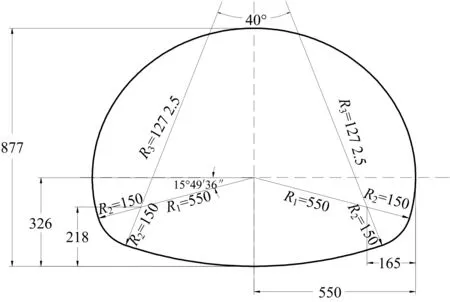
图2 二车道隧道断面图(单位:cm)Fig.2 Section diagram of hingway tunnel with two lanes (unit: cm)

2) 确定围岩压力

从表1中可以看到,试验所得模型材料的参数基本上处于规范给出的Ⅳ，Ⅴ级围岩材料参数范围之内.根据试验结果可以计算出:对于Ⅳ级围岩中埋深为30 m隧道,垂直均布压力q=76.1 kN/m2,按照《公路隧道设计规范》[5]可以判断出该隧道属于深埋隧道,因此,水平均布压力e=19.04 kN/m2;对于Ⅴ级围岩埋深为10 m隧道,垂直均布压力q=175 kN/m2(埋深乘以围岩重度),按照《公路隧道设计规范》[5]可以判断出该隧道属于浅埋隧道,因此,水平均布压力e=30.2 kN/m2.

3)模型参数

隧道模型参数见表2.

表2 隧道模型参数Table2 Tunnel model parameters

2.2 计算模型

1) 地层-结构法计算模型

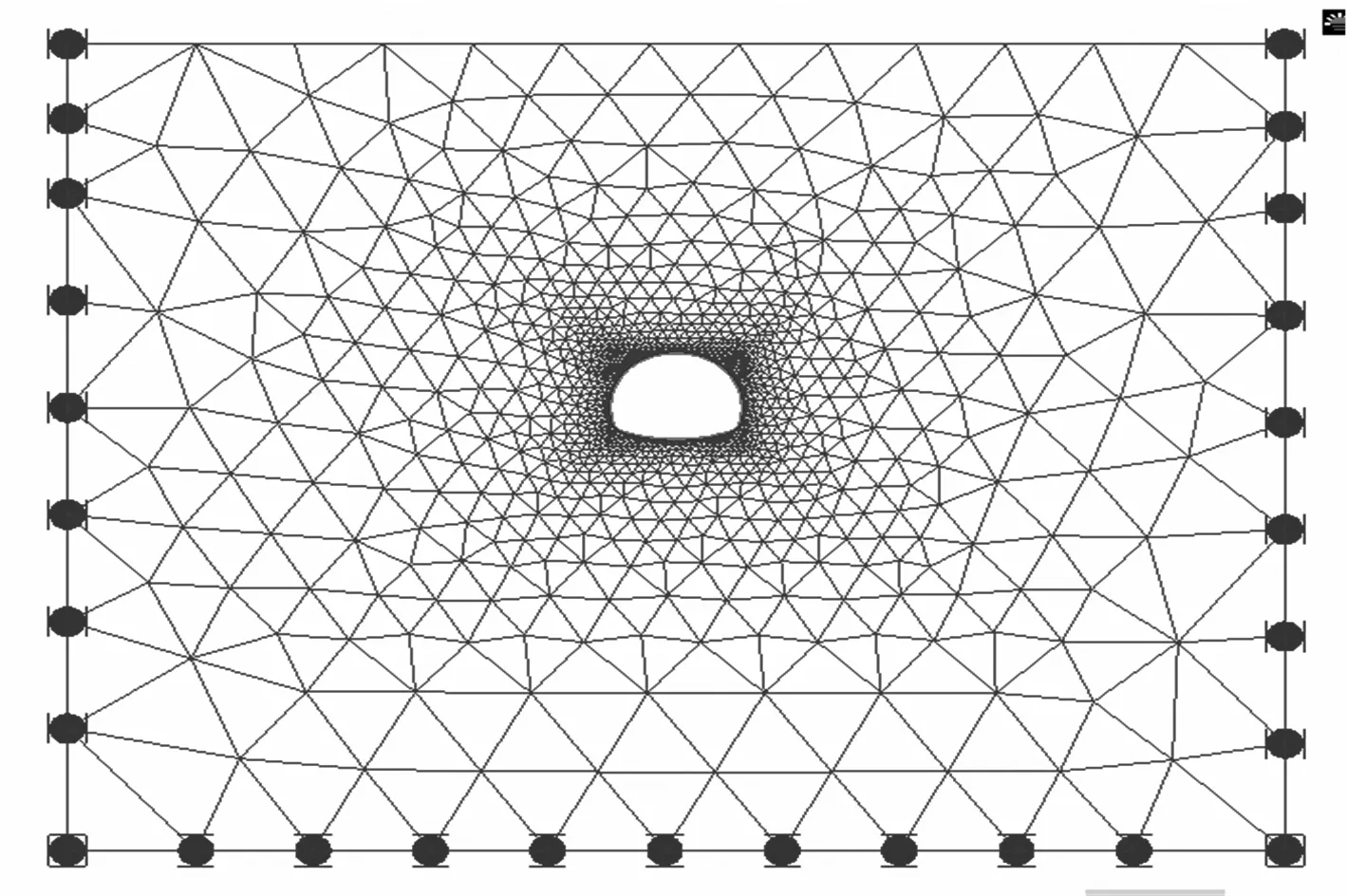
利用同济曙光有限元软件分别对深埋、浅埋隧道建立包含施工过程的地层-结构计算模型,计算模型如图3.采用地层结构法计算时,可通过对释放荷载设置释放系数控制初期支护的受力,以使初期支护和二次衬砌能按较为合理地分担比例共同承受释放荷载的作用.本算例开挖工程中释放的荷载比例为60%,由衬砌承担的荷载比例为40%.

2)荷载-结构法计算模型

利用同济曙光有限元软件建立深埋、浅埋两种隧道荷载-结构模型,模型采用全周设置压弹簧、全周设置径向压弹簧以及拱顶不设置压弹簧而其余部位设置压弹簧3种形式,初衬和二衬采用梁单元离散,接触面采用接触面单元离散,模型衬砌结构共划分为486个单元,其中包括初衬单元162个,二衬单元162个,接触面单元162个,计算简图如图4,作用于衬砌的荷载按松散荷载计算,水平荷载向右为正,竖向荷载向上为正,这几种计算模型中弹簧的设置方式不同.

a)深埋

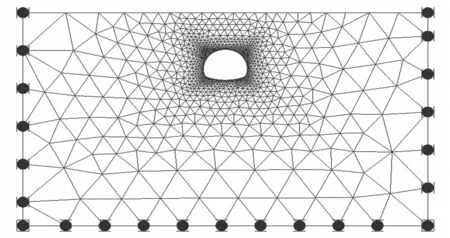
b)浅埋

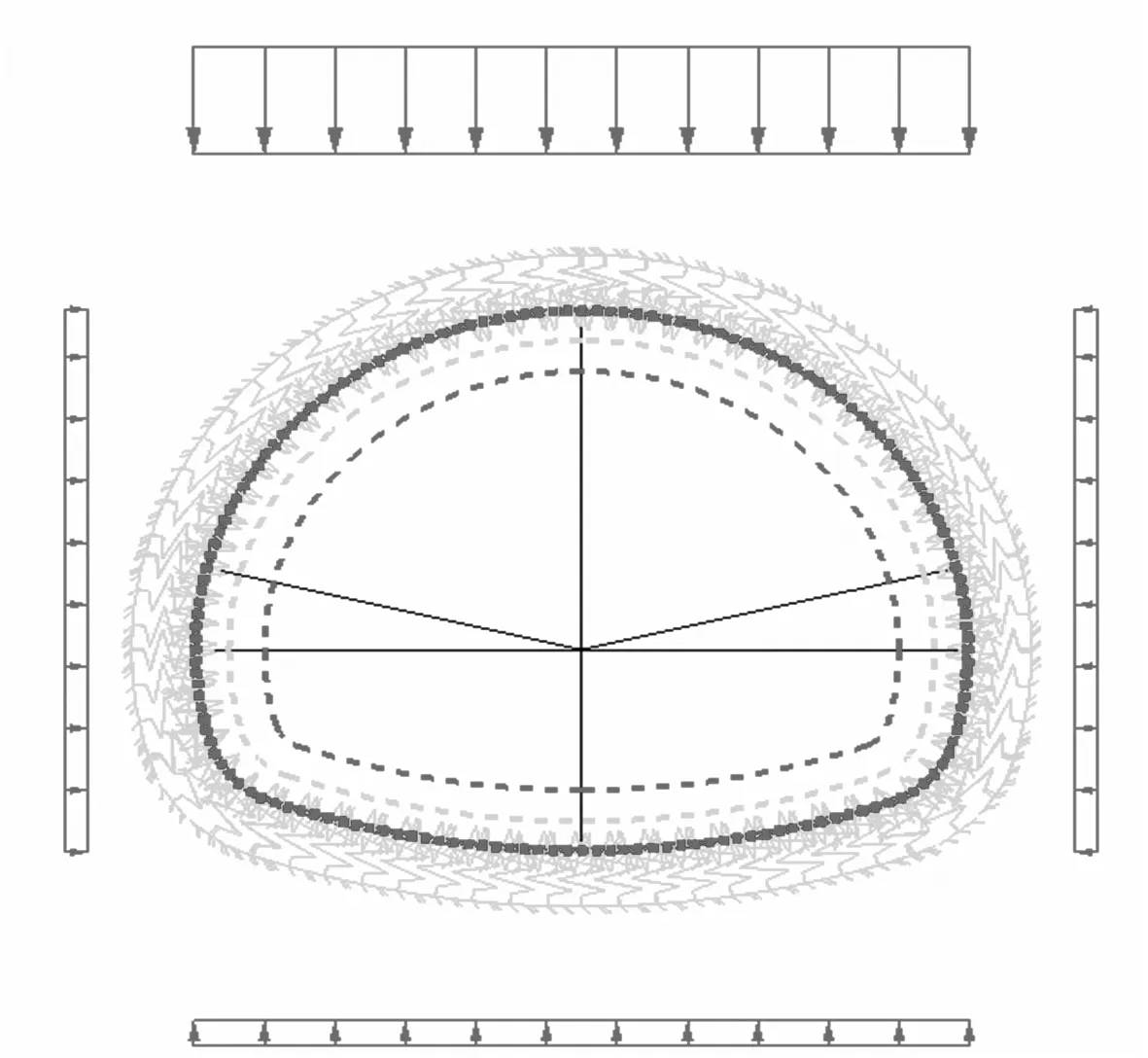
a) 深埋

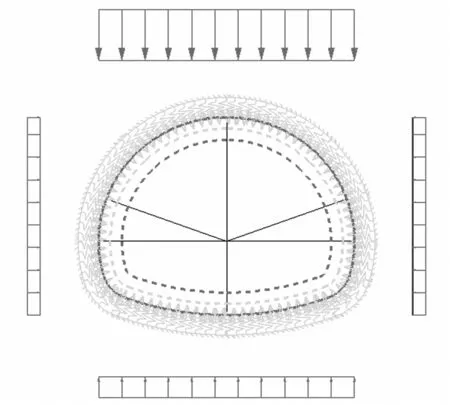
b) 浅埋

2.3 计算结果

用荷载-结构模型与地层-结构模型对深埋、浅埋隧道进行计算,结果分别见图5,6.用地层-结构法计算围岩压力准确性取决于围岩参数选取得是否准确,文中在用地层-结构法对深埋隧道建模时,围岩参数根据文献[4]的试验结果进行取值的,因此,图5a)，图6a)所示的隧道衬砌弯矩应该符合衬砌实际的受力情况,可以用这一弯矩值作为对比依据.

从图5,6可以看出,无论是深埋隧道还是浅埋隧道,用全周设置压弹簧或拱顶不设置弹簧而其余部位设置压弹簧的荷载-结构法模型计算所得衬砌的弯矩图在数值和变化趋势上与地层-结构法差别较大,尤其是在拱顶和边墙位置.图5b),c)和图6b),c)中隧道衬砌在起拱线以上的弯矩都比图5a)和图6a)中的弯矩值要大,而且大很多,这除了是因为用荷载-结构法模型计算时将围岩压力全部作用在衬砌上,没有考虑围岩的自承作用以及围岩与衬砌之间的粘结作用外,很重要的一点是没有考虑隧道拱顶处的应力拱效应.图5b),c)和图6b),c)中隧道衬砌在拱顶处的弯矩值很大,而图5d)和图6d)中隧道衬砌在拱顶处的弯矩值减小了很多,这主要是由于拱顶处拉弹簧的拉力作用模拟了隧道拱顶处衬砌由于变形而传递给围岩的那部分围岩压力.

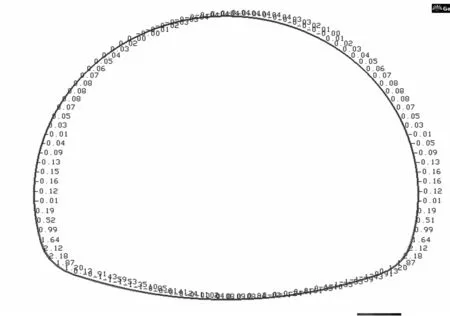
a)地层-结构法

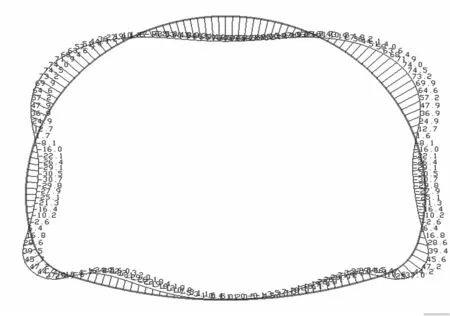
c) 拱顶不设置弹簧

d) 拉压弹簧弹性抗力系数比例1∶2

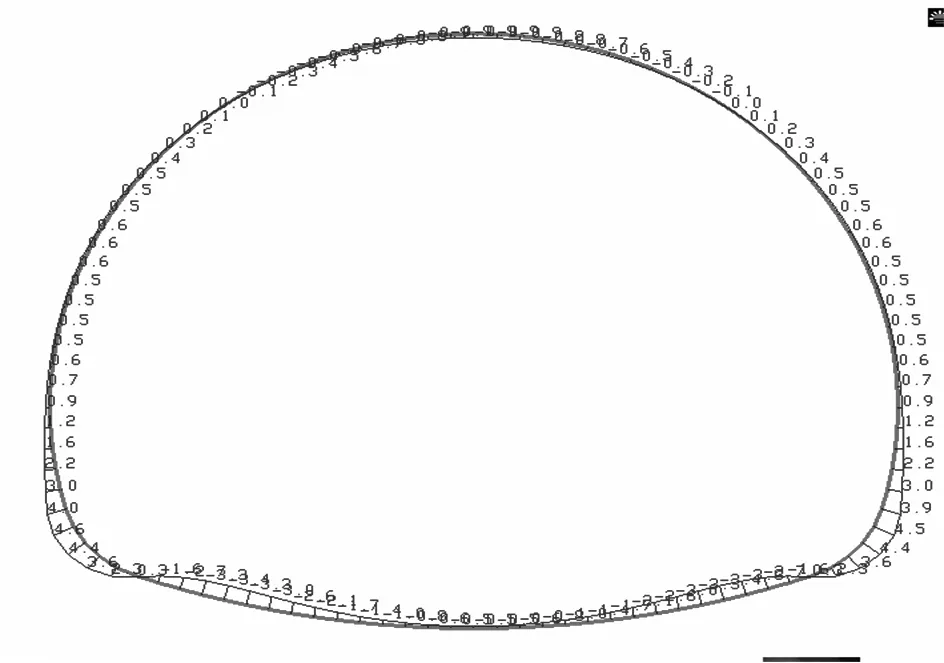
a)地层-结构法

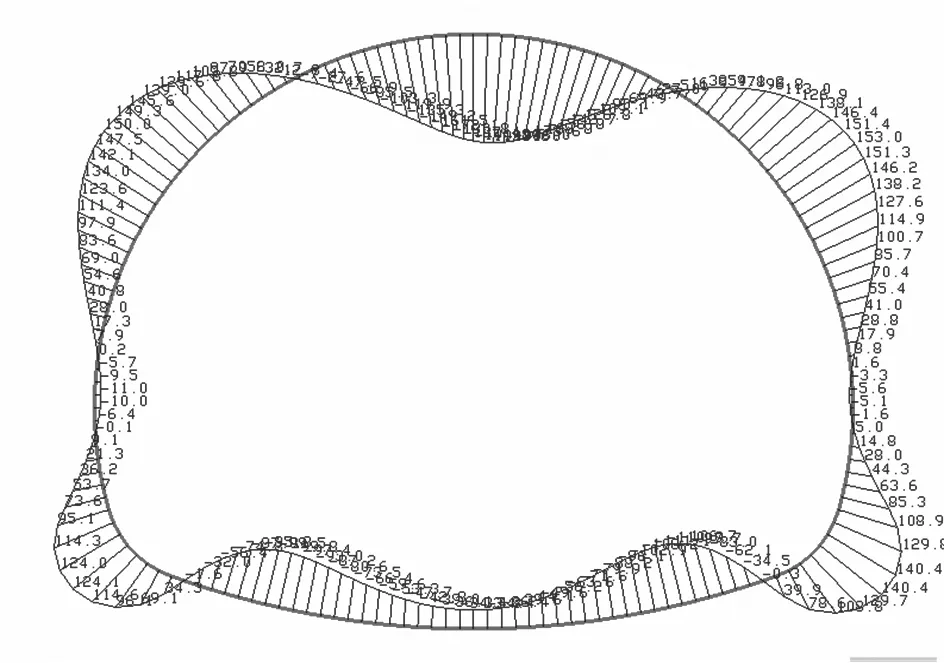
b) 全周设置压弹簧

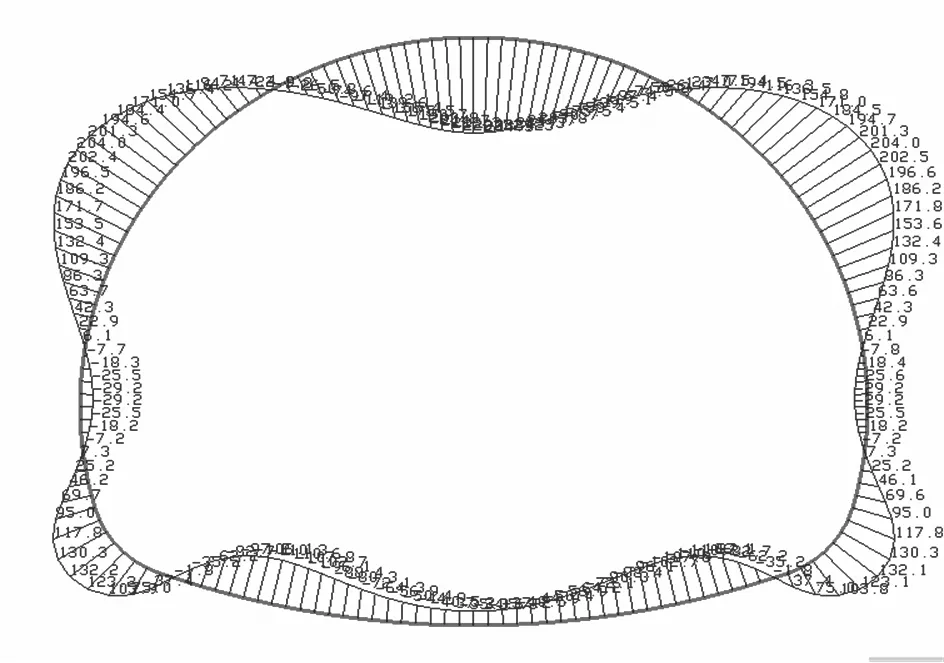
c) 拱顶不设置弹簧

d) 拉压弹簧弹性抗力系数比例1∶2

3 考虑应力拱效应的荷载-结构模型计算研究

从前面的计算可以看出,考虑应力拱效应的荷载-结构模型计算所得衬砌的弯矩在数值和变化趋势上与地层-结构法更接近,但是拉弹簧的设置范围以及弹性抗力系数的大小需通过计算确定.图7为模型流程图

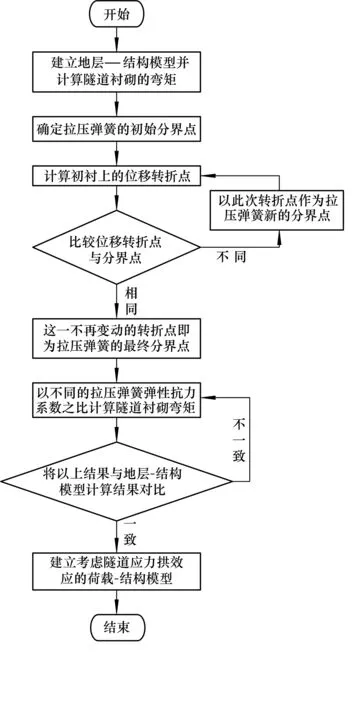
图7 考虑应力拱效应的荷载-结构法计算模型流程Fig.7 Flow chart of load-structure method calculation model considered the stress arching effect.

3.1 拉压弹簧分界点的位置

要在拱顶部位设置拉弹簧,其余位置设置压弹簧,首先要确定拉压弹簧分界点的位置,

文中通过手工迭代确定拉压弹簧分界点的具体位置,即图8中A，B两点的位置.A，B两点位于隧道衬砌4上,拱顶的圆弧中心O与A，B两点连线的夹角α所围成的隧道衬砌部分是拱顶范围.迭代过程如下:第1次迭代是用传统的隧道衬砌全周设置均布压弹簧的模型计算得到衬砌上的位移,由于弹性反力是作用在隧道衬砌上的,因此,根据计算结果可以得到拱顶处衬砌产生向洞内的位移,边墙处衬砌产生向围岩方向的位移,那么在拱顶与边墙之间必然存在某个点,在该点处衬砌位移为零,这一点即为衬砌位移的转折点,设定为初始分界点,即图8中点A0和B0；第2次迭代是以初始分界点A0和B0为界,在隧道衬砌的拱顶部位设置拉弹簧，其余部位设置压弹簧建立模型进行计算,获得新的位移转折点,即图8中点A1和B1；第3次迭代是以第2次迭代得到的位移转折点A1和B1作为新的分界点,拱顶部位设置拉弹簧其余部位设置压弹簧建立模型进行计算.依此类推,通过手工迭代,直到此次迭代得到的衬砌上的位移转折点与前一次迭代确定的分界点的位置相同为止,这一不再变动的转折点的位置即为拉压弹簧最终的分界点,即图8中点A和B,则此次迭代也是最终一次迭代.

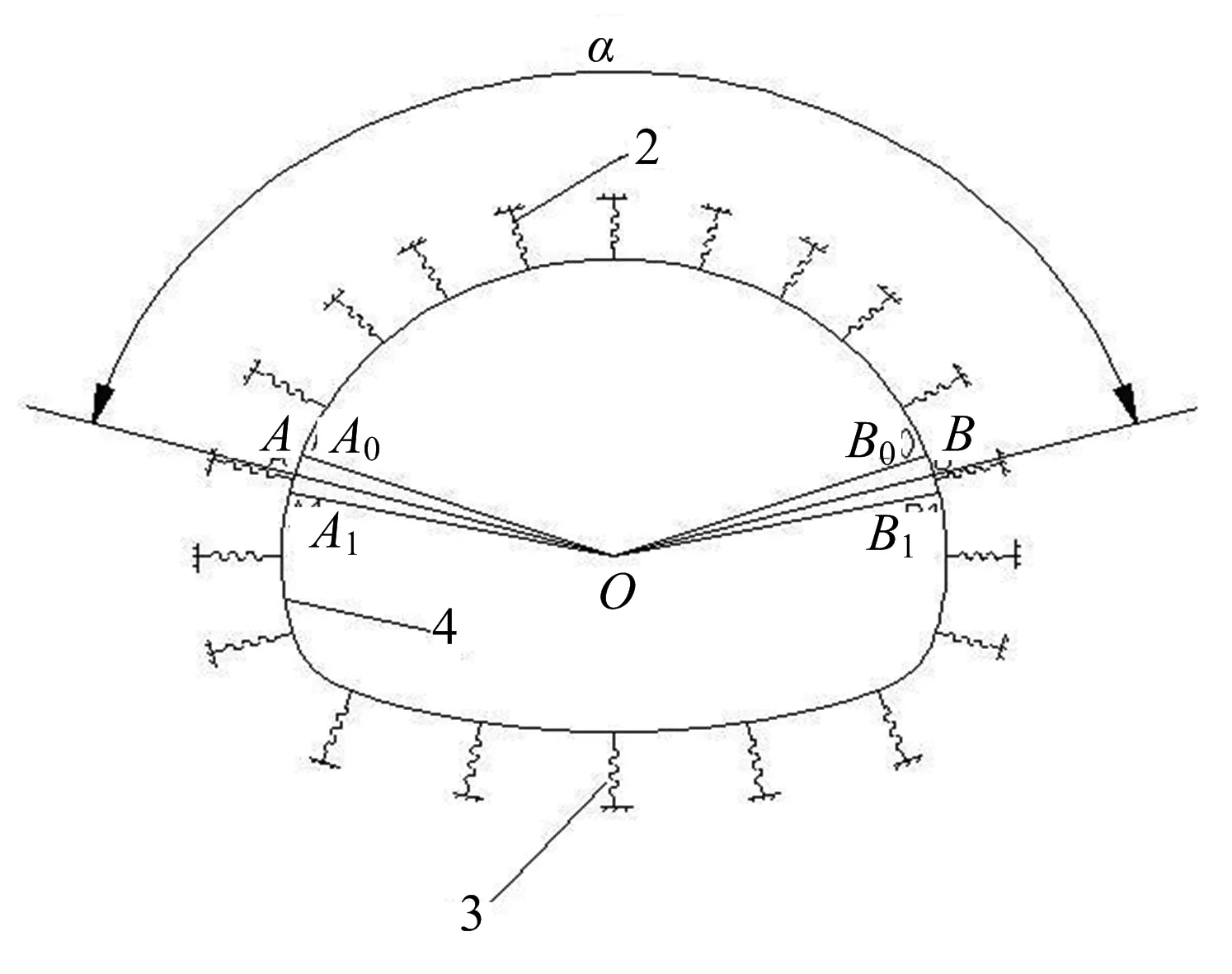
图8 考虑隧道应力拱效应的荷载-结构模型Fig.8 Diagram of load-structure model considered the tunnel stress arching effect

表3，4分别给出了深埋和浅埋隧道不同的拉弹簧与压弹簧弹性抗力系数之比时拉压弹簧分界点处于拱顶周围的位置.

3.2 拉弹簧弹性抗力系数的确定

拉压弹簧的弹性抗力系数之间合理的比例关系可以通过试算确定,根据这一比例关系建立的荷载-结构模型计算所得结果将会接近隧道衬砌实际受力情况,并且与用地层-结构模型的计算结果趋于一致.通过试算几个典型的拉弹簧弹性抗力系数与压弹簧弹性抗力系数之间的比例关系建立的荷载-结构模型计算得到的深埋、浅埋隧道衬砌的弯矩见图9，10,图9分别给出了以拉弹簧与压弹簧的弹性抗力系数之间比例关系为3∶1，2∶1，1∶1，3∶4，2∶3，1∶2，1∶3，1∶4时计算得到深埋隧道衬砌的弯矩图.图10分别给出了以拉弹簧与压弹簧的弹性抗力系数之间比例关系为3∶1，2∶1，1∶1，2∶3，1∶2，1∶3，1∶4时计算得到浅埋隧道衬砌的弯矩图.

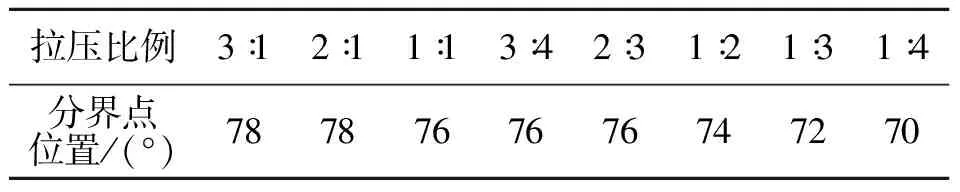
表3 深埋隧道拉压弹簧分界点的位置Table.3 Position of division point of tensile spring and compressional spring of deep tunnel

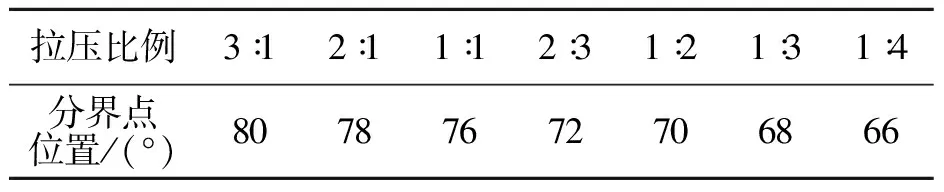
表4 浅埋隧道拉压弹簧分界点的位置Table4 Position of division point of tensile spring and compressional spring of shallow tunnel

a)3∶1

b)2∶1

c)1∶1

d) 3∶4

e) 2∶3

f) 1∶2

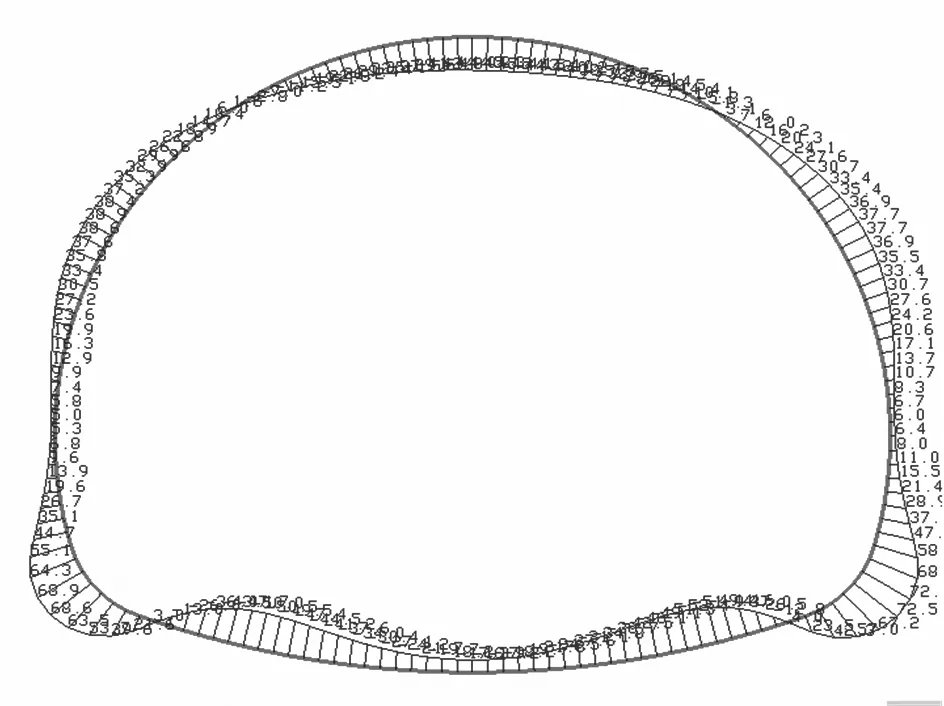
h) 1∶4

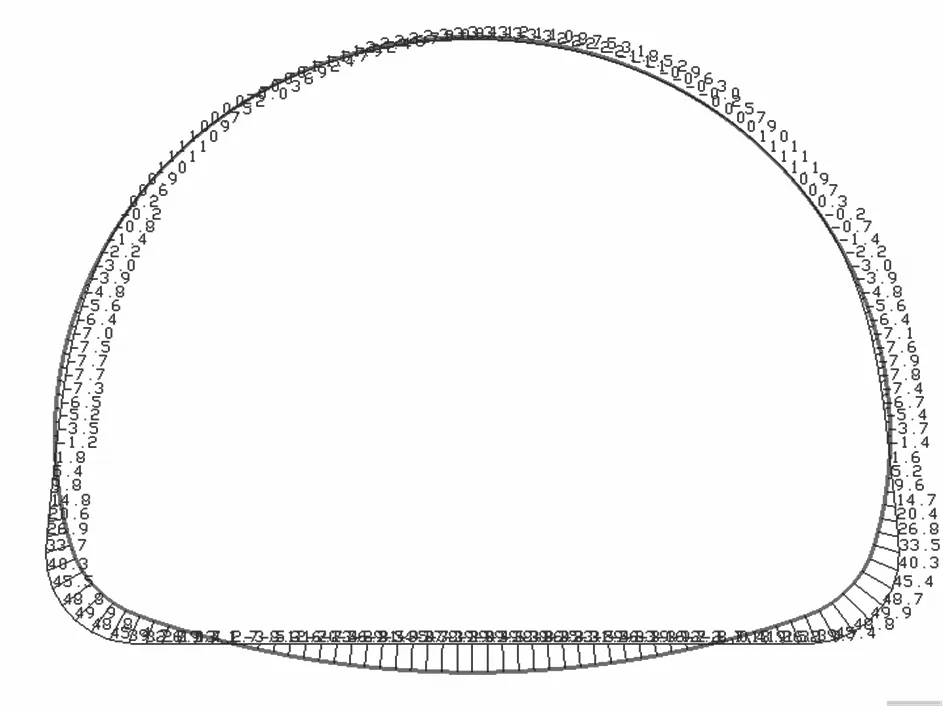
a) 3∶1

b) 2∶1

c) 1∶1

d) 2∶3

e) 1∶2

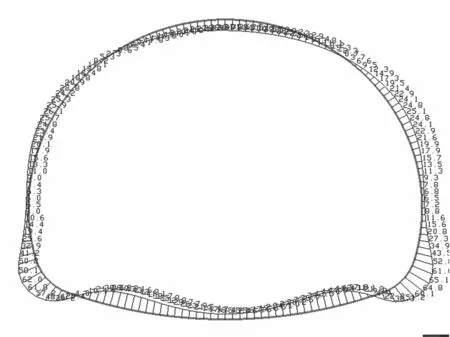
f) 1∶3

g) 1∶4

4 结论

根据计算结果,可以得出如下结论:

1)从图9,10中可以看出,无论是深埋隧道还是浅埋隧道,与传统的荷载-结构法模型相比,考虑应力拱效应的荷载-结构模型中拉弹簧的设置范围内隧道衬砌受力改变比较明显,在压弹簧范围内,离拉弹簧越远处隧道衬砌受力的改变越小,起拱线附近衬砌受力的改变较小,远离拉弹簧区域的隧道底部衬砌受力几乎不受影响;

2)根据用拉压弹簧荷载-结构模型对深埋隧道衬砌弯矩计算结果(图9)可以看出,拉弹簧弹性抗力系数与压弹簧弹性抗力系数之比在1/2～2之间时,考虑应力拱效应的荷载-结构计算模型对隧道衬砌弯矩的计算结果与用地层-结构模型计算的隧道衬砌弯矩趋于一致;

3)根据用拉压弹簧荷载-结构模型对浅埋隧道衬砌弯矩计算结果(图10)可以看出,拉弹簧弹性抗力系数与压弹簧弹性抗力系数之比在1/3～2/3之间时,考虑应力拱效应的荷载-结构计算模型对隧道衬砌弯矩的计算结果与用地层-结构模型计算的隧道衬砌弯矩趋于一致;

4)无论深埋还是浅埋隧道,考虑应力拱效应的荷载-结构计算模型计算所得隧道衬砌弯矩与用地层-结构模型计算得到的隧道衬砌弯矩趋于一致,但在数值上2种计算方法计算得到的弯矩并不相等,这主要是因为从荷载-结构法与地层-结构法2种计算方法的计算原理看,荷载-结构法的计算结果要比地层结构法的计算结果大.

[1] 刘建航,候学渊.盾构法隧道[M].北京:中国铁道出版社,1991.

[2] Working Group No.2 International Tunneling Association. Guidelines for the design of shield tunnel lining[J].TunnelingandUndergroundSpaceTechnology,2000,15(3):303-331.

[3] 喻渝,陈中,王明年.隧道设计计算模型对围岩适应性的探讨[J].现代隧道技术,2004,41(4): 7-12.

[4] 汪成兵.软弱破碎隧道围岩渐进性破坏机理研究[D].上海:同济大学,2007.

[5] 重庆交通科研设计院.JTG D70-2004 公路隧道设计规范[S].北京:人民交通出版社,2004.

[6] 朱合华,崔茂玉,杨金松.盾构衬砌管片的设计模型与荷载分布的研究[J].岩土工程学报,2000,22(2):190-195.