基于蚁群算法的体绘制视点优化
2013-11-19张尤赛
张尤赛,辛 莉
(江苏科技大学 电子信息学院,江苏 镇江 212003)
体绘制是一种非常重要和灵活的体数据可视化技术.由于用户对体数据可视化的多样性要求和体绘制过程中频繁的人机交互操作,使体绘制的适应性和效率大大降低,从而阻碍了体绘制技术的推广应用.利用智能算法为用户提供最佳视点或一组被优化的视点集,以便用户准确、快速地理解体数据中的重要信息,是提高体绘制效率的一种可行的途径.
体绘制的最佳视点选择可以归结为优化问题.首先需要解决的是视点的评价问题,即怎样的视点是一个最佳视点,目前为止,视点的评价尚没有一个统一的标准,一般认为能够最大限度地体现体数据内部结构信息的视点,可以看作最佳视点.在信息理论中,通常采用信息熵来表示信源所含信息量的程度,信息熵值愈高表明信源所含的信息量愈大.目前,已有研究采用信息熵的形式,从不同的角度和因素出发,提出了体绘制最佳视点的评判方法,如文献[1-2]利用体数据的等值面、梯度模或结构特征集等结构信息来构造视点信息“熵”,以评价视点的质量;文献[3-4]则直接在3维体素上利用不透明度作为信息因素,定义视点信息“熵”来评价视点的质量.由于这些方法一般都涉及到3维数据场的数据分析和特征提取,因此数据处理量大,步骤较为复杂.体绘制视点优化问题需要解决的另一个问题是视点优化算法,即如何高效、可靠地得到体绘制的最佳视点或一组优化的视点集,以提高体绘制的绘制效果和效率.目前,在体绘制视点优化中采用的算法主要有粒子群算法(particle swarm optimizatin,PSO)、单纯形-粒子群混合算法(nelder-mead simplex search and particle swarm optimization,NM-PSO)和混合蛙跳算法(shuffled frog leaping algorithm,SFLA)等[5-7].从研究结果看,上述算法较好地解决了视点的优化问题,实现了最优视点的选择.但从总体研究来看,体绘制视点优化算法的研究还不够充分,有许多优秀的智能算法尚未涉足到该领域.
文中提出了一种基于蚁群算法(ant colony algorithm,ACA)的体绘制视点优化方法.该方法利用体数据2维投影图像的不透明度和结构信息特征,用信息熵的形式构造了视点评价函数;在视点优化的过程中,将视点评价函数作为ACA的目标函数,利用ACA自动地实现视点的优化迭代,最终得到全局最优视点或一组优化的视点集,从而减少了体绘制过程中的交互操作,有效地提高了体绘制的效率.实验结果表明,该方法与基于SFLA的视点优化算法具有相近似的性能,比基于PSO和NM-PSO的视点优化算法具有更好的收敛稳定性、收敛效率和收敛精度.
1 基于信息熵的视点评价
文献[3]通过给每个体素j定义一个重要性因子Wj,并将体素j与视点V之间的透明度作为体素的可见性vj(V),采用式(1)来表示视点V的信息熵.
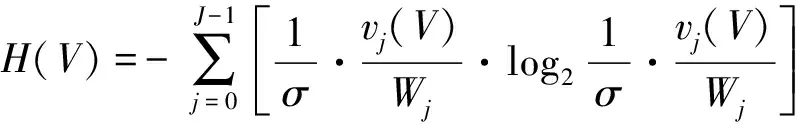
(1)
式中,H(V)为视点V的信息熵,J为体数据中体素的总数.
由于式(1)需要在体数据的3维空间中对体数据的内部结构进行分析,才能确定重要性因子Wj和可见性vj(V),所以往往会带来大量复杂的数据计算和分析.为了克服这种不足,文中在体数据投影图像的2维空间,利用像素的不透明度及其结构信息因子来构建视点的信息熵,作为视点质量的评价函数,如式(2)所示.
(2)
0≤wαi,wαj≤1
式中:J为体数据2维投影图像中可见像素的总数;αi为像素i的不透明度;wαi为αi的结构信息因子.通常在αi的结构边缘处wαi→1,非边缘处wαi→0.
在视点优化过程中每次计算视点信息熵时,为了避免体数据2维投影图像显示所导致的不必要的时间损耗,采用了像素包装和解包技术[8],即将体绘制所得到的2维投影图像直接写入到处理器内存,并在内存中直接进行视点信息熵的计算和评价,而不必将2维投影图像通过图形管线写入帧缓冲区进行实际显示,从而避免了在图形管线中所消耗的时间.
为了验证视点信息熵式(2)的评价效果,图1给出了应用3维纹理映射和Phong光照模型的体绘制技术[9],对人颅骨体数据进行视点评价的实验结果.实验中让视点围绕人颅骨的3维重建图像做360°的水平旋转,每隔1°进行一次视点评价.结构信息因子wαi采用归一化的Sobel算子对体绘制2维投影不透明度图像进行滤波来获得.图1a)为视角水平旋转时视点信息熵的变化曲线,图1b),c),d),e)分别是视角θ为0°,90°,205°和330°下人颅骨的3维成像.其中,0°视角对应于视点信息熵的最大值2.97,为最优视点,205°视角对应于视点信息熵的最小值2.80,为最差视点.
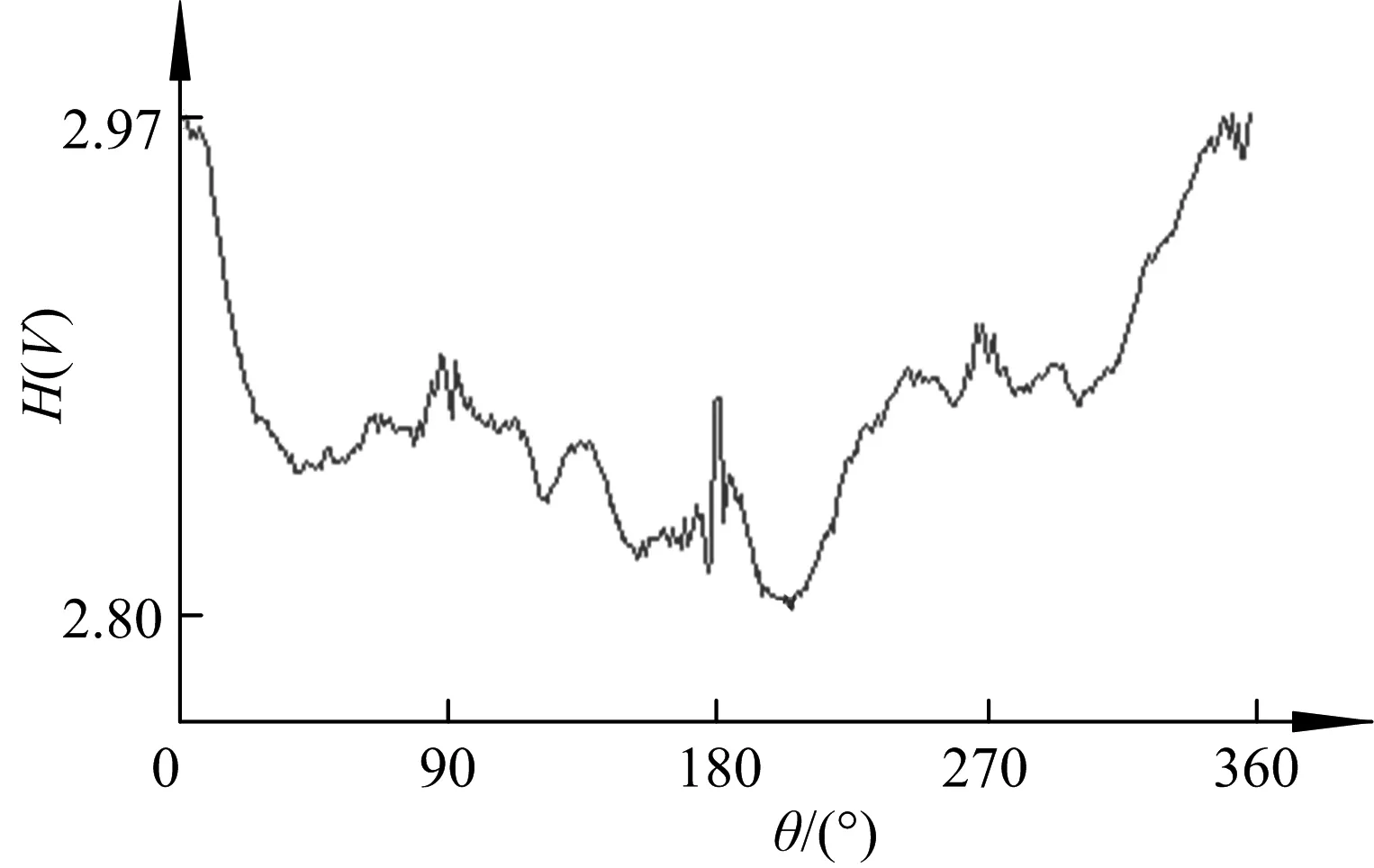
a) 视点评价函数值随视点角度变化曲线
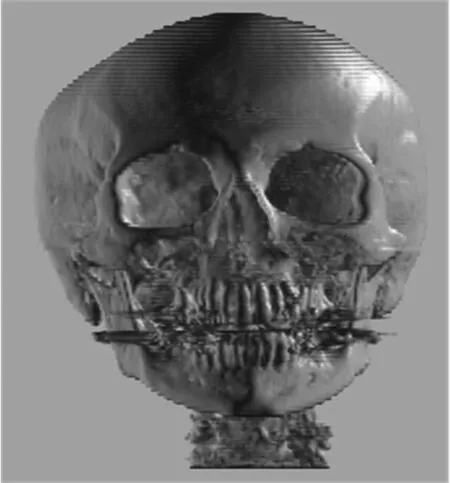
b) 视角0°
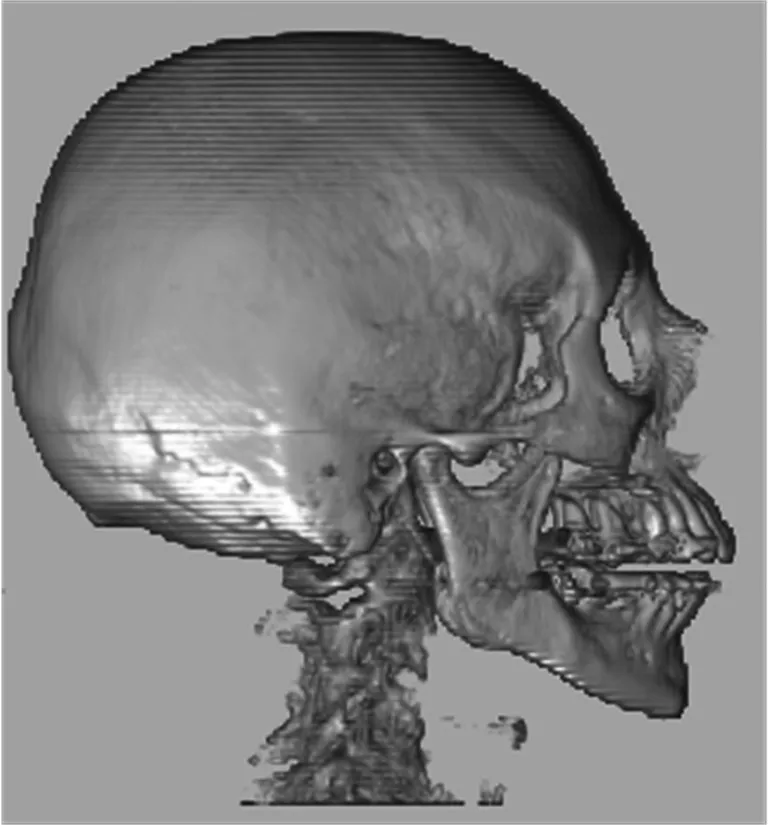
c) 视角90°
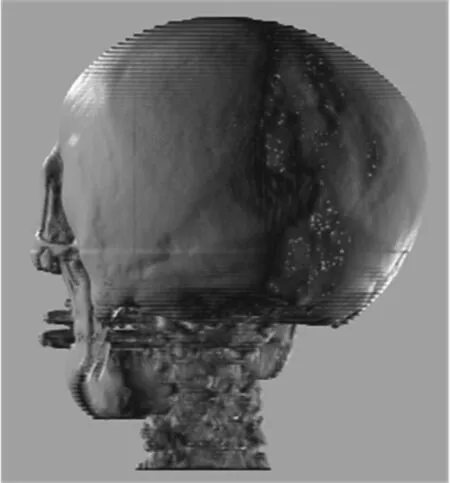
d) 视角205°

e) 视角330°
图1人体颅骨体数据的视点评价实验
Fig.1ViewpointevaluationexperimentofCTvolumetricdataofhumanbrain
2 体绘制视点的蚁群优化算法
2.1 蚁群算法的原理
蚁群算法是一种模拟蚂蚁群体觅食行为方式的仿生优化算法[10].该算法引入正反馈并行机制,具有较强的鲁棒性、优良的分布式机制和适用性强、易与其它算法相结合的特点.目前蚁群算法已经成功应用于很多领域,可以解决一维或多维、连续或离散、静态或动态等优化问题[11-13].
蚁群算法的原理:根据问题的性质估计出各变量的取值范围,对取值范围进行N等分.则每个变量对应于N+1个节点,M个变量即为M级,构成了共有M×(N+1)个节点组成的解空间.蚁群在优化过程中,每只蚂蚁在第1级到第M级各节点之间移动,形成一条行进路径,并在所经历的节点上根据目标函数值留下一定的信息素,并利用信息素的积累和挥发作用产生节点的转移概率,以影响整个蚁群的寻优路径,使得目标函数值大的节点积累的信息素值较大.整个蚁群通过不断的循环优化,每次循环都可得到一个信息素最大的节点,作为当前最优解,并据此逐渐收缩搜索范围,直至变量节点之间的距离满足预先设定的精度为止,算法结束.最后将信息素最大的节点及其对应的目标函数值作为最优解输出.
2.2 体绘制视点优化的蚁群算法实现
体绘制视点的蚁群优化算法的基本原理是利用ACA在整个视域内,寻找出视点信息熵值最大的视点或若干视点信息熵值较大的视点,作为观察体数据的最优视点或一组优化的视点集.在基于ACA的视点优化问题中,假设利用体绘制重建的3维图像中心位于坐标的原点,视点位于以坐标原点为球心的单位球面上(为方便起见,将该单位球面称为视域球),整个视域球构成了视点优化的解空间.视点k的坐标可以用位于视域球上的单位矢量V(k)=[α(k),β(k)]来表示,其中α(k)∈[0°,360°]为V(k)在XZ平面上投影矢量与X坐标轴的夹角,β(k)∈[0°,180°]为V(k)与Y坐标轴之间的夹角.在蚁群算法中,每个蚂蚁的一条行进路径代表一个可选的视点,可以用V(k)来表示,整个蚁群的路径构成了一个视点集{V(k)};蚁群算法的目标函数则可以用节点上的视点信息熵H[V(k)]表示.
图2为基于蚁群算法的体绘制视点优化流程.
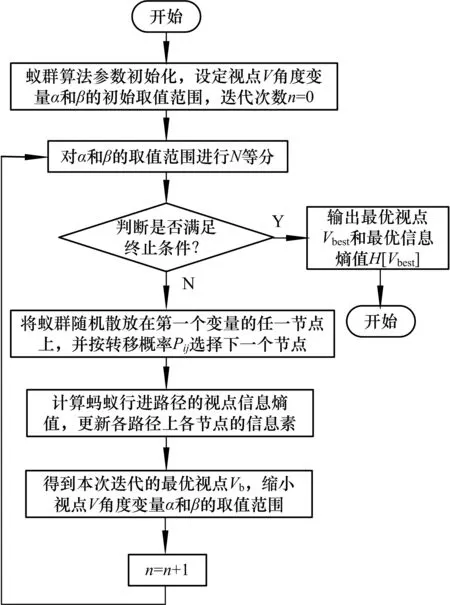
图2 基于蚁群算法的体绘制视点优化流程Fig.2 Flow chart of viewpoint optimization based on ant colony algorithm for volume rendering
算法的具体实现如下:
1)设置信息素常量Q,信息素挥发系数ρ,各节点的初始信息素τconst和蚂蚁总数Nants等蚁群算法参数;调整视点角度变量α,β的取值范围,αl≤α≤αu,βl≤β≤βu;初始迭代时,αl=0°,αu=360°,βl=0°,βu=180°;设算法迭代次数n=0.
2)对变量的取值范围进行N等分,hα,hβ表示变量各等份的长度:
(3)
3)判断是否满足算法终止条件:
max(hα,hβ)≤ε
(4)
若满足,输出最优视点Vbest=[αbest,βbest]和最优视点信息熵值H[Vbest];否则,转步骤4).
(5)
4)将蚁群随机撒放在第一个变量的N+1个节点上.每只蚂蚁按转移概率Pij选择路径(下一个节点),并按式(7)对各节点信息素进行更新.

(6)
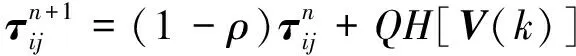
(7)
式中:τij表示第i个变量的第j个节点的信息素;H[V(k)]为蚂蚁k的目标函数值.
5)所有蚂蚁循环若干遍后,找出τij矩阵中每列最大的元素对应的行rowα,rowβ,即得出本次迭代的最优视点Vb,并按式(9,10)缩小变量的取值范围.
Vb=(αb,βb)=(αl+hα×rowα,βl+hβ×rowβ)
(8)
(9)
(10)
式中:Δ为变量取值范围的缩小步长,其更新公式为:Δ=ceil[N/(n+1)],n为蚁群优化的迭代次数.
6)n=n+1,转步骤2).
3 实验结果分析
实验选择了一组典型的体数据集,利用基于3维纹理映射的体绘制方法,将文中算法分别与基于PSO,NM-PSO和SFLA的视点优化算法进行了性能比较,以验证文中算法的性能.实验的硬件环境为Intel Pentium(R) Dual-Core CPU E5400 2.7 GHz,内存2.0 GB,Nvida GeForce 210图形卡(显存1 GB),软件平台为Visual C++6.0,OpenGL 2.0.
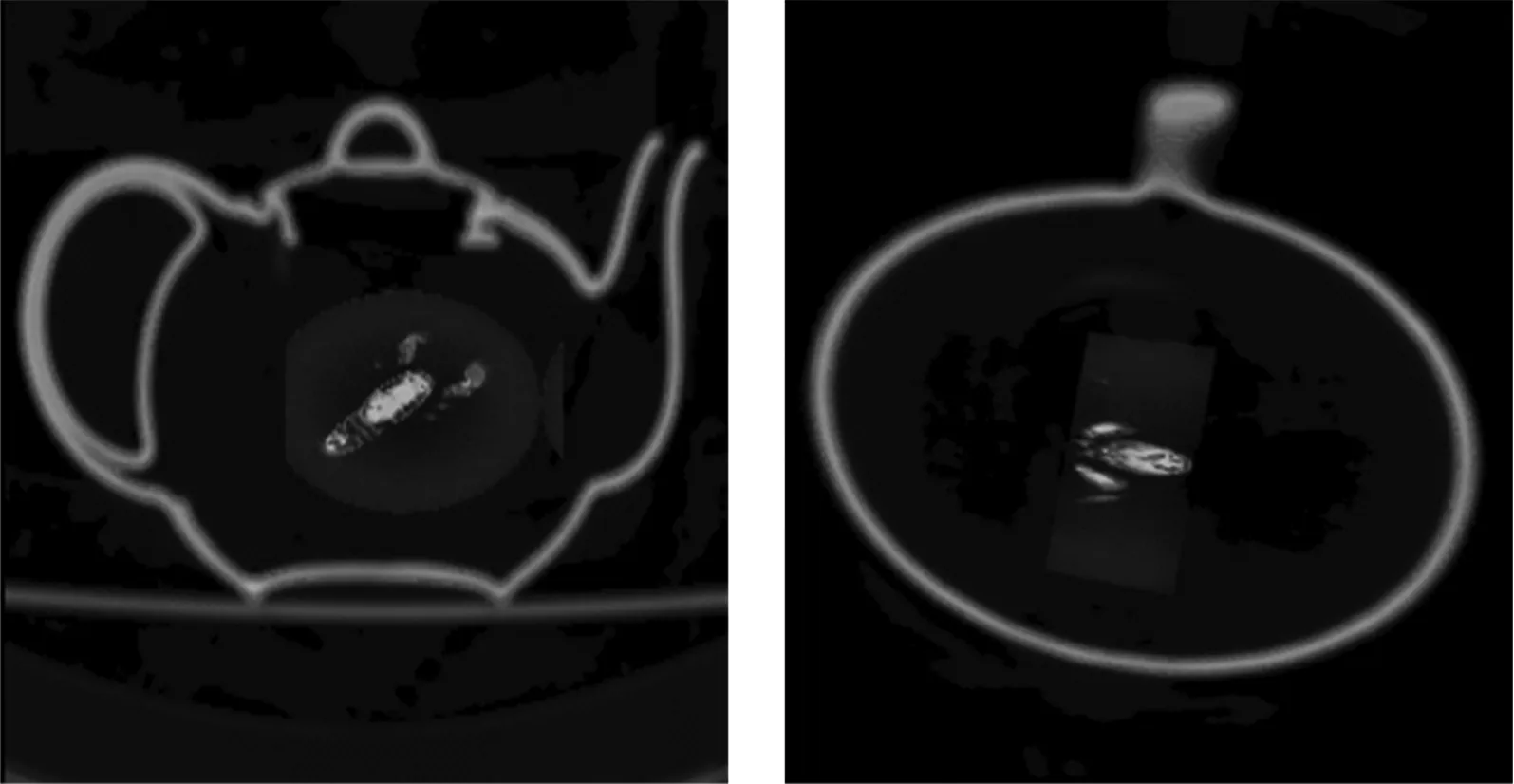
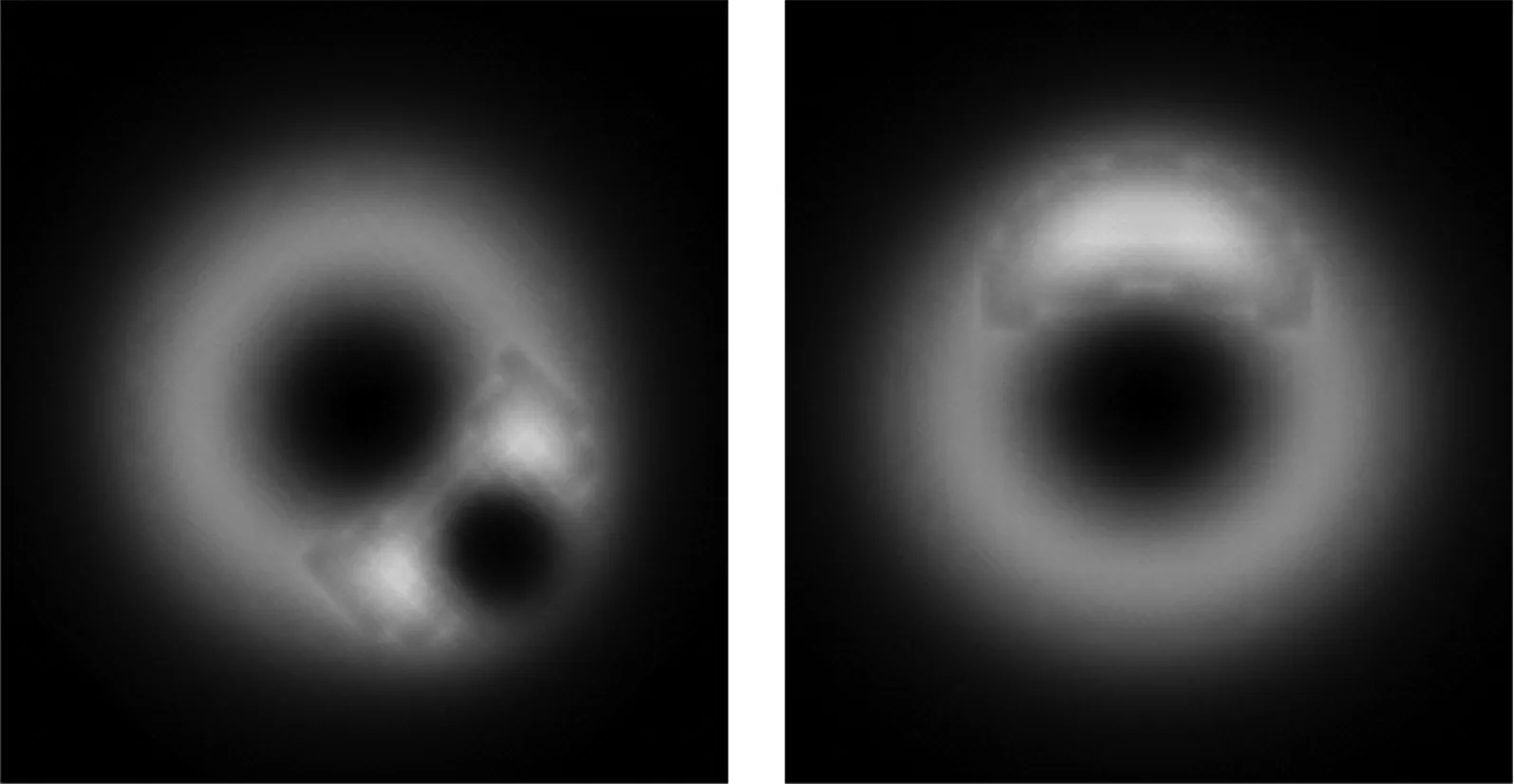
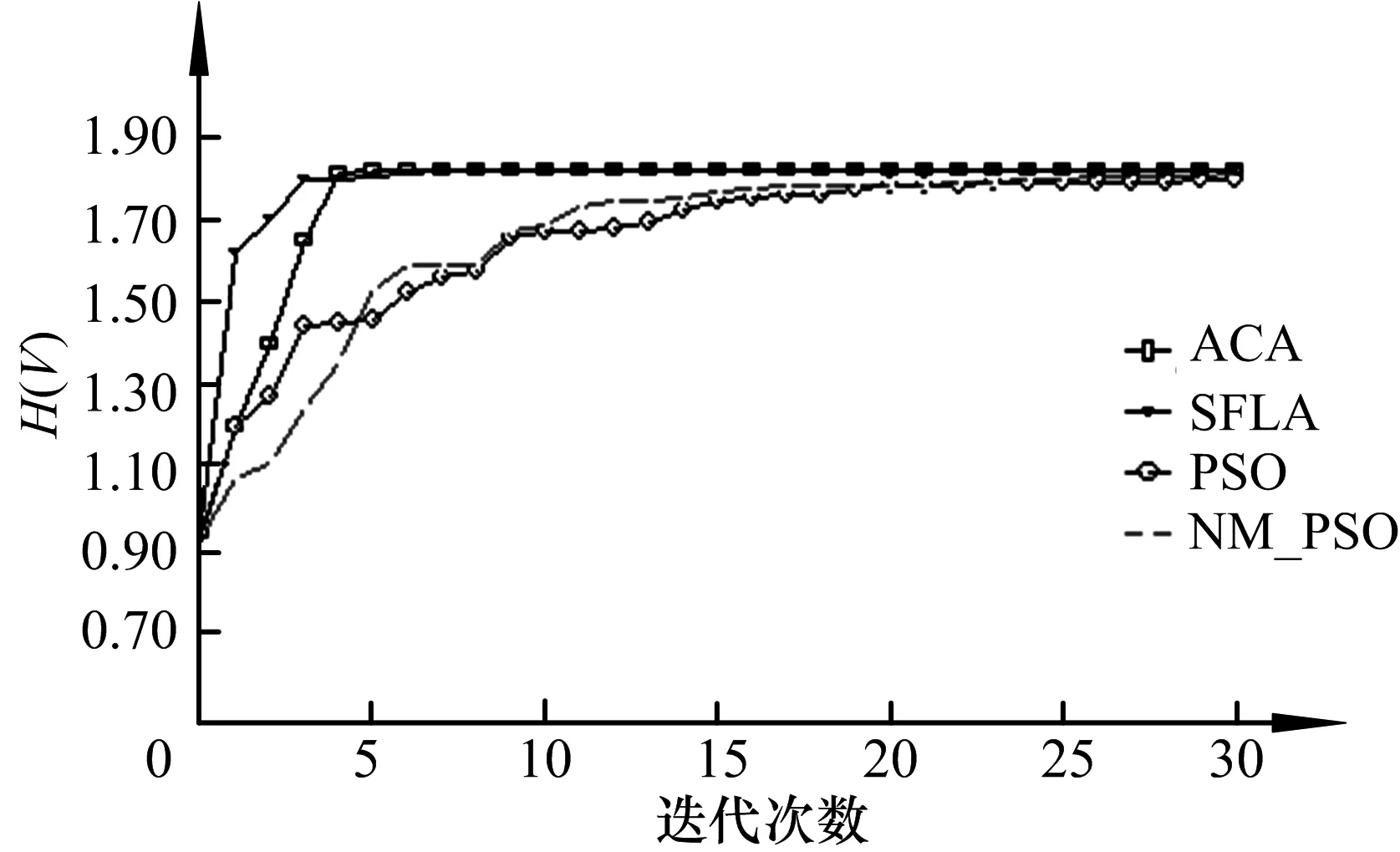
为了便于对上述4种算法的性能进行比较,实验中PSO,NM-PSO,SFLA和ACA4种算法的群体规模都取12.PSO算法的加速度系数c1=c2=2,惯性权重ω随着迭代次数在0.9~0.4之间线性递减;NM-PSO算法将5个最优粒子构成一组,进行NM单纯形局部搜索,NM的扩张系数γ=2,压缩系数β=0.5,剩余的7个粒子构成另一组,利用PSO算法进行全局优化;SFLA将蛙群分为3个模因组,每组模因组有4个青蛙,局部深度搜索6次;ACA算法的N"=12,Δ=ceil[N/(n+1)],ρ=0.2,Q=10,τconst=20~30.图3为利用文中方法对人脚趾、颅骨医学体数据、茶壶、原子核体数据进行实验所得的最优视点和最差视点的体绘制图像.图4给出了4种算法分别对上述4种体数据进行6次视点优化实验,完成30次迭代后所得到的视点信息熵的平均进化曲线.
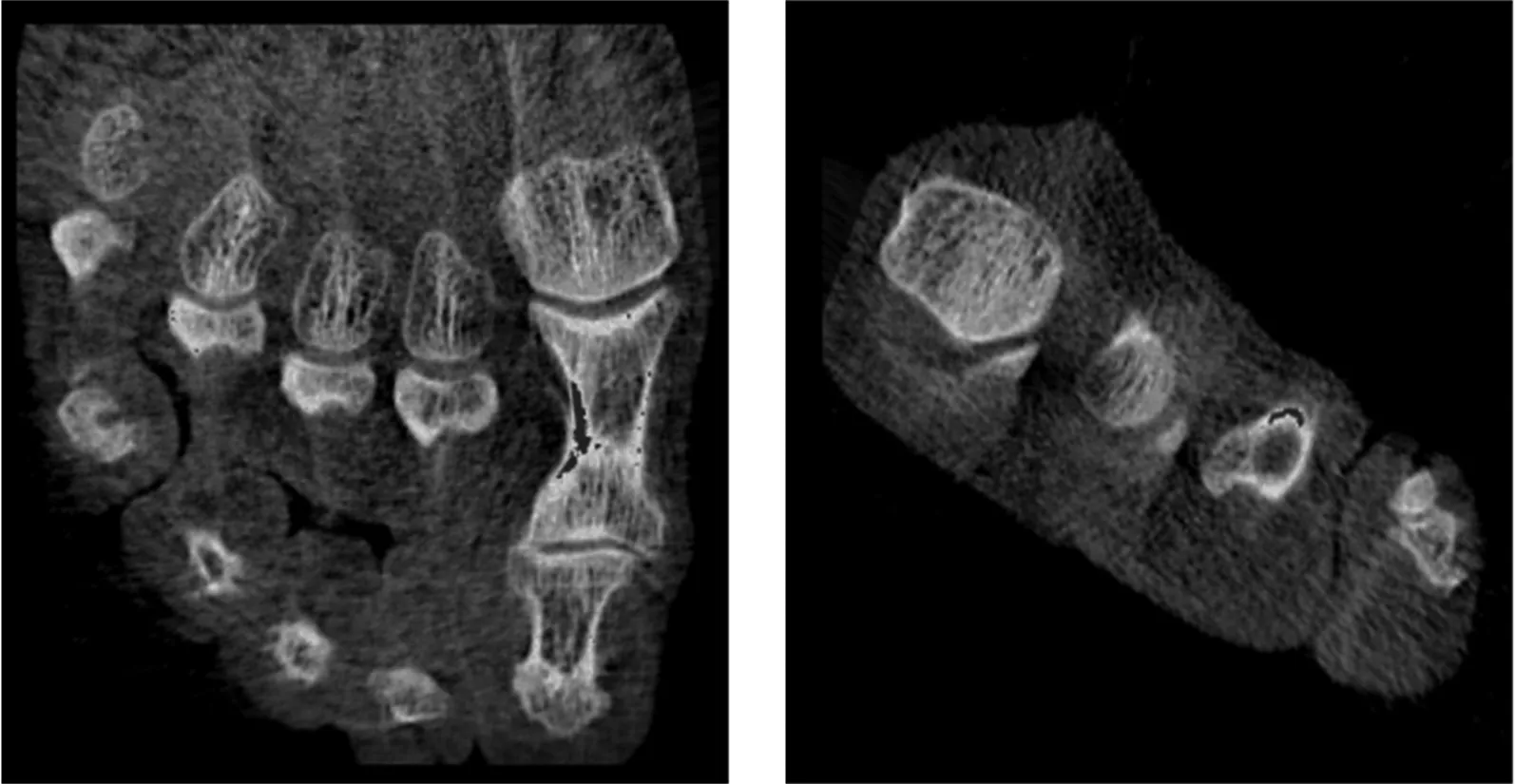
最优视点 最差视点
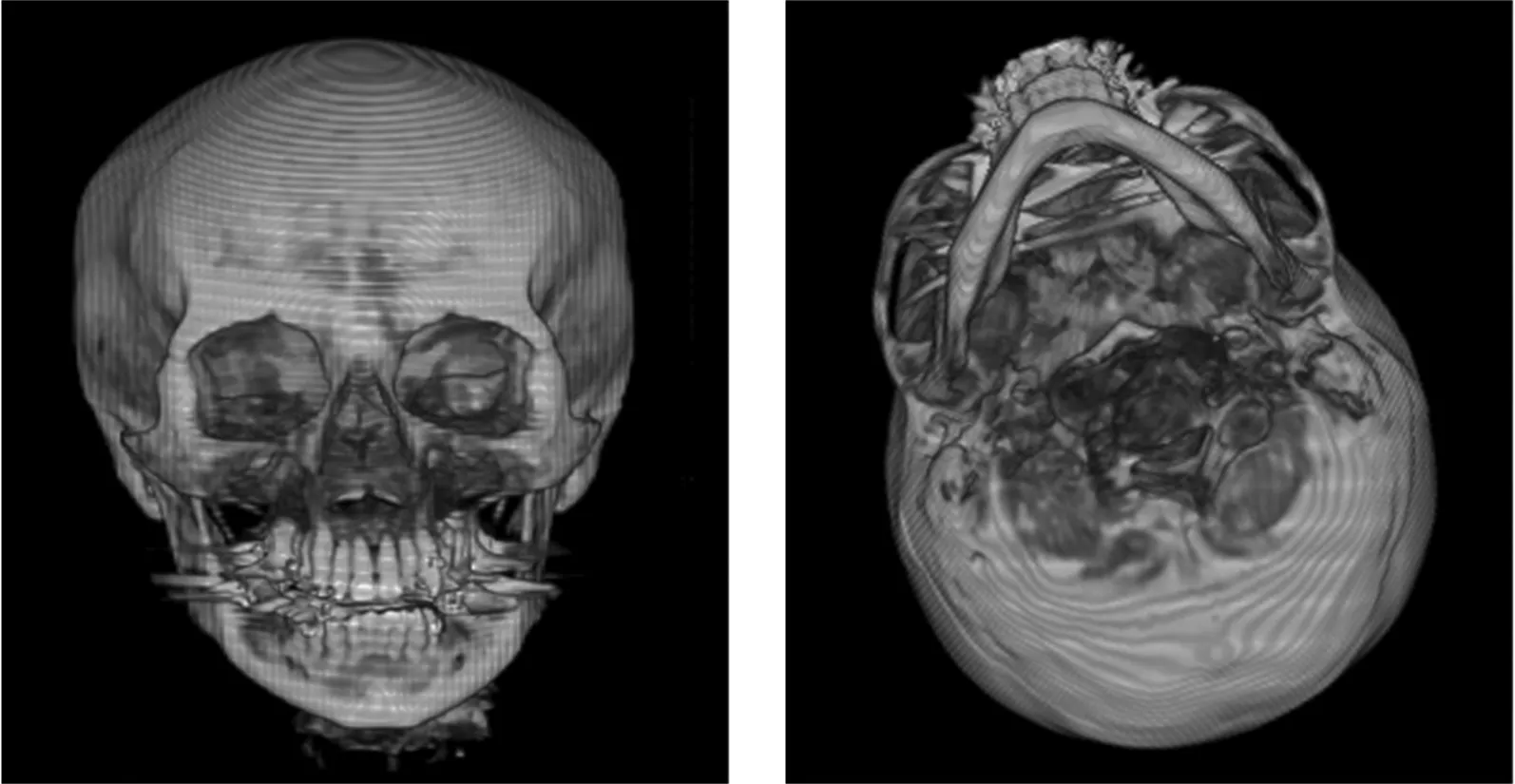
最优视点 最差视点
最优视点 最差视点
最优视点 最差视点
a) 人脚趾视点信息熵的平均进化曲线
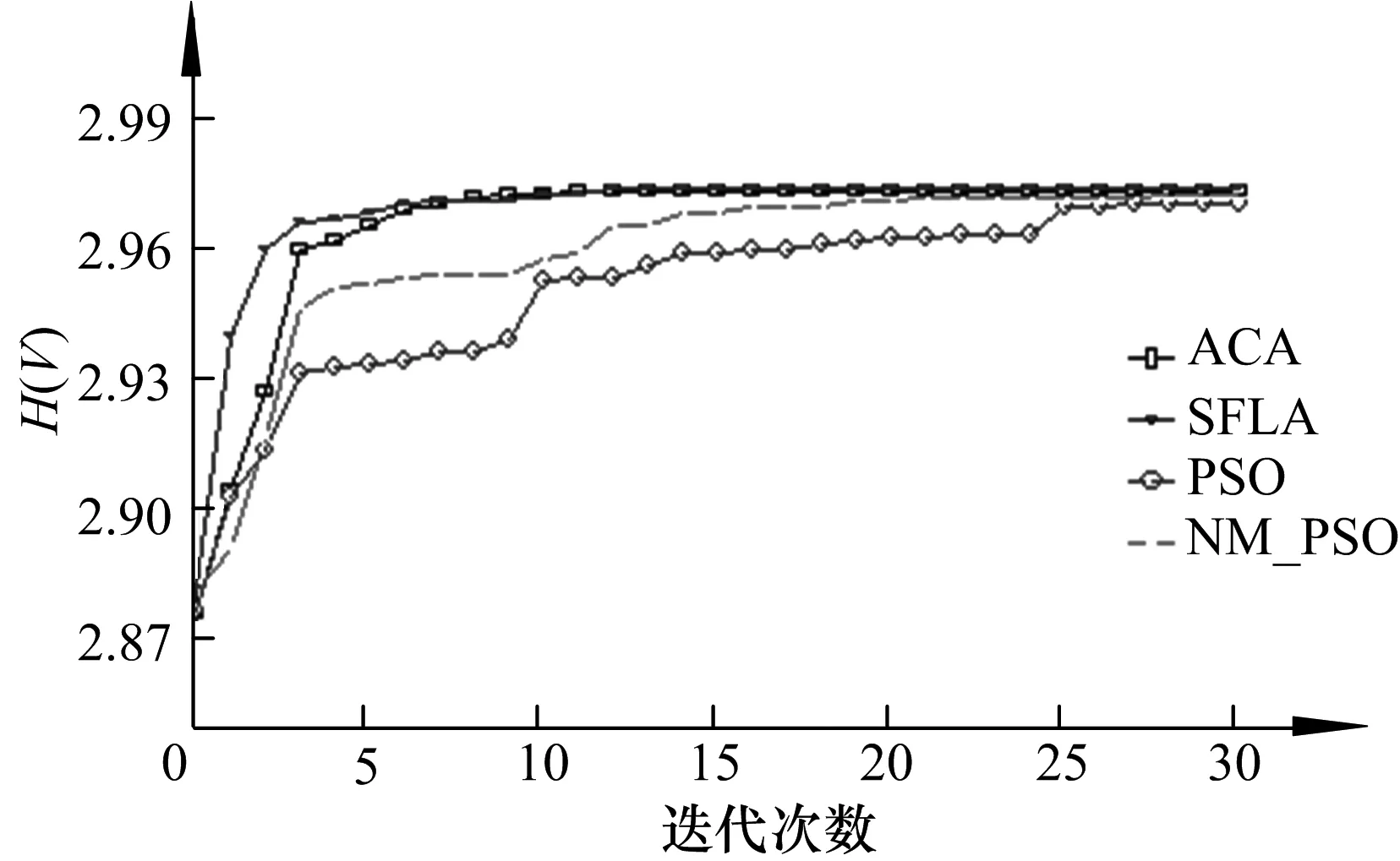
b) 人颅骨视点信息熵的平均进化曲线

c) 茶壶视点信息熵的平均进化曲线
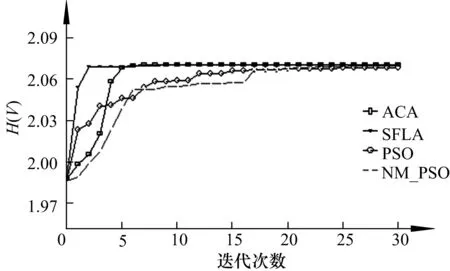
d) 原子核视点信息熵的平均进化曲线
综合上述实验结果,可以得出如下结论:
1)在算法的收敛效率方面,在初始的几次算法迭代中,基于SFLA的视点优化算法的收敛速度最快,文中算法其次,基于NM-PSO和PSO的视点优化算法的收敛速度较慢.体现出文中算法和基于SFLA的视点优化算法具有更好的算法迭代收敛效率.
2)在算法的实时性方面,由于算法的复杂度不同,SFLA算法每次迭代所需的时间较长,文中算法其次,PSO算法最快.但是由于算法每次迭代的收敛效率不同,SFLA算法和文中算法一般经过3~4次迭代即能接近最优解,经过7~12次迭代达到最优解;PSO和NM-PSO算法则需要经过25次以上的迭代才能接近或达到最优解.所以,文中算法和SFLA算法在视点优化的起始阶段,相比PSO和NM-PSO算法具有更好的实时性,但是在视点优化的后阶段在实时性上并不占有优势.
3)在算法的收敛精度方面,相比基于NM-PSO和PSO的视点优化算法,文中算法和基于SFLA的视点优化算法都可以得到更高的视点信息熵值,即具有更高的算法收敛精度.
4)蚁群算法中,蚁群运动时能根据目标函数值在所经历的节点上留下一定的信息素,并利用信息素的积累和挥发作用产生节点的转移概率,形成了一种正反馈并行机制,使蚁群个体之间可以交换局部优化信息,从而保证了整个蚁群对视点的全局优化能力和算法收敛的稳定性.
5)蚁群算法的参数较多,选择一组合适的参数,对蚁群算法的收敛性能有重要作用.文中算法在蚁群优化过程中,采用了一种非线性的变量缩小步长Δ=ceil[N/(n+1)],对避免小规模蚁群陷入局部最优解,提高蚁群算法的收敛性能具有很好的效果.
4 结论
利用反映体数据中体素重要性的不透明度和结构信息因子构建视点信息熵来评价视点的质量,在一定程度上反映了人类视觉系统的特性;文中利用蚁群算法进行体绘制的视点优化,较好地解决了体绘制最佳视点的选择问题,具有自动化和智能化的特点.但是,其不足的是在视点评价过程中,没有充分地体现出用户对最佳视点的个性化和多样性的要求,在视点优化过程中没有充分体现用户的偏好和习惯与智能算法的有机结合.
近年来,随着“大数据“概念的提出,大数据可视化问题必将成为新的研究热点.体绘制作为一种重要的体数据可视化技术,在数据简约可视化、高可扩展的数据投影、维度降解和高清晰显示等方面都面临着新的挑战,引入创新的视觉表现方式和用户交互手段,设计基于视觉感知的体绘制高效智能算法,都是值得进一步深入研究的课题.
[1] Takahashi S,Fujishiro I,Takeshima Y,et al.A feature-driven approach to locating optimal viewpoints for volume visualization[C]//Proceedingsofthe16thIEEEVisualization.Washington DC,USA: IEEE Press,2005: 495-502.
[2] Tao Yubo,Lin Hai,Bao Hujun,et al.Structure-aware viewpoint selection for volume visualization[C]//IEEEPacificVisualizationSymposium.Beijing,China: IEEE Computer Society,2009:193-200.
[3] Bordoloi U D,Shen H W.View selection for volume rendering[C]//Proceedingsofthe16thIEEEVisualization.Washington DC,USA: IEEE Computer Society,2005: 487-494.
[4] Ji Guangfeng,Shen Hanwei.Dynamic view selection for time-varying volumes[J].IEEETransactionsonVisualizationandComputerGraphics,2006,12 (5): 1109-1116.
[5] Wang Yanni,Zhou Dibin,Zheng Yao,et al.Viewpoint selection using PSO algorithms for volume rendering[C]//ProceedingsoftheSecondInternationalMulti-SymposiumsonComputerandComputationalSciences.Washington DC,USA: IEEE Press,2007: 286-291.
[6] Zhang Yousai,Wang Bin,Dai Changjiang.Viewpoint selection based on NM-PSO for volume rendering[C]//LectureNotesinComputerScience,7390LNAI,IntelligentComputingTheoriesandApplications-8thInternationalConference,ICIC2012Proceedings.Huangshan,China: Springer Verlag Press,July 2012: 487-494.
[7] 张尤赛,王彬.应用混合蛙跳算法的体绘制最佳视点选择[J].中国图象图形学报,2011,16(9): 1670-1675.
Zhang Yousai,Wang Bin.Optimal viewpoint selection for volume rendering using shuffled frog leaping algorithm[J].JournalofImageandGraphics,2011,16(9): 1670-1675.(in Chinese)
[8] Shreiner D,The Khronos OpenGL ARB Woring Group.OpenGL编程指南[M].7版.李军,徐波,译.北京: 机械工业出版社,2010:209-224.
[9] 张尤赛,陈福民.基于纹理映射与Phong光照模型的体绘制加速算法[J].中国图象图形学报,2003,8(9):1048-1054.
Zhang Yousai,Chen Fumin.Accelerated volume rendering using texture mapping with phong shading [J].JournalofImageandGraphics,2003,8 (9): 1048-1054.(in Chinese)
[10] Colorni A,Dorigo M,Maniezzo V.Distributed optimization by ant colonies[C]//ProceedingsofEuropeanConferenceonArtificialLife.Paris,France:Elsevier Publishing,1991:134-142.
[11] 段海滨,马冠军,王道波,等.一种求解连续空间优化问题的改进蚁群算法[J].系统仿真学报,2007,19(5): 974-977.
Duan Haibin,Ma Guanjun,Wang Daobo,et al.Improved ant colony algorithm for solving continuous space optimization problems[J].JournalofSystemSimulation,2007,19(5): 974-977.(in Chinese)
[12] 陈琪,宁博.MMAS在带时间窗的车辆路线问题中的应用[J].江苏科技大学学报:自然科学版,2009,23(3): 263-266.
Chen Qi,Ning Bo.Application of MMAS on vehicle routing problem with time window[J].JournalofJiangsuUniversityofScienceandTechnology:NaturalScienceEdition,2009,23(3): 263-266.(in Chinese)
[13] 陈立伟,唐权华.基于蚁群算法的离散救援问题出救点选址研究[J].计算机应用研究,2010,27(11): 4152-4154.
Chen Liwei,Tang Quanhua.Research on depot location of discrete emergency aid based on ACO[J].ApplicationResearchofComputers,2010,27(11): 4152-4154.(in Chinese)
