基于速度矩分布的喷水推进泵反设计及抗汽蚀性能分析

马文昌,曹 辉,宋少雷

(1.海装沈阳军事代表局,辽宁 沈阳 110003)(2.海军驻上海江南造船(集团)有限责任公司军事代表室,上海 201913)

50年代初,提出了S1/S2流面的概念,此方法开始广泛应用于叶轮的设计和分析计算.基于平均S2流面的反问题设计方法主要有两种:给定速度矩vθr分布和给定轴面流速Wm分布[1].基于S2流面并给定vθr分布的反问题设计方法在离心式及混流式叶轮的设计中得到广泛的应用.给定沿流线的vθr分布,实际上就是给定了沿流线叶片上的负荷分布,从而可以控制叶片的空间形状.文献[2]提出过一种基于速度矩vθr分布离心式压缩机叶轮叶片的设计方法,文献[3]在给定载荷分布即vθr分布的情况下,用有限元法和积分法通过迭代求解考虑vθr分布影响的S2流面轴对称流场和叶片的骨面方程.文中基于S1/S2流面理论,给定初始轴面流道形状,以速度矩分布和厚度分布为已知条件,实现喷水推进泵的反问题设计,进行实体建模并对模型泵进行数值模拟分析,研究不同工况下喷水推进泵的压力分布、速度矢量、效率、扬程,汽蚀性等性能.

1 准三维反问题设计数学模型

由于喷水推进泵叶轮内部的流动非常复杂,叶片与水流之间相互作用相互影响,所以,准三维反问题设计方法是水泵叶轮设计较为合理的方法[4].用准三维方法描述叶轮运动规律时,假定叶轮中的流动是相对稳定的、无粘性的且不可压缩.

1.1 S2流面的基本方程

连续方程和运动方程为[5]:

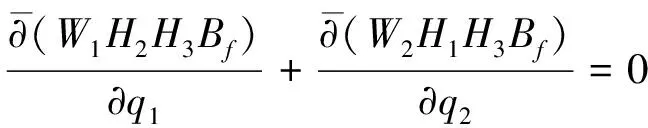
(1)

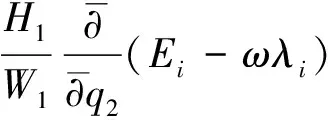
(2)

式中:Ei,λi分别为进口总能量和速度矩;Bf为排挤系数;W,V分别为相对速度和绝对速度;Hi为拉梅系数;

引入流函数Ψ,则:

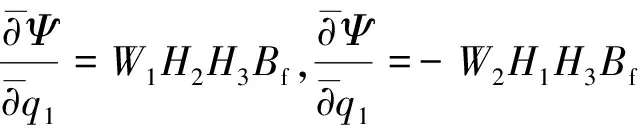
(3)

S2流面上的流函数方程为:

(4)

1.2 叶片设计的基本方程

假定流面为中心流面,其形状与叶片骨面重合.在正交曲线坐标系(q1,q2,q3)中,取q3=θ,则S2流面方程[6-7]为:

q3=θ(q1,q2)

(5)

写成空间曲面形式:

S(q1,q2,q3)=q3-θ(q1,q2)=0

(6)

于是有:

(7)

经推导可得出叶片方程为:

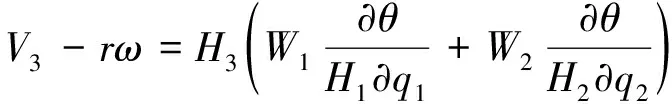
(8)

速度分量W1,W2在轴平面上,两者合成轴面速度Wm,m为轴面流线相对长度.因此,

(9)

用轴面流线坐标,骨线的构建方程为:

(10)

(11)

式中:vθr为速度矩分布函数；θ为叶片骨线角坐标；ω为角速度；l为轴面流线长.

在方程组中,只要给定速度矩v3r(即vθr)沿轴面流线的分布规律,即可使方程组封闭.

1.3 速度矩分布规律

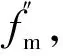
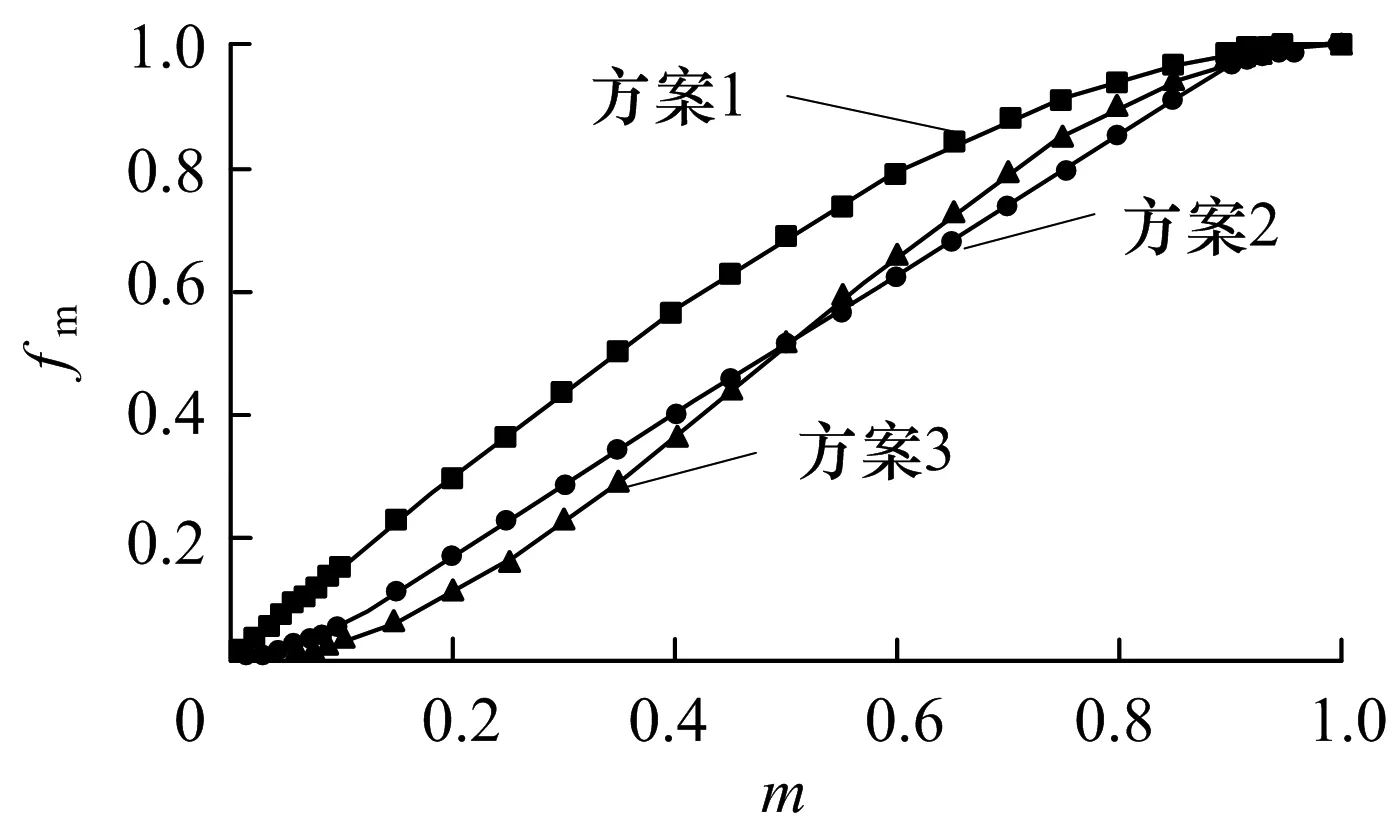
图1 无量纲速度矩分布函数fmFig.1 Dimensionless velocity moment distribution function fm

给定叶轮进出口无量纲速度矩,设进口速度矩为vu1r,出口速度矩vu2r，叶片进出口的速度矩差值为：

Δvur=vu2r-vu1r

(12)

因此,速度矩沿轴面流线的变化规律可表示为:

(13)

式中:a,b,c,d,e为系数,一般假定叶片进口处vθr为0,出口处vθr为1,进口处为减少汽蚀设定dfm/dm=0,另外再任取一点给定数值,这时即可确定5个系数.

1.4 叶片加厚

S1流面是以轴面流线为母线的回转面,建立坐标系(m,θ,k),S1流面可看作是k=c(常数)时的准二维平面,轴面流线m为一个回转面与子午面的交线[8].

由前面计算得出叶片骨线后在(m,θ)平面上进行加厚.为方便计算,引入坐标变换,把骨线保角变换到(x,y)平面上,并按一定叶片厚度分布规律进行加厚:

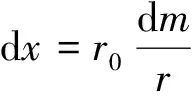
(14)

dy=r0dθ

(15)

2 准三维反问题设计步骤

文中采用Fortran语言编程实现喷水推进泵反问题设计.S2流面的主要计算步骤如下:

1)给定初始轴面流道形状,划分轴面流道网格,在给定相应的求解边值条件下,计算边界及内部所有节点的流函数值Ψj,从而求解初始轴面流场,并给定转速、叶片数等基本参量;

2)给定速度矩vθr及叶片厚度沿轴面流线的分布规律;

3)求解W1，W2,并可求出轴面速度Wm;

4)求解叶片骨线角坐标θ;

5)离散连续方程,给定右端残差(Res)i,j及迭代次数,修正所计算流函数Ψj直至满足方程,从而得到新的流线;

6)重复步骤3),4),5)直至两次循环流线位置的误差小于给定值.

3 喷水推进泵设计结果

在设计转速1 000 r/min、流量2.7 m3/s、扬程22 m的设计工况下,采用3种不同的速度矩分布规律,采用Fortran语言编程计算得到不同喷水推进泵基本数据,包括喷水推进泵的三维坐标、叶片平面绘形坐标、轴面流网坐标、流函数值、叶片表面压力系数分布、残差值等.将数据采用三维造型软件处理后得到实体化模型.喷水推进泵叶轮模型如图2.

图2 喷水推进泵叶轮模型Fig.2 Water jet boost pump impeller model

4 喷水推进泵数值模拟和抗汽蚀性能分析

4.1 数值模拟计算方法

对根据上述方法设计得到喷水推进泵模型采用三维数值模拟的方法,计算得到其流场特性并对其性能和抗汽蚀能力进行分析.数值模拟过程中,采用有限体积法离散控制方程和标准k-ε两方程湍流模型.具体方程限于篇幅不再给出.

进出口均设定压力边界条件,参考压力设为0,进口给定绝对总压为一个标准大气压.由于在临近固壁的地方,雷诺数一般很低,标准k-ε模型用在充分发展的湍流区域内是不适用的,因此在固壁处采用壁面函数法.在干涉面上使用混合面Mixing Plane模型.混合面定义在上游通道的出口与动叶区的进口以及动叶区的出口与静叶区的进口这两个交接处.

对于喷水推进泵全流道,由于叶轮及导叶体内流道结构复杂,叶片比较扭曲,因此全部采用四面体非结构网格进行划分.为了更好的捕捉流场内的汽蚀信息及二次回流等现象,对叶片及轮毂均进行了局部加密,计算流场区域的计算网格总数约为245.5万个.图3为喷水推进泵网格划分和计算区域.

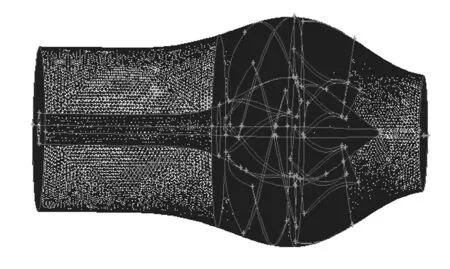
图3 喷水推进泵总体网格划分Fig.3 Water jet propulsion pump meshing

4.2 计算结果和抗汽蚀性能分析

通过数值模拟计算,在设计转速1 000 rpm时,对3个泵模型进行外特性预测分析.在保证流量和扬程关系基本不变的前提下,泵的效率—流量变化较明显.流量—效率曲线表明,随着流量的增加,泵的效率降低,在设计流量附近效率达到最高.针对不同速度矩方案设计的喷水推进泵,高效区分布个别差别明显,采用方案1效率比较低，方案2、方案3设计的泵叶轮效率高,最高效率可达91.3%.分析其主要原因在于叶片的速度矩分布的改变对叶片的形状、性能影响较大.图4为流量Q—效率η性能曲线.

在叶轮区域,随着半径R的增大,介质水的圆周速度增大,叶片外缘靠近进口边区域是汽蚀易发区.根据3种速度矩分布方案设计的喷水推进泵,在动叶叶背汽蚀面积如图5～7.在最高效率点工况时,叶轮叶背径向截面上R=300 mm的汽蚀区域比较如图8～10.

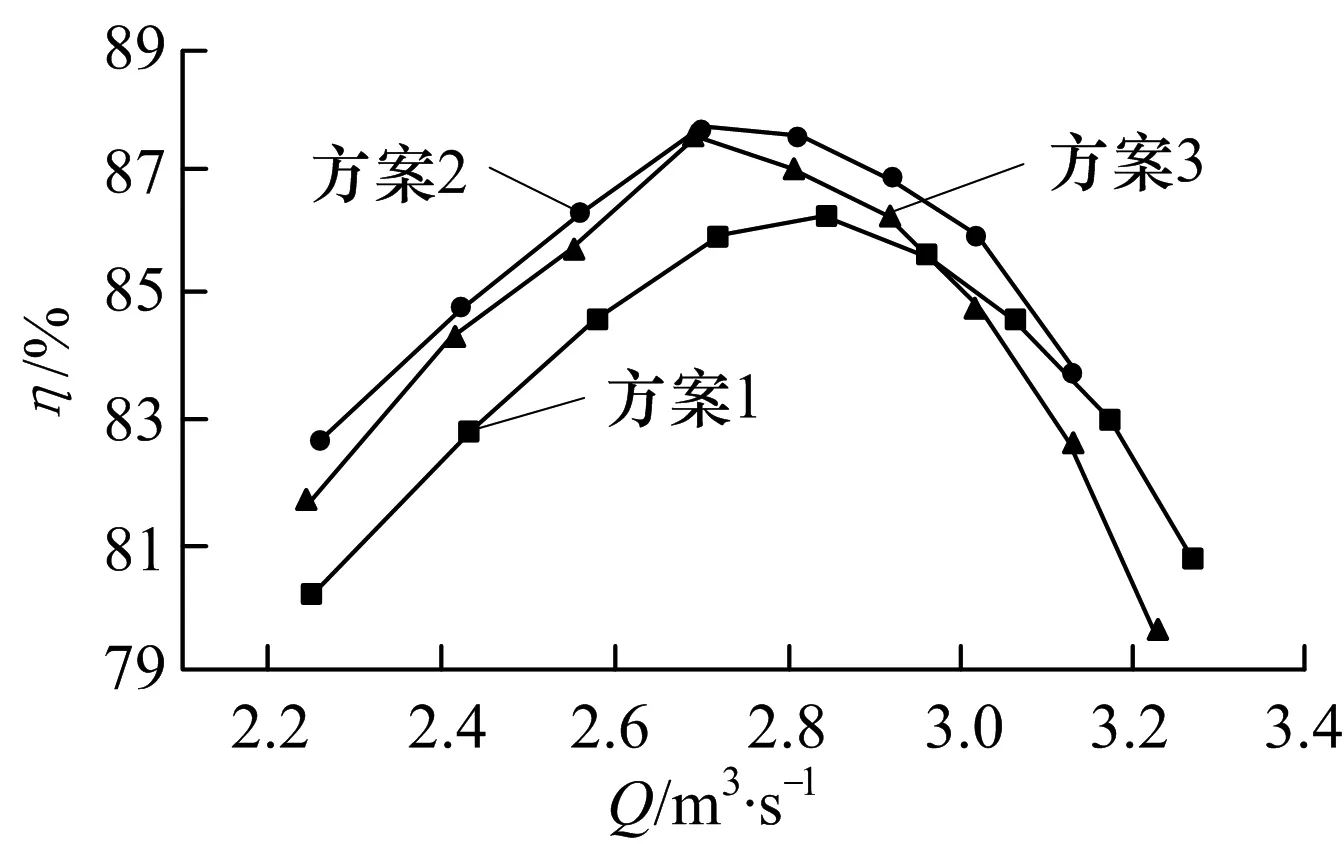
图4 流量—效率性能曲线Fig.4 Flow capacity-efficiency performance curve

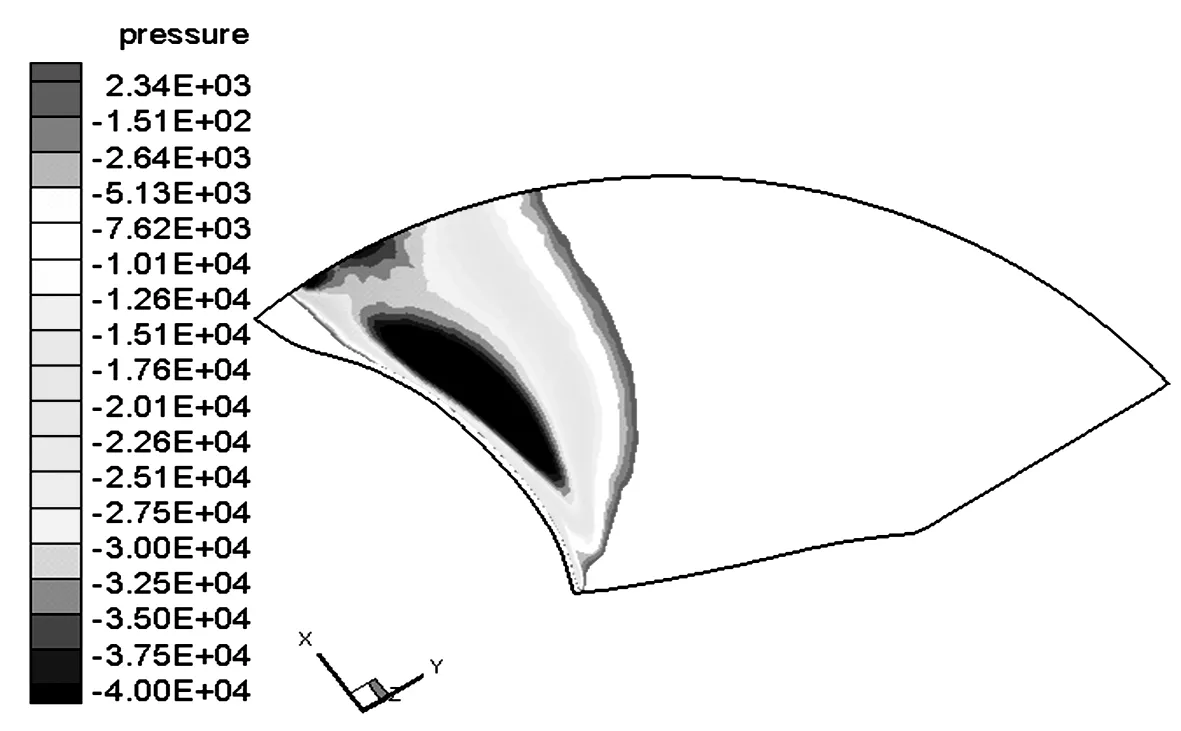
图5 方案1动叶叶背汽蚀面积Fig.5 Scheme I rotor blade back cavitation area

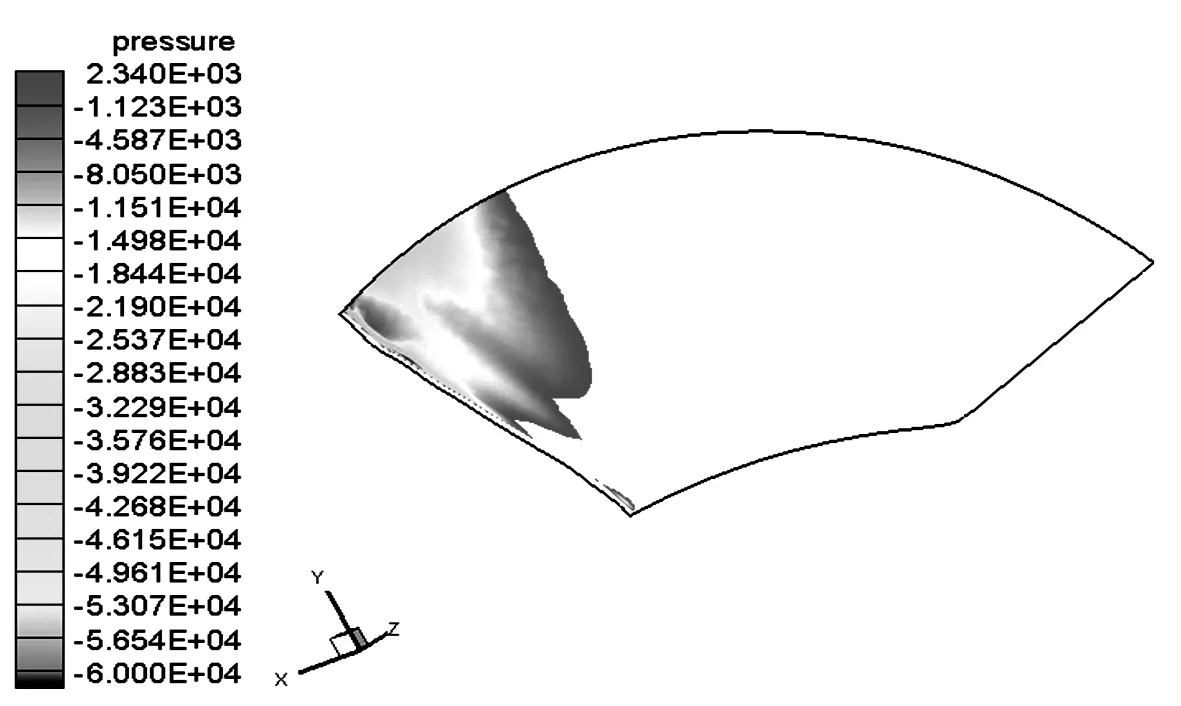
图6 方案2动叶叶背汽蚀面积Fig.6 Scheme II rotor blade back cavitation area

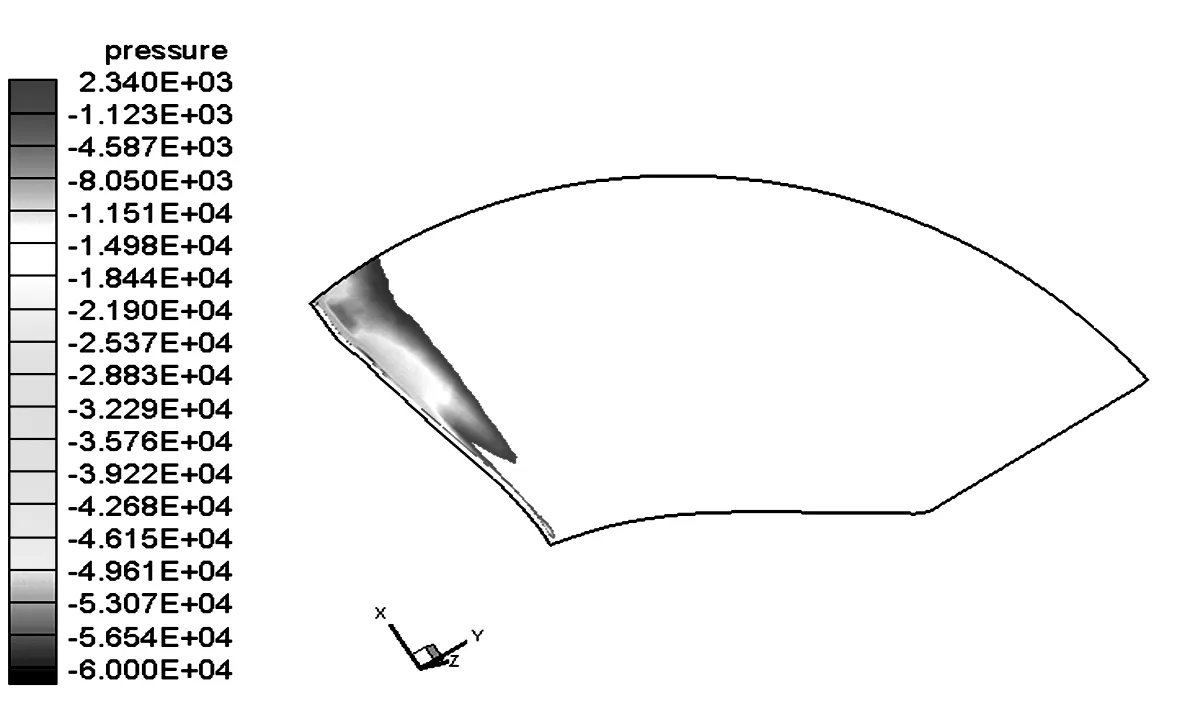
图7 方案3动叶叶背汽蚀面积Fig.7 Scheme III rotor blade back cavitation area

图8 方案1动叶叶背(R=300 mm)汽蚀面积Fig.8 Scheme I rotor blade back cavitation area (R=300 mm)

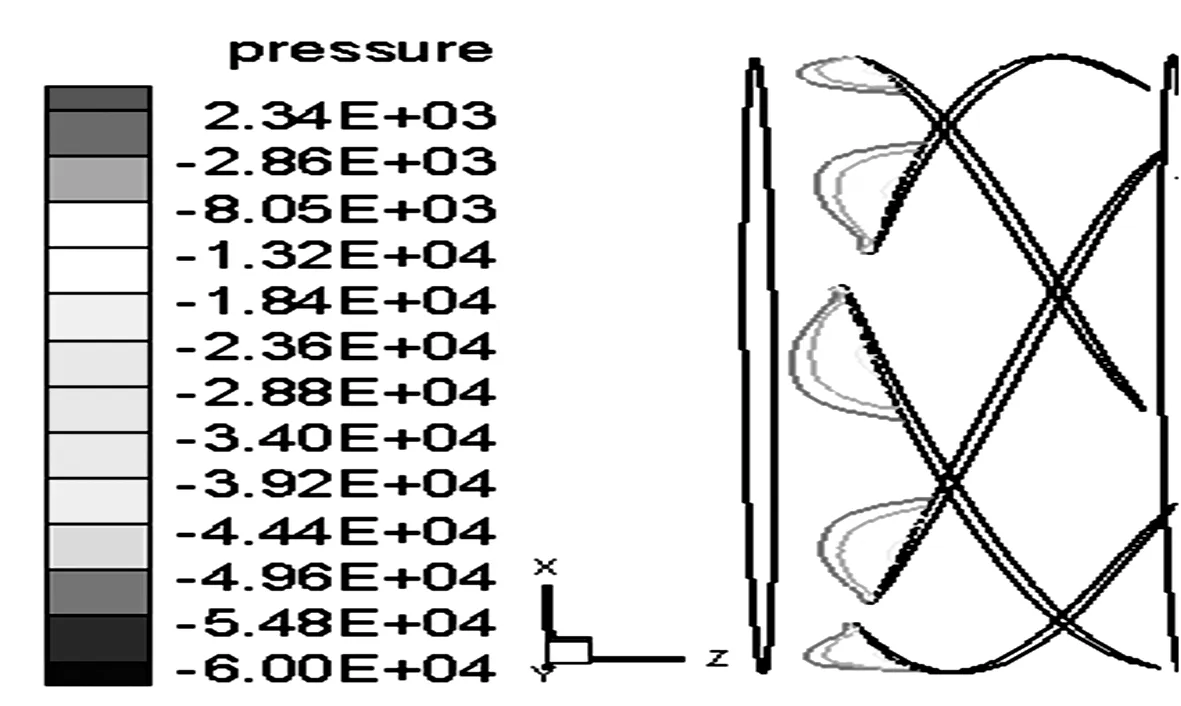
图9 方案2 动叶叶背(R=300 mm)汽蚀面积Fig.9 Scheme II rotor blade back cavitation area (R=300 mm)

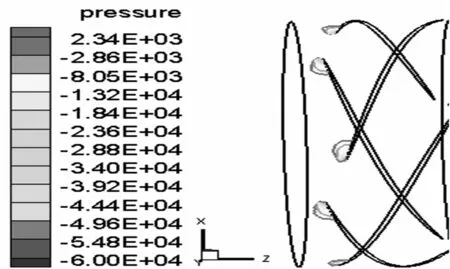
图10 方案3 动叶叶背(R=300 mm)汽蚀面积Fig.10 Scheme III rotor blade back cavitation area (R=300 mm)

图11给出了3种方案在不同径向R截面上的汽蚀面积A对比曲线.显然,3种方案所设计的叶片中,抗汽蚀性差别比较明显.方案3进口处采取一定的抗汽蚀措施,降低了叶片头部的负荷,使得叶片进口处的低压易汽蚀区面积减少,而且由于沿整个叶身负荷分布均匀,因此抗汽蚀能力最好.

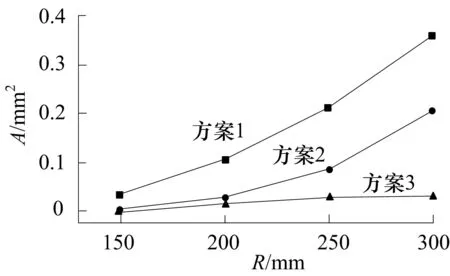
图11 径向截面上的汽蚀面积曲线Fig.11 Curve of cavitation area at different radius

5 结论

1)控制速度矩分布可以改变叶片的负荷分布;

2)控制叶片速度矩vθr的分布,对叶片的形状、外特性及抗汽蚀性能有重要影响;

3)研究结果表明负荷沿轴面流线均匀分布且在叶片头部减轻负荷分布,即可保证高的效率,又具有比较好的抗汽蚀性.

[1] Pellpne C,Peallat J M.Norrlinear analysis of three-dimensional partially cavitating hydrofoil [C]∥ProcoftheInter-nationalSymposiumonCavitationinaCentrifugalPump.Deauville,France:[s.n.],1995,31(3):78-83.

[2] Hirschi R.Leading edge cavitation in a centrifugal pump: Numerical prediction compared with model tests,Hydraulic Machinery and cavitation[C]∥Proceof18thIAHRSymposiumonHydraulicMachinery.[s.L.]:Klu-were Academic Publishers,1996：239-241.

[3] 高忠信.混流式叶轮的准三维S2流面有限元设计方法[J].水利学报,1992(4):63-69.

Gao Zhongxin.Mixed flow impeller ofS2stream surface of three dimensional finite element design method[J].JournalofHydraulicEngineering,1992(4):63-69.(in Chinese)

[4] 徐宇,吴玉林,刘文俊,等.用两相流模型模拟混流式水轮机内空化流动[J].水力学报，2002(8):57-63.

Xu Yu,Wu Yulin,Liu Wenjun,et al. Simulation of cavitation flow in a francis turbine runner[J].JournalofHydraulicEngineering,2002(8):57-63.(in Chinese)

[5] 黄欢明,高红,杜朝辉.轴流泵叶轮内部流动的数值模拟与实验[J].上海交通大学学报,2009,43(1):124-128.

Huang Huanming,Gao Hong,Du Zhaohui.Numerical simulation and experimental study on flow field in an axial flow pump[J].JournalofShanghaiJiaotongUniversity,2009,43(1):124-128.(in Chinese)

[6] 罗兴琦,梁武科,廖伟丽.水力机械转轮准三维反问题研究与发展[J].西安理工大学学报,1997,13(2):157-162.(in Chinese)

Luo Xingqi,Lang Wuke,Liao Weili,et al.The research and development of quasi three-dimension inverse problem of runners of hydraulic machinery[J].JournalofXianJiaotongUniversity,1997,13(2):157-162(in Chinese)

[7] 蔡佑林,王立祥,张新.混流泵叶轮三元可控速度矩的计[J].流体机械,2005,33(11):13-15.

Cai Youlin,Wang Lixiang,Zhang Xin. Design of 3-D controlled velocity moment for impeller of mixed-flow pump[J].FluidMachinery,2005,33(11);13-15(in Chinese)

[8] 曹树良,梁莉,祝宝山,等.高比转速混流泵叶轮设计方法[J].江苏大学学报:自然科学版,2005,26(3):185-188.(in Chinese)

Cao Shuiliang,Liang Li,Zhu Baoshan,et al. Design method for impeller of high specific speed mixed-flow pump[J].JournalofJiangsuUniversity:NaturalScienceEdition,2005,26(3):185-188.(in Chinese)