孔隙尺寸离散度大的碳纤维增强复合材料随机孔隙建模方法研究

梁向雨， 林 莉， 陈 军， 丁珊珊， 李喜孟

(大连理工大学 无损检测研究所，辽宁 大连116024)

建立能够客观描述含孔隙复合材料的物理模型，是进行复合材料性能预测、孔隙率无损检测与评价等工作的前提。但真实孔隙形貌十分复杂，具有明显的随机性和不确定性，尺寸变化范围很大，形状不规则、边界粗糙，从数学和物理角度都很难处理［1］。借鉴地震勘测、储层预测研究中针对复杂地质结构中非均匀性的分析思路和方法［2］，本课题组在国内外首次提出了将随机介质理论和统计学方法应用于含孔隙复合材料研究的学术思想。随机介质是针对非均匀介质提出的统计学描述方法，它由大、小两种尺度的非均匀性所组成。大尺度非均匀性描述介质的平均特性，而小尺度非均匀性是加在上述平均值上的随机扰动［2］。基于随机介质理论，可以将含孔隙复合材料看作是纤维和树脂基体构成的大尺度背景介质上局部随机叠加了小尺度的扰动，这种扰动具有非均匀性特点，以此思路针对碳纤维增强复合材料建立了二维随机孔隙模型(Random Void Model，RVM)［3～7］。研究表明，与基于含孔隙各向同性均匀介质弹性理论的Martin［8］模型相比，RVM 对孔隙的模拟结果与实际孔隙非常相似，为随后采用数值计算方法计算超声参量提供了重要的模型基础。

然而用此方法针对大量微小孔隙中夹杂有大尺寸孔隙的复合材料进行建模时，由于建模参数来自于该孔隙率下所有孔隙观测尺寸的平均值，导致模拟结果中的孔隙尺寸只在较小的范围内变化，尺寸较大的孔隙并未得到体现，使得模拟结果与实际孔隙形貌相差较大。基于此问题，针对孔隙尺寸跨度较大的两组碳纤维复合材料试样，采取依据孔隙尺寸进行分级建模，然后进行叠加处理的方法，完成了含有孔隙尺寸离散度大的复合材料孔隙模型的建立，经与未分级建模结果以及金相观测结果比较，验证了该方法的有效性。

1 原理

随机介质是用于描述非均匀连续介质的统计学方法。在二维随机介质中，点(x，z)处的弹性参量M(x，z)(密度、拉梅常数等)可分解为［9］:

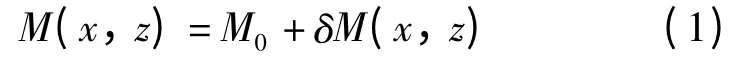
式中，M0为大尺度非均匀性参数，假设为常数或随二维空间坐标(x，z)缓慢变化;x，z 分别为二维直角坐标系的水平与垂直方向坐标;δ 和M 为小尺度非均匀扰动量，并假设其为具有零均值、一定方差及某一自相关函数的空间平稳随机过程。图1a 为采用高斯型自相关函数，自相关长度a =10μm，b=10μm 生成的随机介质。虽然随机介质很好地描述了大小两种尺度上的非均匀性，但连续的随机介质并不适合造成复合材料弹性突变的孔隙型缺陷［2］。采用极值搜索法对随机介质进行改造，可以得到随机孔隙模型［3］。图1b 为孔隙率P =1%的随机孔隙模型，可以看出，生成孔隙的形状、尺寸及分布具有随机性和不确定性，与实际碳纤维增强复合材料中孔隙的形貌及分布特征相似，适于描述含孔隙复合材料。孔隙率P 和自相关长度a，b 共同决定了RVM 中孔隙的形貌特征，自相关长度a，b 取决于金相法对孔隙尺寸进行观测和统计得到的结果。

图1 随机介质和随机孔隙模型 (a)高斯型随机介质(a=10μm，b=10μm);(b)随机孔隙模型(P=1%)Fig.1 Random medium and random void model (a)Gaussian random medium(a=10μm，b=10μm);(b)Random void model (P=1%)

2 实验

本实验所选样品A，B 均采用预浸热压成型方法制备而成的碳纤维增强复合材料板，碳纤维型号为T700，所选树脂类型为环氧树脂，样品厚度为3.7mm。将试样研磨抛光后，借助金相显微镜进行孔隙形貌观察，结果如图2 所示。

利用图像分析软件进行孔隙率和孔隙尺寸的统计。设孔隙截面横向尺寸为长度，用L 表示，纵向尺寸为宽度，用W 表示(如图2b 所示)，然后将两样品中的孔隙按照孔隙长度L 进行分级:A 样品，L ＜50μm 的孔隙为1 级，L≥50μm 的孔隙为2 级;B 样品中，L ＜ 50μm 的孔隙为1 级，长度为50 ≤L ＜200μm 的孔隙为2 级，L≥200μm 的孔隙为3 级。分别统计两样品中各级孔隙的孔隙率和孔隙尺寸，统计结果如表1 所示。可以看出不同级别尺寸的孔隙对于整体孔隙率的贡献权重。

图2 样品A(a)及B(b)中的孔隙形貌Fig.2 The micrographs of samples A (a)and B (b)

3 结果与讨论

针对上述两种样品，分别用未分级和分级两种方法建立随机孔隙模型。其中，未分级建模以所有孔隙的平均尺寸为依据选取自相关长度，直接建立模型;分级建模则以各级孔隙的平均尺寸为依据，分别选取自相关长度建立模型，再将各级别孔隙的模型进行叠加。自相关长度的选取如表2 所示。

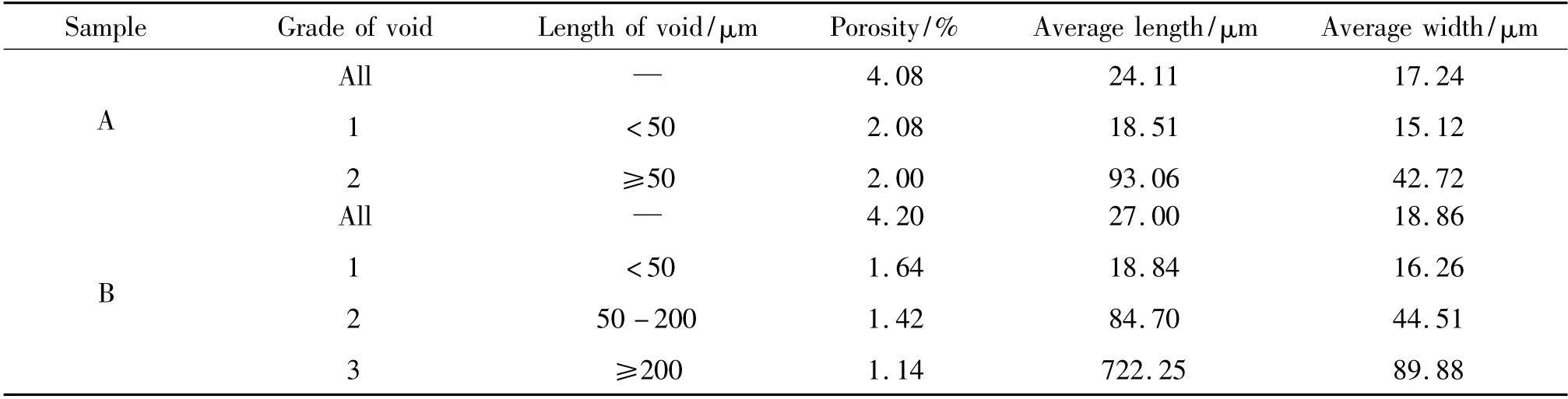
表1 样品A、B 孔隙率和孔隙尺寸统计结果Table 1 The statistical results of porosity and void size for sample A and B

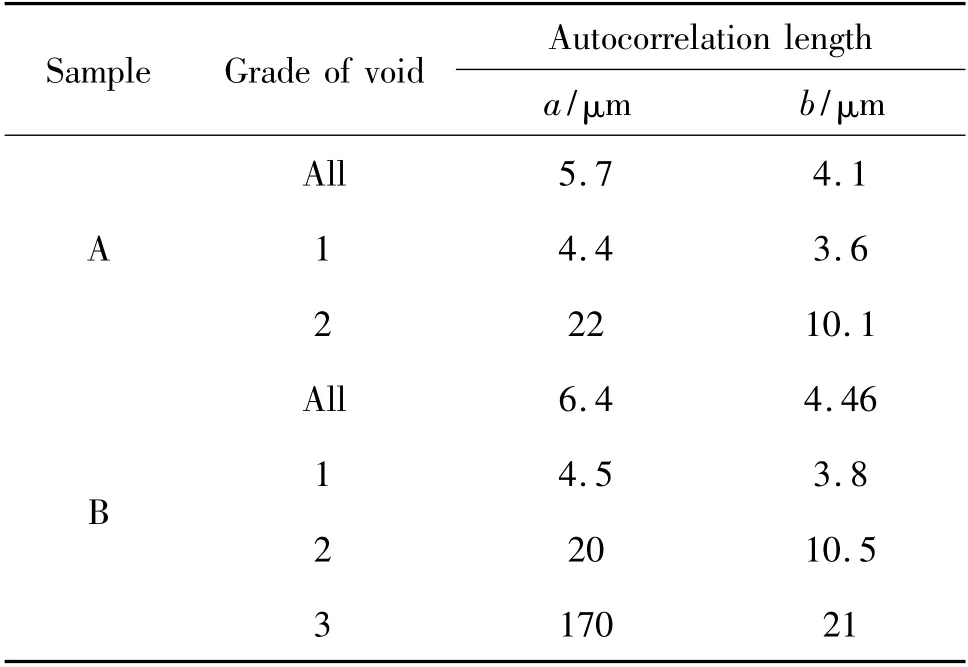
表2 自相关长度的选取Table 2 The determination of autocorrelation length

图3、图4 分别为样品A，B 用两种建模方法得到的模拟结果与实际孔隙形貌的对比。可以看出，由于样品中所含微小孔隙数量过多，孔隙的平均尺寸偏小，以所有孔隙的平均尺寸为依据选取自相关长度建模，导致模拟结果中大孔的丢失。未分级建模结果(图3e、图4f)中尺寸较大的孔隙未能得到体现。而先分级后叠加的建模方法，但模拟结果叠加结果中各个级别尺寸的孔隙均能得到体现，大大改善了模拟结果(图3c、图4d)与实际孔隙形貌(图3d、图4e)之间的几何相似度。由于叠加过程中孔隙相互重叠，会造成孔隙率减小，A、B 的模拟结果的孔隙率分别为4.05%和4.14%，与金相法测得的孔隙率比较，分别减少了0.03%和0.06%，可以看出孔隙率变化不大，并且被覆盖的一般为小孔隙，影响不大。

图3 样品A 分级建模与未分级建模结果比较 (a)1 级孔隙模型;(b)2 级孔隙模型;(c)1，2 级孔隙模型叠加结果;(d)实际孔隙形貌;(e)未分级建模结果Fig.3 The comparisons between the models of sample A with grading and without grading(a)model for voids of grade 1;(b)model for voids of grade 2;(c)superposed result of(a)and (b);(d)the micrograph of sample A;(e)modeling result without grading

图4 样品B 分级建模与未分级建模结果比较 (a)1 级孔隙模型;(b)2 级孔隙模型;(c)3 级孔隙模型;(d)1，2，3 级孔隙模型叠加结果;(e)实际孔隙形貌;(f)未分级建模结果Fig.4 The comparisons between the models of sample B with grading and without grading (a)model for voids of grade 1;(b)model for voids of grade 2;(c)model for voids of grade 3;(d)superposed result of (a)，(b)and (c);(e)the micrograph of sample B;(f)modeling result without grading

4 结论

针对含有孔隙尺寸离散度大的碳纤维增强复合材料，提出了按孔隙尺寸进行分级建模，然后予以叠加的研究思路，避免了随机孔隙模型中大孔的丢失，模拟结果与实际孔隙形貌之间有更高的几何相似度，提高了随机孔隙模型的适用性，为后续研究工作提供了模型基础。

［1］林莉，张翔，陈军，等. 基于随机介质理论的复合材料孔隙二维形貌几何仿真［J］. 失效分析与预防，2010，5(4):204 －209.(LIN L，ZHANG X，CHEN J，et al. Geometric simulation of 2-D morphology of voids in composites based on the random medium model［J］. Failure Analysis and Prevention，2010，5(4):204 －209. )

［2］奚先，姚姚，顾汉民. 随机溶洞介质模型的构造［J］.华中科技大学学报:自然科学版，2005，33(9):105 －108.(XI X，YAO Y，GU H M. Simulations of random cave medium model［J］. Journal of Huazhong University of Science and Technology:Natural Science Edition，2005，33(9):105 －108.)

［3］牟云飞，张翔，林莉，等. 基于随机孔隙模型的CFRP孔隙率超声检测研究［J］. 机械工程学报，2010，46(4):22 －26.(MU Y F，ZHANG X ，LIN L，et al. Investigations on CFRP porosity by using ultrasonic testing based on random pores model［J］. Chinese Journal of Mechanical Engineering，2010，46(4):22 －26.)

［4］LIN L，ZHANG X，CHEN J. A novel random void model and its application in predicting void content of composites based on ultrasonic attenuation coefficient ［J］. Applied Physics A:Materials Science ＆ Processing，2011，103(4):1153 －1157.

［5］LIN L，CHEN J，ZHANG X. A novel 2-D random void model and its application in ultrasonically determined void content for composite materials［J］. NDT ＆ E International，2011，44(3):254 －260.

［6］张翔，陈军，林莉，等. 复合材料孔隙形貌特征对超声波散射衰减影响的分析［J］. 中国机械工程，2010，21(14):1735 －1741.(ZHANG X，CHEN J，LIN L，et al. Effects on ultrasonic scattering attenuation coefficient of morphological characteristics of voids in composite materials［J］. China Mechanical Engineering，2010，21(14):1735 －1741.)

［7］张翔，林莉，陈军，等. 基于确定性和随机性原理的复合材料二维孔隙模型比较［J］. 航空材料学报，2010，30(6):93 －97.(ZHANG X，LIN L，CHEN J，et al. Comparison between 2-D deterministic model and random model of voids in composite materials ［J］. Journal of Aeronautical Materials，2010，30(6):93 －97.)

［8］MARTIN B G. Ultrasonic wave propagation in fiber reinforced solids containing voids ［J］. Journal of Applied Physics，1977，48(8):3368 －3369.

［9］IKELLE L T，YUNG S K，DAUBE F. 2-D random media with ellipsoidal autocorrelation functions［J］. Geophysics，1993，58(9):1359 －1372.