两种典型铺层玻璃纤维复合材料的拉伸力学行为

曾 智， 李玉龙， 郭亚洲， 陈 煊， 王 雷

(西北工业大学 航空学院，西安710072)

时至今日，玻璃纤维增强复合材料(GFRP)作为一种新型材料在飞行器设计中的应用已越来越广泛。相比于传统航材铝合金，GFRP 具有高比强度、高比刚度、低热膨胀系数等一系列优异性能。而相对于碳纤维等其他复合材料，GFRP 价格低廉且具有更好的吸能特性与良好的韧性。GFRP 的增强减重效果明显，常被用来制成次承力部件，如垂尾、壁板等。考虑到飞机结构常常受到冲击载荷的影响，GFRP 的应变率效应、破坏模式和吸能效果已成为重点研究对象［1］。Staab 和Gilat［2，3］利用电子试验机和SHTB 系统研究不同铺层的GFRP 力学性能，发现纤维和基体都是应变率敏感。在10－3～102s－1应变率下，Mahmood 等［4］观察到GFRP 的拉伸极限强度随应变率变大而显著增加，弹性模量和失效应变也有轻微的增加。Bai 等［5］发现了同样的结果。Saniee［6］和Ochola［7］等通过实验得到GFRP 模量和强度都随应变率增加而增加，但失效应变随应变率增加而变小。Okoli 和Smith［8，9］研究过GFRP 在冲击载荷下的破坏模式，结果得到拉伸强度、模量和失效应变、吸收能量分别增加52%，12%，10% 和53%。Renu［10］证实了GFRP 随着应变率的增加，破坏模式会从纤维脆性断裂和纤维大量拔出变成基体失效的整体脆性断裂。Mouhmid［11］用SEM 扫描了铭牌号为PA66 的GFRP 试样断口，认为破坏是从纤维断裂开始，发展到基体开裂，最后发生分层破坏。但是也有研究者发现GFRP 应变率不敏感。Hayes和Adams［12］发现GFRP 在冲击速率为2.7 ～4.9m/s时，弹性模量和强度应变率不敏感。Daniel 和Liber［13，14］设置实验应变率为10－4～27s－1时，GFRP的模量和失效强度表现不敏感。

国内也有一些研究者对GFRP 的力学性能进行过研究［15～18］，但是涉及动态力学性能的研究很少。有学者认为GFRP 属于应变率敏感材料，拉伸时存在着应变率效应门槛值，其值介于20 ～100s－1之间［19，20］。应变率低于门槛值，强化效应便不明显;应变率高于门槛值，材料便表现出应变率强化效应。文献［12～14］中并没有观测到应变率强化效应，可能原因是实验应变率在应变率效应门槛值之下。

本研究以一类玻璃纤维增强复合材料S4C9-1200/SY14 两种典型铺层层合板为研究对象，通过电子万能试验机和分离式Hopkinson 拉杆研究了在10－3～103s－1应变率下材料的拉伸力学性能。从应力应变曲线和试样破坏断口分析了材料的应变率效应、纤维损伤和界面脱粘损伤。在高应变率实验的基础上，验证了应变率强化门槛，明显地观察到材料的强化效应，拟合得出材料的应变率强化门槛值。

1 材料与试样

本工作所用的玻璃纤维增强复合材料铭牌号为S4C9-1200/SY14，该材料为单向玻璃纤维增强复合材料。设计的实验件有两种形式的铺层:［0］16，［±45］4S。实验件制备和实验过程依照ASTM D 3039和ASTM D 6641 标准。

动态实验中所采用的试样均为哑铃形状，标距段长16mm、宽3.5mm、厚2mm。试样如图1 所示。

图1 动态试样Fig.1 Specimen for dynamic uniaxial tension experiments

准静态实验中所采用的拉伸试样均为长度250mm、宽度25mm、厚度2mm 的板形试样，试样的两端分别加有长50mm、宽25mm、厚2mm 的加强片，试样如图2 所示。

图2 准静态拉伸试样Fig.2 Specimen for quasi-static uniaxial tension experiments

2 实验方法

动态下的材料力学性能测试在西北工业大学冲击动力学实验室进行，图3 是实验室中直径为14.1mm的分离式Hopkinson 拉杆系统示意图。分离式Hopkinson 拉杆是通过调节气炮气压及使用不同长度的子弹来实现不同应变率的加载。实验基于一维弹性波理论［21］，通过波形采集器采集弹性杆上的入射、反射及透射应变波εI，εR，εT，利用公式(1)计算出试样中的应力σS，应变εS及应变率˙εS。

式中:E，Ab分别是弹性杆的弹性模量和横截面积;lS，AS分别是试样的原始长度和横截面积;C0是弹性杆中的应力波速。

动态拉伸时，采用国产环氧树脂胶DG-3S 将试样夹持段粘接在杆端凹槽之内，固化24 h。在动态实验时需要注意的是，由于Hopkinson 拉杆中保证实验结果有效性的一个重要条件是加载过程中试样两端的力要达到平衡［22］，而对于复合材料这类脆性材料，其破坏应变较小，往往在未达到平衡时就可能遭到破坏。为实现试样破坏前的力的平衡和近似的恒应变率加载，实验时采用薄橡胶片作为波形整形器［23］。

准静态实验在CSS-88000 系列电子万能试验机上进行。［0］16层板进行了单次准静态拉伸加载。［±45］4S层板进行了准静态拉伸加载-卸载循环实验，实验设计五段循环曲线，第一段应处于弹性阶段，第二段应高于屈服应力，此后每段递增，以达到连续加载-卸载的目的。实验时控制应变率分别为10－3s－1和10－2s－1。

图3 分离式Hopkison 拉杆系统Fig.3 Scheme of the split Hopkinson tension bar

3 实验结果

图4 为单向纤维［0］16层合板的准静态拉伸应力应变曲线，图5 为单向纤维［0］16层板的动态拉伸应力应变曲线。图6 为［±45］4S层板的拉伸加载卸载应力应变曲线。图7 为［±45］4S层板在动态下应力应变曲线。

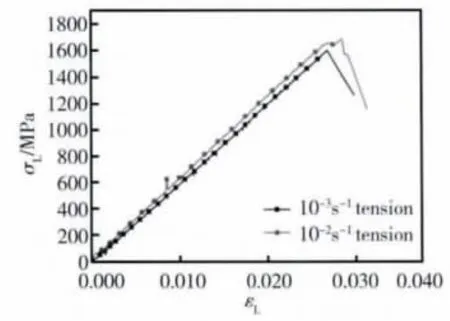
图4 [0]16的准静态拉伸应力应变曲线Fig.4 The stress-strain curves of [0]16 laminates from quasi-static experiments

图5 动态拉伸[0]16应力应变曲线Fig.5 The stress-strain curves of [0]16 laminates from dynamic experiments

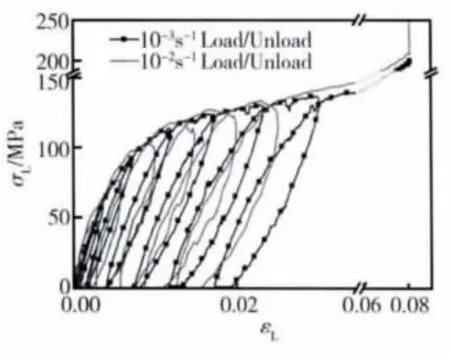
图6 [±45]4s准静态拉伸应力应变曲线Fig.6 Thestress-strain curves of [±45]4s laminates from quasi-static experiments

图7 ［±45］4S动态拉伸应力应变曲线Fig.7 The stress-strain curves of［±45］4S laminates from dynamic experiments

4 讨论与分析

4.1 ［0］16层板的损伤、破坏与强化

纤维纵向拉伸时，Ladeveze［24］等人引入损伤因子df用来描述纤维的拉伸损伤，损伤变量的范围取0≤df≤1。由于纤维破坏前表现为线弹性，df=0;纤维破坏后，df=1。纤维损伤破坏必定有一门槛值和极限值，引入纤维方向的应变表示纤维的拉伸损伤门槛应变，表示对应的纤维拉伸极限应变。以纤维方向的应变εf定义df，将纤维方向的破坏分为三个阶段。当纵向应变小于门槛值时，纤维没有损伤;当纵向应变大于极限值时，纤维损伤取最大值，即。而纵向应变介于门槛值与极限值之间时，纤维的损伤呈现线性增长。

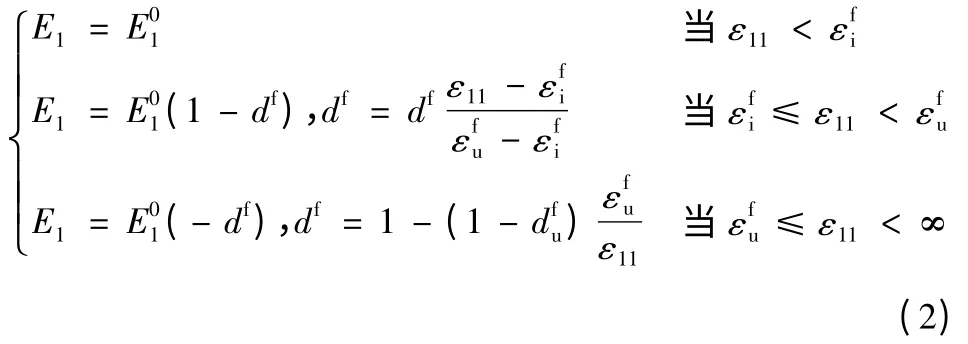
损伤因子与应变的关系如图8 中理论模型所示:

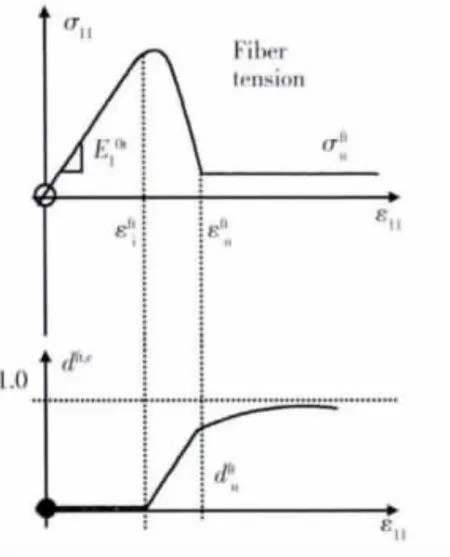
图8 纤维拉伸损伤发展趋势［27］Fig.8 Damage evolution under tension along fiber direction

材料的拉伸损伤门槛应变和极限应变由实验测定。应变率为10－3s－1时，损伤门槛应变和极限应变分别为2.39%，2.68%;应变率为10－2s－1时，其值分别为2.68%，2.74%。将所得数值代入公式(2)，纤维的损伤就和应变直接联系起来。

图4 曲线表明0 度铺层试样失效之前应力应变表现为线弹性关系，破坏时为瞬间失效。10－3s－1应变率下拉伸的极限强度为1596MPa，失效应变为0.0269，弹性模量为59.3GPa;10－2s－1应变率下拉伸极限强度、失效应变和弹性模量分别为1683MPa，0.0286 和62.2GPa，较10－3s－1应变率下分别提高了5%，6%和4.8%。

图9 为［0］16层合板准静态下拉伸破坏后的照片，图9a 所示为10－3s－1应变率下拉伸破坏的试样，图9b 所示为10－2s－1应变率下拉伸破坏的试样。试样表现为劈裂形式的不规则破坏，纤维相互之间成散射状。不同的是10－2s－1应变率下纤维的劈裂散射程度明显较10－3s－1应变率下大，这表明应变率提高，纤维吸收的能量增加了，破坏方式更加剧烈。0 度单层板的失效模式一般分为三种:脆性破坏、带纤维拔出的脆性破坏和处于中间状态的不规则破坏。图9 说明了0 度层合板试样的破坏形式属于不规则破坏。其原因解释为两个方面。轴向拉伸加载时，首先在纤维与纤维间的基体中产生大量微裂纹。纤维达到极限断裂应变时，最薄弱处的纤维随机产生断裂。一方面，随机产生的纤维断裂会引起邻近纤维的应力集中，改变其他纤维的应力场，使得其他纤维失效，从而造成纤维脆性破坏失效［25］。另一方面，由于基体和界面承载能力弱，纤维的断裂会引起裂纹沿纤维间传播。纤维之间的微裂纹吸收能量彼此汇聚连接，造成纤维束的劈裂与散射，导致破坏后纤维间成散射状。当提高应变率时，试样基体中会产生更多的彼此并不联通的微裂纹。轴向加载到纤维的极限应变时，纤维断裂，这些裂纹会迅速沿纤维方向发展，吸收更多的能量，造成更为猛烈的纤维劈裂和散射。所以图9b 的破坏方式比图9a 更为剧烈。

这些实验现象表明了材料在相对较高的应变率下具有更剧烈地破坏方式和更好的吸能效果。［0］16层板动态试样被用来验证纤维的应变率强化效应，应力应变曲线和失效方式如图5、图10 所示。但是纤维间的基体剪切强度远远低于纤维的拉伸强度，试样在拉伸破坏之前已经表现为纤维间剪切破坏。但是在剪切破坏之前，由试样上的应变片得出的应力应变曲线还是有效的。纤维在应变率为151s－1，200 s－1，270 s－1，360 s－1和450 s－1都表现出了极强的应变率依赖性，如图11 所示。取相同应变时，随着应变率的升高，应力变大。

图9 [0]16准静态拉伸破坏照片Fig.9 The fractured spectimen of [0]16 laminates at quasi-static tension （a）10-3s-1；（b）10-2s-1

图10 [0]16动态拉伸破坏照片Fig.10 The fractured specimen of [0]16 laminates at dy-namic tension

强化效应表明纤维拉伸强化存在一个门槛应变率，文献［24，27］认为门槛应变率为100s－1。

图11 不同拉伸应变率下各应变对应的应力值Fig.11 Strain vs stress at the different tension strain rates

4.2 ［±45］4S层板的损伤、破坏与强化

图6 的准静态应力应变曲线显示，在100MPa下，材料卸载仍回到原点，并不产生残留塑性应变。100MPa 后，材料的每次卸载都会产生新的塑性应变。每个循环中的加载曲线直到前一循环应力水平时几乎都是线性的，然后变成非线性，这表明:只有载荷超过前面一次循环的最大应力时才会形成新的损伤，低于这一水平，材料中的裂纹只是宽度变大，不会有较大的扩展或延伸，材料表现为线弹性行为［26］。图中加载–卸载循环曲线的外围轮廓线就是典型的单次拉伸曲线，在低应变率10－2s－1和10－3s－1下表现一致。图中曲线迟滞回环的宽度随着应力的增大而变宽，表明材料在加载过程中存在较大的滑移，且跟应力成正比。而且应变率为10－2s－1时迟滞回环的宽度比应变率为10－3s－1时的大，这表明应变率为10－2s－1时滑移更剧烈些。在这种情况下可以利用每个加载–卸载迟滞回环割线模量的变化，来评价材料在这一应力水平下的性能衰变，这样在拉伸载荷下材料纤维与基体脱粘的损伤演变可以用损伤因子d12来表征:

图12 为［±45］4S层板在拉伸载荷下损伤因子d12与应力的关系曲线，可以看出:材料的脱粘损伤随着剪应力的增大接近于线性发展。应力水平达到纤维与基体脱粘门槛后，损伤线性发展至破坏。应变率为10－3s－1，剪切强度大于30MPa 时，材料开始产生损伤。应变率为10－2s－1时，界面脱粘损伤强度门槛为25MPa。应变率提高一个量级时，界面脱粘损伤强度门槛有所降低。同一剪切应力状态下，相对较高的应变率会在材料中产生更高的损伤。而当界面脱粘开始产生损伤之后，产生相同的损伤时，较高的应变率需要更大的应力增幅。这种趋势反映了材料的应变率强化效应。

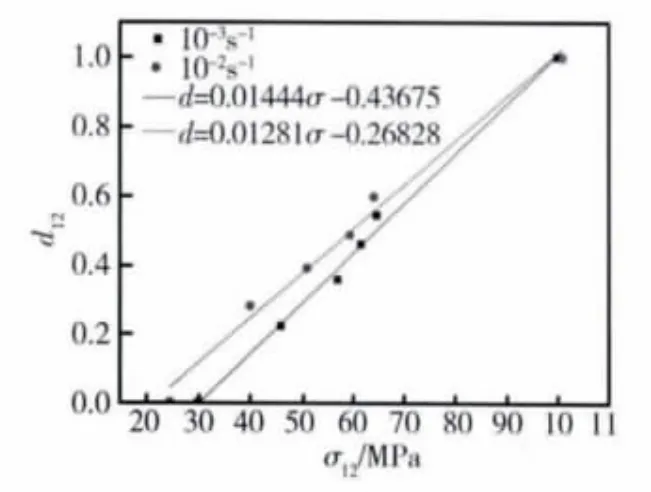
图12 准静态拉伸载荷下损伤因子d12发展趋势Fig.12 Evolution of damage variable d12 in quasi-static tension experiment

图13 极限强度与应变率的关系Fig.13 Variation of failure strength as a function of strain rate

图7 为［±45］4S层板在动态下应力应变曲线。随着应变率的增加，材料的极限强度有明显的提高。图13 为［±45］4S层板的极限强度与应变率之间的关系，图示趋势说明了［±45］4S层板的应变率强化效应。低应变率下材料的极限强度基本保持不变，而动态时，材料的极限强度得到了很大的强化。应变率 为10－3s－1，10－2s－1时，极 限 强 度 分 别 为201MPa，205MPa。相比于10－3s－1，660s－1下极限强度为231MPa，提高14.9%。970s－1和1220s－1下分别为276.5MPa，305MPa，提高37.6%，51.7%。

为量化考察极限强度的应变率依赖性影响，设定参考应变率˙ε0=1s－1，利用以下关系式拟合极限强度σ 与应变率˙ε 的关系［27］:

一般说来σ0的值设定为材料蠕变的极限强度，取值为200MPa。拟合曲线如图13 所示，拟合曲线与实验数值吻合的较好。参数值的取值为a =1.37×10－6，b=1.82。

拟合曲线显示，材料应存在应变率强化门槛。拟合曲线两条切线的交点定义为应变率强化门槛，得门槛值为500s－1。即应变率高于500s－1时，材料有明显的强化效应。

图14 ［±45］4S准静态拉伸破坏照片Fig.14 The fractured specimen of［±45］4S laminates at quasi-static tension

图15 ［±45］4S层板动态拉伸破坏照片Fig.15 The fractured specimen of［±45］4S laminates at dynamic tension

图14、图15 分别为［±45］4S层板在准静态下和动态下的破坏形貌。准静态下试样破坏后，断口呈现类似于燕尾状的破坏特征，但是有着明显的不对称分布。铺层的纤维没有发生断裂，属于界面脱粘，纤维束从基体中拉脱而出。动态破坏下的试样断口均呈现90°燕尾状破坏特征，具有明显的对称性，断口的纤维束显得更加整齐。

4.3 ［0］16与［±45］4S的比较

［0］16层板和［±45］4S层板由于纤维铺层不同，性能存在着很大的差别。轴向承载时，［0］16层板承载能力能达到1600MPa，而［± 45］4S层板只有200MPa，但［±45］4S层板流动应力段较长，失效应变大大提高。纵向拉伸时，［0］16层板损伤为纤维损伤，破坏呈不规则形状。［±45］4S层板的损伤方式是界面脱粘损伤，随着应变率的提高，破坏形状趋向于对称的燕尾形。［0］16层板和［±45］4S层板都有应变率强化效应，且存在应变率强化门槛。［0］16层板的强化效应取决于纤维，应变率强化门槛为100s－1，［±45］4S层板应变率强化门槛值为500s－1。

5 结论

(1)本实验利用电子万能试验机和分离式Hopkinson 拉杆测得了两种典型铺层顺序的玻璃纤维增强复合材料的准静态拉伸、动态拉伸应力应变曲线。

(2)［0］16层板轴向承载能力很强，破坏时表现出典型的不规则脆性破坏，动态强化效应表明纤维强化存在一个门槛应变率，其值为100s－1。

(3)［±45］4S层板主要破坏方式是界面脱粘，纤维与基体的脱粘损伤发展近似线性。同时［±45］4S层板表现出极强的应变率依赖性，应变率强化门槛为500s－1。相比于应变率为10－3s－1时的极限强度，660s－1，970s－1，1220s－1下 极 限 强 度 分 别 提 高14.9%，37.6%和51.7%。

［1］JACOB G C，STARBUCK J M，FELLERS J F. Strain rate effects on the mechanical properties of polymer composite materials［J］.Applied polymer，2004(94):296 －301.

［2］STAAB G H，GILAT A.High strain rate response of angleply glass/epoxy laminates［J］. J Compos Mater，1995，29(10):1308 －1320.

［3］STAAB G H，GILAT A.High strain rate characterization of angle-ply glass/epoxy laminates:proceedings of the 9th international conference on composite materials［C］//ICCM IX，Madrid，Spain，1993(5):278 －285.

［4］SHOKRIEH M M，OMIDI M J. Tension behavior of unidirectional glass/epoxy composites under different strain rates［J］.Composite structures，2009(88):595 －601.

［5］BAI S L，CAO K，CHEN J K，LIU Z D.Tensile properties of rigid glass bead/hdpe composites ［J］. Polymer Compos，2000，8(6):413 －418.

［6］SANIEE F F，MAJZOOBI G H，BAHRAMI M. An experimental study on the behavior of glass/epoxy composite at low strain rates［J］.Journal of Materials Processing Technology，2005 (162):39 －45.

［7］OCHOLA R O，MARCUS K，NURICK G N，et al. Mechanical behavior of glass and carbon fiber reinforced composites at varying strain rates ［J］. Composite Structures，2004 (63):455 －467.

［8］OKOLI O I.The effects of strain rate and failure modes on the failure energy of fiber reinforced composites［J］.Journal of Composite structure，2001 (54):299 －303.

［9］OKOLI O I，SMITH G F. Failure modes of fiber reinforced composites:the effect of strain rate and fiber content［J］.Journal of Materials Science，1998 (33):5415 －5422.

［10］DALAI R P. An assessment of mechanical behavior of fibrous polymeric composites under different loading speeds at above-and sub-ambient temperatures ［D］. Rourkela:National Institute of Technology，2010.

［11］MOUHMID B，IMAD A，BENSEDDIQ N，et al. A study of the mechanical behavior of a glass fiber reinforced polyamide 6.6:experimental investigation［J］. Polymer Testing，2006 (25):544 －552.

［12］HAYES S V，ADAMS D F. Rate sensitive tensile impact properties of fully and partially loaded unidirectional composites［J］.J Test Evaluation，1982，10(2):61 －68.

［13］DANIEL I M，LIBER T.Testing of fiber composites at high strain rates:proceedings of the second international conference on composite materials［C］//ICCM II，Toronto，Canada，1978:1003 －1018.

［14］DANIEL I M，LIBER T.Strain rate effects on the mechanical properties of fiber composites［R］.Report NASA CR－135087，Part 3，1976.

［15］熊杰，王家俊，施楣梧，等.高聚物纤维材料的高应变率响应行为研究［J］. 高分子材料科学与工程，2002，18(5):143 －153.(XIONG J，WANG J J，SHI M W. The high strain rate properties of fiber materials ［J］. Polymer Materials Science and Engineering，2002，18(5):143 －153.)

［16］詹茂盛，孙言丽. 玻璃纤维/嵌段共聚聚酰亚胺复合材料力学性能的研究［J］.塑料，2006(6):1 －5.(ZHAN M S，SUN Y L.Mechanical properties of glass fiber reinforced block － copolyimide composites ［J］. Plastics，2006 (6):1 －5.)

［17］韦玮，程光旭.玻璃纤维增强环氧树脂单向复合材料的研究［J］.西安交通大学学报，1999，33(8):108 －110.(WEI W，CHENG G X.Investigation of unidirectional glass fiber reinforced epoxy resin composite［J］.Journal of Xi'an JiaoTong University，1999，33(8):108 －110.)

［18］夏源明，王兴，杨报昌. 单向玻璃纤维增强环氧树脂在冲击拉伸时的一维本构方程［J］. 复合材料学报，1994，11(4):110 －116.(XIA Y M，WANG X，YANG B C.One dimensional constitutive epuationon of unidirectional glass fiber reinforced epoxy under tensile impact［J］. Acta Materiea Compositea Sinica，1994，11(4):110 －116.)

［19］PETRINIC N. High strain rate mechanical properties of glare［R］.CRAHVI Deliverable Report D1.1.8，University of Oxford，UK，September 2002.

［20］MACARTHY M，XIAO J，PETRINIC N，et al. Modelling of bird strike on an aircraft wing leading edge made from fibre metal laminates part 1:material modeling［J］. Appl Compos Mater 2004，11(5):295 －315.

［21］KOLSKY H. An investigation of the mechanical properties of materials at very high rates of loading ［J］. Proc Phys Soc B，1949(62):676 －700.

［22］郭伟国，李玉龙，索涛. 应力波基础简明教程［M］. 西安:西北工业大学出版社，2007.

［23］CHEN X，LI Y L.Dynamic tensile behavior of two－dimensional carbon fiber reinforced silicon carbide matrix composites ［J］. Materials Science and Engineering (A)，2011，528:6998 －7004.

［24］LADEVEZE P，LE DANTEC E，Damage modelling of the element ply for laminated composites［J］.Composites Science and Technology，1992，43:257 －267.

［25］习年生，于志成，陶春虎. 纤维增强复合材料的损伤特征及失效分析方法［J］.航空材料学报，2000，20(2):55－63.(XI N S，YU Z C，TAO C H. Damage characterization and failure analysis in fiber reinforced composites［J］.Journal of Aeronautical Materials，2000，20(2):55 －63.)

［26］梅辉，成来飞，张立同，等.2 维C/SiC 复合材料的拉伸损伤演变过程和微观结构特征［J］.硅酸盐学报，2007，35(2):137 －143.(MEI H，CHENG L F，ZHANG L T，et al. Damage evolution and micro-structural characterization of a cross-woven C/SiC composite under tensile loading［J］. Journal of the Chinese Ceramic Society，2007，35(2):137 －143.)