具有3-部极小公平划分的树

孙德荣

（昌吉学院数学系 新疆 昌吉 831100）

1 引言

本文考虑的都是简单无向图.通常用A=A(G)表示图G邻接矩阵，如果图G有n个顶点，V={v1,v2,…,vn} 表示图G的顶点集.如果 π=(C1,C2,…,Ck)是顶点集 V（G）的一个剖分,即V(G)=C1⋃C2⋃…⋃Ck,且Ci⋂Cj=φ(i≠j,1≤i,j≤k)，这里Ci称为划分π的一个单元.对任意v∈Ci(1≤i≤k)，用NCj(v)={u∈Cj|uv∈E(G)}表示v在Cj中的邻点集，如果对Ci(1≤i≤k)中的任意顶点v，dij(v)=|NCj(v)|是常数（Cj中的点对Ci中的任意顶点v的度的贡献）,则称π=(C1,C2,…,Ck)是图G的一个k-部公平划分,每个图都至少存在一个k-部公平划分，事实上，如果V(G)=(v1,v2,…,vn)是图G的顶点集，那么令Ci={Vi}(1≤i≤n)，显然π=(C1,C2,…,Cn)是图G的n-部公平划分，一般来说，一个图的公平划分是不唯一的，例如，图1

令C1={v1,v5}，C2={v2,v6}，C3={v3,v8}，C4={v4,v7}，容易验证π=(C1,C2,C3,C4)与π′=(C1,C2,C3⋃C4)都是图1的公平划分。图的公平划分在图的结构的研究中有着广泛的应用，我们知道图的特征值是图的不变量，它是刻画图的特征的一个重要指标。如果图G的特征值入对应的某个特征向量的分量和不为零，则入称为图G的主特征值。而图的主特征值是图的闭道数的主要参数，与图的结构有很大的关系,例如，只有一个主特征值的图G一定是正则图（［1］），这类图具有1-部公平划分。Y.Hou和H.Zhou（［2］）找到了所有的恰有两个主特征值的树，分别是：调和树Ta(a≥2)、星S1,n和双星Sn+1,n+1，Y.Hou和F.Tian（［3］）还证明了恰有两个主特征值的所有单圈图是Clk，而这些图除了调和树Ta(a≥2)以外都恰好具有2-部公平划分。孙德荣（［4］-［5］）证明了顶点集具有二部公平划分的图都恰好有两个主特征值，并且通过对某些具有3-部公平划分的树的研究发现，这些树又都恰好有三个主特征值，而Hagos（［6］）证明了一个图G的主特征值的个数m(G)等于G的walk-矩阵W(G)的秩，于是孙德荣（［5］）将Hagos的结论做了进一步推进，利用公平划分将图G的walk-矩阵W(G)进行了简化，给出了关于图的公平划分π的walk-矩阵W(π)并证明了矩阵W(G)的秩=矩阵W(π)的秩=m(G)。本文研究具有3-部公平划分的树的结构特征，并给出所有具有3-部公平划分的树类。

2 具有3-部极小公平划分的树

对于图G的公平划分π=(C1,C2,…,Ck)来说，同一个单元中的点的度是相等的，为叙述方便，我们用d1,d2,…,dk表示相应单元的度序列。

如果π=(C1,C2,…,Ck)是图G的k-部公平划分，而对任意正整数j＜k，G的j-部划分π′=(,,…,)都不是公平划分，那么 π=(C1,C2,…,Ck)称为图G的极小公平划分。

关于图的极小公平划分有以下基本结论

定理2.1设π=(C1,C2,…,Ck)是图G的k-部公平划分，d1,d2,…,dk表示相应单元的度序列，如果d1,d2,…,dk两两不相等，则π一定是图G的极小公平划分。

证明：假设π=(C1,C2,…,Ck)不是图G的极小公平划分,则G就存在另外一个公平划分π′=（,,…,）是它的极小划分,其中j＜k.不妨设,…表示这个极小划分的度序列,由于d1,d2,…,dk和,,…分别表示同一个图的不同划分的度序列，所以对任意dl(1≤i≤k),存在(1≤m≤j)使得dl=dm′.由于d1,d2,…,dk两两不相等,那么…,也应两两不相等,于是k=j,矛盾。证毕

定理2.2设π=(C1,C2,…,Ck)是图G的k-部公平划分，d1,d2,…,dk表示相应单元的度序列。π是图G的极小公平划分的充要条件是：对任意di=dj(i≠j)，至少存在一个单元Cm(1≤m≤k)使得dim(vi)≠djm(vj)(vi∈Ci,vj∈Cj)。

证明：必要性 π=(C1,C2,…,Ck)是图G的极小公平划分,若存在di=dj(i＜j),对任意一个单元Cm(1≤m≤k)都有dim(vi)=djm(vj)(vi∈Ci,vj∈Cj),这样就可以将划分π中的单元Ci与Cj合并成一个单元Ci′=Ci⋃Cj,而其余单元保持不变,于是就得到图G的一个新的公平划分π′=（C1,C2,…,Ci-1,,Ci+1,…CJ-1,CJ+1,…,Ck）,公平划分 π′较 π 少了一个单元,此与 π=(C1,C2,…,Ck)是图G的极小公平划分矛盾。

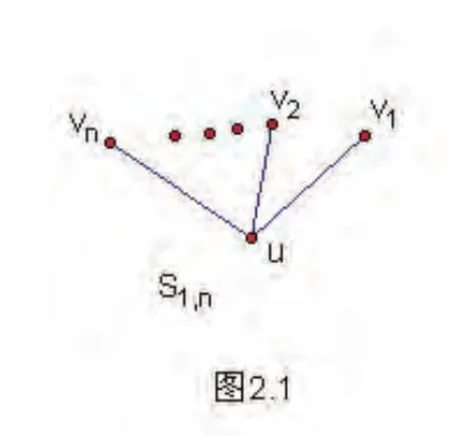
充分性反证法,设π=(C1,C2,…,Ck)是图G的k-部公平划分，d1,d2,…,dk为相应单元的度序列,假设π=(C1,C2,…,Ck)不是图G的极小公平划分,那么另存在图G的一个极小公平划分π′=（,,…,）,使得l＜k,这样就至少存在划分π的两个单元Ci与Cj,当di=dj(i≠j)时,单元Ci与Cj中的顶点同属于π′的某个单元。由于对任意di=dj(i≠j)，至少存在划分π一个单元Cm(1≤m≤k)使得dim(vi)≠djm(vj)(vi∈Ci,vj∈Cj),所以不论Cm(1≤m≤k)中的点属于划分π′的哪一个单元,都不能保证单元中所有的点在划分π′的其它单元中有相同个数的邻点,此与π′是公平划分矛盾。证毕下面构造几个具有3-部极小公平划分的树，由于星图S1,n、双星图Sn+1,n+1分别是具有2-部公平划分的树，在此基础上，可以构造出几类具有3-部公平划分的树。如上图，在星图S1,n（图2.1）的每个叶子上都悬挂k个悬挂点得到的新图（图2.2）记为。显然图是一棵树。

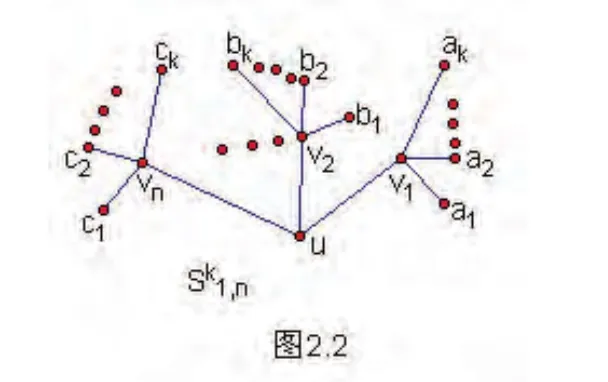
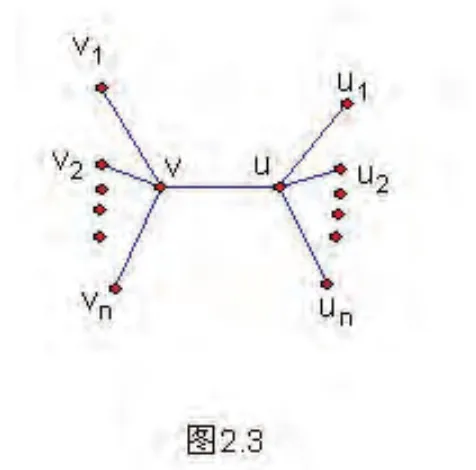
如上图，在双星图Sn+1,n+1（图2.3）的每个悬挂点上都连接k个悬挂点得到的新图（图2.4）记为+1,n+1，显然图+1,n+1是一棵树。

定理2.3树和1,n+1都具有3-部极小公平划分。证明：首先证明树具有3-极小公平划分，如图2.2令C1={a1,a2,…,ak,b1,b2,…,bk,…,c1,c2,…,ck} ，C2={v1,v2,…,vn} ，C3={u} ，由定理2.2知，π=(C1,C2,C3)是图的一个3-部极小公平划分。

其次证明树+1,n+1具有3-极小公平划分，如图2.4，令C1={u,v}，C2={v1,v2,…,vn,u1,u2,…,un} ，C3={a1,a2,…,ak,b1,b2,…,bk,…,c1,c2,…,ck,e1,e2,…,ek,f1,f2,…,fk,…,g1,g2,…,gk}，由定理2.2知 ，π=(C1,C2,C3)是图1,n+1的一个3-部极小公平划分。证毕

3 主要结果及证明

定理3.1T是一棵具有3-部极小公平划分π=(C1,C2,C3)的树当且仅当T=或Skn+1,n+1.

为了证明定理3.1下面给出几个引理：

引理3.2T是一棵具有3-部极小公平划分π=(C1,C2,C3)的树，则T的叶子一定全部含在同一个单元中。

证明：假设有两个以上的单元含有叶子，不妨设C1与C2中都有叶子，那么由公平划分得知：同一个单元中的点的度是相等的，所以C1与C2中只能有叶子，此时如果C1与C2中的点相邻（或C1与C2都是自身相邻），那么C1、C2都与C3不相邻，这样树T就不连通，矛盾。所以，T的叶子只能全部含在同一个单元中。证毕

引理3.3T是一棵具有3-部极小公平划分π=(C1,C2,C3)的树，对任意单元Ci(i=1,2,3)，如果Ci中没有叶子且与叶子相邻，则Ci中的点自身不相邻。

证明：因为T是一棵具有3-部极小公平划分π=(C1,C2,C3)的树，由引理3.2知T的叶子一定全部含在同一个单元中，不妨设叶子全部含在C3中。假设C3中的点与C2中的点相邻，那么C3中的点与C1中的点就不相邻，如果C2中的点自身相邻,而C2中的点又与C1中的点相邻,于是对∀v∈C2,就有d(v)≥3。这样从树T上删去所有的叶子C3得到的树没有叶子,矛盾。因此C2中的点自身不相邻,证毕

引理3.4T是一棵具有3-部极小公平划分π=(C1,C2,C3)的树，对任意单元Ci(i=1,2,3)，如果Ci中的点自身相邻，则Ci中至多有两个点。

证明：T是一棵具有3-部极小公平划分π=(C1,C2,C3)的树，不妨假设C1中的点自身相邻，由引理3.2知，C1中没有叶子，而且叶子全部含在同一个单元中，不妨设叶子全部含在C3中，由引理3.3知，C3只能与C2相邻。由树的连通性可知C2既与C3相邻又与C1相邻，现在删去树T上所有的叶子（C3中的点）得到的是树T-C3，由于π=(C1,C2,C3)是树T的极小公平划分，所以树T-C3具有2-部公平划分φ=（C1,C2），根据引理3.3，在树T-C3中，C2中的点全部是叶子。再从T-C3中删去所有的叶子（C2中的点）得到的是树T-C3-C2,这棵树只剩下C1中的点，由于π=(C1,C2,C3)是树T的极小公平划分，所以树T-C3-C2是正则的，要么是一个点，要么是一条边，所以C1中至多有两个点。证毕

定理3.1 的证明：充分性在定理2.3中已得证，下面证明必要性。设T是一棵具有3-部极小公平划分π=(C1,C2,C3)的树，由引理3.2不妨设叶子全部含在C3中且C3中的叶子与C2中的点相邻，那么由引理3.3知C2中的点自身不相邻，由树的连通性知C2中的点必与C1中的点相邻，根据引理3.4，C1中至多有两个点，有两种情况：当C1中只有一个点时，C2中的所有点必与C1中的一个点相邻，此时T-C3就是一个星图，所以T=；当C1中有两个点时，由公平划分知C1中的每个点与C2中相同个数的点相邻，此时T-C3就是一个双星图，所以T=1,n+1。证毕

文献[5]证明了所有的树T=（n≠k2+k+1）、Skn+1,n+1恰有三个主特征值，结合定理3.1树的3-部公平划分与其主特征值的关系就非常清楚了。

［1］Cvetkovic D.M.The main part of the spectrum,divisors and switching of graphs,Publ.Inst.Math.（Beograd）1978,23（37）：31-38.

［2］侯耀平，周后卿.恰有两个主特征值的树［J］.湖南师范大学自然科学学报，2005,28（2）：1-3.

［3］HOU Yao Ping,TIAN Feng.Unicyclic graphs with exactly two main eigenvalues,Appl.Math.Lett.19（2006）：1143-1147.

［4］孙德荣，黄琼湘.恰有两个主特征值的图与图的剖分［J］.应用数学学报,2012,35（2）：252-262.

［5］孙德荣，徐兰.恰有三个主特征值的树［J］.山东大学学报理科版,2013,48（2）：252-262.

［6］Hagos E.M.Some results on graph spectra,Linear Appl.2002,356：103-111.