硼氮富勒烯图的反强迫数

蒋晓艳,程晓胜

(惠州学院 数学系，广东 惠州 516007)

0 引言

图G的一个独立边集叫做G的一个匹配。G的完美匹配(凯库勒结构)M是一个匹配且G的每个点都与M中的一条边相关联。若G的边集S满足G-S有唯一完美匹配，则称S为反强迫集。包含边数最少的反强迫集叫做极小反强迫集，其边的数目叫做图G的反强迫数，记作af(G) .

本文主要考虑硼氮富勒烯图，它是硼氮富勒烯的分子图。实际上，硼氮富勒烯图是一个 3-连通，3-正则的平面图，它的面要么是四边形要么是六边形，所以硼氮富勒烯图是二部图，并且根据欧拉公式，可以计算出它恰好有六个四边形。

在第二部分，首先我们得到一类管状，环边连通度为3的硼氮富勒烯图Tn的反强迫数为2(n+2) .然后，我们讨论任何硼氮富勒烯图的反强迫数不少于 3，并构造出所有反强迫数为 3 的图，共包含两个。

1 硼氮富勒烯图的反强迫数

我们用Tn记一类管状硼氮富勒烯图，其中它包含n个同心六角形层(即每一层是由三个六角形构成的环链)，再在两头分别冠上一个由三个四边形构成的帽子，例如图1中给出的是T2.值得注意的是在Tn的画法中，最外边的三条悬挂边实际上关联着同一个点。作为退化情况n=0,Tn，就是通常所指的立方体。记T:={Tn;n>0} .

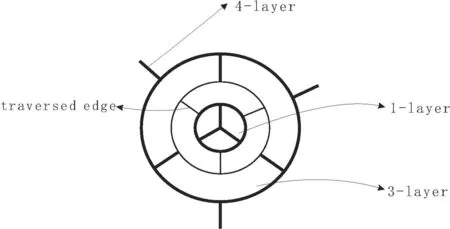
图1 T中的例子T2，及其层和横跨边的示意图

为了方便，根据Tn的同心层，我们给出它的一个分解。定义1-层是由位于一端的三个四边形构成的帽子，第2-层是由与第一层相邻的三个六边形构成的环链并去掉在1-层上度为3的三个点。两个同心6-长圈(非面圈，即不是某个面的边界)之间的边叫横跨边。用相同的方法我们可以定义第i-层(2≤i≤n+1) 。第(n+1)-层是Tn另一端帽子上的一个爪子(即中心一个点关联这三条边)。在每个i-层，三条横跨边形成一个匹配，在1-层和(n+2) -层三条横跨边分别与中心点关联，例如见图1.

Tn的完美匹配有以下特点：

引理1[3]设M是Tn的任一完美匹配，那么M恰好包含每一层的一条横跨边。相反，任何一个恰好包含每一层一条横跨边的边集都能扩充为Tn的唯一完美匹配。

引理2[3]设H是二部图G的一个导出子图，M0是H的完美匹配，且M0能扩充为G的完美匹配M。如果G-H有至多一个 1-度点，那么M0的任一子集都不是M的强迫集。

下面我们给出Tn的反强迫数。

定理1 若Tn∈T，则af(Tn)=2(n+2) .

证明 设S是Tn的最小强迫集，我们断言则|S|≥2(n+2) 。利用反证法，假设|S|<2(n+2) 。首先对于Tn的每一层至多有两条横跨边在S中，否则，Tn将被分成两个分支，且每个分支有奇数个点，则Tn-S中没有完美匹配，与S是反强迫集矛盾。由鸽笼原理知，至少有一层至多含有一条边。不失一般性，假设是i-层，那么i-层中有两条横跨边不在S中。而对于剩余的每一层，存在一条横跨边不在S中。现在我们选择i-层的任从i-层中任选一条不在S中的横跨边，从剩余每一层中选不在S中的横跨边作为匹配边，根据由引理1，我们得到两个不包含S中边的完美匹配，这与S是反强迫集矛盾，所以 |S|≥2(n+2).另外，我们可以找到一个大小恰为 2(n+2) 的反强迫集S0：对于i-层(1≤i≤n+2 ),任选两条横跨边放在构成S0中，则由引理1 知，Tn-S0有唯一完美匹配，且|S|=2(n+2) .由此定理得证。

对于任意硼氮富勒烯图，我们给出其反强迫数的下界：

定理2 若G为任一硼氮富勒烯图，则af(G)≥3.

证明 设S是G的反强迫集。反证，假设|S|≤ 2，那么G-S至多有一个1-度点，由引理2 知，G-S不止有一个完美匹配，矛盾，所以af(G)≥3.

以下我们构造出所有反强迫数达到下界的的硼氮富勒烯图。

定理3 设硼氮富勒烯图G，如果af(G)=3 ，那么G同构于B4N4或者B6N6.

证明 设G的大小为 3 的反强迫集为S={e1,e2,e3}.M为G-S的完美匹配。下面我们给出S的结构。

断言.S中没有独立边，即不与S中其它两条边关联的边。

反证，若不是，不失一般性，假设有一条独立边e1，则在G-S中至多有一个 1-度点，此点同时与e2,e3相关联。由定理 2.2 知，G-S至少有两个完美匹配，矛盾。

因此，S中的边情形有两种。首先，e1,e2和e3关联同一个点，这样G-S中就会有孤立点，矛盾。第二种情况，e1,e2和e3是一条3-长路上的三条边。不妨设这条路为ae1be2ce3d，在G-S中恰好有两个1-度点b和c，则边bb1和cc1在M中。设H是由a,b,b1,c,c1,d导出的子图，在G-S中，只有当点a和点c1相邻，点d和b1点 相邻时，才能产生两个 1-度点a和d，否则G-S中没有1-度点。如此边aa1和边dd1在M中。设H1是由点集V(H)∪{a1,d1} 所导出的子图。如果在G-H1中没有其它点，则连接边a1，b1,c1，d1,a1,d1就会得到图B4N4,见图2 (a)。

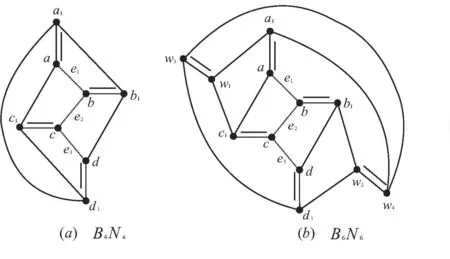
图2 定理证明示意图

若还有其它点，只有当点w1与点a1，c1相邻，w2与点b1，d1相邻时为 1-度点，那么边w1w3和w2w4在M中。由硼氮富勒烯图的定义，则一定有边连结点w3和点w4，否则将产生 2-边割。至此我们得到B6N6，见图2 (b)。

参考文献:

[3]Jiang X Y,Zhang H P. On forcing matching number of Boron-nitrogen fullerene graphs[J].Discrete Appl Math, 2011, 159:1581～1593.