透空管防波堤上的波浪力

傅朝方 ，朱大同

(1.东南大学华宁交通监理咨询公司,南京 210018; 2.东南大学东南交通监理咨询公司,南京 210018)

我国海岸线漫长，各地的海况和地形地质条件差异极大，因此沿岸和离岸的海港工程建设和海岸防护需要建造各种类型的防浪与消波结构。1982年候国本[1]提出的管式防波堤方案是-个有创意的构想，在工程上得到应用。这类透空结构的特点：1)能防护波浪对港口和岸坡的冲击；2)能透流、保持港内水体循环，维护水质环境[1-4]；3)结构形式很简单，单体重量可以做的较轻，占用的予制场地不大，可以利用小型起重工具施工；4)消波机理非常复杂。自这类透空结构问世后，仅李春柱等[5-6]对管式防波堤的反射系数和波浪力展开了全面、深入的理论和模型试验研究，得到了一组计算反射系数与波浪力公式。受李春柱等[5-6]的启发，本研究在对管式防波堤非线性水动力学边界条件分析基础上，用阻抗分析法提出-组计算波浪反射和传递系数严格的公式。此外，在此基础上进-步讨论波浪反射和传递系数公式以及波浪力计算的近似公式，将近似公式的计算结果与侯国本[1]和李春柱[5]的试验和朱大同[4]理论计算数据做对照，近似公式与实验及严格理论计算符合较好。同时计算其中所有参数事先已经知道，不必通过室内模拟试验测定，因此特别适合于初步设计阶段和中小型港口使用。

1 透空管防波堤上的波浪反射和传递系数的近似公式

计算图式和坐标轴取法与李春柱等[5]相同。透空管防波堤由若干个宽度B，高度2h，中间开有宽B1和高2h1矩形孔的矩形管平行迭置而成，其管长(即透空堤厚度)为D。坐标轴放在静水面上，原点在堤前沿x轴指向来波方向，z轴垂直向上(图1)。水深d、波高H和周期T的推进波正向入射到堤面上。设定透空堤厚度为D与波长相比是一个很小的量。

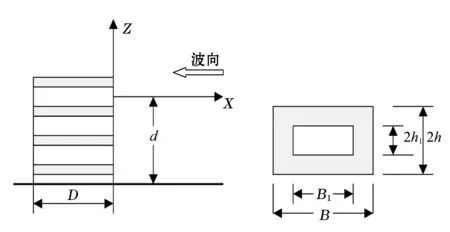
图1 透空管海堤Fig.1 A sketch map of perforated-pipe breakater

本研究将总的流场分为两个子域：迎海面域(x≥0)和背海面域(x≤0)。

1.1 迎海面域中入射波与反射波的势函数

法向入射波(波向与-x轴平行)与反射波迭加后波场的速度势为

[ejkx+Re-jkx]ejωt

(1)

式中,k为波数；g为重力加速度；ω为波圆频率；R为反射系数。水质点速度及波动压力分别表示为

[ejkx-Re-jkx]ejωt

(2)

p1=jωρΦi(i=1,2)

(3)

按照阻抗分析法[3]，由式(2)和(3)可得迎海面域内合成波场的波阻抗为

(4)

式中,ρ为水的密度；c为波速；ρ，c两者的乘积称为特性阻抗。从式(4)中可以清楚的看到，迎海面外海域中入射波与反射波迭加之后的波阻抗是坐标的函数。在透空管防波堤前缘(x=0)处，合成波的阻抗(也称海域的负载阻抗)为

(5)

1.2 港池内波的势函数

通过透空管在港池内传递波的势函数为

[Tejk(D+x)]ejωt

(6)

式中,T为传递系数。波压力同式(3)，采用与上面相同的推导过程，得港池内的波阻抗为

(7)

1.3 波浪通过透空管的流阻分析

水流通过透空管的流动,与许多透空堤，如桩列堤，开孔板防波堤相似，在工程现场和模型试验都可观察到：障壁(桩列，格栅开孔板和透空管等)的前缘(迎海面)与后缘(港池内)水位是不连续的。这部分水头(压力)损失源于克服水流通过隔壁的线性和非线性阻力。正确分析和表达这部分内容，是解析透空管防波堤消波机理和水动力特征的关键。

透空管内的流体受到3个方面的作用：(1)流体在透空管内往复振动的惯性力；(2)流体流经透空管内表面的粘性阻力；(3)流体流入透空管内突然收缩与流出透空管时的突然扩张的阻力。流体总力可表示为

(8)

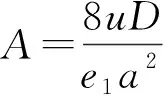
(9)

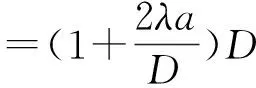
式(8)内右端第2项AV，除以体积速度Vd获得波浪通过透空管线性流阻为

(10)

式中，ν是运动粘性系数，ν=-μ/p。

式(8)右端第3项bV2是非线性阻力项，除以Vd获得透空管两端压力下降(或水头损失)Δp=(ζo+ζi)ρV2,非线性流阻为

(11)

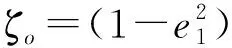
(12)

波浪在克服这些阻力时消耗了能量，从而达到降低反射波和削减波浪作用力的结果。式(8)中第一项是感抗部分，它不消耗能量，但可以在坐标平面内平移反射和传递系数曲线的位置。

当波浪通过透空管时，总的波阻抗Zpc为

(13)

式 (13)中右端括号中第一项,相当于梅强中公式内与射流长度相关的项，黄振华[7]用管长D与开孔率e1之比表示，但对管长未做修正。显然在本研究中导出该项的物理意义非常明确。

根据阻抗连续原理，透空管前缘迎海面上阻抗式(13)，必然等于外海合成波场在透空管迎海面处的阻抗式(5)。令

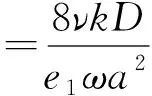
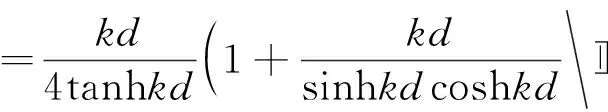
(14)

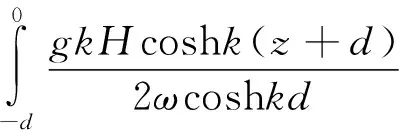
(15)

透空管防波堤的能量耗散系数E，可以直接表为

E=1-(R2+T2)

(16)

2 透空管防波堤上波压力和波浪力公式

2.1 透空管防波堤迎海面上波压力和波浪力

将式(1) 和反射系数R代入式(3)，得迎海区域内任一点上波压力公式为

(17)

当x=0时，得到防波堤迎海面上任一点波压力为

(18)

将式(18) 沿水深积分，得防波堤迎海面上单位宽度波浪力为

(19)

2.2 透空管防波堤背海面上波压力和波浪力

将式(6) 和传递系数T代入式(3) ，得到背海面上任一点波压力公式x=-D

(20)

将式(20) 沿水深积分，得防波堤背海面上单位宽度波浪力为

(21)

作用在透空管防波堤上单位宽度纯波浪力为

ΔF=|F1|-|F2|

(22)

3 对比验证与分析

解析公式(14)，(15)和(18)～(22)，对于海况条件和结构几何参数已经确定的透空管防波堤，用波浪反射和传递系数的解析公式(14)、(15)和波浪荷载计算公式(18)～(22)做设计，计算需用的数据已齐全，没有待定或需要从模型试验反算的参数。而且公式结构十分简单，参数均是现成可查，所以计算工作非常方便。为了说明上述公式的试用性和可靠性，现将它们与前人的试验成果对比。

3.1 波浪反射系数的公式与试验成果对比

将本研究中计算透空管防波堤波浪反射和传递系数的理论公式(14)与李春柱等[5]的试验成果对比。试验条件如下：一根透空管的宽度B=15 cm，高度2h=10 cm；开孔面积为11 cm×6 cm；管长D=26 cm。透空管防波堤的开孔率与一根透空管的开孔率是相同的，即e1=66/150=0.44。利用内表面积相等，换算半径a=5.41 cm。水深d=40 cm，50 cm。波高和周期均采用李春柱等[5]表列数据。

图2 严格和近似的反射系数与试验比较Fig.2 Comparison of calculated values of reflection coefficient with the tested data

图2中，|R|严格值为用朱大同[4]中公式计算获得；|R|近似值为本研究公式(14)计算获得；|R|实验值为李春柱等[5]的试验获取值。结果表明，反射系数计算值与试验吻合较好。对于水深d=50 cm，周期大于2.6 s计算与试验有差别。

3.2 波浪力的公式与试验成果对比

由于李春柱等[6]的实验中没有详细列出模型的几何参数，除了水深之外，本研究在计算中的其余参数均与图2内所用值相同。图3内包含了李春柱等[6]的波浪力试验值和计算值及本研究采用近似公式计算的结果。李春柱等[6]认为，透空管之间存在缝隙等4个因素降低了堤上波浪力的值，使该文中理论值普遍高于试验值。图3表明：波周期短时，本研究结果与李春柱等[6]试验值-致；波周期较长时，大量波能传递到港池，使堤两侧压力差减小。本研究结果低于试验值。

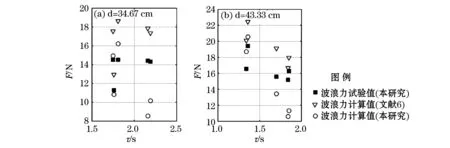
图3 波浪力计算值和试验值的比较Fig.3 Comparison between the tested and the calculated wave forces

现在波浪荷载计算公式(18)～(22)与候国本[1]的波浪力试验结果对比。采用条件如下，水深d=15 m，波高H=5.2 m，时间常数τ=7.6 s。透空管长度(即透空堤厚度)D=8.5 m，透空管半径a=0.5 m。一个单元面积A=5.61 m2，它的透水面积为2.1 m2，所以防波堤的开孔率为e1=0.374 3。从候国本[1]的波浪力试验获得了本研究公式所需要的全部参数资料。 将防波堤迎海面上4个特征点的波压力计算值与候国本[1]的波浪力试验结果列于图4a，本研究的预测与试验吻合很好。防波堤背海面上的波压力计算值列于图4b。

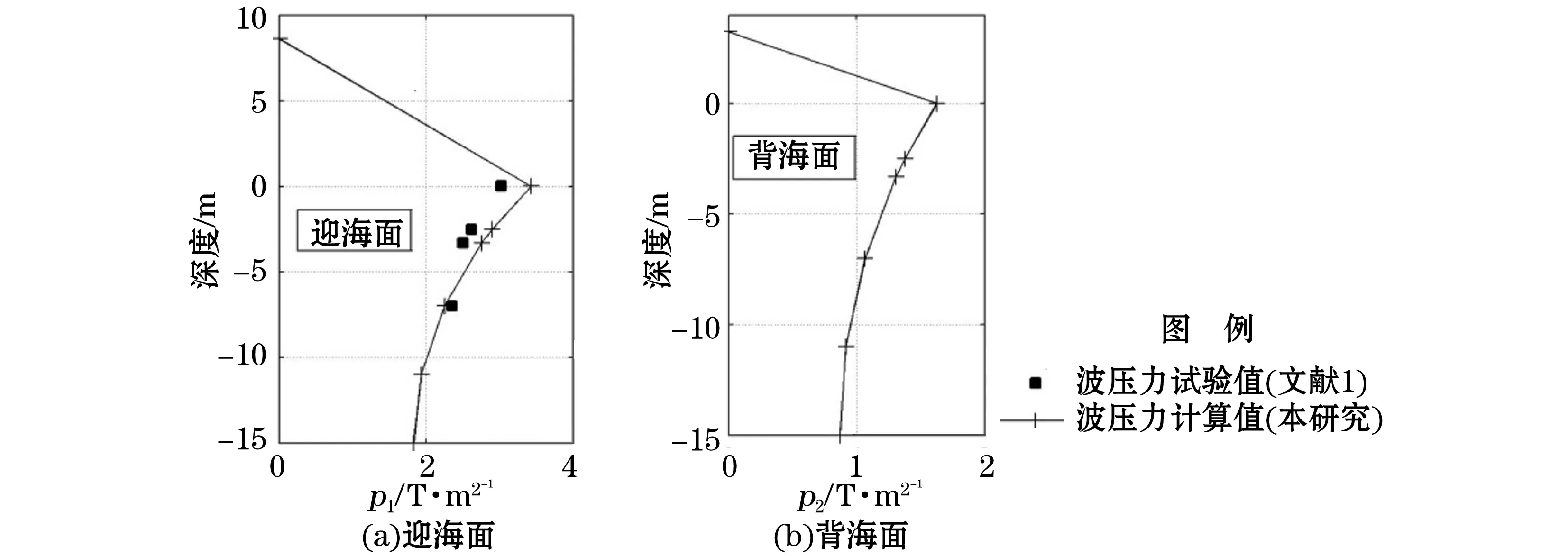
图4 迎海和背海面上波压力Fig.4 Wave pressures both on the seaward side and on the landward side

通过候国本[1]的波浪力试验参数，计算防波堤反射和传递系数，以及波能损失系数随波周期的变化列于图5。图5a曲线的分布与其他型式透空堤有相同的趋势[3]。

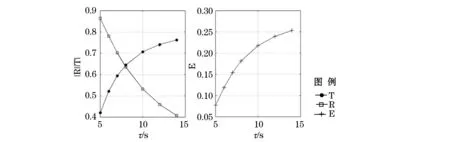
图5 反射系数R和传递系数T以及能量耗散系数E伴随波周期的变化Fig.5 Changes of |R|,|T| and wave energy loss coefficient with the wave periods

由图5b可知，随着波长增加，传递系数增大，透过防波堤的能量也增加，波浪通过防波堤时消耗在流阻上的能量也上升。图6a是防波堤迎海面上波压力随波周期的变化。短周期容易被反射，因此堤前反射系数大，导致作用在迎海面上静止自由表面附近的波压力增大。随着波长增大，越来越多的能量进入港区，堤前反射系数减小，迎海面上的波压力降低。在τ=14 s时，在迎海面上静止自由表面附近的波压力降到最低点。图6b曲线分布规律与图6a正好相反，随着波长增大，越来越多的能量进入港区，背海面上的波压力逐渐升高，到τ=14 s时，背海面上的波压力升至最大值。由图6可知，当τ=14 s时，迎海面上和背海面上静止自由表面附近的波压力大致相等，内外压力基本平衡。

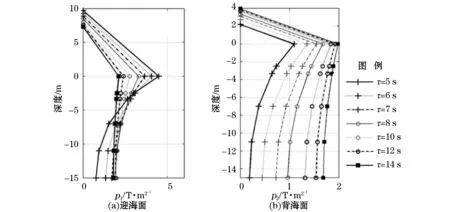
图6 迎和背海面上波压力伴随波周期的变化Fig.6 Changes of wave pressures on the seaward and the landward sides with the wave periods

4 结 论

1)文内导出的堤面反射和传递系数的理论公式(14)、(15)，波压力和波浪力的计算公式(18)～(22)，形式简单、结构严密、计算精度优良，十分便于工程应用。

2)透空管防波堤上波浪的反射和传递特征，与其它透空堤水力特征有相似的分布。透空管防波堤的主要参数，如相对管长、开孔率、周期和波陡，对防波堤的波浪反射系数、传递系数、能量耗散系数以及波压力和波浪力有重要影响。一般，随相对管长和波陡增加，波浪反射系数增大、传递系数和能量耗散系数减小；随周期增加，反射系数减小、传递系数和能量耗散系数增大；随着开孔率增加，传递系数增加、反射系数减小、能量耗散系数也减小。

3)透空管防波堤迎海面上和背海面上的波压力随深度分布有较大的差别。短周期从防波堤上反射的能量多，透过堤的能量少，相应地反射系数大，传递系数小。所以迎海面上波压力大，背海面上小。防波堤上波压力，无论是迎海面还是背海面，都是在静水位处达到最大，随深度增加迎海面上波压力迅速减小。背海面上波压力随深度变化较缓慢。相反，长周期波通过透空管防波堤的能力强，所以迎海面上波压力小，而背海面上波压力增加。这对于主要用在短周期波为主导海域的小型港口是有利的。

4)管式透空防波堤与其它透空堤一样，有较好的应用前景，对它的理论研究和模型试验应得到更广泛的重视。为了提高管式透空防波堤的效率，有更好的经济技术指标，应对它的结构形式做必要的改进，如设法增加阻性等措施。

[1] 候国本.管式透空防波堤试验研究[J].海岸工程,1982,1(1):1-8.

[2] 贾玉成.挡板式高桩码头透浪特性分析[J].海岸工程,2009,28(1):1-8.

[3] 朱大同，博朝方. 桩列透空堤的水动力计算[J]. 海岸工程,2011，30(2):1-6.

[4] 朱大同，博朝方.波浪与透空管防波堤的相互作用[J].水动力学研究与进展:A辑, 2010,25(5):587-593

[5] 李春柱,才毅,魏守林.管式透空防波堤反射系数研究[J].海洋工程,1991,9(4):69-79.

[6] LI C Z, SHI H D, YU D Y, et al. Calculation of wave pressure and pressure spectrum for perforated-pipe breakwater[J]. China Ocean Engineering, l997, 11(1):79-88.

[7] HUANG Z H. Wave interaction with one or two rows of closely spaced rectangular cylinders [J]. Ocean Engineering, Elsevier, 2007,34(11-12):1584-1591.