数据处理中缺失数据填充方法的研究

胡玄子， 陈小雪， 钱叶亮， 姜正龙， 赵彤洲

(武汉工程大学计算机科学与工程学院，湖北 武汉 430073)

在海量信息处理过程中，经常会遇到数据集不完整的情况，通常称之为缺失数据．缺失数据产生的原因很多，例如受客观条件限制导致的信息无法获取，信息因人为疏忽被遗漏，信息属性值不存在等因素．针对这些缺失数据，前人做过很多有益的工作，处理方法大致分成三类：删除、填充、丢弃．删除数据就是将存在确实数据的一组数据完全删除，从而得到的数据是没有确实数据的完整的数据集合．在数据分析中，这种方法与丢弃数据的方法都比较简单，是以牺牲某些记录属性为代价的．但在多维数据处理中，数据的不同属性之间很可能存在某种关系，而完全不考虑存在缺失数据的那些属性，就很可能影响对数据集合的方差及数据分布的准确判断．因此，针对缺失数据填充方法的研究成为人们关注的热点问题．缺失数据的填充方法大致分为两类：基于统计的方法和基于数据挖掘的方法．

统计方法主要通过对数据进行分析，得出数据集的一些统计信息，然后利用这些信息填充缺失数据．根据对数据集的了解程度，统计填充方法可以分为参数方法、非参方法以及半参方法．最常用的参数方法就是线性回归、EM算法．数据挖掘算法主要有贝叶斯方法、神经网络方法、粗糙集规则方法等等[1]．根据数据特点，本文有选择性地对如下四种方法进行了研究．

1 算法分析对比

1.1 拉格朗日插值法

其中ωn+1(x)=(x-x0)(x-x1)…(x-xn),

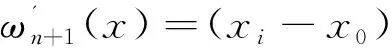
(xi-xi-1)(xi-xi+1)…(xi-xn).

在数据填充时，可以利用已知数据求出拉格朗日插值多项式，然后将待求节点带入该多项式，就可以求出目标值．

1.2 回归分析法

所谓回归就是在已知数据基础上，构建回归模型，找出回归模型中的参数，用以模拟和预测未知数据的过程．常用的线性回归方法，是以误差平方和最小为基本思想，寻找回归参数的过程[2]．本文仅讨论一元线性回归分析．

当求出回归模型的参数后，将缺失点数据x带入回归模型，即可求出填充数据y．

1.3 灰色预测法

灰色预测是通过少量的、不完全的信息建立数学模型，进而找到模型参数的过程．它具有运算方便，建模精度高的特点，在各种预测领域都有着广泛的应用，是处理小样本预测问题的有效工具．定义[3]如下，设给定观测数据列

x(0)={x(0)(1),x(0)(2),…,x(0)(N)}.

经一次累加得到

x(1)={x(1)(1),x(1)(2),…,x(1)(N)}.

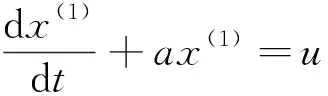
特别地，当t=t0时,x(1)=x(1)(t0)．对等间隔取样的离散值则为

采用最小二乘法来确定a、μ．当模型系数确定后，采用同样的方法，将缺失点带入方程，求得缺失数据的估计值．

1.4 BP神经网络法

BP网络是由已知的输入矢量和输出矢量，训练出一个网络用来逼近某个函数，具有较强的泛化性．主要思想是使网络上的节点真实值与模拟值的误差平方和最小，即用网络的实际输出A1,A2,…,Aq, 与目标矢量T1,T2,…,Tq之间的误差修改其权值，使实际输出值与期望值尽可能接近从而能得到一个训练好的网络[4-6]．在此采用两层BP网络结构．

2 数据填充方法在空气质量数据分析中的应用

自2012年入冬以来，各地出现的雾霾天气不断成为人们关心的话题，也成为各大媒体关注的焦点，武汉市已经实现PM2.5的24小时监测．本实验采集了2013年3月13日至4月29日(晚上8点)的武汉市PM2.5值(表1)．由于各种原因，导致有部分数据缺失．为了得到相对完整的、可靠的数据集，我们采用上述4种方法进行了数据填充的工作，力图寻找一种适用于该类数据填充的方法．在估计未知数据时，为检测算法的有效性，我们将部分已知数据剔除后，进行准确性对比，并同时估计未知数据．

表1采集到的部分PM2.5原始数据μg/m3

日期PM2.5日期PM2.5日期PM2.53/131073/301334/15773/14663/311324/16883/15754/11514/171203/26844/3964/20693/16604/4684/22303/17944/5544/23613/201534/6684/241033/21984/8734/251103/221834/9314/26833/241454/10534/27593/25674/11574/28523/27884/12414/29393/28804/13643/29944/1474

其中，有8天数据缺失．用上述四种方法分别进行了数据填充．为检验算法的有效性，首先将部分已知数据剔除，然后分别用四种方法计算剔除数据的估计值，并与真实值对比，结果见表2、表3．

表2 各种算法对剔除数据的估计值和真实值的对比 μg/m3

表3 各种算法的残差 μg/m3

为定性检验上述算法的准确性，我们对各种算法的后验差比值进行计算并比较．后验差比值的计算方法为

F=s2/s1.

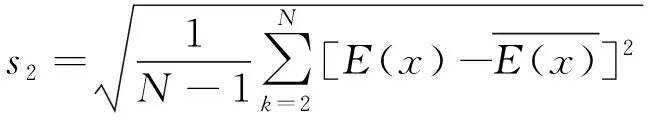
即，s1是x(0)的方差，s2是残差的方差．由此定义可知，后验差比值反映了残差相对于标准偏差偏离的程度，后验差比值越小，表明估计值偏离真实值的程度越小，就越接近真实值．通过上述方法计算各种算法的后验差比值，见表4．从表4中可见，拉格朗日插值法的后验差比值最小．因此模拟效果最好．按照此方法，对缺失数据进行估计，可得估计值见表5．

表4 各种算法后验差比值

表5 缺失数据的估计值 μg/m3

3 结论

尽管填充数据的算法有很多种，但是，并不是每种算法都能适用于所有数据．针对空气质量参数之一的PM2.5的缺失数据填充，我们进行了一些探索性尝试，认为拉格朗日插值法能比较准确填充缺失数据，进而可以实现部分数据的预测．考虑到研究的科学性，这种算法不一定是最好的，随着研究的深入，我们认为还有更好的方法值得探索．

另外，从数据预测的趋势可见，武汉市PM2.5数值在3-4月份呈现下降的趋势．

[参考文献]

[1] 刘星毅，曾春华. 缺失数据的处理和挑战[J].钦州学院学报,2008，23(06)：25-29.

[2] 蒋金山，何春雄，潘少华. 最优化计算方法[M]. 广州：华南理工大学出版社,2008.

[3] 张光澄. 非线性最优化计算方法[M]. 北京：高等教育出版社,2005.

[4] 倪 勤. 最优化方法与程序设计[M]. 北京：科学出版社,2009.

[5] 杨淑莹. 模式识别与智能计算：Matlab技术实现[M].北京： 电子工业出版社,2008.

[6] S Theodoridis. 模式识别[M]. 第4版.北京：电子工业出版社,2010.

[7] 张德丰. MATLAB神经网络应用设计 [M].第二版． 北京：机械工业出版社,2012.

[8] 周建兴. MATLAB从入门到精通[M]. 第二版. 北京：人民邮电出版社,2012.