折流板几何结构对换热器性能影响的数值模拟

龚发云， 叶方平， 汤 亮， 李晓敏

(湖北工业大学机械工程学院， 湖北 武汉 430068)

换热器是化工、炼油、动力、食品、轻工、原子能、制药、航空及其他许多工业部门广泛使用的一种通用工艺设备．在化工厂中，换热器的投资约占总投资的10%～20%；在炼油厂中，该项投资约占总投资的35%～40%．鉴于换热器在工业生产中的重要作用及其能耗大的现状，改进和提高换热器的性能及传热效率成为节能降耗的重要途径[1]．管壳式换热器的综合性能由多个指标构成，换热器壳程中的流动与换热情况相对来说比较复杂，并且壳程内部的流动情况和换热特性对换热器的性能有着直接的影响，相反，换热器列管中的流动规律可用相关的公式进行计算得到，而且其对换热器性能的影响不大，所以需要对换热器壳程中的流动与换热情况进行探究．邓斌[2]等和沈人杰[3]等应用CFD方法对螺旋折流板换热器进行了数值模拟，黄兴华[4]等采用多孔介质模型和合适的分布阻力方法将弓形折流板换热器数值模拟结果与实验结果进行了对比，张少维[5]等将弓形折流板换热器和螺旋折流板换热器的工作特点进行了数值模拟的对比，Ender Ozden[6]等应用CFD方法探讨了单弓形折流板换热器在不同湍流强度下的流动与换热情况．曲面型折流板换热器等新型换热设备虽然有其优点，但是其几何结构复杂增加了机械加工的难度，导致单弓形折流板换热器的使用仍然比较广泛，所以对弓形折流板换热器壳程流动和换热性能方面的研究十分必要．

1 流体流动与传热的控制方程

1.1 质量守恒方程(连续性方程)

质量守恒定律可以表述为：单位时间内流体微元体中质量的增加等于同一时间内流入该微元体的净质量[7]．按照这一定律，可以得出质量守恒方程：

1.2 动量守恒方程

动量守恒方程可表述为:微元体中流体动量对时间的变化率等于外界作用在该微元体上的各种力之和[7]．按照这一定律，可以得出动量守恒方程：

X方向，

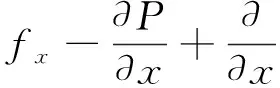
Y方向，

Z方向，

桥梁工程是我国建设工程中的重要组成部分，随着科学技术水平的不断进步，BIM技术作为一种现代化的模型构建技术在桥梁工程施工中发挥了卓越的应用效果。非对称外倾拱桥是一种形式特殊的桥梁，其施工过程难度较大，如何在非对称外倾拱桥的施工过程中对BIM技术进行有效利用，提高工程的施工质量，成为大量研究学者关注的内容。

式中：f为流体单位质量的体积力；μ为流体的动力粘度；λ为流体的第二分子粘度，对于气体可取为λ=-2/3．

1.3 能量守恒方程

能量守恒方程是包含有热交换的流动系统必须满足的基本定律，可表述为：微元体中能量的增加率等于进入微元体的净热流量加上体力与面力对微元体所做的功[7]．按照这一定律，可以得到温度T为变量的能量守恒方程：

式中：Cp为比热容；T为温度；λ为流体的导热系数；ST为粘性耗散项，即流体的内热源及由于粘性作用流体机械能转换为热能的部分[7]．

2 计算模型

2.1 换热器几何结构参数

数值模拟的的单弓形折流板换热器包括4种不同高度的折流板和3种不同的折流板间距．换热器如图1所示．这些换热器的外形尺寸都相同，其中壳体外径为273 mm，壳体长度为1 632 mm，换热管直径为25 mm且都呈正三角形排列，折流板厚度均为6 mm．

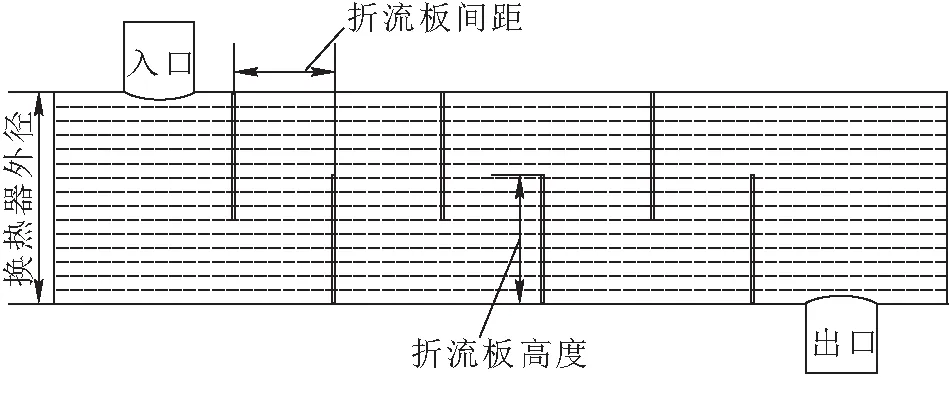
图 1 换热器几何结构图

2.2 数值模拟和边界条件的确定

壳程流体为空气，换热器入口温度为298 K，管程温度为定值378 K．基于不可压缩的牛顿型流体，在常物性和宏观热能守恒的假设下，换热器管程和壳程流体的流动和热量传递必须满足连续性方程、动量守恒方程以及能量守恒方程[8]．

流场使用基于有限体积法的Fluent求解软件进行数值模拟．前处理中的三维几何模型使用正交六面体网格进行划分，数值模拟过程中使用三维单精度求解器，空气入口处为速度入口边界(Velocity-inlet)、空气出口边界条件为Outflow，壁面边界条件设置为无滑移边界(no-slip)、选择基于压力的半隐式求解方式，激活标准k-ε湍流方程、在求解参数的过程中根据模拟的实际问题选择流动方程(Flow)和湍流方程(Turbulence)、湍流耗散率和湍动能方程的离散均采用二阶迎风格式(Second Order Upwind)．由于在Fluent软件中有4种速度-压力耦合算法，在本次模拟过程中采用基于非结构网格的SIMPLE算法．

3 计算结果的分析及讨论

3.1 不同入口速度对换热的影响

在边界设置中将入口速度设置为1 m/s、2 m/s、3 m/s、4 m/s分别计算，得到不同进口速度的温度分布云图(图2)，从图2中可以看出，随着换热器入口速度的增加，折流板之间的高温区域趋于减少，死区面积减少，换热器的有效换热面积得以扩大，从而提高了传热效率．数值模拟中对进口速度设置较小，进口速度与换热量之间是近似线性比例关系(图3)．

图 2 不同速度入口的温度分布云图

图 3 速度与换热量之间的关系

3.2 不同折流板间距对换热的影响

在初始网格建模时分别设计了折流板间距为100 mm、200 mm、400 mm的换热器，其中入口速度设置为1 m/s、2 m/s、3 m/s、4m/s分别计算，得到不同折流板间距入口速度与换热量之间的曲线和不同折流板间距入口速度与压降之间的关系曲线．从图4可以看出，在同一速度的分布上，当入口速度为4 m/s，折流板间距为100 mm时，由于折流板间距的减小，导致换热器的换热量增加幅度趋于20%，随着折流板间距的逐渐减小，换热器的换热量趋于随之增大．

壳程流体流动压降直接影响到动力消耗，是反映换热器性能的重要指标之一[9]．从图5中可以看出，随着折流板间距减小，换热器的压降随之增大，而且折流板换热器压降均随空气入口速度的增加而呈递增趋势．

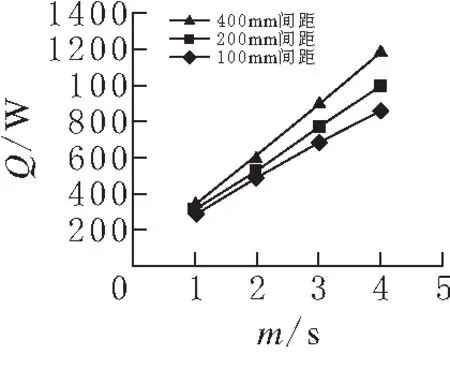
图 4 不同折流板间距入口速度与换热量之间的关系

图 5 不同折流板间距入口速度与压降之间的关系

3.3 不同折流板高度对换热的影响

在计算折流板高度变化对换热器壳程流动与换热过程中，采用折流板间距为200 mm的换热器模型，以折流板高度作为变量，分别取128.5 mm、144.5 mm、160.5 mm、176.5 mm，换热器进口速度取3 m/s(图6)．

图 6 不同折流板高度的温度分布云图

从4个不同折流板高度模型计算的温度场云图可以看出，随着折流板高度的增加，壳程温度降低程度越来越明显，由于流体对换热管壁的冲刷，换热强度有所下降，因此，在换热器壳程中的局部区域出现较低的温度区域．

为了便于显示壳程流体的流动状态，选取了中间对称剖面的速度矢量图(图7)，从所示界面的速度矢量云图可以得出，随着折流板高度的增加，受到折流板的阻挡作用增强，流体流通的主流区域集中于折流板窗口的纵向延伸方向，流体流向改变的位置愈加接近下一个折流板，同时流动死区也逐渐增大，主流区流速大大高于其他区域流速，流速分布的不均匀性更加突出．

图 7 不同折流板高度的速度矢量图

压力损失和传热系数是衡量换热器性能的两个重要指标，但是从优化设计的角度出发，单独通过任何一个参量确定换热器整体性能的优劣显然不可取，目前国内外使用较多的处理方法是以单位压力损失下换热系数的大小作为衡量标准来综合评估换热器的整体性能[9]．

图 8 不同折流板高度与换热量之间的关系

图 9 不同折流板高度的换热性能指标

图9显示，随着折流板高度的增加，换热器性能指标有着明显下降的趋势，尽管图8中曲线显示折流板的几何高度对换热量有明显增大作用，但是由于折流板越高造成的壳程流体压降升高，因此造成换热性能指标下降．

4 结论

1)在同一折流板物理模型中，换热器入口速度的增加会使折流板之后的高温区域减少，换热死区面积的减少，增大换热器的有效换热面积，提高传热效率．在模拟过程中设置的进口速度很小，产生了换热量与进口速度之间近似线性比例的关系．

2)折流板间距越小即折流板数目越多，换热器的换热量趋于随之增大，但是壳程压降却急剧上升．

3)折流板高度升高时，流体流动换向的缺口面积变小，使得换热器的换热量得到增加，但换热器性能指标是下降的．

[参考文献]

[1] 古 新.管壳式换热器数值模拟与斜向流换热器研究[D].郑州：郑州大学图书馆，2006.

[2] 邓 斌，吴 扬，陶文铨.螺旋折流板换热器壳侧流动的数值模拟[J].西安交通大学学报，2004，38(11):1 106-1 109.

[3] 沈人杰.螺旋折流板换热器数值模拟研究[D].西安：西安交通大学，2003.

[4] 黄兴华，王启杰，陆 震.管壳式换热器课程流动和传热的三维数值模拟[J].化工学报，2002，30(07)：15-18.

[5] 张少维，周荣兰，桑芝富.折流板间距对换热器性能影响的数值研究[J].南京工业大学学报，2005，27(03)：65-68.

[6] Ender Ozden，Ilker Tari.Shell side CFD analysis of a small shell-and-tube heat exchanger[J]. Energy Conversion and Management，2010(51):1 004-1 014．

[7] 周俊杰，徐国权,张 华,等.Fluent工程技术与实例分析[M].北京：中国水利水电出版社，2011.

[8] Prithiviraj M，Andrews MJ. Three dimensional numerical simulation of shell- and-tube heat exchangers [J]. Numerical Heat Transfer，1998(33)：799-916.

[9] 乔志晶. 弓形折流板换热器壳程流体流动与传热的数值模拟[D].哈尔滨：哈尔滨工程大学图书馆，2011.