液体静压导轨静态特性的计算
2013-11-12王焱清吴星成
王焱清, 黄 振, 吴星成
(湖北工业大学 机械工程学院, 湖北 武汉 430068)
高端制造装备的进一步发展对决定装备性能的主轴回转主运动系统以及工作台、刀架拖板进给运动系统等关键运动部件的动态性能及其稳定性、可靠性提出了更加苛刻的要求,促进了液体静压支承技术的研究向更加深入的方向发展.静压导轨作为重要的支承部件,其运动精度将直接影响到工件的加工质量.故对静压导轨的设计显得尤为重要,在静压导轨设计与优化中所需考虑的三个典型的静压系统特性是:承载量、刚度和流量.这三个静态静压系统特性的计算是由油腔内的压力分布决定的,与速度无关.所以计算油腔压力分布是计算静态系统特性的基础.
1 液体静压导轨的工作原理及其静态特性
1.1 液体静压导轨的工作原理
由液体静压导轨的结构(图1)可看出液体静压导轨是利用润滑油膜来支承载荷并起润滑作用[1],根据供油方式的不同,可将液体静压导轨分为定量式静压导轨和定压式静压导轨.本文中计算定量供油时的开式静压导轨.
所谓开式静压导轨,是在工作台和导轨面间通入压力油,使运动件浮起,工作在不同速度下都能保证导轨面在液体润滑摩擦状态下工作.
液体静压导轨中各独立的承载部分称作油垫,由油腔、封油边和进油孔组成(图2),计算液体静压导轨静态特性时通常对其中一个油垫进行分析计算.设从供油系统供给一定压力p、流量为Q的润滑油,导轨上的负载大小为W,油膜厚度为h.当导轨运动处于稳定状态时,不同的载荷W对应一个不同的油膜厚度h,当导轨上负载W增大,油膜厚度h会减小,导轨间的液阻增大,但是定量供油的流量不变使得油腔压力升高从而平衡增大的负载;反之,当负载减小时,油膜厚度增大,液阻减小,油腔压力降低,平衡减小的负载[2].
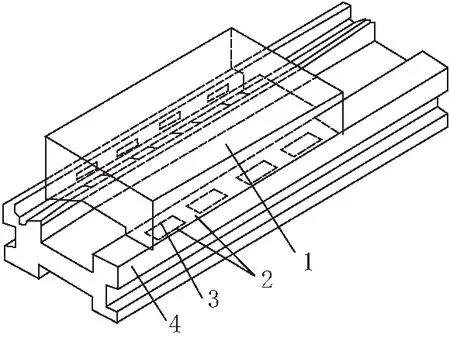
1-工作台; 2-油封面; 3-油腔; 4-导轨座图 1 开式静压导轨

图 2 液体静压导轨中承载部分工作原理
1.2 液体静压导轨的静态特性
1.2.1静承载力W0液体静压导轨的静承载力是表征液体导轨在导轨运动副之间无相对运动时承载力的参数,其值表示在一定油膜厚度下液体导轨的负载能力,可以通过对整个油膜表面的压力积分而得,即
(1)
式中:p为油膜表面的压力分布;A为油膜表面的区域面积.
1.2.2静刚度K0液体静压导轨的静刚度表征液体静压导轨在油膜发生变化时承载力的变化程度,说明了当油膜变化时的承载力的变化情况,其值为
.
(2)
式中:Wh1,Wh2分别是不同油膜厚度时的承载力值;h1,h2分别是两个不同油膜厚度的值.
1.2.3封油边出口流量Q0是表征液体静压导轨在工作时的液体消耗量,常被分为体积流量和质量流量.液体静压导轨的分析中通常用质量流量,液体静压导轨的封油边出口流量可以通过对封油边出口边界区域的液体流速积分得到,即
ρvdA.
(3)
式中:ρ是液体的密度,v是液体出口的流速分布,A是出口边界的区域面积.[3]
2 液体静压导轨油膜压力分布计算方法
2.1 液体静压导轨压力分布
由液体静压导轨静态特性可得,承载能力W0油膜刚度K0都与油膜压力分布有关,要计算承载能力和油膜刚度就必须先计算油膜压力的分布p.
油膜压力的分布p的计算是基于雷诺方程的解,雷诺方程是流体润滑轴承的基础方程,它描述了在微小间隙内流体的压力分布,它的普遍形式是
(4)
式中:x和y分别是指的导轨长度方向和宽度方向的坐标;η是润滑流体粘度;ρ是润滑流体密度;h是油膜厚度;U是导轨运动速度;方程的解p是油膜压力分布.这个椭圆型的偏微分方程仅仅对于特殊的间隙形状才可能求得解析解,而对于复杂的几何形状或工况条件下的润滑问题,无法用解析方法求得精确解.随着电算技术的迅速发展,数值法成为求解润滑问题的有效途径.
2.2 液体静压导轨压力分布数值解法
因为静压轴承的静态特性中承载量、刚度与速度无关,且在静态状态下油膜厚度h不随时间变化.简化式(4)可得在静态下的雷诺方程式:
.
(5)
式(5)是一个Laplace算子,其在油膜分布区域上的解就是压力在油腔中的分布.其数值解法是将偏微分方程转化为代数方程组的变换方法.它的一般原则是:首先将求解区域划分成有限个数的单元,并使得每个单元充分小,以至于可以认为在各单元内的未知量(油膜压力p)相等或者依照线性变化,而不会造成很大的误差.然后通过物理分析和数学变换方法将求解的偏微分方程写成离散形式,即转化为一组线性代数方程组.该方程组表示了各个单元的带球未知量与周围各单元未知量的关系,最后根据Gauss消去或者Gauss-Seidel迭代法求解代数方程组,从而求得整个求解域上的未知量.
静压导轨油腔求解区域的物理模型可简化图1.其长度方向L=50 mm,宽度方向B=30 mm,封油边的宽度b=5 mm.中间区域为进油口,其压力为10 mPa.

图 3 静压导轨油腔求解区域的物理模型
求解区域是一个环形区域的油膜,求解前先定义边界条件.根据压力边界条件可以得出:1)在腔内p=10 mPa,即内部矩形内的p为常数10;2)在四周边缘上p=0 mPa,即在外部矩形的边界上的p为常数0 .将式(2)进行五点差分可以表达如下:

2.2 基于matlab计算方程数值解
按照上述方法先将求解区域划分成如图4所示的网格,划分后的求解区域一共有560个网格节点.根据差分数值解法,即式(3)代替式(2),将问题转化为未知函数p(x,y)在节点(i,j)上的数值位置量的线性方程组Ax=b;A是系数矩阵,是网格节点p(x,y)差分成的560×560的稀疏矩阵(图5).
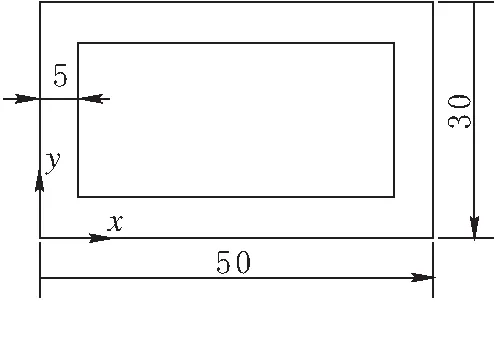
图 4 静压导轨油腔求解区域网格化,mm
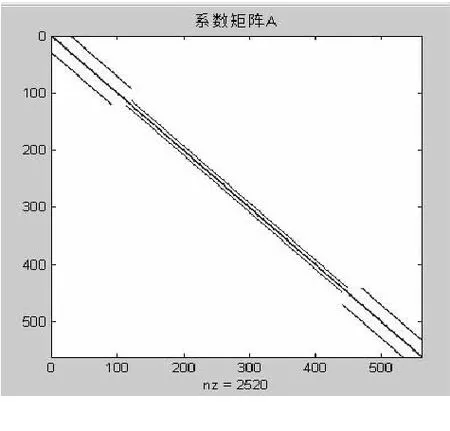
图 5 系数矩阵A
b是560×1的稀疏向量,是进口压力边界条件,表示了进口压力的位置和压力值大小.然后对方程组Ax=b进行Gauss-Seidel迭代法求解,得出的解向量x是压力p的稀疏向量,用matlab中的full函数将其转化成满矩要求的压力分布(图6).
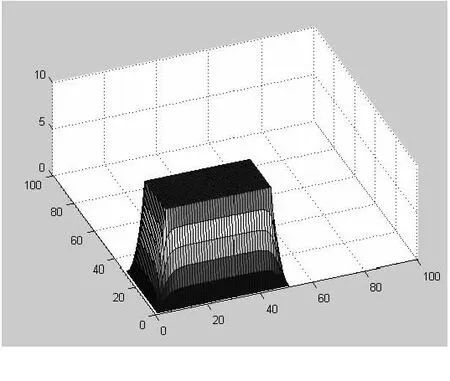
图 6 满矩要求的压力分布,mm
分别做出在中间平面x方向和y方向截面的压力分布曲线(图7).

(a)x方向
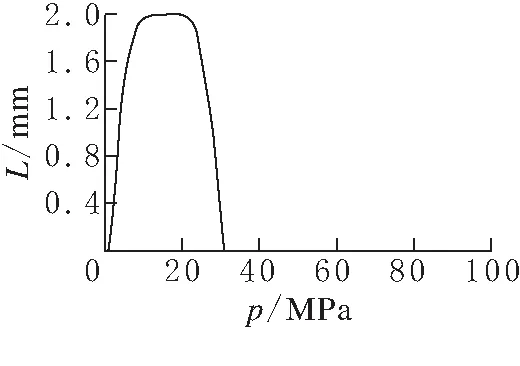
(b) y方向图 7 中间平面截面的压力分布曲线
由图7可以看出:在油腔内部附近区域内,压力分布基本维持在10 mPa左右,从封油边至出口,压力由2 mPa逐渐降到0,存在较大的压降,并且下降呈现明显的非线性.
3 液体静压导轨油膜静态特性参数的计算分析
3.1 液体静压导轨承载能力的计算
在供油方式为定量的情况下,对导轨承载底部区域的压力进行积分,得到导轨的承载能力(图8).
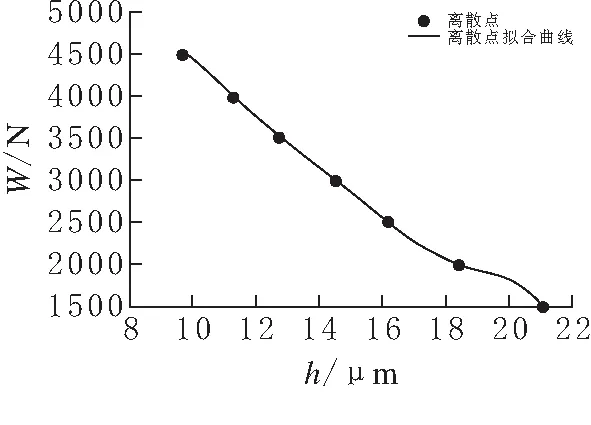
图 8 不同油膜厚度下矩形导轨的承载能力
为进一步研究静压导轨的承载能力特性,将不同油膜厚度下的承载能力用多项式拟合表示.当油膜厚度为10~25 μm时,该导轨的承载能力的数学拟合可近似表示为
W=-124.9h6+20.21h5+335.7h4+
50.57h3-53.97h2-1183h+2895.
式中:W为导轨承载力,N;h为油膜厚度,μm.
3.2 液体静压导轨油膜静刚度的计算
根据导轨在不同油膜厚度时承载能力的计算结果,用式(2)可求出导轨油膜的静刚度,结果如图9所示.当油膜厚度为10~25 μm时,导轨的刚度数学拟合式可以近似表示为
K=-30.06h6-83.23h5+318.9h4+
289h3-834.2h2-276.5h+771.2.
式中:K为导轨油膜刚度;h为油膜厚度.

图 9 导轨油膜的静刚度
4 结论
通过求解雷诺方程计算油膜压力分布,根据导轨静态参数的计算可以得出:静压导轨的承载能力随着油膜厚度的增大呈减小的趋势,静刚度随着油膜厚度的增大,在10~15 μm时呈增长趋势,在15 μm时达到最大值.在15~25 μm时呈减少趋势.
[参考文献]
[1] 赵建华,高殿荣,张作超.液体静压导轨定压供油式油腔承载力的超静定力学模型[J].机械工程学报,2012(22):168-176.
[2] 张逸舟,黄筱调,于春建. 大重型机床静压导轨的静态性能及油膜流体仿真研究[J].机械设计与制造,2012(10):102-104.
[3] 吕 琳,李艳霞.精冲机静压导轨的油膜刚度设计及控制[J].精密成型工程,2010(05):48-51.
[4] 温诗铸. 摩擦学原理[M].北京:清华大学出版社,2011.
[5] Serrato R,Maru M M, Padovese L R.Effect of lubricant viscosity grade on mechanical vibration of roller bearings[J].Tribology International, 2007, 40(08):1 270-1 275.
[6] 梅 怡.新型液体静压支承技术在机床导轨上的应用[J]. 液压与气动,2012(06):83-86.
