复杂环境下多雷达点迹融合*
2013-11-09陈霞
陈 霞
(海军装备部电子部,北京 100841)
与传统的航迹融合相比,点迹融合能够充分利用系统中所有雷达的原始探测信息,有利于扩大有效跟踪范围,缩短系统反应时间,提高跟踪精度,具有抗干扰、抗隐身、抗低空入侵等特点,是多平台协同作战的核心技术。目前研究点迹融合算法主要集中于如何有效利用多雷达点迹数据进行正确数据关联和滤波,而存在杂波干扰、系统误差等复杂环境下的点迹融合问题则很少涉及。但在实际应用中,这些问题却无法避免,若没有相应的解决方案,将导致融合系统出现虚假航迹、冗余航迹、错误跟踪、融合精度降低等问题。因此,本文首先提出了一种复杂环境下的多雷达点迹融合结构框架,并给出了关键技术的模型及算法。
1 点迹融合结构框架
集中式多雷达点迹融合系统是将所有雷达的量测数据发送至融合中心,在融合中心进行数据对准、航迹起始、数据互联、航迹滤波等处理[1],见图1。

图1 多雷达点迹融合结构框架
图1 所示的是一种较为通用的集中式多雷达点迹融合结构框架,但针对复杂的战场环境,要想建立一套完整的、实用的多雷达点迹融合系统,还需要解决更多更为困难的问题,这其中最为重要有以下几个方面。
1)当雷达有系统误差存在时如何进行数据互联
众所周知,雷达系统误差是客观存在,区别仅仅是误差大小而已。对一个完善的点迹融合系统来说,系统误差配准是重要的且必须的环节。但系统误差准确估计的前提是数据的正确互联,而系统误差的存在又给数据正确互联带来困难。因此须重点解决好雷达系统误差配准与数据互联的关系。
2)如何抑制虚假航迹的产生
复杂战场环境中雷达的量测数据中常混杂大量的杂波和干扰,点迹融合系统在进行航迹处理时,易产生虚假航迹,严重时会造成态势模糊,严重影响指挥员实施正确的作战决策,因此须研究抑制虚假航迹产生的算法,以尽可能减少杂波、干扰对点迹融合系统的影响。
3)如何建立一套完成的系统误差配准体系
目前,系统误差配准算法种类很多,有合作目标配准和非合作目标配准,非合作目标配准又可分为绝对配准和相对配准。由于作战态势的复杂性,仅依靠单一的配准算法肯定不能解决所有的配准问题,因此需要建立一个完整的系统误差配准体系。
本文建立系统误差存在下的航迹起始、虚假航迹抑制和完整误差配准模型,并将之纳入整个多雷达点迹融合处理结构模型中,具体如图2所示。

图2 复杂环境下多雷达点迹融合结构模型
2 系统误差存在条件下的多雷达航迹起始
航迹起始目的是从雷达接收到的包含杂波/干扰和噪声的量测数据中发现目标,并给出这些目标的初始状态估计[2]。而对于多雷达点迹融合系统来说,当系统中包含一定的雷达系统误差时,使用传统的航迹起始方法则易产生冗余航迹或错误航迹[3-4]。为改善系统误差存在条件下多雷达航迹起始正确率,本文提出一种基于相关序列整体分配的多雷达航迹起始方法。具体方法描述如下:
1)提取点迹初始相关序列。采用逻辑法提取各单雷达点迹初始相关序列;
2)点迹序列聚类。对最大允许系统误差条件下间距较近的的单雷达点迹相关序列进行聚类;设Ψs={ψs1,…ψsi,…,ψsn}为以雷达 s为信息源的相关序列集合,s=1,2,…,N。每个相关序列中有m个量测,假设各相关序列中量测已对齐至同一时刻。

若两个相关序列满足:s≠t

其中,

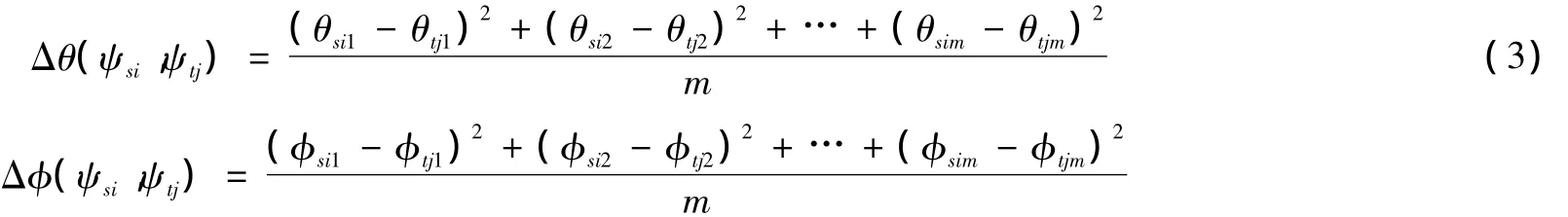
表示两个相关序列之间相似,与具有任一共同相似元的所有相关序列归为一类。
3)相关序列近邻假设整体分配。在距离-方位平面上,按近邻相关的假设进行多维数据整体平移匹配,根据最优匹配结果重构初始相关序列,生成起始航迹,如图3所示。以两个雷达构成的多源跟踪系统为例,设聚类中有N个雷达1构成的相关序列,有M个雷达2构成的相关序列。

图3 分配算法示意图

经相关序列整体分配后,对所有确定为同一目标的非同源相关序列进行“合并”,异类雷达组网时利用三坐标点迹俯仰角的内插外推对二坐标点迹进行补偿,再采用最小二乘算法进行目标初始状态的估计。
3 虚假航迹抑制
假发现率 (False Discovery Rate)是多重假设检验领域一种新的错误测度[5]。其基本思想是在合理的模型假定下计算每个假设的p值,然后按一定准则将该错误控制在某一合理范围内,并尽可能多地发现显著性假设。FDR是指多重假检验中错误的拒绝频数与拒绝频数之比值的期望,即
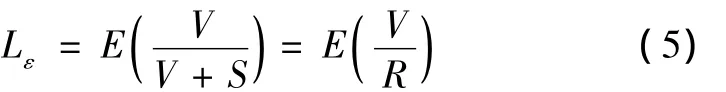
多重假设检验控制的目标是寻找拒绝域,使得总体所犯第一类错误小于设定的检验水平α。假设N个观测值相应的p值为p1,p2,…,pN,对于观测量y的p值定义为

其中,f0(t)是假设H0为真时观测量的概率密度函数。p值可视为一种距离,在一定的模型假设下可以计算p值,当p值较小时,比如小于给定的一个较小的α∈(0,1),说明在原假设下p(y)较小,故可认为距离原假设较远,认为原假设H0不成立,即拒绝H0。
虚假目标辨识问题,可归结为所建立航迹是否源自真实目标的假设检验问题。本文应用FDR方法对虚假目标进行控制,即对需要处理的多个假设检验进行“批处理”而不是传统意义上的逐一进行单个检验,以抑制虚假目标。主要分为以下几个步骤:
1)对每个航迹的假设检验,提出原假设和备选假设为:
H0:该航迹对应真目标;
H1:该航迹对应假目标。
在这样的原假设下,航迹的位置误差应符合雷达的测量误差特性,由此可判断航迹是由对应真目标的测量点建立,还是由杂波或干扰点建立。
2)给出总体的置信水平α,一般取值小于0.05。
3)对每条航迹采用最小二乘方法估计其位置误差,得到检验的统计量(检验残差):

依次计算样本的p值。
4)将计算出的p值按从小到大的顺序排序。
4 误差配准
雷达系统误差配准的任务就是对目标的空间探测信息进行校准,实现多雷达探测同一目标的空间迭合[6]。根据配准依据的基准不同,误差配准算法可分为相对配准和绝对配准;而从是否能够获取到目标的精确定位信息角度出发,绝对配准算法又可以分为基于合作目标的绝对配准和基于非合作目标的绝对配准。
在具体工程实践中,由于战场态势的复杂性及多变性,依靠某单一配准算法根本无法解决所有的配准问题。如相对配准算法主要用于同平台或平台距离相对较近(如图4所示)的雷达误差配准,且配准效果的优劣还依赖于基准雷达的探测精度;而基于非合作目标的绝对配准虽然部分程度上克服了相对配准的缺陷,但该算法对探测平台及目标间的位置关系、参与配准的目标数量及分布等都有很强的依赖性;而基于合作目标的绝对配准虽然理论上能够较好地估计出雷达系统误差且计算简单,但高精度的参考数据常常很难获取。
因此,本文针对工程实际,构建了一个完整的误差配准准则(算法流程如图5所示),具体如下:
1)若已知某雷达没有系统误差,则采用相对配准;
2)若所有雷达均来自同一平台,则采用相对配准;
3)若所有雷达来自不同的平台,则实时计算探测平台与目标的几何位置关系,如果平台距离相对较近,则采用相对配准,否则使用基于非合作目标的绝对配准;
4)若有合作目标存在,则采用基于合作目标的绝对配准算法;当某雷达有估计结果后,则对其他雷达采用相对配准。

图4 探测平台相距相对较近

图5 误差配准算法流程
5 仿真结果分析
5.1 仿真1
本文仿真三批并排飞行的空中目标,三部雷达同时对三批目标进行探测(如图6(a)所示),三部雷达的具体指标如表1。

图6 系统误差存在下的多雷达点迹融合处理效果

表1 三部雷达随机误差与系统误差情况
图6(b)为没有考虑系统误差的多雷达点迹融合处理效果,图6(c)为采用本文提出的考虑系统误差存在下的多雷达点迹融合处理效果。两者比较可以看出:本文所述之方法有效消除了雷达系统误差的影响,没有产生冗余/错误航迹,且航迹稳定连续、融合精度高。
5.2 仿真2
仿真五部分布在不同平台上的雷达,这些雷达分别受到云雨杂波、海杂波以及电磁压制等的干扰(如图7所示);图8为采用本文提出的复杂环境下多雷达点迹融合技术处理后的融合结果。仿真结果表明本文方法能够有效抑制虚假航迹的产生。
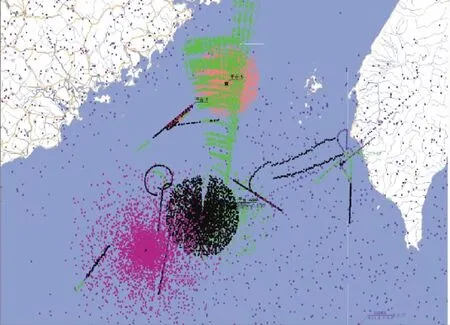
图7 受云雨海杂波、电子干扰影响输出的雷达点迹

图8 多雷达点迹融合结果
6 结束语
本文提出了一种复杂战场环境下的多雷达点迹融合结构框架,并对其中的系统误差存在下的航迹起始、虚假航迹抑制以及雷达系统误差配准等关键技术难题给出了相应的处理模型及算法,仿真结果表明,本文提出的框架、模型和算法,对复杂战场环境有良好的适应性,具有较强的工程应用价值。
[1] 何友,王国宏,关欣,等.信息融合理论及应用[M].北京:电子工业出版社,2010.
[2] 朱洪艳,韩崇昭,韩红,等.航迹起始算法研究[J].航空学报,2004(3).
[3] 于小红,迟建平,周庆军,等.基于点模式匹配的雷达航迹与航行计划匹配算法[J].指挥控制与仿真,2012,34(5):40-45.
[4] 戴霄,潘江怀.基于正则化的多平台导航定位及探测偏差估计方法[J].指挥控制与仿真,2012,34(3):77-81.
[5] Priyadip Ray.A False Discovery Rate Based Detector for Detection of Targets in Clutter Noise[J].IEEE,2008.
[6] 潘江怀.多平台传感器组网的空间绝对配准[D].江苏自动化研究所,2007.
