基于无标度网络的防空反导系统构建

路建伟，姚增建，王 濛

(防空兵学院，河南 郑州 450052)

复杂网络是对复杂系统的抽象和描述，它突出强调系统结构的拓扑特征。复杂网络理论的研究始于20世纪60年代著名数学家Erdös和Rényi提出的随机网络模型。在此后的近40年里，该模型一直是研究复杂网络的基本模型。直到20世纪90年代末，复杂网络的新特征和相应模型相继被揭示，其中包括著名的WS小世界网络模型和无标度网络模型。

现代防空反导系统面临的威胁日益增加，必须集成各种防空反导作战资源，实现防空反导系统内各作战要素之间的信息共享和综合运用，形成一个多武器协同的网络化防空反导体系［1］。而复杂网络理论正是研究复杂网络体系构建的最有效工具，运用该理论的原理和方法，建立网络化防空反导体系使其鲁棒性、抗毁性更好，是赢得防空反导作战的必要条件。

1 复杂网络理论概述

1．1 复杂网络基本模型

网络结构模型是由链路和节点按一定原则构建的组合图。复杂网络可以分为规则网络、随机网络、WS小世界网络、无标度网络、星型网络和集散网络等等。实践证明，现实世界的很多网络都具有小世界特性与无标度特性。

小世界网络(Small-World)模型［2-4］由 D．J．Watts和S．H．Strogat于1998年提出，该模型从规则网络开始，以概率p随机地重新连接网络中的每条边，同时避免自连接和重复边，构造出了一种介于规则网络和随机网络之间的小世界网络。WS小世界网络模型同时具有大的聚集系数和小的特征路径长度的统计特征，即小世界效应，是因为边的重连过程为网络引入了极少量长连接，其他节点间的最短路径通常会优先经过此节点，从而缩短了节点间的距离，使得整个网络的平均距离变小。

无标度网络(Scale-Fee)模型［2-3］由 A．L．Barabasi和R．Albert于1999年提出，其统计特征是网络节点的度服从幂律分布，幂律分布的统计参数与网络大小无关，因此这类网络称为无标度网络。无标度网络具有某些真实网络最常见的两个特性:增长和偏好连接。

1．2 复杂网络的统计特征

用来分析复杂网络的主要统计特征量［2-5］有以五个。

1)边数节点比(L/N):用于比较不同规模网络的边数密度，该参数主要用于衡量构建网络所消耗的资源量，以及衡量网络的复杂程度。

2)平均路径长度(CPL):定义为网络任意两个节点间距离的平均值，即

其中，dij为网络中i和j两个节点之间的最短路径上的边数。CPL值表示网络传递信息的能力。平均路径长度值越大，说明网络中信息的流动、共享与同步越困难，使作战网络为各作战单元提供迅速、准确、有效的共享态势感知越难，进而造成作战单元间协同和同步将难以实现。

3)度分布:一个节点的度定义为此节点连接的边数，可用分布函数P(k)描述具有相同节点度的出现概率，称为度分布。如果网络的度分布为幂率分布，则为无标度网络。无标度网络具有自催化能力:只需改变5% ～10% 的链路连接，就可以重新配置网络效能［6］。网络化防空反导体系应尽可能具有幂率的度分布特征，使作战网络可重新配置。

4)网络聚集系数(C):网络中所有节点聚集系数的平均值。节点i的聚集系数Ci为与该节点连接的ki个节点之间实际存在的边数和总的可能边数的比值。

其中，ki为与节点i连接的邻节点数量;Ei为与节点i相连的ki个节点之间实际存在的边数。

在作战网络中，聚集系数有两个方面的含义:一是表示在完成某个作战任务时，同一作战编组内各单元之间相互协调的能力;二是网络重建中的重要性表示，例如，防空反导网络结构在遭受敌方的打击时失去了与一些作战单元的联系，而聚集系数较高的作战单元可以通过任意节点与网络的重要节点取得联系而有效完成网络重建。网络化防空反导网络应该具有较大网络聚集系数。

通常来讲，一个节点数少于50的网络是不会产生显著的网络化效能［6］，所以假设网络节点为70，采用软件Pajek生成相关网络，WS小世界网络与无标度网络统计参数比较如表1所示。

表1 两种网络参数对比

由表1可知，小世界网络和无标度网络的边数节点比和平均路径长度较小，网络聚类系数较大。无标度网络的平均路径长度更小一些，聚类系数更大一些，更为重要的是无标度网络的度分布服从幂率，当遭到敌方攻击，需要临时改变部队配置时，无标度网络模型只需变更几个度较大的节点则能很轻易地实现网络的自适应重组，避免其遭受毁灭性打击。因此，无标度网络更能满足防空反导网络体系的构建需求。

2 基于无标度网络的防空反导网络模型

2．1 基于无标度网络的防空反导网络模型

文献［4］中给出了传统防空反导网络模型与基于WS小世界网络的防空反导网络模型。设防空反导系统节点与文献［4］一致，无标度网络更能满足防空反导网络的构建需求。则用无标度网络建立防空反导网络模型。

防空反导系统节点假设:1个战役级指挥控制中心，它与下属10个防空导弹战术级指挥控制中心和3个预警雷达战术级指挥控制中心之间连通;每个防空导弹战术级指挥控制中心配置4个防空导弹火力单位，每个预警雷达战术级指挥控制中心配置3个预警雷达单位。指挥控制节点14个，火力节点40个，预警雷达节点9个，共计63个节点。

战术级和火力单元各个节点按照无标度网络模型进行构造［7］，即

1)基本网络结构。初始网络为1个战役级指挥控制节点、1个战术级指挥控制节点、1个防空导弹火力节点、1个预警雷达指挥控制节点和1个预警雷达节点，5个节点上下级相连，且预警雷达指挥控制节点与战术级指挥控制相连。

2)节点数目增长与边的连接过程。增加1个节点，该节点首先连接到上级节点上，然后再随机连接到2个已经存在的节点上，其连接法则为新节点选择某个节点i的概率Pi正比于这个节点i的度数，即

该防空反导系统的无标度网络模型如图1所示。

2．2 防空反导系统网络的统计特征

复杂网络的主要统计特征是网络复杂性分析的重要参数。取复杂网络5个统计特征参数:N为节点数、M为连边数、＜k＞为平均度、C为网络聚集系数、CPL为平均路径长度(CPL)，基于无标度网络模型的防空反导统计特征与文献［4］中网络A、B、C比较如表2。

图1 基于无标度防空反导系统网络模型

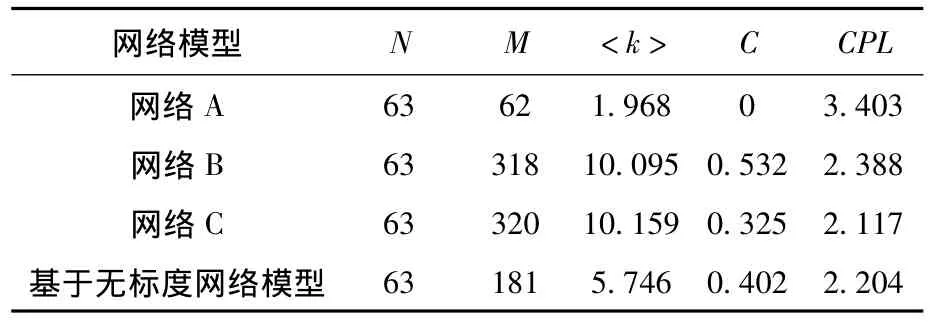
表2 网络模型主要统计特征表

网络A、B、C的统计特征值来源于文献［4］，网络A为传统防空反导系统网络模型，网络B、C为基于WS小世界网络的防空反导系统网络模型，边重连接选择概率 P分别为0．1与0．3。

由表2可知，传统防空系统网络模型连边少，平均度低(仅为1．968)，集聚系数很低(为0)，平均距离却很大(为3．403)，反映出这种网络连边少，节点之间联系少，信息传播距离长，网络效率很低;而基于WS小世界网络的模型网络B、C与基于无标度网络模型都有大的网络聚集系数和小的平均路径长度。网络聚集系数大表示防空反导网络系统的抗毁能力较强，当某些节点被破坏时，能较快地通过其他节点连接重组网络。平均路径长度小表示节点间的联系紧密，信息传播速度快。

当网络中的边与节点总数的比值超过4时，网络即有可能由于存在过多的向前和向后的反馈环路使网络瘫痪［3］。一般情况下边数节点比(L/N)约小于2，过大网络开销太大，过小网络很脆弱［6］。基于无标度网络模型边数仅为181，比网络B、C开销小，但达到了同样的网络效果。

文献［4］中平均度定义实际是边数节点比(L/N)的2倍，意义不在于对网络鲁棒性分析，而在于边数节点比的分析，边数节点比(L/N)越大，网络的开销越大。

基于无标度网络模型的节点度分布统计见表3。

表3 节点度分布统计表

由于无标度网络的度分布服从幂率，即P(k)=ck－r，其中c为常数，k为节点的度，r为度指数。当一个网络的节点度服从度指数介于［2，3］之间的幂律分布时，就说明该网络符合无标度网络［8］。将表3数据导入到MATLAB中，拟合得到c=1．8582，r=2．1593，介于2～3之间，基于无标度网络模型所生成的网络节点的度分布符合幂律分布，因而所得网络符合无标度网络特征。将其度分布用双对数曲线作图如图2所示。

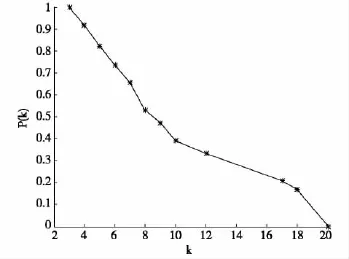
图2 网络节点度分布图

图2 与文献［4］中相比较，基于无标度网络模型比网络B、C网络中心化程度更低，网络的鲁棒性更好，即网络重组性更强，网络抗毁能力更出色。

3 结束语

本文提出了基于无标度网络的防空反导系统网络模型，并将其统计特征同基于WS小世界网络的模型进行了比较，得出基于无标度网络度分布为幂率分布，更适合防空反导系统网络模型的构建。所构建的防空反导系统网络模型有更好的网络平均度，节点间联系紧密，信息传播速度快，网络的鲁棒性更好，对一体化防空反导系统的构建具有一定参考意义。

［1］ 张强，雷虎民．复杂网络的防空反导网络特征［J］．火力与指挥控制，2011(10):41-44．

［2］ 杜巍，蔡萌，杜海峰．网络结构鲁棒性指标及应用研究［J］．西安交通大学学报，2011(4):93-97．

［3］ 龙真真，张策，王维平．基于复杂网络的作战网络分析［J］．火力与指挥控制，2010(8):8-12．

［4］ 张强，雷虎民．基于小世界网络的防空反导系统复杂性研究［J］．现代防御技术，2010(6):1-5．

［5］ 王波等．WS与NW两种小世界网络模型的建模及仿真研究［J］．浙江工业大学学报，2009(2):179-182．

［6］ 杰夫·凯尔斯，于全译．分布式网络化作战［M］．北京:电子工业出版社，2006:83-87．

［7］ 王忻．多传感器信息融合系统改进型BA模型［J］．航天控制，2008，(1):51-55．

［8］ 汪小帆，李翔，陈关荣．复杂网络理论及其应用［M］．北京:清华大学出版社，2006:33．