摆线桨气动性能研究进展
2013-11-09唐继伟宋笔锋
唐继伟,胡 峪,宋笔锋
(西北工业大学 航空学院,陕西 西安 710072)
0 引 言
摆线桨是一种桨叶展向同旋转轴轴向平行的推力装置[1](图1a),通常由两个以上桨叶组成,桨叶在绕摆线桨转轴公转的同时还绕铰链作俯仰振荡运动。悬停状态时,桨叶的运动轨迹为圆周,而在前飞状态下桨叶运动轨迹为摆线(图1b),故名摆线桨[2]。
与旋翼和螺旋桨相同,摆线桨也是一种通过数个桨叶绕转轴旋转产生推力的旋转翼推力装置。不同之处在于:由于摆线桨桨叶在旋转时展向与桨轴平行,桨叶展向的每个叶素都工作在相似的气动条件下(如相似的流速、雷诺数和迎角),因此桨叶气动力分布相对均匀,理论上桨叶能够被优化到最佳气动效率;由于桨叶周期性俯仰振荡,桨叶产生的是非定常气动力,桨叶动态失速过程可产生高升力;另外,由于摆线桨推力方向几乎能在垂直于桨轴的任意方向进行瞬时调节,其相比传统螺旋桨和旋翼系统,在提高飞行器(特别是微型飞行器)的机动性能方面具有很大优势[1]。因此,将其作为未来垂直起降飞行器、高空长航时无人机、飞艇和舰船等诸多领域的推进系统[3]具有很好的应用前景。
摆线桨研究可以追溯到20世纪20年代[4],美国海军与华盛顿大学研究了摆线桨应用在飞艇上的可能性,但最终失败。Wheatley等人[5-6]完成了早期摆线桨气动力试验,由于缺少对摆线桨设计参数的系统性研究,他们完成的这些实验并没有能够证明其具备比旋翼、螺旋桨等升力和推进装置更优越的气动性能。二战以后,随着旋翼等装置的广泛应用,摆线桨研究一度中止。
20世纪90年代末,随着材料和控制等相关学科发展,摆线桨重新引起了国外研究者的极大关注,美国海军、Bosch Aerospace公司与密西西比州立大学[7-9]、马里兰大学[1,10-20]、韩国首尔大学[21-24]、日本筑波大学[25-27]和以色列宇航工程技术研 究中心(TITT)[28-29]等机构已在摆线桨研 究领域取得了一系列成果。在国内,西北工业大学近年开展了摆线桨相关研究工作[30-34],研制了摆线桨飞行器原理样机并成功实现了可控飞行[35]。
气动性能是影响摆线桨应用前景的关键因素,对于摆线桨气动性能及非定常流动机理的研究具有十分重要的理论意义和工程应用价值。目前,国外研究虽然已经取得了一些成果,但仍处于发展中,相关文献并不多,还有许多关键问题亟待解决;而国内相关研究极少,有必要对其进展和现状给予关注,综合评估其应用潜力和发展方向。
本文介绍了摆线桨气动力产生的基本原理和主要特点,从理论研究、数值模拟和实验研究三个方面综述了摆线桨气动性能研究进展,对摆线桨气动效率进行了探讨,并对未来摆线桨气动性能研究方向作出了展望。
1 推力产生原理及气动力主要特点
1.1 推力产生及矢量推力原理
图1为一个4桨叶摆线桨示意图,图1(a)为构成三维图,其主要由桨叶(Blade),转轴(Rotating shaft),支架(Support arm),推拉杆(Push rod)和偏心圆环(Eccentric ring)构成,图1(b)为其中一个桨叶在摆线桨水平前飞状态下时的运动轨迹。

图1 摆线桨示意图Fig.1 The three-dimensional sketch map of cycloidal propeller and the orbit of a blade in forward flight
摆线桨产生气动力的基本原理如图2所示,图中V为桨叶做圆周运动的切向速度,α为桨叶瞬时迎角。当偏心圆环(Eccentric ring)圆心(Offset point)相对摆线桨转轴轴线(Axi centre)有一偏心距时,桨叶旋转到上半周和下半周都是正迎角。转动一周过程中,所有桨叶产生的瞬时升力、阻力投影到竖直方向和水平方向的力的平均值即为摆线桨的竖直推力和水平推力。通过控制机构改变偏心圆环的偏心距,可以改变桨叶的俯仰振幅,从而改变摆线桨的推力大小。
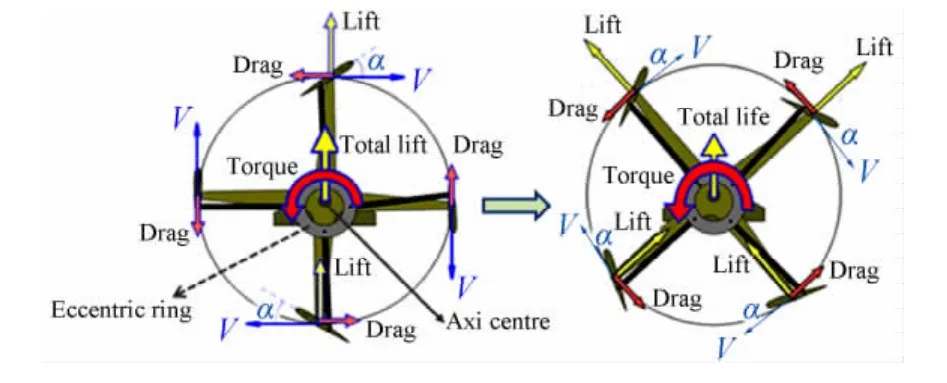
图2 产生推力的基本原理Fig.2 The production principle of thrust
当摆线桨转动过程中需要调节推力方向时,可通过控制机构拉动偏心圆环,改变其偏心角度(ε),从而改变桨叶瞬时迎角随方位角的变化规律,产生垂直于转轴的平面内360°任意方向上的推力,实现不同飞行状态下推力方向的瞬时改变。图3给出了改变摆线桨推力方向的原理示意图。当偏心圆环圆心分别处于摆线桨轴线正下方(ε=90°)、左下方(ε=45°)、左侧(ε=0°)和左上侧(ε=-45°)时,其推力分别指向正上方,右上方,正右方和右下方。

图3 产生矢量推力原理Fig.3 The production principle of vector thrust
1.2 气动力主要特点
1.2.1 桨叶俯仰振荡产生非定常升力
摆线桨桨叶运动规律为绕圆周的周期性俯仰振荡,桨叶剖面迎角按照近似正弦规律变化,这导致了很强的非定常流动状态,可能出现动态失速现象,带来如图4所示的非定常动态升力,图中CN为翼型俯仰振荡时的法向力系数。因此,即使处于悬停状态下的摆线桨,桨叶上的气动力变化也是一个很复杂的动态过程,这使得定常和准定常的翼型气动力理论模型已经不适合于摆线桨气动力分析,需要采用合适的非定常流理论进行研究。
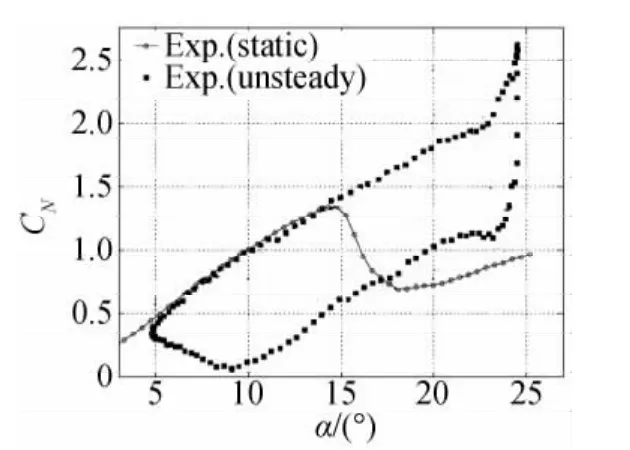
图4 翼型非定常升力与静态升力实验值的比较[36](马赫数Ma:0.12,减缩频率k:0.124,翼型NACA 0012)Fig.4 Comparison with experimental unsteady lift and steady lift(Ma=0.12,k=0.124,NACA 0012)
1.2.2 桨叶之间非定常干扰严重
摆线桨通常由2~6个桨叶组成,因此,桨叶非定常运动产生的尾流会对其他桨叶气动性能产生很大的影响。这与螺旋桨桨叶干扰不同:无来流情况下,定距螺旋桨桨叶绕桨毂转动时桨叶之间无相对运动,因而干扰几乎是恒定的;而摆线桨每个桨叶都在作周期性振荡运动,使得桨叶之间的干扰成为更加复杂的非定常干扰问题。
2 理论方法研究
理论方法具有快速高效的特点,在工程应用上具有重要意义。建立合理的摆线桨气动力理论模型的关键在于如何更好地分析桨叶非定常气动力和桨叶干扰等气动力特点。目前,这方面的文献还很少,下面按照求解桨叶非定常升力时是否考虑了流体粘性分别介绍:
2.1 基于无粘流假设的气动力模型
Mcnabb[9]提出了基于薄翼振荡理论[38]的摆线桨气动力计算模型。该模型基于叶素理论计算桨叶的升力特性,假设流动为无粘流,采用翼型在定常流动条件下对应迎角时的零升阻力系数估算桨叶零升阻力,引入由实验结果修正得到的经验参数估算桨叶诱导阻力,并据此得到摆线桨的功耗(扭矩乘以转速)。模型中采用入流效应分析各处下洗速度,基于均匀入流假设的单流管模型如图5所示。图中,Vt为入流速度,T为摆线桨拉力,D为摆线桨直径。
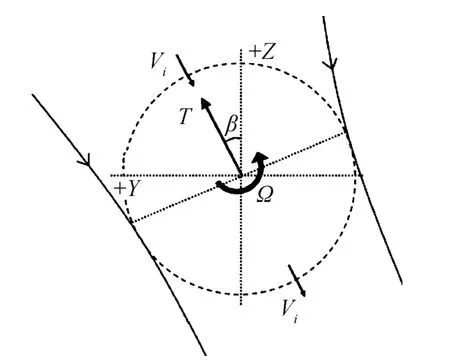
图5 单流管模型示意图[10]Fig.5 A diagrammatic sketch of single stream-tube
假设整个摆线桨完全浸处于一个流管中,入流速度Vi的大小在流管各处假设为恒定,其估算公式为:
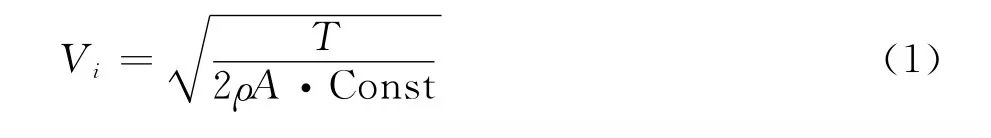
式中,T为摆线桨推力,ρ为空气密度,A为桨盘矩形投影面积(大小为摆线桨直径乘以桨叶展长),Const为经实验数据得到的桨盘面积修正系数。Vi的方向在迭代过程的每一周期中随着合力方向而改变,桨叶运动到各处的来流速度为转动引起的沿圆周切向速度叠加上Vi之矢量和。该模型计算结果与实验值吻合较好,但文中的经验参数是由他们的实验数据修正得到的,这限制了其适用性。
Benedict[10]对基于流管模型的摆线桨气动力分析方法进行了发展。该模型同样假设流动无黏,基于薄翼理论得到翼型非定常升力和力矩的解析解。采用基于非均匀入流假设的多-双流管模型,与采用单流管模型时的计算结果进行了对比,结果表明采用两种流管模型得到的合力计算值均与实验数据吻合较好,采用多-双流管模型精度更高,而两者对合力方向的计算精度均不够高。该方法相对Maccnb模型的发展主要在于:计算过程未引入桨盘面积修正系数等经验常数,更具一般性;多双流管模型相比单流管模型更为细致地考虑了各处下洗速度,更加符合实际流场中的速度分布,因而可以提高计算精度。
胡峪[37]将非定常涡格法(UVLM)应用到求解摆线桨气动力的计算中。非定常涡格法[38]的基本原理是假设流动无粘无旋,将桨叶表面划分成多边形网格,在各网格上布置涡环。求解时采用时间推进法,在第一个时间步,没有尾涡存在,而仅有桨叶上的涡环。经历一个时间步后,涡环从桨叶后缘不断脱落,并以当地速度随流体一起向下游运动。在运动过程中,各涡环强度需保持不变,以满足理想流中的Kelvin环量守恒定理,并认为这样就近似满足了库塔条件,且尾涡不受力。通过物面边界条件,求解每一个时刻关于各涡环环量的线性方程组,再通过伯努利方程即可得到桨叶上的压力分布和气动载荷。图6(a)是应用该方法得到的气动力曲线,可以发现其虽具有一定精度,但与实验数据仍有较大误差;图6(b)是桨叶尾迹的计算结果,可以看出,其并未得到桨叶尾迹由于下洗流影响向摆线桨下游流动的现象,这与实际观察得到的情况不符[1]。
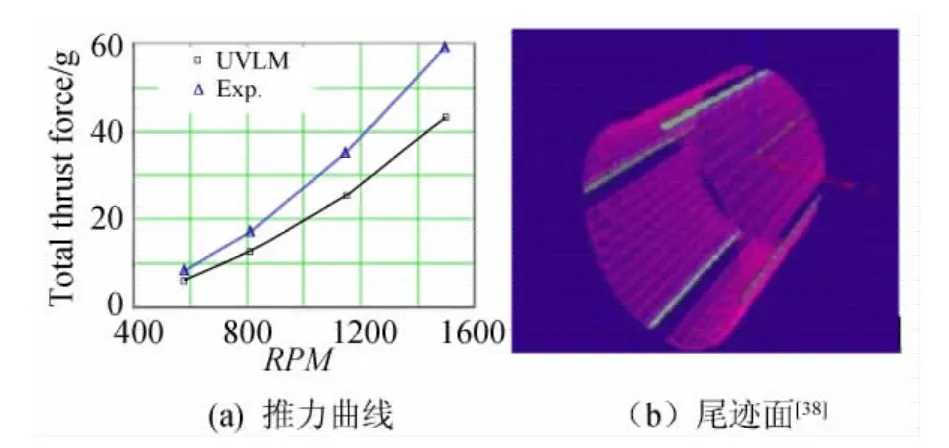
图6 应用UVLM方法[38]求解的摆线桨推力和桨叶尾迹Fig.6 The thrust and wake structure of cycloidal propeller[38]
采用非定常涡格法对摆线桨气动性能进行分析的优点是:考虑了桨叶间的气动干扰;能对复杂桨叶外形进行分析,且计算量适中,具有一定精度。
以上三种摆线桨非定常气动力理论模型的共同的局限是:都未考虑流体粘性,不能考虑具有分离流动和前缘分离涡的情况,因此只适用于减缩频率低、桨叶迎角振荡幅度小和未发生动态失速的流动情况,计算时经常出现较大误差。
2.2 考虑流体粘性的气动力模型
唐继伟和胡峪[30-31]提出采用 Leishman-Beddoes(LB)动态失速模型的状态空间法[39-40]来对摆线桨气动性能进行分析。
该方法中采用的LB模型是研究翼型非定常气动力的一种半理论半经验模型[39],给出了翼型出现前缘分离涡的判断准则及其位置和离体涡长度如何确定的方法,可以很好的计算翼型俯仰振荡非定常升力,在直升机旋翼和风力机设计中应用广泛。LB状态空间模型[40]在每一时刻需要求解含12个状态量的一阶微分方程组,包括8个从指数响应推导而来的线性附着流动状态量,3个描述后缘分离产生的非线性气动响应的状态量,和一个用来判断动态失速及流动重新附着的状量。
采用该方法得到的计算结果与实验数据吻合较好[30-31]。与 Maccnb和Benedict理论模型相比,采用LB模型的气动力模型的改进主要是考虑了流体粘性,因而可以考虑具有后缘分离、前缘分离涡和动态失速的影响[30]。但由于采用单流管模型估算各处入流速度,因而不能对桨叶间的尾流干扰作细致分析;而基于叶素理论,不能很好地估算桨叶诱导阻力。
总的来说,目前尚还没有一个精度高、应用广泛的成熟摆线桨气动力理论计算模型,需要发展无需引入经验参数,并能计入考虑了流动粘性的桨叶非定常气动力特性和桨叶干扰的理论计算方法。
3 数值模拟研究
计算流体力学的发展为摆线桨的非定常流场提供了一种有效的分析手段。近年来,国外研究者对摆线桨悬停状态下的流场和气动性能展开了为数不多的数值模拟研究:
首尔大学的Hwang等人应用Star-CD软件的非定常计算模块对摆线桨进行了数值模拟[22-24],得到了其在悬停状态下的流场和气动力的周期性特征[24],并利用数值模拟对摆线桨的气动力进行计算,设计了一个安装四个摆线桨的飞行器,实现了系留悬停[23]。为了模拟桨叶运动,采用滑移网格技术,将摆线桨全域(外圆域)作为转动域,而每个桨叶周围的小圆形子域作俯仰振荡运动。他们对得到的数值模拟结果分析发现:下洗流穿过摆线桨内部时没有弯曲;即使偏心方位角为零,摆线桨下游的出流偏离竖直方向也有10°~20°,如图7所示,这与PIV实验观察到的定性一致;桨叶振荡幅度一定时,其在圆周底部(ψ=270°)时的合力比在顶部(ψ=90°)时大,如图8所示,他们认为这是弦线“弯度效应”造成的。
以色列的Gill Iosilevskii等人采用他们自己发展的计算程序EZNSS对摆线桨气动性能进行了数值模拟[28-29]。该程序将流动假设为层流,采用非定常完全可压缩N-S方程作为控制方程,采用非定常隐式时间推进。网格系统采用的是结构化嵌套网格,包括两部分,随摆线桨桨叶运动的CH型桨叶网格和笛卡尔背景网格。研究的摆线桨弦长1.5cm,展长15cm,桨盘直径7.5cm,桨叶振幅15°~25°,转速10000RPM,对应雷诺数为40000。通过对流线图分析,他们发现摆线桨流场中两侧出现了较大的成对卷曲涡(Distorted Doublet),如图9所示,这与有来流情况下的圆柱绕流产生的Magnus效应[41]类似。
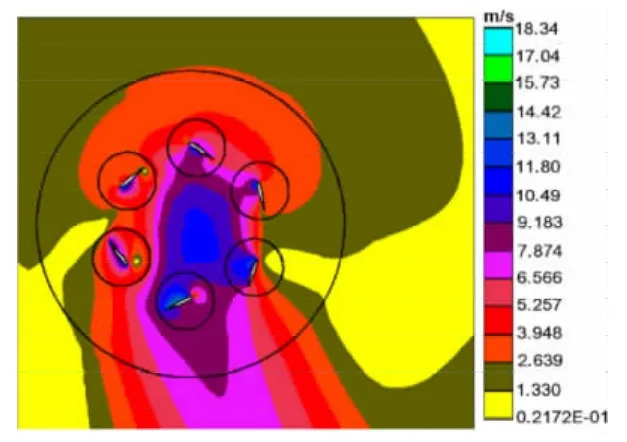
图7 速度云图Fig.7 The velocity magnitude contour
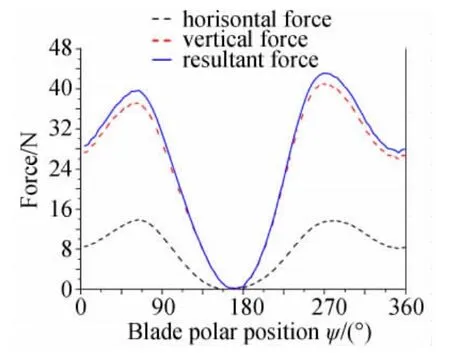
图8 桨叶转动一周的法向力、侧向力与合力[24]Fig.8 Horizontal,vertical and resultant forces produced by a blade during one cycle of rotation[24](CFD analysis)

图9 瞬时流线图[28-29],10000RPM,Re=40000Fig.9 Instantaneous streamlines[28-29],10000RPM,Re=40000
美国马里兰大学的Yang[20]通过基于结构化嵌套网格求解了预处理后的可压缩非定常雷诺平均(RANS)方程,空间离散采用中心格式有限体积法,非定常隐式时间推进采用双时间法。采用嵌套网格技术,将C-O型桨叶网格嵌套于圆柱形背景网格。在生成网格时,采用Benedict等人对摆线桨的结构动力学分析方法[18]考虑了桨叶展向的弯扭变形。对2桨叶摆线桨的气动性能和流动特征进行了二维和三维数值模拟,得到的竖直方向的力与实验数据吻合较好,但水平力和功耗与实验值有较大误差。
综合来看,国外虽已经开始了一些摆线桨的数值模拟研究,但由于摆线桨绕流是极为复杂的低雷诺数强非定常流场,对于出现的漩涡等结构现有文献中数值模拟的精度均不是很高;很少利用数值模拟方法对摆线桨力学特性进行深入分析,而国内对于摆线桨的数值模拟研究则刚刚起步,还需要大量的研究工作。
4 实验研究
摆线桨设计参数主要包括:桨叶数、桨叶弦长、展弦比、桨叶实度、翼型、俯仰轴在弦向的位置和桨叶在上下半周的振荡幅度等。由于摆线桨运行时桨叶所受到的离心力和振荡带来的惯性力较大,对单个桨叶的气动力进行测量难度很大,因此,目前实验中仅限于测量摆线桨总的推力和气动功耗,且多为静拉力实验。通常采用动量理论分析摆线桨的悬停气动性能,将其悬停效率FOM(figure of merit)定义为[1]:

其中,功率载荷PL为单位功耗产生的推力,即:

桨盘载荷DL为单位桨盘面积产生的推力,即:

气动功耗:

以上各式中,T、A与公式(1)中定义相同,Ω为摆线桨气动扭矩,ω为摆线桨转动角速度。相同桨盘面积下,桨盘载荷相等时FOM大(即功率载荷大)的悬停效率高。摆线桨的前飞气动效率定义与螺旋桨相同,定义为:

式中,Vtowards为摆线桨前飞速度。
美国海军资助Bosch Aerospace公司与密西西比州立大学合作,研究摆线桨在飞艇上的应用前景[9]。他们设计了一个桨径为1.22m、展长1.22m、弦长0.305m,NACA0012翼型的6叶摆线桨,并进行了一系列的静拉力测试,以功率载荷(单位功率产生的拉力)为衡量指标,得到的结论是摆线桨的气动性能比螺旋桨和涵道风扇好很多。但他们并没有说明该比较是否在相同桨盘载荷下进行的。
首尔大学对摆线桨的桨径、桨叶俯仰振荡幅值、偏心方位角等参数进行了研究[24],图10是他们的实验装置。摆线桨展长0.8~1.0m,弦长0.15m,NACA0012翼型,转速0~600RPM,桨叶振幅5°~30°,测试的桨叶数分别为2叶、3叶和6叶桨。他们发现:桨径变大,桨盘面积增加,其气动效率也越高,这与旋翼和螺旋桨相同;而桨叶振幅在一定范围内变大时其气动效率也在增加。在对桨叶数的影响进行实验时发现,在相同桨盘载荷下,3叶桨比2叶桨的功率载荷高,而6叶桨最低。他们将1m桨径摆线桨产生某一拉力时的功率载荷与旋翼的功率载荷相比,发现摆线桨的功率载荷更高。但同样未指明是否在相同桨盘载荷作的比较。

图10 首尔大学测力实验装置[24]Fig.10 Experimental setup in Seoul National University
日本筑波大学对三个桨叶的摆线桨[25-26]进行了实验。摆线桨桨径2m,展长1m,弦长0.3m,NACA0012翼型,测试转速60~600RPM。他们发现摆线桨合力方向与竖直方向有约10°的偏角,这与Hwang[24]等人的数值模拟结果是定性一致的,且只有在桨叶迎角不断改变过程中能观察到,而在迎角不变(定距)的情况下无此现象[26]。
胡峪[2]在新加坡国立大学对小型摆线桨进行了实验与分析。实验中采用的摆线桨为3叶桨,桨径140mm~270mm,展长140,梢跟比0.2~1.0,NACA0012和平板翼型,桨叶上半周(U)和下半周(D)振幅组合为 U45°D10°、U40°D35°、U20°D40°、U17.5°D45°、U5°D50°。他对实验结果进行分析,发现在低雷诺数(1000~10000)下:薄翼型、矩形桨叶(展弦比为1)和上半周振荡幅值小而下半周振荡幅值大的设计可以使得摆线桨的效率较高。
以色列宇航工程技术中心[28-29]开展了摆线桨的相关气动力实验工作。摆线桨展长0.11m,弦长0.022m,直径0.1116mm,属于微小型摆线桨,如图11所示,采用NACA0015翼型,振幅为0°~40°,转速为4000RPM到6000RPM(相应的雷诺数为36000~50000)。实验结果表明,安装两个桨叶的摆线桨在桨叶俯仰运动振幅为26°时开始失速;而4桨叶摆线桨在桨叶俯仰运动振幅为32°时开始失速。另外,摆线桨拉力偏转方向可达10°~40°,且偏转角随着拉力增大而呈减小趋势。

图11 微小型摆线桨[29]Fig.11 Experimental micro-scale cycloidal propeller[29]
最近几年,马里兰大学摆线桨研究团队完成了大量摆线桨气动力实验,取得了一些重要成果[1,10-20]。实验中采用的摆线桨桨径和桨叶展长都约为0.15m左右,属于微小型摆线桨,如图12所示。他们对桨叶数、桨叶俯仰振幅、翼型、弦长、桨叶俯仰轴位置等对气动性能的影响进行了研究。发现在相同桨盘载荷下:桨叶俯仰轴在弦向距前缘35%~45%弦长位置处效率最高;相同桨叶实度时,桨叶数越少效率越高;且桨叶振荡幅度适当增大对提高摆线桨的气动性能有利;而桨叶沿展向弯曲、扭转变形和翼型弯度会对气动性能带来不利影响。另外,实验中发现采用厚翼型和上半周振幅大、下半周振幅小时有利于提高气动效率,这与胡峪[2]的实验结论相反。

图12 马里兰大学微小型摆线桨实验[19-20]Fig.12 The experimental of micro-scale cycloidal propeller model in the University of Maryland[19-20]
马里兰大学摆线桨研究团队的另外一个重要贡献是:完成了摆线桨悬停状态下的粒子成像(PIV)实验[1,20],揭示了一些重要的摆线桨流动现象和流场特征,主要为:观察到桨叶会受到很强的下洗速度,图13(a)所示得到的是不同尾迹寿命角(Wake age)时尾迹沿桨叶展向的无量纲速度分布,可以看到,尾迹平均速度可达60%~70%桨叶转动速度[1],使得桨叶的有效迎角大大减小,这解释了为何桨叶振幅较大却并未失速;图13(b)是测得的桨叶附近涡量云图,可以看到,桨叶上表面出现了前缘涡,这会带来前缘吸力;另外,他们也观察到了穿过摆线桨的尾流出现弯曲,解释了摆线桨出现侧向力的原因,指出这是摆线桨转动带来的 Magnus[41]效应;PIV实验对于分析摆线桨的流动机理和验证数值模拟的有效性具有重要意义。
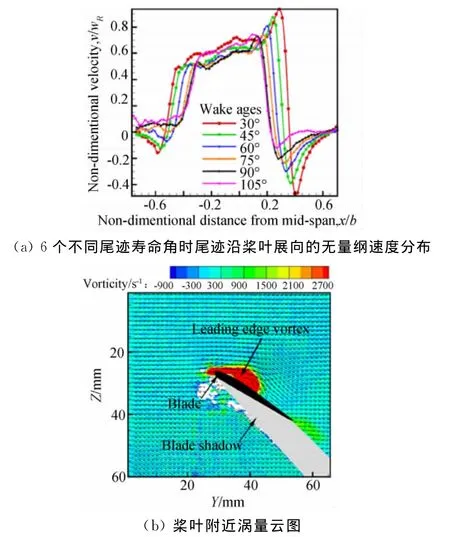
图13 PIV实验结果[1]Fig.13 The results of PIV experiment[1]
由于对摆线桨的关键设计参数对气动性能的影响还不够了解,马里兰大学早期微小型摆线桨静拉力实验得到的气动性能数据并没有微型旋翼等升力装置好[10-14]。在最近的实验[19]中,经过对设计参数 进行较为详细的系统化实验,找到了一个目前为止的最优微型摆线桨设计方案:4叶桨、NACA0015翼型、桨叶在上半周的最大振幅为45°、在下半周的最大振幅为25°,桨叶俯仰轴位于25%弦长处。采用对参数优化设计后的摆线桨模型进行静拉力实验,与相近桨盘面积的微型旋翼对比发现(图14),在相同桨盘载荷时摆线桨的功率载荷比微型旋翼[17]高出很多。
5 摆线桨气动效率探讨
目前文献中关于摆线桨与旋翼、螺旋桨等升力装置或推进器相比,气动效率高低的结论并不完全一致:某些文献中,如文献[7]认为摆线桨的气动效率高,但他们所作的功率载荷对比图并没有说明是否在相同桨盘载荷下进行比较,因此结论不具有足够的说服力;而某些实验是在对摆线桨的设计参数对气动性能影响不了解的情况下完成的,因此得到了摆线桨气动性能不如旋翼等装置的结论,这从马里兰大学近年来的微型摆线桨实验研究历程中可以看到[10-14]:随着摆线桨研究的不断深入,在对设计参数进行细致优化后,得到的相同桨盘载荷时微型摆线桨的功率载荷实验数据要比微型旋翼高出很多[19]。由此可以看出,不同的摆线桨设计方案会大大影响摆线桨的气动性能和效率高低,这也可能是不同研究者得到的实验结论不一致的原因。然而,同螺旋桨、旋翼等技术的发展历程一样,这也是摆线桨研究必然经历的过程。
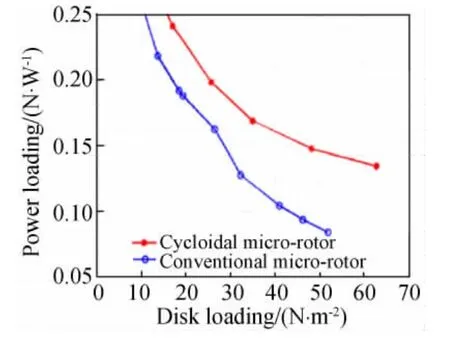
图14 优化后的微型摆线桨与旋翼功率载荷对比图[25]Fig.14 Power loading comparison between optimized micro-cycloidal propeller and micro-rotor[25]
综合来看,从现有实验数据分析,相同桨盘面积相同桨盘载荷时,摆线桨能够具备比旋翼、螺旋桨等升力和推进装置更高的功率载荷[19],而若对摆线桨重要设计参数进行进一步优化,则其气动效率还有可能进一步提高。
6 总结与展望
摆线桨是一种新型全向矢量推力装置,近年来已成为国外航空领域研究热点,引起了极大关注,国内外已研制出采用摆线桨作为升力、推力源的三轴(双摆线桨垂直机身同轴转动、一轴螺旋桨锁尾)和四轴(四个摆线桨垂直机身呈双排串列)等布局的垂直起降飞行器原理样机,并初步实现了可控飞行,同时展开了将摆线桨作为飞艇等飞行器推进装置的应用研究。总的来看,对摆线桨非定常空气动力学特性的分析、流动机理的研究以及如何提高摆线桨气动效率仍是目前摆线桨研究的技术难点。本文综述了国内外摆线桨气动性能研究进展,总结并展望如下:
(1)现有文献中对摆线桨气动效率高低的结论并非一致,但多认为摆线桨效率更高,且从最近马里兰大学的静拉力实验数据[19]来看,至少摆线桨悬停状态下的气动性能可优于旋翼等升力装置,具备很高的工程应用潜力,值得国内研究人员关注。
(2)由于摆线桨的强非定常气动特性,摆线桨空气动力学理论仍不完善,目前的理论模型多存在着精度不够高、适用性窄等不足。需要发展能够考虑桨叶动态失速、桨叶诱导阻力和下洗干扰等因素的理论模型。
(3)摆线桨流动机理研究仍是难点,理论上,摆线桨可以利用俯仰振荡带来的非定常气动效应延迟桨叶失速,从而产生高升力。但目前对摆线桨力的产生机制,特别是桨叶的气动力特性进行阐述的文献还很少;而摆线桨数值模拟仍在探索阶段,未来有必要继续完善,并结合PIV实验等手段对其流动机理进行详细解释。
(4)从国内外的摆线桨实验研究可以看到,目前完成的多是静拉力实验,对于前飞状态下的摆线桨气动特性了解还很少,未来需要进一步开展摆线桨相关风洞实验;而传统的螺旋桨相似理论不适用于摆线桨风洞实验,需要首先建立摆线桨的相似准则,与螺旋桨相似理论类似,需要给出的主要是:摆线桨几何相似、运动相似、动力相似、变形相似以及气动性能公式相似准则,这是设计摆线桨缩比模型风洞实验的理论基础,但目前还没有这方面研究工作的相关文献可查,值得关注。
(5)文献中关于摆线桨的一些设计参数如桨叶数、上下迎角幅值设计和翼型厚度等对气动性能影响的结论尚不一致,需要进一步分析,特别是实验验证。通过对这些设计参数进行深入研究并优化,摆线桨的气动效率还可能得到极大提高。
[1]BENEDICT M,RAMASAMY M,CHORPRA I,et al.Performance of acycloidal rotor concept for micro-air-vehicle applications[J].JournaloftheAmericanHelicopterSociety,2010,55(2):22202-1-22202-14.
[2]HU Y,LIM K B,HU W R.The research on the performance of cyclogyro[R].AIAA-2006-7704,2006.
[3]SIEGEL S,SEIDEL J,COHEN K,et al.A cycloidal propeller using dynamic lift[R].AIAA-2007-4232,2007.
[4]KIRSTEN F K.Cycloidal propulsion applied to aircraft[J].TransactionsoftheAmericanSocietyofMechanicalEngineers,1928,50(AER-50-12):25-48.
[5]WHEATLEY J B.Simplified aerodynamic analysis of the cyclogiro rotating-wing system[R].United States:National Advisory Committee for Aeronautics,1933.
[6]WHEATLEY J B,WINDLER R.Wind-tunnel tests of a cyclogiro rotor[R].United States:National Advisory Committee for Aeronautics,1935.
[7]GIBBENSR P.Construction and testing of a new aircraft cycloidal propeller[R].AIAA-1999-3906,1999.
[8]BOSCHMAJ H.Modern aviation applications for cycloidal propulsion[R].AIAA-2001-5267,2001.
[9]MCNABBM L.Development of a cycloidal propulsion computer model and comparison with experiment[D].Mississippi,Mississippi State University,2001.
[10]SIROHI J,PARSONS E,CHOPRA I.Hover performance of a cycloidal rotor for a micro air vehicle[J].Journal oftheAmericanHelicopterSociety,2007,52(3):263-279.
[11]SIROHI J,PARSONS E,CHOPRA I.Cycloidal rotor micro air vehicle[C].Proceedings of the 62ndAnnual Forum of the American Helicopter Society.Phoenix:Curran Associates,2006:18-31.
[12]BENEDICT M,SIROHI J,CHOPRA I.Design and testing of a cycloidal-Rotor MAV[C].Proceedings of the International Specialists'Meeting on Unmanned Rotorcraft.Chandler:Curran Associates,2007:404-410.
[13]BENEDICT M,CHOPRA I,RAMASAMY M,et al.Experimental investigation of the cycloidal-rotor concept for a hovering micro air vehicle[C].Proceedings of the 64thAnnual Forum of the American Helicopter Society.Montreal:Curran Associates,2008:2571-2580.
[14]BENEDICT M,RAMASAMY M,CHOPRA I,et al.Experiments on theoptimization of the MAV-scale cycloidal rotor characteristics towards improving their aerodynamic performance[C].Proceedings of the International Specialists′ Meeting on Unmanned Rotorcraft,Scottsdale:Curran Associates,2009:545-546.
[15]BENEDICT M,JARUGUMILLI T,CHOPRA I.Experimental performance optimization of a MAV-scale cycloidal rotor[C].Proceedings of the AHS Specialists'Meetings on Aerodynamics.San Francisco:Curran Associates,2010:20-22.
[16]BENEDICT M,JARUGUMILLI T,CHOPRA I.Design and development of a hover-capable cyclocopter MAV[C].Proceedings of the 65thAnnual National Froum of the American Helicopter Society.Grapevine:Curran Associates,2009:27-29.
[17]HRISHIKESHAVAN V,CHOPRA I.Design and testing of a shrouded rotor MAV with anti-torque vanes[C].Proceedings of the 64thAnnual National Froum of the American Helicopter Society.Montreal:Curran Associates,2008:28-30.
[18]BENEDICTM,CHOPRA I.Aeroelastic analysis of a MAV-scale cycloidal rotor[R].AIAA-2010-2888,2010.
[19]JARUGUMILLI T,BENEDICT M,CHOPRA I.Experimental optimization and performance analysis of a MAV scale cycloidal rotor[R].AIAA-2011-821,2011.
[20]KAN Yang,Aerodynamicsanalysis of an MAV-scale cycloidal rotor system using a structured overset RANS solver[D].Maryland,University of Maryland,2010.
[21]HWANG I S,MIN S Y,LEE C H,et al.Development of afour-rotor cyclocopter[J].JournalofAircraft,2008,45(6):25-48.
[22]HWANG I S,MIN S Y,KIM M K,et al.Multidisciplinary optimal design of cyclocopter blade system[R].AIAA-2005-2287,2005.
[23]HWANG I S,HWANG C S,MIN S Y,et al.Design and testing of VTOL UAV cyclocopter with 4rotors[C].Proceedings of the 62nd Annual Forum of the A-merican Helicopter Society.Phoenix:Curran Associates,2006:1111-1117.
[24]KIM S J,YUN C Y,KIM D,et al.Design and performance tests of cycloidal propulsion systems[R].AIAA-2003-1786,2003.
[25]NOZAKI H,SEKIGUCHI Y,MATSUUCHI K.Research and development on cycloidal propellers for airships[R].AIAA-2009-2850,2009.
[26]MATSUUCHI K,OHTSUKA N,KIMURA Y.Cycloidal propeller and its application to advanced LTA to advanced LTA vehicles[R].AIAA-2003-683,2003.
[27]NAKAIE Y,OHTA Y,HISHIDA K.Flow measurement around a cycloidal propeller[J].TheVisualization SocietyofJapan,2010,13(4):303-310,2010.
[28]IOSILEVSKII G,LEVY Y.Experimental and numerical study of cyclogiro aerodynamics[J].AIAAJournal,2006,44(12):2866-2870.
[29]IOSILEVSKII G,LEVY Y.Aerodynamics of the cyclogiro[R].AIAA-2003-3473,2003.
[30]唐继伟,胡峪,宋笔锋等.基于LB动态失速模型的摆线桨气动性能计算方法[J],飞行力学,2011,29(3):20-23.(TANG J W,HU Y,SONG B F,et al.Aerodynamics force computation method for cycloidal propeller basedon the LB dynamic stall model[J].FlightDynamics,2011,29(3):20-23.)
[31]HU Y,TANG J W,SONG B F.Aerodynamics analysis of cycloidal propeller[R].ICAS 2012-2.7.1.
[32]胡峪,唐继伟,宋笔锋.一种安装摆线桨的飞翼布局飞行器:中国,CN102556335A[P]:2012.07.11.(HU Y,TANG J W,SONG B F,et al.A cycloidal propeller flying wing aircraft:China,CN102556335A[P]:2012,07.11(in Chinese))
[33]胡峪,唐继伟,宋笔锋,等.一种摆线桨推进器:中国,CN102582830A[P]:2012,07.18.(HU Y,TANG J W,SONG B F,et al.A cycloidal propeller propulsion system:China,CN102582830A[P]:2012,07.18(in Chinese))
[34]胡峪,唐继伟,宋笔锋,等.一种摆线桨风扇:中国,CN102536862A[P]:2012,07.04.(HU Yu,TANG J W,SONG-B F,et al.A cycloidal propeller fan:China,CN102536862A[P]:2012.07.04(in Chinese))
[35]中国航空学会.首届中航工业杯-国际无人飞行器创新大奖赛获奖名单[J].航空学会通讯,2011,10:10-11.(Chinese society of aeronautics and astronautics.Win-ning entries of the first AVIC cup-international UAV innovation grand prix[J].ChineseSocietyofAeronautics&Astronautics,2011,10:10-11.)
[36]SHENG W,GALBRAITH R A,COTON F N.Amodified dynamic stall model for low mach numbers[R].AIAA-2007-626.
[37]HU Y,TAY W B,LIM K B.The analysis of cyclogyro using unsteady vortex lattice method[C].Proceedings of 25thCongress of the International Council of the Aeronautical Sciences.Hamburg:Curran Associates,2006:930-935.
[38]KATZ J,PLOTKIN A.Low-speed aerodynamics[M].Cambridge:Cambridge University Press,2001.
[39]LEISHMAN J G,BEDDOES T S.A semi-empirical model for dynamic stall[J].JournaloftheAmerican HelicopterSociety,1989,34(3):3-17.
[40]LEISHMAN J G,GILBERT L,CROUSE J.State-space model for unsteady airfoil behavior and dynamic stall[R].AIAA 89-1389,1989.
[41]SEIFERTJ.A review of the magnus effect in aeronautics[J].ProgressinAerospaceSciences,2012,55(3):17-45.
