基于波面拟合的可压缩剪切层气动光学效应分析

2013-11-09史可天马汉东

空气动力学学报 2013年6期

史可天，马汉东

（中国航天空气动力技术研究院，北京 100074）

0 引言

气动光学是研究空气动力流场对光波传输和光学成像影响的一门新型交叉学科。由于流场密度分布的时空不均匀性，平面光波通过湍流流场后，光瞳范围内不同空间位置的波面相位产生超前或滞后，从而引起成像偏移、模糊和抖动，这种现象就称为气动光学效应［1－2］。开展气动光学效应研究，探索气动流场特性与光学畸变特性之间的关联，一方面可以深入认识湍流流动机理，另一方面对提高光学成像探测系统的性能具有重要的意义［3］。

目前的气动光学传输效应研究中，已经建立了相对完善的光学畸变数值模拟方法［4－7］，但是对于光学畸变特性的深入分析，还缺乏有效的分析手段，因此难以建立光学畸变与流场特性之间的定量关联。

波面拟合是通过线性无关的基函数来拟合离散波差函数，其拟合系数可以较为明确地表达不同特性的畸变波面所产生的像差；通过对比分析各阶拟合系数的量值分布规律，还可以获取波面畸变的空间尺度特性［8］。目前，波面拟合方法多用于光学工程分析的镜面面形数据处理，在光学系统、光学设计软件和干涉检查中得到广泛应用［9－10］。

本文将波面拟合方法应用于可压缩剪切层流场气动光学效应研究，通过拟合系数定量地表达了不同波面畸变之间的差异，建立了一种光学畸变特性分析方法。对可压缩剪切层流动发展不同阶段造成的波面畸变特性进行了分析，讨论了流场结构尺度与波面畸变尺度之间的关联。

1 波面拟合方法

本文利用Zernike多项式对波面进行拟合，它在极坐标下的表达式为［11］：

其中，m、n为整数并且满足m≤n且n－m为偶数。

Zernike多项式在表述像差方面具有独特的优点，主要表现为：

（1）Zernike多项式是单位圆内的正交函数，即：

其中，m＝0时，σ＝1；m≠0时，σ＝0.5。通常的光学系统都具有圆形的光瞳，经过归一化后正好是单位圆，Zernike函数系的正交性使不同阶多项式的系数相互独立。

（2）Zernike多项式与初级像差有着一定的对应关系，第1阶反映波面整体相移，第2、3阶反映x、y方向的波面倾斜，第4阶反映离焦，第5、6阶反映不同形式的像散，第7阶至第10阶反映不同形式的彗差［8］。

（3）Zernike多项式阶数与波面畸变空间尺度有着一定的对应关系，多项式阶数越高，表达的波面畸变空间尺度越小。

假设畸变波面有M个离散数据点，光瞳口径归一化后畸变波面可以用N阶Zernike多项式表示为：

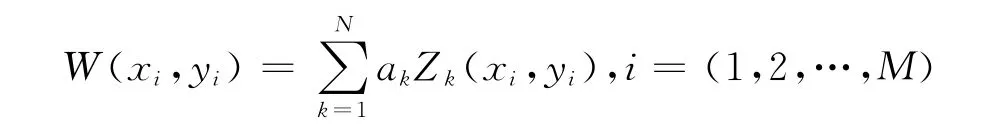
可以将上式写成矩阵形式，得到

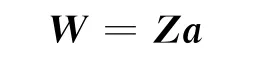
其中，Z是Zernike多项式在各离散点的取值组成的M×N阶矩阵，a是Zernike多项式的各阶系数ak组成的N维向量，W是畸变波面在离散点上的取值组成的M维向量。

通常情况下，离散点个数M大于未知系数个数N，因而方程不存在一般意义下的解，可以得到的是最小二乘解：

2 时间发展剪切层波面畸变分析

本节采用DNS方法进行了时间模式可压缩剪切层数值模拟，以获取流场的密度信息，剪切层对流马赫数Mc＝0.58。流场计算域展向和流向取周期边界条件，法向取无反射边界条件。初始流场为平均流场加扰动场，流向平均速度取双曲正切函数为初始平均速度剖面，平均法向和展向速度为零，平均温度满足Crocco－Busemann能量积分关系式，平均压力沿法向无梯度，扰动场采用最不稳定扰动波。通过线性稳定性理论分析得出最不稳定波对应x、z方向的波数α和β，计算区域取为：0≤x≤2π／α，－15≤y≤15，0≤z≤2π／β。

由于湍流的多尺度特性，本文采用了高阶紧致格式对控制方程进行空间离散，计算方法的基本思想是采用五阶精度迎风紧致格式离散N－S方程中的对流项，采用六阶精度对称紧致格式离散N－S方程中的粘性项，采用三阶Runge－Kutta方法离散时间导数项［12－13］。图1给出流场转捩过程中由瞬时压力等值面表示的Λ涡结构向马蹄涡结构的演化。

将流动发展不同时刻的法向入射波面（图2）进行拟合分析，光瞳口径为30mm。图3给出低阶拟合系数随无量纲时间的变化规律。从中可以看出与流向（本文中为x方向）相关性强的波面拟合系数增长要早于与展向（y方向）相关的拟合系数；同时，与流向相关性强的波面拟合系数增长幅值要明显大于与展向相关的拟合系数，这说明波面畸变以流向起伏为主。

图1 瞬时压力等值面Fig.1 Iso－surfaces of pressure

图2 不同时刻的波面畸变Fig.2 Wavefront distortion at different time

图3 不同时刻波面拟合低阶系数Fig.3 Coefficients of low order Zernike polynomials

在波面拟合过程中，低阶像差主要反映空间大尺度畸变，高阶像差主要反映空间小尺度畸变。从流动发展不同阶段波面拟合系数与像差阶数的对应关系（图4）可以看出，转捩过程中的拟合系数以低阶系数为主，高阶拟合系数几乎为零，这是因为转捩过程中的波面畸变主要受到流场中大尺度结构演化的影响；而转捩完成以后的高阶拟合系数则具有一定的幅值，明显大于转捩过程中的情况，这是因为转捩完成后流场中大尺度涡已经破碎成为小尺度结构，从而波面畸变具有波面起伏小幅值和空间变化频率高的特点。

图4 流动不同阶段的波面拟合系数Fig.4 Coefficients of Zernike polynomials at different flow patterns

3 空间发展剪切层波面畸变分析

受到计算条件限制，DNS计算中所取的Re数较低，虽然小尺度量已趋向各向同性，但仍未达到充分发展湍流。本节采用大涡模拟方法进行空间模式可压缩剪切层模拟，数值格式与上一小节相同，展向采用周期边界条件，法向和计算域出口采用无反射边界条件。初始流场取为平均流场加扰动场，流向平均速度取双曲正切函数为初始平均速度剖面，平均法向和展向速度为零，平均温度满足Crocco－Busemann能量关系式，平均压力沿法向无梯度，扰动场采用最不稳定扰动波。来流马赫数高速Ma1＝2.0，低速Ma2＝0.5，来流温度高速T1＝162.8K，低速T2＝279.0K，对流马赫数Mc＝0.58。

图5给出剪切层流场密度等值面，上游入口附近流场在最不稳定二维扰动下首先发生Kelvin－Helmholtz失稳，形成一系列大尺度的二维涡卷结构；随着流动的发展，相邻展向涡之间通过涡辫发生强烈的卷吸作用，导致了流动的展向失稳，二维基频涡管逐渐弯曲断裂，转捩以后的流场涡结构以较为均匀分布的三维小尺度涡为主。

图5 瞬时密度等值面Fig.5 Iso－surface of density

图6给出光瞳中心位于不同流向发展阶段时的波面光程差分布，光瞳口径取为20mm，转捩初期取在K－H失稳形成二维涡卷结构位置，转捩中期取在涡卷结构发生二次失稳的位置。图7为对应三个波面的拟合系数的幅值。为了便于比较，用波面畸变PV值对各阶拟合系数进行了无量纲化。流场转捩初期区域以二维涡卷为主要结构，因而波面畸变表现为流向的大尺度起伏，这时与展向畸变相关性强的波面拟合系数几乎为零，并且相应Zernike低阶项的拟合系数幅值明显大于高阶项系数。流动转捩区域发生二次失稳，流场结构呈现三维多尺度特性，这时对应展向和流向的拟合系数已经不存在明显的差异，虽然仍以低阶像差为主，但是其幅值有所下降，高阶像差所占的比例相对转捩初期有明显的增加，说明小尺度的波面畸变有所增长。对于完全湍流区域，流场大尺度结构已经逐步破碎成为小尺度结构，各阶拟合系数幅值相当，只有个别低阶拟合系数具有较大幅值，高阶像差在波面畸变中占有的比重进一步增大。对比图5中流场涡结构的演化特点，可以发现流场涡结构的空间分布及其尺度特性是影响波面畸变特性的重要因素。

图6 不同流向位置的波面畸变Fig.6 Wavefront distortion at different positions

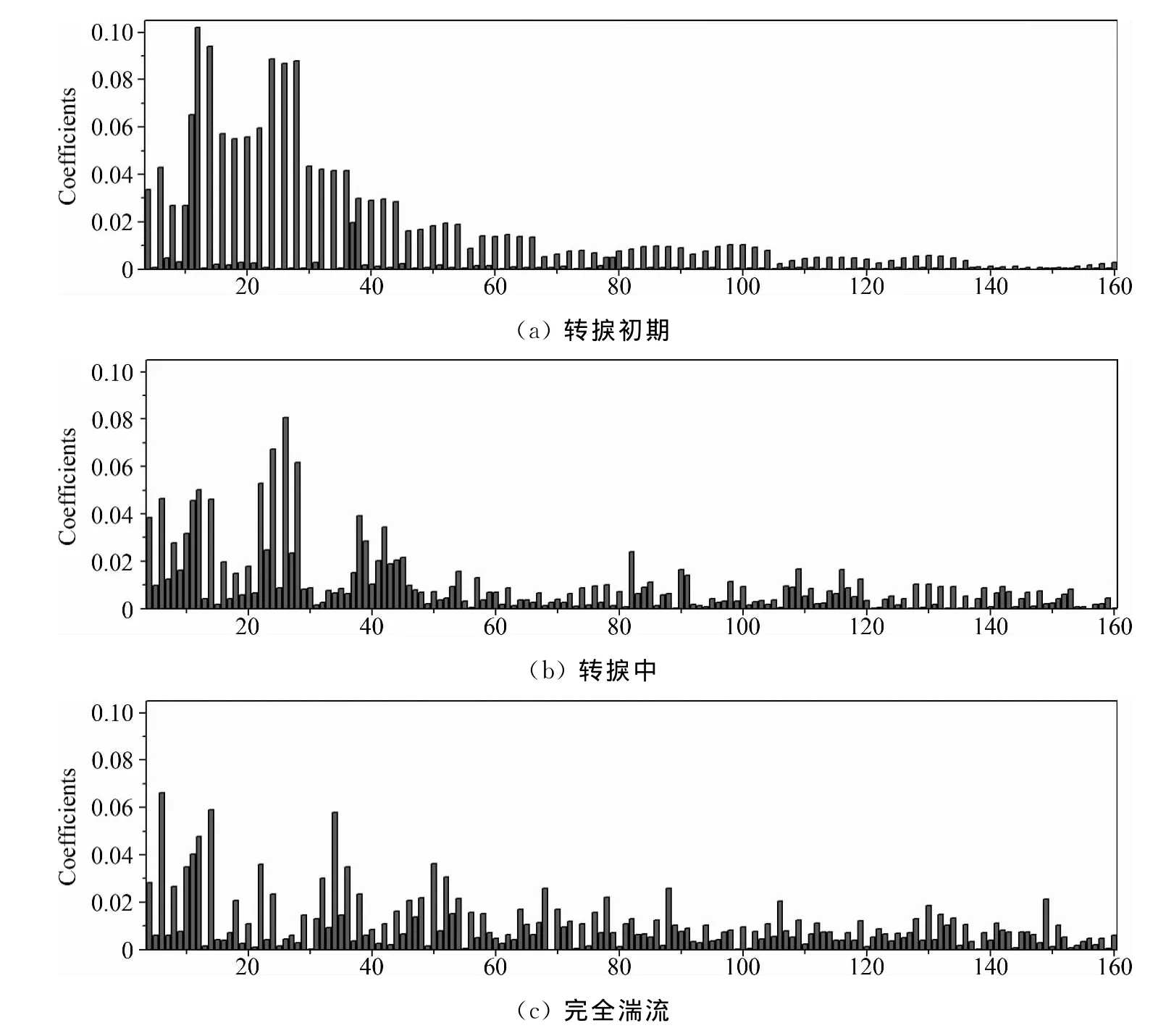
图7 不同流向位置的波面拟合系数Fig.7 Coefficients of Zernike polynomials at different positions

4 结论

应用波面拟合方法对可压缩剪切层流场引起的气动光学效应进行了分析，通过波面系数的幅值分布情况比较了流场转捩初期、转捩过程中和完全发展湍流三个阶段的波面畸变特性。分析结果表明，通过波面拟合可以定量地表达波面畸变的空间尺度特性。流场转捩初期的波面拟合系数中与流向相关的低阶系数幅值要明显大于另一个方向的系数，波面畸变以流向大尺度畸变为主，而在流场转捩过程中以及完全发展湍流区，波面拟合系数中的高阶系数幅值明显增长，波面表现为三维多尺度起伏形态。流场结构的分布特点决定了波面畸变的尺度分布特性，是可压缩剪切层流场气动光学效应的重要影响因素。

［1］SUTTON G W.Aero－optical foundations and applications［J］.AIAAJ.，1985，23（10）：1525－1537.

［2］JUMPER E J，FITZGERALD E J.Recent advances in aero－optics［J］.ProgressinAerospaceSciences，2001，37（3）：299－339.

［3］殷兴良.气动光学原理［M］.中国宇航出版社，2003.

［4］陈澄，费锦东.侧窗头罩高速层流流场光学传输效应数值模拟［J］.红外与激光工程，2005，34（5）：548－552.

［5］陈勇，郭隆德，张龙，等.带凹窗斜劈高速湍流气动光学效应研究［J］.空气动力学学报，2010，28（6）：48－53.

［6］闫溟，史可天，马汉东.针对气动光学效应的RANS计算方法研究［J］.空气动力学学报，2013，31（4）：462－465.

［7］潘宏禄，史可天，马汉东.DNS／LES方法在剪切湍流模拟中的应用［J］.空气动力学学报，2009，27（04）：444－450.

［8］田秀云，吴时彬，伍凡，等.环形大口径平面镜圆Zernike多项式拟合精度分析［J］.光学技术，2008，34（z1）：21－23.

［9］单宝忠，王淑岩，牛憨笨，等.Zernike多项式拟合方法及应用［J］.光学精密工程，2002，10（3）：318－323.

［10］NOLL R J.Zernike polynomials and atmospheric turbulence［J］.J.Opt.Soc.Am.，1976，66（3）：207－211.

［11］WANG J Y，SILVA D E.Wavefront interpretation with Zernike polynomials［J］.AppliedOptics，1980，19（9）：1510－1518.

［12］史可天，马汉东.可压缩混合层气动光学效应研究［J］.计算物理，2010，27（1）：65－72.