面向粘性流动问题的无网格/直角网格混合算法研究
2013-11-09蒲赛虎陈红全
蒲赛虎,陈红全
(南京航空航天大学 航空宇航学院,江苏 南京 210016)
0 引 言
早期数值方法采用的直角网格具有简单、规则的特点,良好的正交性避免了单元扭曲变形,因此被人们广泛使用。但处理复杂外形时,由于网格线与物面通常并不一致,在处理边界条件上存在较大困难。因此人们发展了贴体网格方法:将物理域内的曲线贴体网格映射成计算域内规则的网格,再进行求解。但是计算域内的微分方程往往比物理域内原形式更加复杂,而且曲线网格不易控制的正交性对解有较大的影响。目前,许多学者都在对直角网格方法[1]和贴体网格方法[2]进行研究和改进。
无网格方法是近年来兴起的一种新型数值计算方法,在剖分计算区域时,该方法只需要进行布点填充,而无需生成网格单元,因此具有灵活性,易于处理复杂外形。但在计算效率方面,无网格方法与网格方法相比,目前还不具有竞争性[3]。基于此,马志华等人[4]提出了一种计算区域整体采用直角网格,只在物面附近嵌入局部无网格处理的无网格/直角网格混合算法,力求无网格方法和直角网格方法的优势互补。目前该混合算法已被应用于求解Euler方程,成功模拟了鼓包、圆柱及翼型等的无粘流动[4-5],同时文献[4]展示了混合算法相对于传统网格方法在计算效率上有竞争性。
本文将无网格/直角网格混合算法发展用于求解NS方程,从而对粘性流动进行数值模拟。为了处理粘性流动问题,首先必须解决计算区域的无网格/直角网格的离散问题。对于整体直角网格,本文改用直角坐标与四叉树加密的方法生成非结构直角网格,力求通过四叉树加密等措施使网格区与无网格区过渡可控。在无网格区,本文引入了点距控制函数及无网格区之间的布点干涉机制等措施(见第2节),使得生成的点云结构能反映粘性流动边界层特点,同时适合处理多个物体相互干扰的复杂流动问题。基于计算区域的无网格直角网格离散,给出了求解NS方程耦合SA湍流模型的无网格/直角网格混合算法的具体实施方法(见第3节),编程计算了典型翼型的粘性绕流,同时成功模拟了两段翼型粘性绕流,展示了所发展的算法处理存在多个物体的粘性流动问题的可行性。
1 控制方程
本文采用的控制方程是直角坐标系下的可压缩雷诺平均NS方程,其微分形式可以写为:
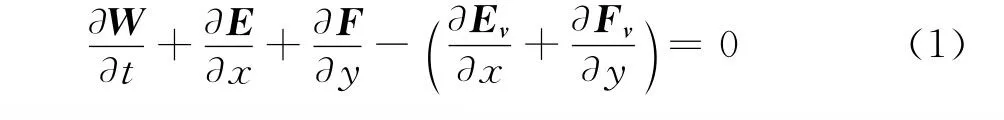
式中W为守恒矢变量,E和F为无粘矢通量,Ev和Fv为粘性矢通量,表达式如下:

Ev和Fv中的粘性应力项表达式为:
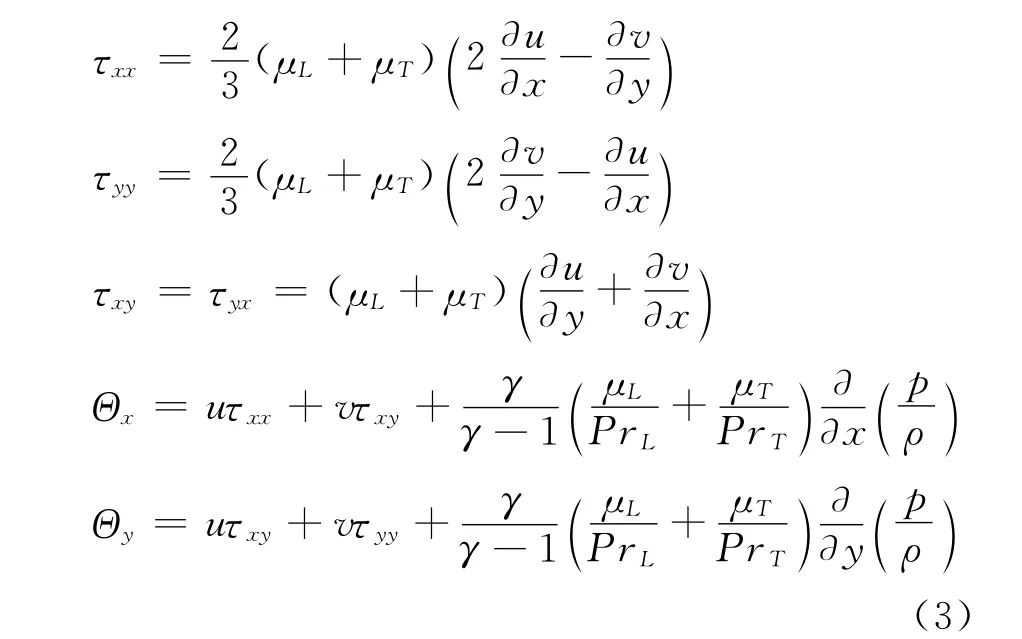
其中ρ为密度,u、v分别是沿x、y方向的速度分量,p为压强,E是单位质量内的总能。其它符号的含义可以参见文献[6]。本文层流粘性系数μL利用Surtherland公式计算得到,湍流粘性系数μT通过SA湍流模型[7]得到。
2 计算区域的无网格/直角网格离散问题
本文采用的混合算法由无网格方法和直角网格方法构成,其中无网格方法的基本计算单元称为点云。采用无网格方法,需要对计算区域进行布点离散,再对每一点构成合适的点云。图1(a)给出了一个七点无网格点云。其中i点是中心点,点1~点6是其卫星点。以函数f为例,在i点处,其空间一阶偏导数可近似为:
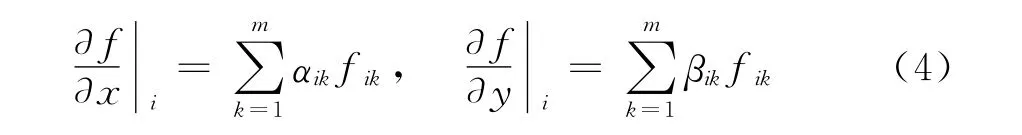
其中m表示点云中的卫星点数。fik表示i点和其第k个卫星点之间中点处的函数值。αik、βik是只与点的坐标有关的系数,在本文中,这些系数是在点云上用加权的二次极小曲面逼近如下线性方程得到:

本文沿用文献[8]的方法,对二次极小曲面逼近进行了加权,权系数形式为wik=(rref/rik)2。其中rref为i点点云的参考半径,定义为i点到其最远卫星点的距离;rik为i点与其第k个卫星点的距离。需要指出的是,对于本文粘性流动计算所涉及到的各向异性点云(图1b中所示),切向点距与法向点距之比(拉伸比)可能非常大,甚至达到100倍以上,若不采用加权(权系数wik=1),则在采用二次极小曲面逼近式(5)时系数矩阵会出现病态(比如当拉伸比为100时,系数矩阵的条件数为10000),而本文在最小二乘方法中加入上述权系数则避免了系数矩阵病态的问题,比如采用权系数后,当拉伸比为100时,系数矩阵的条件数约为4,表明系数矩阵是健康的。

图1 无网格点云Fig.1 Clouds of points for gridless method
在直角网格上,同样以函数f为例,在i点处,其空间一阶偏导数可以采用如下的差分格式逼近:
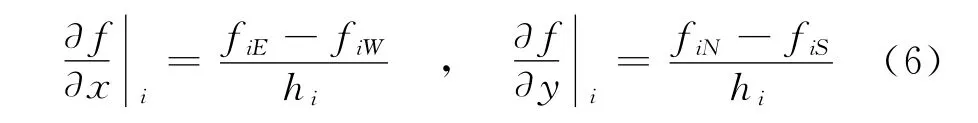
其中,hi是直角网格在i点处的网格歩长(本文生成的直角网格每一点上x方向和y方向的网格歩长相同),fiE、fiW、fiS、fiN分别是i点和其东、西、南、北方向上邻近点之间中点处的函数值。
2.1 局部无网格布点和整体直角网格生成
采用无网格/直角网格混合算法,计算区域整体采用直角网格,只在物面附近采用局部无网格处理。求解无粘流动问题时,物面附近的局部无网格通常采用图1(a)所示的各向同性点云[3,9],但对本文涉及到的粘性流动,特别是高雷诺数粘性流动而言,为了有效模拟边界层内较大的法向速度梯度,沿物面法线方向布点需较密,此时若仍采用各向同性点云,势必造成整体布点量太大,不利于减少计算时间。基于此,本文在物面附近采用了图1(b)所示的各向异性点云。采用各向异性点云,物面法线方向布点较密,从而能够模拟边界层内的法向速度梯度,而物面切线方向点距相对较大,有利于减少布点总量,节约计算时间。对单个物体,本文的布点步骤是:首先将物面边界划分成离散点的形式,然后沿物面法线方向按层推进的方法进行布点[9]。在层推进过程中,我们引入了指数函数来控制每一层点的推进距离,该函数为:

式中,di为第i层点与第i-1层点之间的距离;d1是第一层点与物面的距离,可根据计算的雷诺数由经验确定;r是一个调节距离增长速度的参数,本文取为0.1。对于流场中存在多个物体相互干扰的情况,本文在对每个物体单独采用上述方法进行布点的同时,引入了无网格区之间的布点干涉机制,以解决各个无网格区之间可能相互重叠的问题,即在对每个物体同时进行层推进布点过程中,若发现本无网格区某点周围δ距离范围内存在其它无网格区的点,则在该点处,层推进布点停止,而其它点上的层推进布点操作继续进行。δ是一个距离阀值,可根据具体计算对象确定。
在形成的无网格区中,除外边界点外,其它点的点云结构可以在布点过程中根据层推进结构同时确定,边界点点云结构的确定方法将在下节中介绍。对流场中除无网格区之外的区域,本文则采用非结构直角网格进行快速网格划分。在此过程中,我们采用了直角坐标与四叉树加密的方法生成非结构直角网格[1],采用该方法,网格区与无网格区之间过渡可控,为下一步确定网格区和无网格区交界处的点云结构打下了基础。图2中给出了GA(W)-1两段翼型周围的无网格点和非结构直角网格。
2.2 无网格区与网格区边界处点云结构的确定
采用无网格/直角网格混合算法,计算区域被分成了无网格区和网格区,这两个区之间需要进行流场信息交换。本文继承了原混合算法采用对偶节点方法实现无网格区与网格区之间流场信息交换的思想。所谓对偶节点方法,是将靠近无网格区的部分直角网格点(如图3中的方形点)作为无网格点处理,从而实现两个区之间的流场信息交换,关于该方法的细节描述可以参见文献[5]。采用对偶节点方法,需要确定直角网格区和无网格区之间边界上的点(如图3中的i点,j点)的点云结构。另外,对于多物体情况,不同无网格区之间的边界点(如图3中的k点)的点云结构也需要确定。确定某一点的点云结构,就是选择合适的点作为该点的卫星点。为此,本文提出了一种基于距离和夹角的点云选点准则,下面以图3中i点的卫星点选取过程为例,介绍该选点准则的实施过程如下:

图2 GA(W)-1翼型周围的无网格点和直角网格Fig.2 Points and Cartesian grid around GA(W)-1airfoil

图3 交界处点云结构Fig.3 Structure of the clouds of points at the interface
1)确定一个以i点为圆心,r为半径的圆形区域为选点区域,将该区域内除i点本身外的点都作为其卫星点的候选点,如图中的点1~点11。本文中r的取值为:r=k·dlocal,dlocal为i点当地的网格尺度,由网格生成过程确定。k为缩放系数,本文研究发现取1.5是一个合适的值。由于本文直角网格生成采用了四叉树数据结构,因此上述候选点可以根据既有的四叉树数据结构快速确定;
2)对于某一候选点a,分别判断由点a,中心点i和其它任意候选点b之间形成的角度α,若α<αmin(本文取αmin=30°),则比较点a和点b到中心点i的距离大小,若,则保留点a为候选点,而将点b排除出候选点;反之若,则保留点b为候选点,而将点a排除出候选点。经过上述判断,图3中的点4、点6、点7、点8就被排除出候选点范围。此步骤的作用一方面是尽量选择离中心点较近的点作为该点卫星点,另一方面避免距离太近的点以及在同一直线上的点同时作为卫星点,因为这两种情况容易造成在采用最小二乘方法确定式(1)中的系数时,系数矩阵出现病态,影响数值求解精度[10]。
经过步骤1)、2),最终剩下的候选点即作为i点的卫星点。图3中标出了采用上述方法确定的i点的点云结构,其卫星点为点1、2、3、5、9、10、11共7个点。图3同时标出了采用上述选点准则确定出来的k点的点云结构。可见采用上述选点准则,选出的卫星点围绕中心点的分布比较均匀,这有助于保证点云上空间导数的离散精度。
3 NS方程的离散及求解格式
对NS方程中的空间导数,本文在无网格区中采用式(4)进行离散,而在直角网格上采用式(6)进行离散。由于NS方程的无粘通量项与Euler方程的无粘通量项完全一样,因此本文在离散NS方程中无粘通量项时,采用了与原混合算法离散Euler方程中无粘通量项相同的方法,如在无网格区采用式(4)进行离散过程如下:
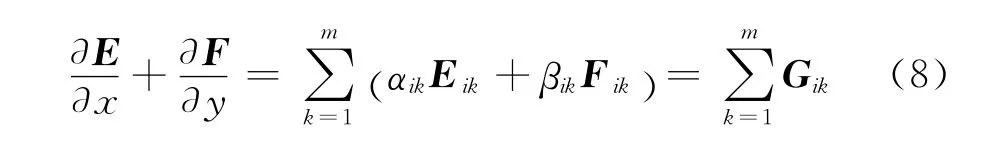
其中αik和βik是式(4)中确定的系数,Gik是i点和其第k个卫星点中点处的通量。本文与原混合算法一样,都采用Roe的近似Riemann解来确定Gik,具体过程可参见文献[4]。对于NS方程中出现的粘性通量项,以其中的项为例,本文采用无网格方法和直角网格方法进行离散的过程如下:
1)采用无网格方法离散过程:
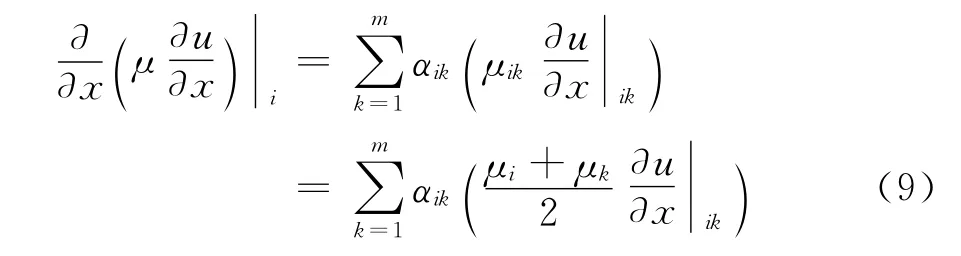
而i点和其第k个卫星点中点处的一阶导数按如下确定[8]:
其中,Δx=xk-xi,Δy=yk-yi,Δs2=Δx2+Δy2
2)采用直角网格方法离散过程:


其中而i点与其东、西、南、北四个方向上的邻近点中点处的一阶导数也采用式(10)确定。
采用无网格方法和直角网格方法离散NS方程的空间导数后,可以得到其半离散形式:

为了得到流动定常解,对于NS方程的半离散形式(12),本文采用五步Runge-Kutta显式时间推进进行处理:
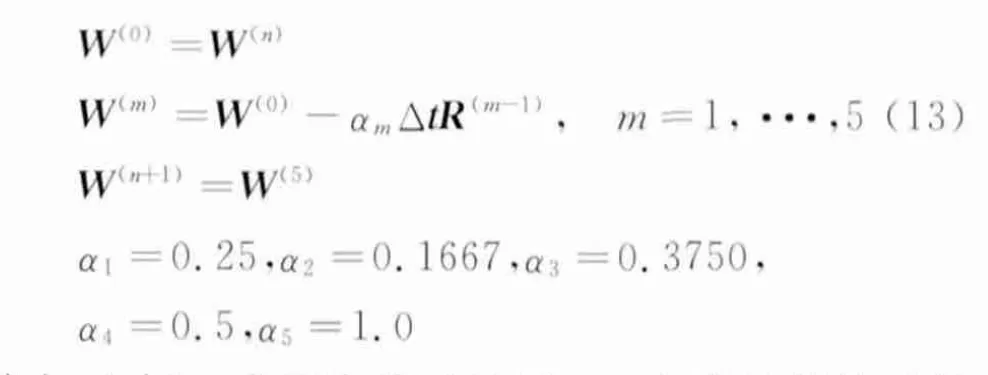
其中,上标n表示当前时间层,n+1表示新的时间层,α为歩长因子,Δt为当地时间歩长,其表达式为:

式中σ为CFL数,C为常数,本文取值为4。对于无网格方法,式中Λc和Λv的表达式如下:
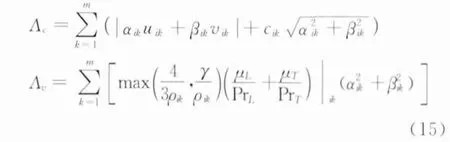
其中,uik、vik、ρik、μL、μT、cik分别表示中心点i与其第k个卫星点之间中点处的速度分量、密度、粘性系数以及音速。αik和βik为式(4)所确定的系数。在直角网格点上,当地时间歩长也可按式(14)计算得到。数值求解时还需补充边界条件,本文物面边界采用无滑移边界条件,远场则采用无反射边界条件[11]。
4 算例与分析
本文已采用发展的无网格/直角网格混合算法进行了编程,并对典型粘性流动问题进行了数值模拟。这里首先给出NACA0012翼型和RAE2822翼型的流动考核算例,在此基础上发展用于GA(W)-1两段翼型的流场数值模拟。
4.1 NACA0012翼型亚音速粘性绕流
由于有实验数据可供对照,NACA0012翼型亚音速粘性绕流计算经常用来考核算法。此算例的来流条件是Ma=0.5,α=3.51°,Re=2.93×106。本文混合算法采用的无网格点和直角网格如图4中所示,其中翼型表面布置了298个点,直角网格点和无网格点总数为20235个,第一层无网格点距物面的距离为翼型弦长的5.0×10-5倍。图5中给出了计算得到的流场等密度线分布,可以看到等密度线在网格区和无网格区之间过渡光滑(图中翼型周围的黑线是无网格区外边界),说明本文采用的两个区之间的流场信息交换方法是可行的。图6给出了翼型上表面30%弦长附近的速度型,该速度型反映出高雷诺数粘性流动边界层内速度梯度较大的特点。图7给出了计算得到的翼型表面压力系数分布,可以看到计算结果与实验数据[12]吻合较好。另外我们还对迎角较大的情况(Ma=0.301,α=9.79°,Re=2.6×106)进行了计算,图8给出了计算得到的翼型表面压力系数分布,可以看到计算结果与实验数据[12]也比较吻合。
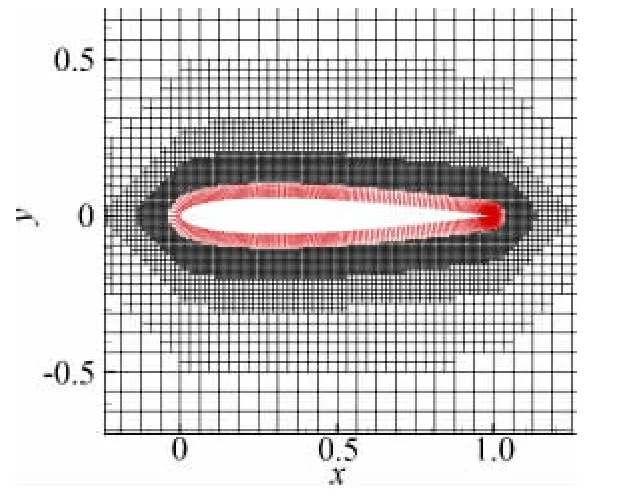
图4 NACA0012翼型周围的无网格点和直角网格Fig.4 Points and Cartesian grid around NACA0012airfoil
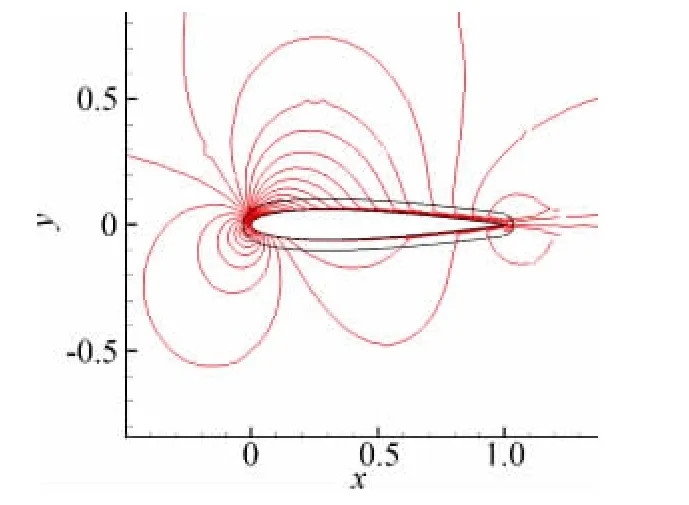
图5 流场等密度线Fig.5 Density contours of the flow field
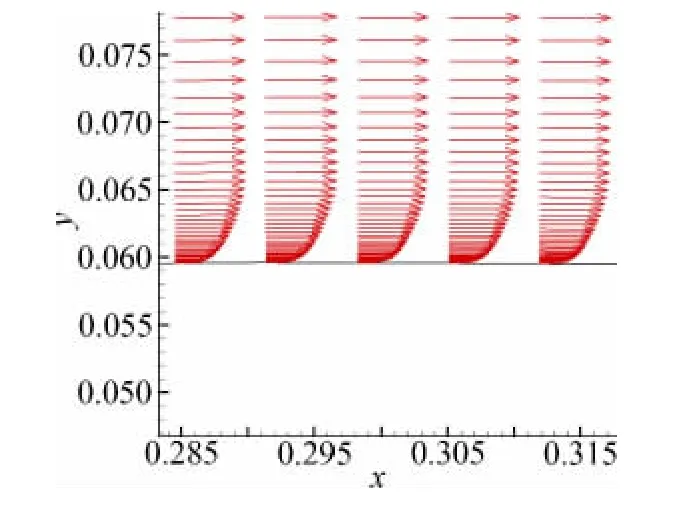
图6 上翼面速度型Fig.6 Velocity profiles near the upper surface
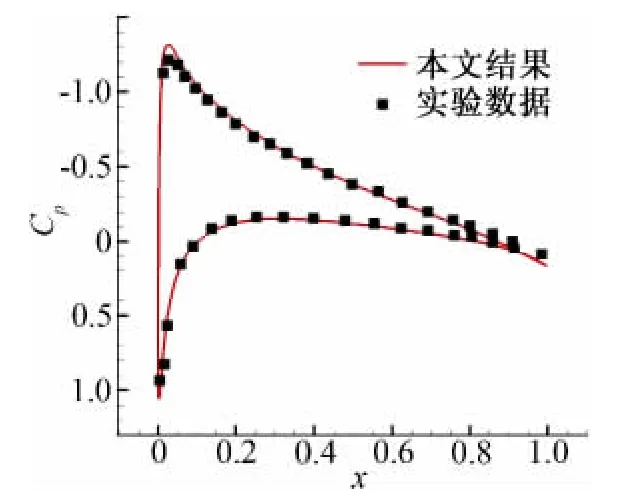
图7 迎角为3.51°时翼型表面压力系数分布Fig.7 Cpdistribution around NACA0012 with the angle of attack 3.51°

图8 迎角为9.79°时翼型表面压力系数分布Fig.8 Cpdistribution around NACA0012 with the angle of attack 9.79°
4.2 RAE2822翼型跨音速粘性绕流
上一个算例是亚音速流动问题,本算例是跨音速流动问题,用以考核所发展的混合算法对激波的捕捉能力。来流条件是Ma=0.73,α=2.79°,Re=6.5×106。图9给出了计算采用的局部无网格点和非结构直角网格,其中翼型表面布置了310个点,直角网格点和无网格点总数为23866个,第一层无网格点距物面的距离为翼型弦长的1.0×10-5倍。图10展示了计算得到的流场等密度线分布,可以看到在翼型上翼面50%弦长附近存在较强的激波,同时还可以观察到激波与边界层相互作用的情况。图11给出了计算得到的翼型表面压力系数和上翼面摩擦力系数分布,并同时给出了实验数据,可以看出计算出的激波位置和强度等主要特征与实验数据[13]吻合较好。
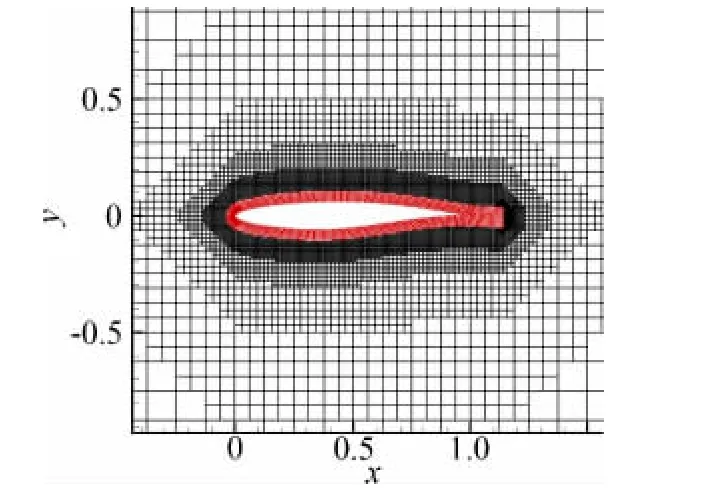
图9 RAE2822翼型周围的无网格点和直角网格Fig.9 Points and Cartesian grid around RAE2822airfoil

图10 流场等密度线Fig.10 Density contours of the flow field
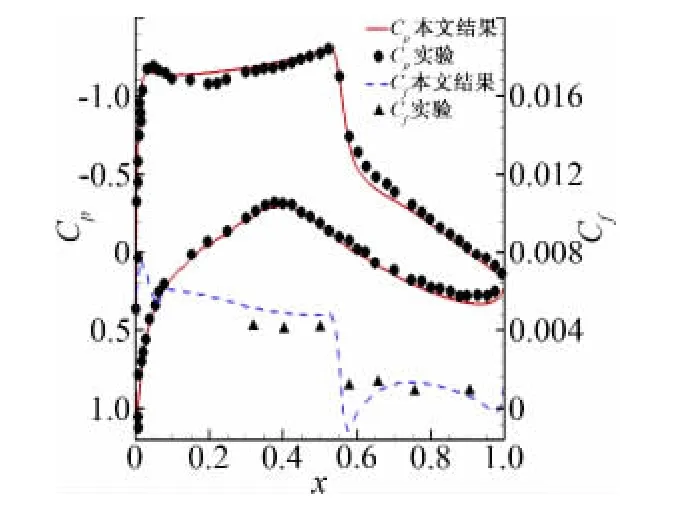
图11 翼型表面压力系数和摩擦力系数分布Fig.11 Cpand Cfdistribution around RAE2822airfoil
4.3 GA(W)-1两段翼型粘性绕流
在采用前两个算例对算法进行验证的基础上,本文还对GA(W)-1两段翼型的粘性流动进行了数值模拟。GA(W)-1两段翼型由主翼和襟翼构成,两者之间有一个狭缝。文献[2]在块对接结构网格上求解了该翼型的粘性流动问题,从该文块结构网格生成过程可以看出,对此两段翼型所在流场生成块结构网格时,需要首先根据主翼、襟翼之间的相对位置对计算区域进行分块,再在每一个块中生成结构网格,而分块操作目前还不能完全实现自动化,需要技巧。本文采用无网格/直角网格混合方法处理,不需要预先对计算区域进行分块,而是采用第2.1节中描述的方法进行无网格布点及直角网格划分,在布点过程和直角网格划分过程中不需要人工干预。图2已给出了翼型周围的无网格点和直角网格,其中主翼上布置了250个点,襟翼上布置了190个点,无网格点和直角网格点共计29768个,第一层无网格点距物面的距离为主翼弦长的5.0×10-5倍。图12给出了来流条件为Ma=0.21,α=10°,Re=2.3×106时计算得到的流场等密度线,可以看到等密度线在直角网格区和无网格区以及两个无网格区之间过渡都比较光滑。图13给出了计算得到的翼型表面压力系数分布,并与实验数据[14]和文献[2]采用块结构网格有限体积法得到的结果进行了比较,可以看出,本文结果和实验数据以及文献计算结果符合得都比较好。
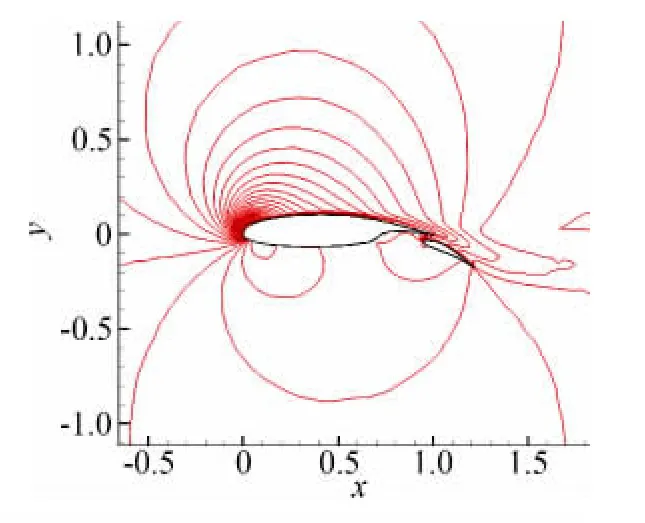
图12 流场等密度线Fig.12 Density contours of the flow field
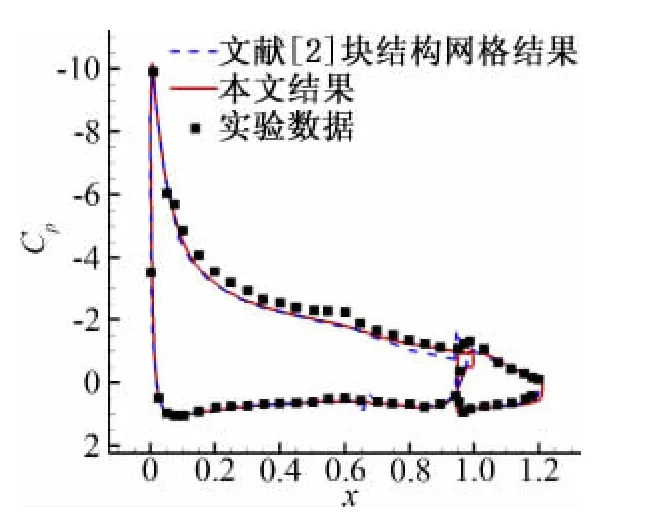
图13 翼型表面压力系数分布Fig.13 Cpdistribution around GA(W)-1airfoil
5 结 论
本文成功地将基于计算区域整体非结构直角网格物面附近局部无网格的无网格/直角网格混合算法发展用于求解粘性流动问题。采用局部四叉树加密方法生成整体非结构直角网格,实现了对流场大部分区域的快速网格划分,简化了流场计算的前置处理。算例表明:算法涉及的各向异性点云处理,能有效捕捉边界层的流动特征,捕捉的激波及边界层清晰。所发展的混合算法不仅适合处理单个翼型的粘性流动问题,也适合处理多段翼型等物体间存在相互干扰的复杂流动问题。
[1]ZEEUW D D,POWELL K G.An adaptively refined Cartesian mesh solver for the Euler equations[J].JournalofComputationalPhysics,1993,104(1):56-68.
[2]GUO T Q.LU Z L.N-S equation calculations on multielement airfoils with zonal patched grids[J].TransactionsofNanjingUniversityofAeronautics&Astronautics,2003,20(2):155-158.
[3]BATINA J T.A gridless Euler/Navier-Stokes solution algorithm for complex aircraft applications[R].AIAA 93-0333,1993.
[4]马志华.自适应无网格及网格和无网格混合算法研究[D].南京:南京航空航天大学,2008.
[5]MA Z H,EMAD N A,CHEN H Q.A local meshless method for solving comprissible Euler equations[J].SpaceResearchJournal,2008,1(1):1-16.
[6]BLAZEK J.Computational fluid dynamics:principles and applications[M].Amsterdam:Elsevier Science Ltd publisher,2001:171-173.
[7]SPALART P R,ALLMARAS S R.A one-equation turbulence model for aerodynamic flows[R].AIAA-92-0439.
[8]MORINISHI K.Gridless type solution for high Reynolds number multielement flow fields[R].AIAA 95-1856,1995.
[9]陈红全.隐式无网格算法及其应用研究[J].空气动力学学报,2002,20(2):133-140.
[10]ANG S J,YEP K S,CHEW C S,et al.A singular-value decomposition(SVD)-based generalized finite difference(GFD)method for close-interaction moving boundary flow problems[J].InternationalJournalforNumericalMethodsinEngineering,2008,76:1892-1929.
[11]阎超.计算流体力学方法及应用[M].北京:北京航空航天大学出版社,2006:252-254.
[12]THIBERT J J,GRANJACQUES M,OHMAN L H.NACA0012airfoil[R].AGARD AR 138,1979.
[13]COOK P H,McDONALD M A,FIRMIN M C P.Aerofoil RAE 2822-pressure distributions,and boundary layer and wake measurements[R].AGARD AR 138,1979.
[14]WENTZ W H,SEETHARM H C Jr.Development of a fowler flap system for a high performance general aviation airfoil[R].NASA CR-2443,1974.
