无线电能传输发射模块优化设计

冀文峰，薛卧龙，王学通，陈 莉

（河北大学，河北保定 071002）

0 引言

无线电力传输技术主要有三种：电磁感应技术、微波技术、耦合谐振技术。利用电磁感应技术可在近距离传输较大的电能而且效率较高，但是这种方法的传输距离只在1厘米之内，极大地限制了其发展。采用微波技术能够实现远距离电能无线传输，但是这种技术在能量传输过程中，要求发射器必须对准接收器，受方向性限制，且损耗大，效率低。2007年，MIT的科学家利用耦合谐振技术实现了中等距离的无线电力传输，使无线电能传输取得了突破性进展[1-5]。

现阶段，关于耦合谐振无线电力传输的理论和实验研究比较欠缺，只对耦合式无线电能传输进行了理论与实验分析[6-10]，但是发射模块与接受模块的电路模型至今没有比较完整的理论支撑及系统参数。本文以线圈为发射天线模型，分析无线电能传输的发射功率源与发射线圈之间的关系，提出提高发射效率的线圈设计方法，得到实际线圈与发射功率之间的关系，为下一步谐振耦合无线能量传输的闭环控制研究提供了借鉴依据。

1 谐振耦合电能无线传输模型

非接触式无线能量传输利用电磁感应原理实现能量传递，而谐振耦合无线电能传输是非接触式无线能量传输的一种特例，其特别之处在于：用于谐振耦合能量无线传输的2个线圈发生谐振，即线圈本身与补偿电容的高频等效电路发生谐振，而谐振时大部分能量沿谐振路径传递。谐振耦合电能无线传输装置如图1所示，一个完整的谐振耦合无线电能传输系统，包括发射电磁的发射回路，与接受电磁的接收回路，而本文主要讨论的内容为发射模块。

图1 谐振耦合电能传输原理图

2 线圈制作

2.1 电感与谐振阻抗的表达式

平面矩形的传输效率较高[11]，本文选择平面正方形圆倒角线圈作为研究对象，如图2（a）单匝矩形线圈的电感为：

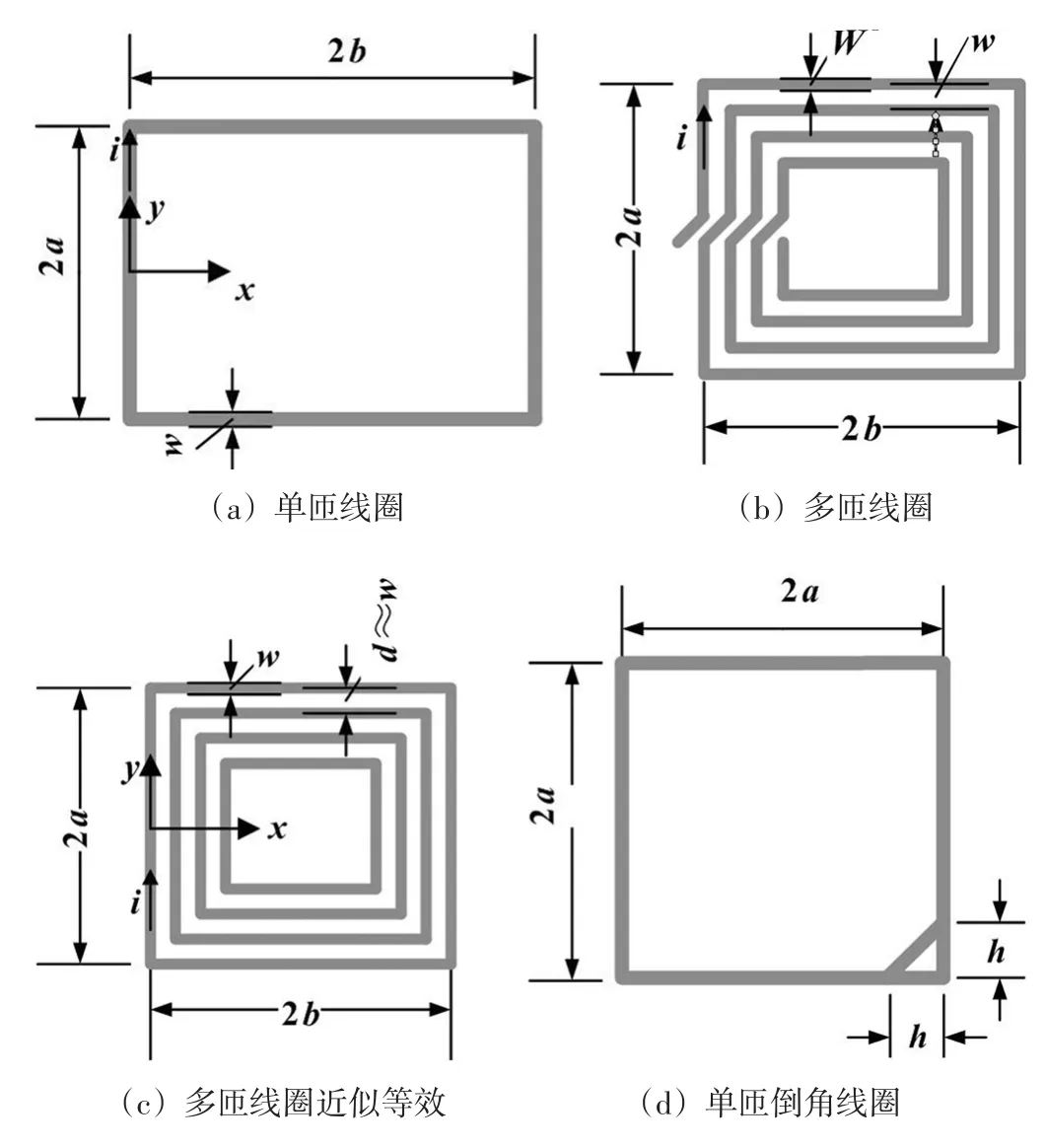
图2 线圈的模型

μ0为空气的磁导率。

多匝线圈的电感为每匝线圈的自感和匝间互感的总和，平面螺旋结构如图2（b）可以用同心线圈的方式代替，如图2（c）所示，相邻导线中心之间距离约等于线径w。假定电流所在匝的系数为p+1，另一任意线圈匝的系数为q+1，所以第（p+1）匝线圈和第（q+1）匝线圈直接的互感为：

式（2）中：

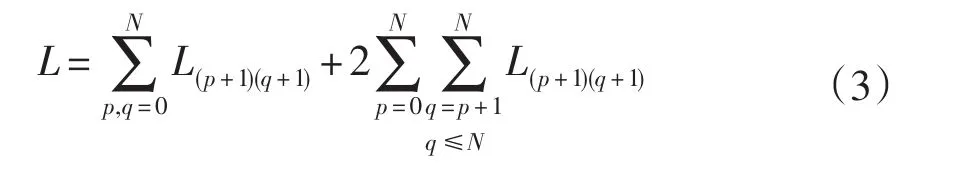
本文采取的是平面正方形倒角线圈，单匝线圈模型如图2（d）所示，其中边长为2a，已知为单匝磁通量，B为磁通密度，S为单匝线圈面积，h为倒角边长度，N为匝数，i为电流。没有倒角时：

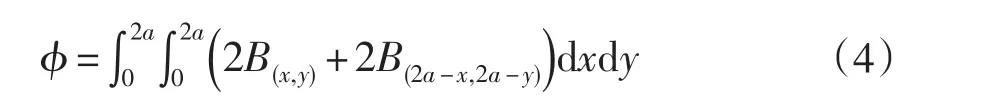
倒角部分磁通量：

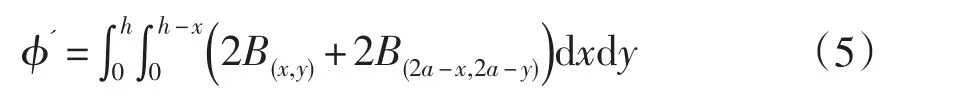
其中B(x,y)由如图3所示得到。

图3中导线在点B(x,y)产生的磁通密度为：

图3 单根导线

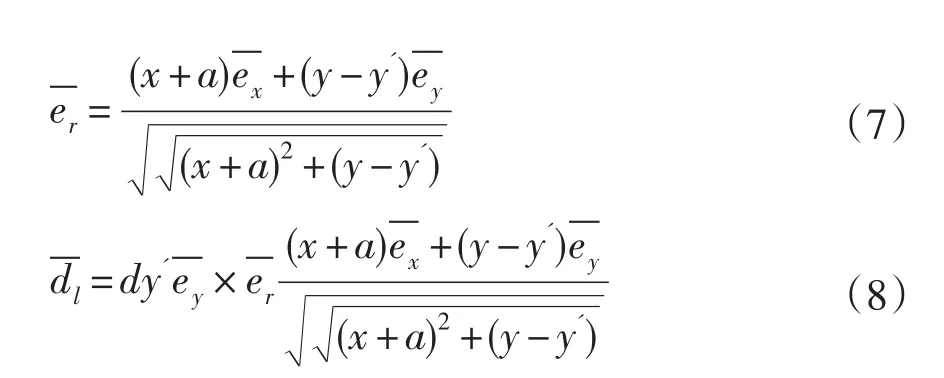
由对称原理可得线圈在点B(x,y)处的磁通密度计算公式：

得出：

用2a-x，2a-y代换x，y得出B(2a-x,2a-y)进而得到Φ和Φ'的表达式。

2.2 发射功率与线圈参数之间的关系

发射级电路主要采用S9014构成的振荡电路与MRF1550构成的功率放大电路组成。振荡电路采用电容反馈式振荡电路，设其输出阻抗为R0'，已知正方形倒角线圈的谐振负载阻抗：

其中C0为线圈的谐振补偿电容，R为线圈的直流阻抗。在得知振荡电路的输出阻抗与线圈的谐振阻抗的情况下，可根据ADS软件进行负载匹配设计功率放大电路，进而得到整体电路，完成实验目的。

由L4、C6和C9所构成的选频网络的品质因数（其中R为谐振回路的等效电阻）远大于1时，振荡频率：

对于中等距离谐振耦合的无线输电系统，其最佳自谐振频率一般1～50 MHz，由公式（13）可知：调节L1、C4和C5可得到实验需求的频率。R2和R3与三极管构成非线性限制波形幅值，故R2和R3采用滑阻，调节波形。整体电路图如图4所示。

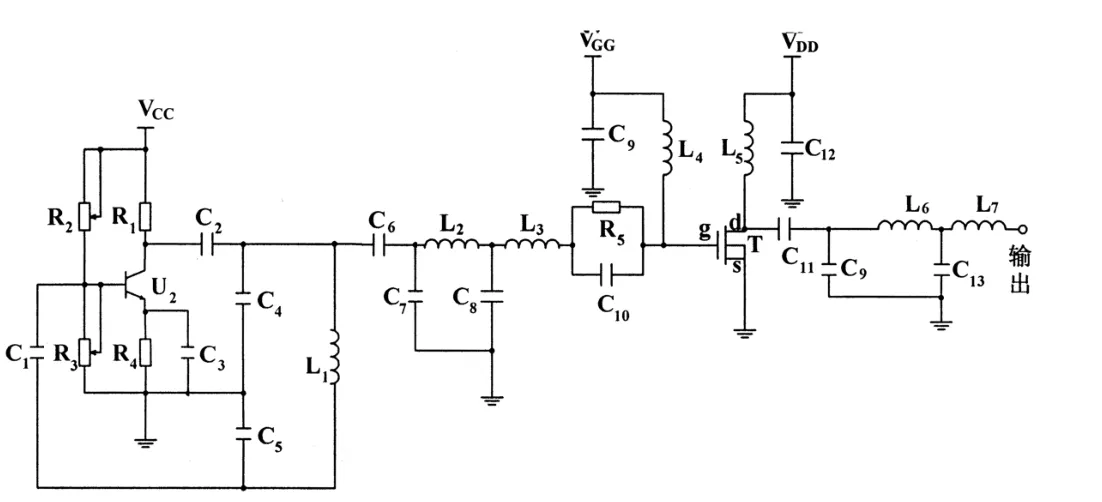
图4 整体电路图

其中功率放大部分 L2、L3、C7、C8、R5和 C10构成输入级阻抗匹配电路，C9、C13、L6和L7构成与线圈阻抗匹配电路。

3 实验结果

实验测量得线圈的电感值8.3μH，与理论计算值9.3μH比较，证明在允许实验误差的条件下，理论推导值可作为以后实验的参考与指导。

本文采用10 MHz谐振工作频率，由图5可得在误差允许条件下，振荡频率为9.993 60 MHz，空载振荡幅值最大值Vmax为1.2 V的信号源。R2和R3阻值的变化可调节放大管的偏置，从而改变放大管的工作区域，最后得到有效值为7.2 V，输出阻抗为180 Ω的振荡电路。对信号源加负载，得出输出功率与负载值的变化，测试结果如图6。

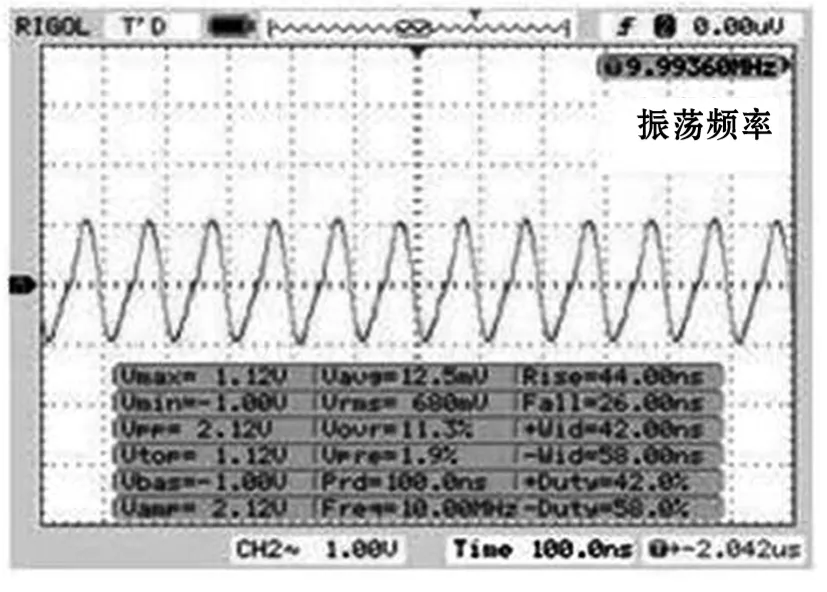
图5 振荡信号源波形

MRF1550NT1型N沟道MOSFETS，其典型工作参数：截止频率175 MHz，偏压12.5 V，最大输出功率50 W，输出功率增益14.5 dB，效率55%。

为了找到能够在已定工作频段但不具备最佳并联电容的晶体管上设计具有最优性能指标的AB类放大器方法，利用ADS软件，应用负载牵引方法，在不同输出功率、不同负载数据的条件下，找出已定频率条件下的最优值，这种方法的优点是灵活性高，根据计算机仿真找出最佳源阻抗与负载阻抗。在偏置电压VDD=15 V，VGG=2.4 V信号源输入3.8 dBm（2.4 mW）的工作条件下得出如图7所示的输出史密斯圆图，在功放输入，输出分别匹配的情况下取其中较小值。

图6 输出功率与负载关系图

图7 最大输出功率史密斯圆

4 结果及分析

最佳负载阻抗为ZL=0.637+j0.775（此阻抗为归一化阻抗，负载阻抗设为50 Ω）。最大功率为41.34 dBm。根据得出，最大功率满足实验要求。最佳负载阻抗为ZL=4.112-j2.023（此阻抗为归一化阻抗，源阻抗设为180 Ω）。最大功率为42.22 dBm，即为16.67 W，与负载最大功率相比可取其中较小值13.614 W。

5 结束语

基于耦合谐振无线电能传输是近年来研究的热点话题，本文通过对线圈和功能电路的分析，设计出工作在10 MHz频率下的发射模块，通过验证，在谐振频率下，根据线圈谐振阻抗可匹配出发射功率为13.614 W的发射电路，证明了此设计模块可为后期无线电能传输的研究做出理论和实际的借鉴。

［1］Hirai J J，Kim T W，Kawamura A.Wireless transmission of power and information for cableless linear motor drive［J］.IEEE transactions on Electronics Power，2000，15（1）：21-27.

［2］Esser A，Skudelny H C.A new approach to power sup⁃plies for robots［J］.IEEE Tra-nsactions on Applica⁃tions Industry，1999，27（5）：871-875.

［3］Manolatou C，Khan M J，Fan Shanhui，et al.Coupling of modes analysis of resonant channel add-drop filters［J］.IEEE Journal of Quantum Electronics，1999，35（9）：1322-1331.

［4］Tsang M，Psaltis D.Theory of resonantl-y enhanced near-field imaging［J］.Optical Society of America，2007，15（19）：11959-11970.

［5］Solja i M，Kurs A，Karalis A，et al.Wireless power transfer via strongly coupled magnetic r esonances［J］.Science-express，2009，112（6）：1-10.

［6］博文珍，张波，丘东元，等.自谐振线圈耦合式电能无线传输的最大效率分析与设计［J］.中国电机工程学报，2009，29（18）：21-26.

［7］博文珍，张波，丘东元.基于谐振耦合的电能无线传输系统设计［J］.机电工程，2011，28（6）：746-749.

［8］Andre Kurs，Robert Moffatt，Marin Soljacic.Simultane⁃ous mid-range power transfer to multiple devices［J］.American Institute of Physics，2010，96（4）：10-14.

［9］李阳，杨庆新，闫卓，等.磁耦合谐振式无线电能传输系统的频率特性［J］.电机与控制学报，2012，16（7）：7-11.

［10］李阳，杨庆新，陈海燕，等.无线电能传输系统中影响传输功率和效率的因素分析［J］.电工电能新技术，2012，31（3）：31-34.

［11］Jan Pannier，Dries Hendrickx，Frederik Petré，et al.Wrielesspowerteansferforindustrialapplications through steongly coupled magnetic resonances［J］.2009，29（18）：21-26.

［12］武中华，李文尧.矩形线圈自感的精确表达式［J］.物探化探计算技术，2011，33（5）：511-516.