铝合金摩擦液柱成形有限体积法数值模拟

陈 祥，闫崇京，宋 燕，房文林

(1.南京航空航天大学江苏省精密与微细制造技术重点实验室，江苏 南京 210016)

(2.南京信息职业技术学院机电工程系，江苏 南京 210016)

摩擦叠焊(Friction Stitch Welding，FSW)是一种新型的、高效的固相连接技术，可以有效地应用在飞机和飞行器的蒙皮以及结构件上裂纹缺陷的修复。由于飞机和飞行器升降过程中，舱内外的压强不断的变化，易造成金属疲劳，形成裂纹缺陷，如果不加以注意，很容易造成灾难后果[1]。目前，对于飞机和飞行器裂纹缺陷的修复常见的简便方法是铆接、螺接和补片胶接[2]，但是由于铆接和螺接容易形成应力集中区，破坏材料的连续性，所以会大大降低修补后的极限强度。而影响胶接效果的因素较多且修补的质量较低[3]。目前，搅拌摩擦焊技术虽然也可应用在飞机和飞行器部分结构件上裂纹的修复，但也只是针对较浅裂纹的情况，对于较深的裂纹，则无能为力。而摩擦叠焊技术弥补了上述修复方法的不足，焊接质量高且可以修复较深的裂纹缺陷。

作为摩擦叠焊的基础和核心，摩擦液柱成形的基本原理描述如下:在裂纹处钻出一定直径的盲孔，并制出对应的与基体材料相同的焊接棒，当摩擦叠焊的焊接棒以较高的转速并且以一定的进给速度进入盲孔，通过焊接棒与焊件之间的相互摩擦，使得焊接棒塑性化，以填充焊件缺陷部分。较长裂纹可以通过一系列摩擦液柱成形单元实现对裂纹的修补，最后通过焊件表面处理来完成焊件的整体修复任务。

但是在研究摩擦液柱成形过程中，必然涉及到该成形过程中相关参数的变化及其影响，特别是塑性化金属材料的流动速度和压力。由于金属材料的流动速度和压力难以通过一般的实验手段测得，因此需要通过有限元方法仿真出结果。相对于其他的有限元方法，有限体积法具有可以应用于不同规则网格，易于编程，适于并行，能够大大地节省计算时间等优点，所以本文采用有限体积法对铝合金摩擦液柱成形进行数值模拟。

Arora A[4]基于有限体积法，建立了搅拌摩擦焊的模型，并通过调整该模型的扭矩、功率以及焊接形状等参数，获得了该模型的传热系数和摩擦系数。陈家庆[5]等基于二维有限元模型对摩擦液柱成形初始阶段的热力耦合接触摩擦进行数值模拟，得到了焊接温度、轴向应力、转速以及径向间隙等如何影响成形过程的结论。但总体而言，国内外对此摩擦液柱成形的模拟分析还是较少，而且研究进展也多停留在二维的数值仿真上，因此深入地开展此类研究还是很有必要的。

1 数学建模的基本原理

1.1 基本定律

有限体积法是近年来发展非常迅速的一种离散化方法，其特点是计算效率高。摩擦液柱成形过程中塑性化铝合金的流动需要遵循物理守恒定律:质量守恒定律、动量守恒定律和能量守恒定律，即需要满足连续性方程、动量方程和能量方程[6]。

连续性方程的微分形式如下:

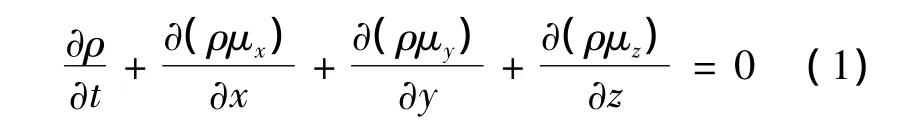
式中:μx，μy，μz分别为 x，y，z 方向的速度分量，m/s;t为时间，s;ρ为材料密度，kg/m3。

x，y和z方向的动量方程如下:

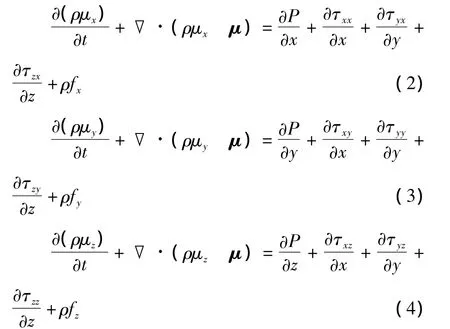
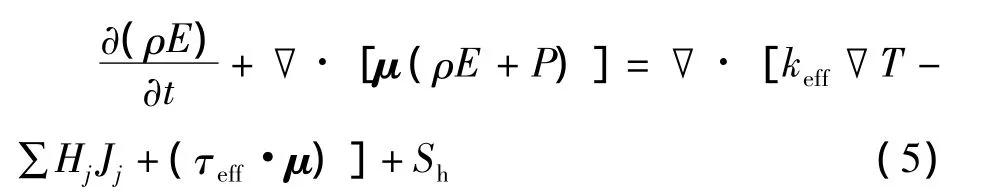
式中:E为总能，J;keff为有效热传导系数，W/(m·K);T为温度;Hj为焓，J/kg;Jj为扩散通量;τeff为有效粘性应力;Sh为其他定义的体积热源项。

1.2 迭代收敛方法

对于压力速度耦合问题，采用Simple算法。如果相邻两次迭代过程中压力和速度的修正量过大，会出现发散现象，因此需要采用亚松弛因子进行迭代，即

式中:pn－1，wn－1为上一层次计算值;p，w 为本层次计算所得未经亚松弛处理的值;pn，wn为亚松弛处理后的本层次计算值;au，aw为松弛因子，取值在0

式中:μ为速度矢量，m/s;P为塑性化铝合金的压强，Pa;τxx，τyy，τzz等为因分子粘性作用而产生的作用在微元体表面上的粘性应力的分量;fx，fy，fz为3个方向的单位质量力，m/s2。

能量方程的表达式为:到1之间。最终可以求得不同层次网格内的压力与速度值。

2 铝合金摩擦液柱成形数值模拟模型

2.1 摩擦液柱成形模型假设与边界条件设定

对于摩擦液柱成形过程而言，建立该数值模拟模型之前，首先需要定义以下几个假设条件:

a.在焊接瞬态过程中，假设焊接区域中塑性化铝合金周围的环境温度不变，此时也不考虑存在铝合金的熔化和凝固过程。

b.对于塑性化的铝合金，产生的流动设定为层流，并且被假设为单相、不可压缩的、具有一定粘度的流体。

根据德国GKSS的实验可知，在摩擦液柱成形的稳定阶段，由于在焊接一段时间后，随着焊接棒的部分铝合金塑性化和焊孔的底部部分塑性化铝合金的凝固，此时焊接棒与焊孔的形状均为圆弧形[7]。因此摩擦液柱成形三维模型设定焊接棒与焊孔为圆弧形。图1所示为摩擦液柱成形模型的截面图，AHGF为模型的静止壁面，AH和GF的长度为12mm;BCDE为模型的速度进口面，速度矢量由旋转速度和进给速度矢量合成，BC和DE的长度为9mm，BE的长度为12mm;AB和EF为模型的压力出口面，AB和EF的长度均为1mm。L1和L2分别为在该截面图选取的线段。

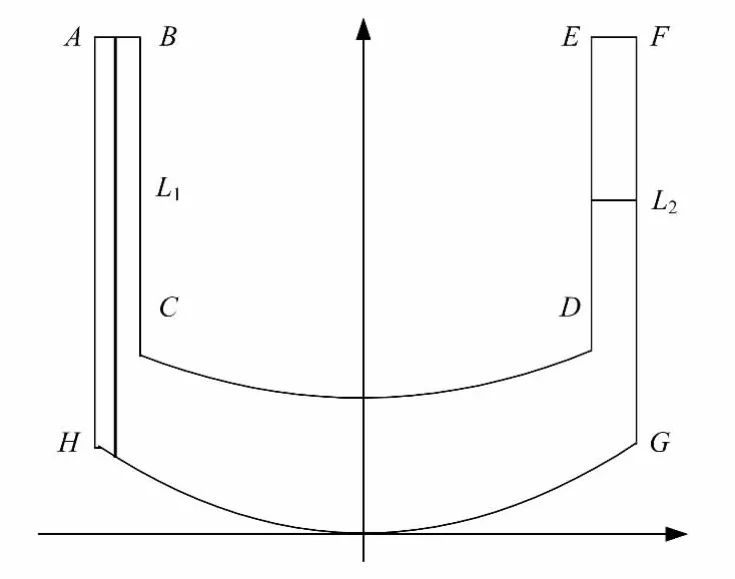
图1 摩擦液柱成形模型的截面图

2.2 网格划分与物理参数设定

图2所示为摩擦液柱成形模型的网格划分，为了消除由于网格划分导致的仿真偏差，对该模型采用统一的四面体网格划分方式，并且设定网格尺寸大小为0.05mm。

动力黏度值在流场计算中是一个比较重要的物理参数，它与温度及其应变速率均有关，通过参考陈忠海[8]在二维摩擦液柱成形中的数值模拟研究，将模拟过程中动力黏度视为常数，其值为10kPa·s，同时将进给速度和旋转速度常态值分别设置为5mm/s和5000r/min。

图2 摩擦液柱成形模型的网格划分

式中:v为材料的流动速度;D为焊接棒直径;μ为动力黏度值。在动力黏度值高达10kPa·s、铝合金的密度为2700kg/m3、铝合金的最大流动速度小于5m/s的条件下，焊接棒附近区域的雷诺数很小(约为10－3)，因此可以验证上面假设条件中塑性化铝合金的流动是层流而不是紊流。

对于雷诺数的计算，其表达式为:

3 仿真结果及分析

3.1 压力仿真结果与分析

图3为进给速度和旋转速度分别为5mm/s和5000r/min时摩擦液柱成形模型的压力分布，由图3可以看出，该模型底部的压力分布较为均匀，未出现压力突变区域。在该模型底部的压力值较高，最大值可以达到50MPa。从该模型底部到出口面的压力逐步降低，在压力出口面的压力值为0。较高压力值有利于提高摩擦的总热量，能够提高铝合金材料的塑性化程度，而且也比较有利于塑性化铝合金的爬升[9]。

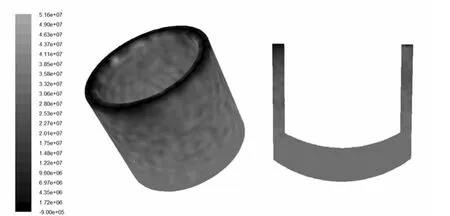
图3 摩擦液柱成形模型的压力分布

图4为旋转速度5000r/min以及进给速度值分别为 2.5mm/s、5mm/s、10mm/s 和 20mm/s 时线段L1的压力分布。在合理的进给速度范围内，进给速度较高条件下的压力值大于进给速度较低条件下的压力值。进给速度为20mm/s时，该模型底部的压力值可高达80MPa;进给速度为2.5mm/s时，压力值即使较高时也仅仅达到30MPa。在快到达压力出口面时，不同进给速度下的压力值基本重合。较高的进给速度则意味着塑性化铝合金向上爬升的速度也较快，此时需要较高的压力值来减小由于高黏度所带来的阻力，以保证铝合金的爬升速度。同时，较高的爬升速度，将会导致沿程压力损失较大，因此当进给速度为20mm/s时，相对于其他的进给速度而言，压力下降比较快。

图4 不同进给速度时线段L1的压力分布

图5为进给速度5mm/s以及旋转速度分别为3000r/min、4000r/min、5000r/min 和 6000r/min时线段L1的压力分布。旋转速度为3000r/min时，该模型底部压力值接近30MPa，而旋转速度为6000r/min时，该模型底部压力仅仅约为40MPa，因此提高旋转速度只是略微增加压力，所以旋转速度对压力分布的影响小于进给速度的影响。

图5 不同旋转速度时线段L1的压力分布

3.2 速度仿真结果与分析

图6为摩擦液柱成形模型的流线图，由图6可以看出塑性化铝合金材料的流动轨迹，同时还可以看出，铝合金材料的流动主要是绕焊接棒进行旋转，而流线向上爬升分量非常小。模型的流动速度表达式为:

式中:v旋为旋转速度;v进为进给速度;n为转速。

在旋转速度为5000r/min、进给速度为5mm/s和焊接棒直径为9mm的条件下，v旋的最大值约为2.5m/s。对于由进给速度和旋转速度合成的矢量流动速度而言，除了模型底部中心轴附近区域外，显然旋转速度远大于进给速度。因此，铝合金材料的流动速度基本上与旋转速度成正比。

图6 摩擦液柱成形模型的流线图

图7为旋转速度5000r/min和进给速度5mm/s时摩擦液柱成形模型的流动速度分布，由图7可以看出，焊接过程中流动速度较大的区域主要集中在旋转壁面附近，该模型的流动速度最大值约为2.6m/s。由筒壁区域中线段L2的流动速度分布情况可以看出，流动速度的分布从旋转壁面到焊件的静止壁面，流动速度的分布是呈线性递减。这是因为当铝合金材料的黏度值是定值时，速度梯度也为定值，因此筒壁区域的流动速度呈线性分布。

图7 摩擦液柱成形模型的流动速度分布

由图7还可以看出该模型底部流动速度分布的基本情况:在该模型的底部的两端和中心轴附近的流动速度较慢，塑性化铝合金材料的流动较慢，这是由于在中心轴附近旋转速度较慢，所以导致流动速度较慢。而在底部两端处，由于离旋转壁面较远，在高的黏度值下，造成两端流动速度快速下降。在焊接起始阶段需要注意的是，该模型底部两端处的焊接温度较低，铝合金塑性化不够彻底，因而造成材料流动较慢，而且该处在焊接时与空气有接触，容易产生氧化物，所以是比较容易形成焊接缺陷的区域[10－12]。

4 结束语

本文基于有限体积法建立了单相、层流、不可压缩的铝合金三维摩擦液柱成形的模型。摩擦液柱成形的过程被模拟为经过在包含旋转速度和进给速度的影响下铝合金流体的流动瞬态过程，获得了铝合金材料流动速度分布和压力分布。相对于二维有限元模型而言，三维模型更符合摩擦液柱成形的实际情况，具有更高的可信度。通过研究摩擦液柱成形的数值模拟过程，优化摩擦液柱成形的工艺参数，为工程实践提供指导。

[1] 吴昊.民用飞机规划维修技术理论及应用研究[D].南京:南京航空航天大学，2009:4－11.

[2] 李艳，焦良，于克杰.补片尺寸对胶补飞机蒙皮强度的影响[J].航空维修与工程，2008(2):38－39.

[3] 舒茂盛.飞机壁板战伤修补方法的数值研究[D].西安:西北工业大学，2005:24－27.

[4] Arora A，Nandan R，Reynolds A P，et al.Torque，power requirement and stir zone geometry in friction stir welding through modeling and experiments[J].Scripta Materialia，2009，60(1):13－16.

[5] 陈家庆，焦向东，邱宗义，等.摩擦液柱成形初始阶段的二维轴对称数值模拟[J].中国机械工程，2008，19(23):2867－2872.

[6] 赵衍华，林三宝，贺紫秋，等.二维搅拌摩擦焊接过程的数值模拟[J].中国有色金属学报，2005，15(6):865－869.

[7] Meyer A.Friction Hydro Pillar Processing Bonding Mechanism and Properties[D].Geesthacht:GKSS－Forschungszentrum Geesthacht GmbH，2003:103－113.

[8] 陈忠海，陈家庆，焦向东，等.摩擦液柱成形过程的二维CFD数值模拟[J].石油化工高等学校学报，2010，23(1):55－59.

[9] Hattingh D G，Bulbring D L H，Els－Botes A，et al.Process parameter influence on performance of friction taper stud welds in AISI 4140 steel[J].Materials and Design，2011，32(6):3421－3430.

[10] 高辉.摩擦叠焊试验装置及焊接工艺研究[D].北京:北京化工大学，2010:37－69.

[11] 高辉，焦向东，周灿丰，等.预热对LY12铝合金摩擦叠焊质量的影响[J].上海交通大学学报，2010，44(增刊1):70－76.

[12] Chludzinski M，Paes M P，Bastian F L，et al.Fracture toughness of friction hydro－pillar processing welding in C－Mn steel[J].Materials and Design，2012，33(1):340－344.