六轮磁吸附爬壁机器人铅垂壁面滑移转向点到点路径规划

杨闫景，钱瑞明

(1.93511部队，山西 代县 034200)

(2.东南大学机械工程学院，江苏 南京 211189)

磁吸附爬壁机器人是一种利用永磁体吸附在导磁壁面上进行特定作业的自动化机械装置，它在造船业、核工业、石化工业等铁磁性结构的环境中受到愈来愈广泛的应用，可以代替人类完成除锈喷漆、探伤检测、加工焊接等工作[1]。

由于爬壁机器人工作于壁面的特殊性，其动力学问题对机器人的结构设计、运动控制和路径规划有着重要意义。衣正尧等提出了履带式爬壁机器人铅垂壁面滑移转向的动力学模型[2]，钱志源等建立了双轮差速驱动爬壁机器人的动力学模型[3]，李志海等提出了四轮差速驱动爬壁机器人的动力学模型[4]。田蓝图分析了履带式爬壁机器人运动学仿真问题[5]，张俊强提出了履带式机器人平面路径规划方案[6]。轮式爬壁机器人应用广泛，但其支撑力分布、驱动轮摩擦状态因车轮数量的不同而模型不同，且针对四轮或多轮爬壁机器人路径规划问题的研究文献目前较少。

本文针对一种六轮磁吸附爬壁机器人，基于车轮触地点的速度分析和车辆力平衡关系，对其在铅垂壁面作业时的滑移转向过程进行动力学建模，研究爬壁机器人车辆的转向轨迹并提出点到点的路径规划方案，为该类机器人的运动控制和应用提供理论依据。

1 铅垂壁面滑移转向动力学模型的建立

1.1 随车坐标系下滑移转向模型的建立

图1所示为六轮磁吸附爬壁机器人车辆(以下简称为车辆)在铅垂壁面上绕瞬时转动中心C作滑移右转向的一个状态，车辆的位姿用随车坐标系xaoaya的原点在壁面全局坐标系XOY中的坐标(Xa，Ya)和xa轴至X轴的夹角θ表示，其中坐标系xaoaya的原点取为车辆两后轮中心连线的中点。设车轮与壁面间为有摩擦点接触，第i车轮自转转速为ωi(俯视向前旋转为负)，车轮半径均为R，第i个车轮中心Pi在随车坐标系中的坐标为(xi，yi)，转动瞬心C在随车坐标系中的坐标为(xC，yC)，车辆瞬时转向角速度为ω(逆时针方向为正)，CPi与 xa轴的夹角为 αi，CPi的长度为L(Pi，C)。其他参数如图1所示。

如图1，第i车轮上触壁点相对于车体的速度为vi=Rωi，第i车轮中心Pi相对全局坐标系的绝对速度为 vir=L(Pi，C)ω，其方向垂直于 CPi，vir与 xa轴的夹角为αir。车轮触壁点相对全局坐标系的绝对速度vid为vi和vir的合成，vid与xa轴的夹角为αid，轮1的上述参数描述如图2所示。

以车轮1为例，对其进行速度分析，可得:

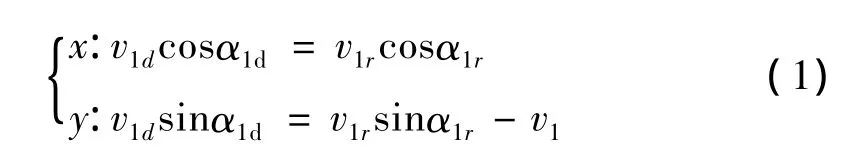
由图2可知，α1d位于第一象限，整理式(1)可得:

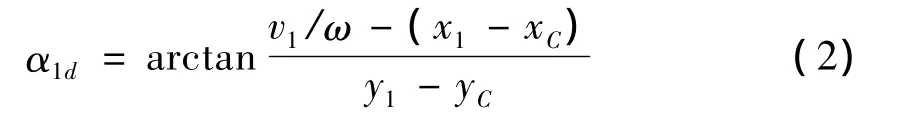
图1 六轮车辆铅垂壁面滑移转向模型

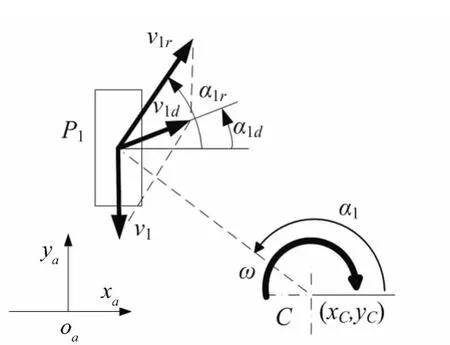
图2 轮1速度分析

触壁点处的滑动摩擦力方向与滑动速度方向相反，即轮1上触壁点处滑动摩擦力与xa轴夹角为方向角α1f=α1d+π。同理根据αid所在象限即可求得其余车轮摩擦力方向角αif。

设车辆总质量为m，重力(G=mg)与xa轴的夹角为αG=3π/2－θ;质心S在随车坐标系中的坐标为(xS，yS)，质心瞬时转动半径 r=L(S，C)，质心相对全局坐标系的绝对速度(vS=rω)与xa轴的夹角为αvS=arctan((yS－yC)/(xS－xC))，质心相对全局坐标系的绝对加速度avS与xa轴的夹角为αa;车辆相对全局坐标系的绝对转动角加速度为aω，绕质心转动惯量为IS。则滑移转向时的车辆动力学方程[7－8]为:

式中:摩擦力Ffi=μNi，Ni为壁面对第i个车轮支撑力，μ为车轮与壁面间的滑动摩擦系数(设为定值)。

1.2 壁面对车轮支撑力模型

当车辆处于静态吸附状态时，各车轮所受壁面支撑力满足下式:

式中h为质心高度。

机器人处于运动状态时，各车轮所受支撑力分析如下[4]:当各磁轮对壁面的磁吸附力均为Fm，且仅考虑磁吸附力作用时，各车轮上由磁吸附力产生的支撑力相等，即磁轮i所受支撑力为N(1)i=Fm，i=1，2，…，6。同时需满足6μFm＞ G。

假定在沿xa轴方向的重力分量GcosαG和沿该方向的惯性力分量mavScosαa的合力作用下，车轮所受的支撑力沿xa轴方向符合线性分布，则各车轮所受支撑力为:

式中xn为在随车坐标系下支撑力等零的分界线x轴坐标。因为同侧车轮的xa轴坐标相同，所以上式可以简化为:

式中:下标 l为第1，2，3 车轮，下标 r为第4，5，6 车轮。

假定在沿ya轴方向的重力分量GsinαG和沿该方向的惯性力分量mavSsinαa的合力作用下，车轮所受的支撑力沿ya轴方向符合线性分布，则各车轮所受支撑力为:

式中yn为在随车坐标系下支撑力等零的分界线。

车辆在磁吸附力、沿xa轴方向的合力和ya轴方向的合力的综合作用下，各车轮所受壁面支撑力分别为3个力分别作用下各车轮支撑力的合力，用下式表示:

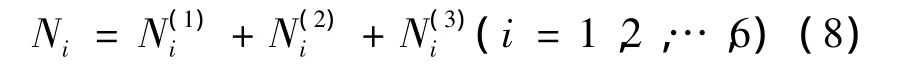
将其代入式(5)，经MATLAB数值计算验证，结果相符合。运动过程中应满足Ni＞0，即保持车轮始终与壁面接触。

1.3 全局坐标系下滑移转向模型的建立

车辆在铅垂壁面运动时，车辆倾斜角度θ影响转动瞬心位置，车体和转动瞬心时刻都在变化，需要建立随车坐标系在全局坐标系中的变化关系。为简化计算，假定车辆在由初始位置E1转动微角度dθ至终点位置E2过程中，其瞬心不发生变化。

已知车辆初始位置E1处随车坐标系原点的全局坐标(XE1，YE1)和倾斜角度θE1，同侧车轮的转速取为相等，车辆逆时针转向dθ角度后，求解终点位置E2处随车坐标系原点的全局坐标的步骤为:

a.根据式(3)～(8)求得E1处随车坐标系下的转动瞬心坐标(xC，yC)。

b.根据坐标转换求出瞬心全局坐标 (XC，YC)。

c.建立原点为转动瞬心的瞬心坐标系xbobyb，求出车辆随车坐标系原点在瞬心坐标系里的坐标(xE1b，yE1b)。

d.根据刚体转动坐标转换，在瞬心坐标系下求得随车坐标系原点绕转动瞬心旋转微角度dθ后的 E2处的坐标(xE2b，yE2b)。

e.根据瞬心坐标系和全局坐标系的转换规则，求得E2处随车坐标系原点的全局坐标(XE2，YE2)，车辆倾斜角度为(θE1+dθ)。

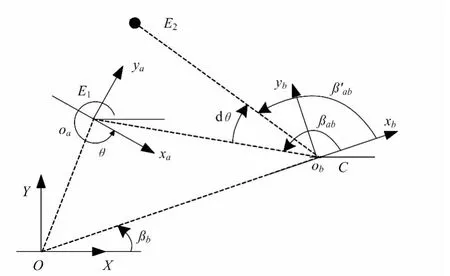
图3 随车坐标系在全局坐标系中的变化关系

图3中，θ为车辆倾斜角度，E1为车辆初始位置，E2为车辆绕瞬心C转动微角度dθ后的终点位置。坐标系xbobyb为瞬心坐标系，其原点为瞬心C，其x轴方向为全局坐标系原点O与瞬心C连线的延长线，βb为xb轴与X轴夹角。βab为射线CE1与xb轴夹角。根据随车坐标系相对全局坐标系的转换，可知瞬心C的全局坐标为:

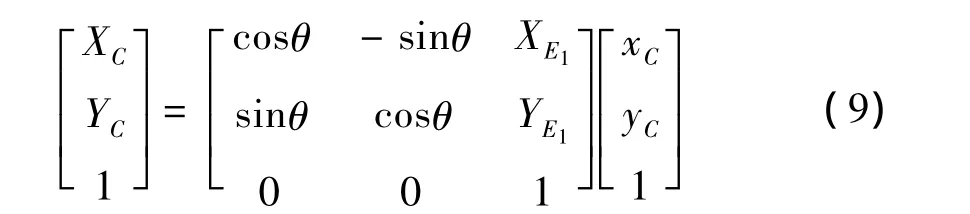
式中 tanβb=YC/XC，可得 βab和，可得，根据坐标系xbobyb对坐标系XOY的转换，可知E2处的随车坐标系原点的全局坐标为:

在瞬心坐标系xbobyb中:

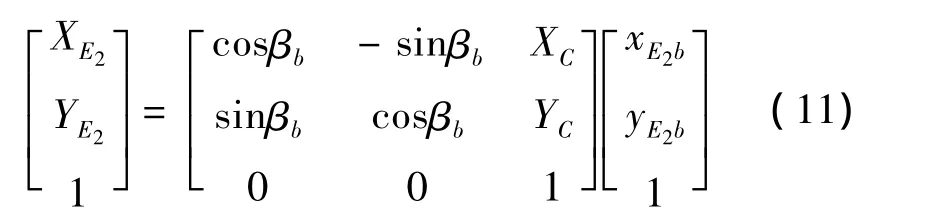
质心加速度avS及其与X轴角度αa为:

式中vSE1，vSE2和αvSE2，αvSE2为质心速度及其与 X轴夹角。

2 车辆轨迹分析

六轮车辆原始参数见表1，IS为车辆质心转动惯量。假定当θ=0时，初始位置位于全局坐标系原点处，即随车坐标系原点的全局坐标为(Xa，Ya)=[0，0]。当车辆左右两侧车轮转速[ωl，ωr]分别等于[－16.7，16.7]和[16.7，－16.7]时，将上述参数代入式(3)～(11)，经MATLAB数值求解可求得随车坐标系原点顺时针和逆时针分别转向一周后的全局坐标轨迹。如图4(a)，曲线1为车辆顺时针转向轨迹(终点处θ=－2π)，曲线2为车辆逆时针转向轨迹(终点处θ=2π)，圆心为随车坐标系原点，直线为车身，“+”为车辆质心。图4(b)为ADAMS模拟中车辆顺时针转向轨迹，与图4(a)中理论轨迹曲线1相同。可以看出，车辆因为重力的原因，轨迹呈不规则曲线。顺时针转向和逆时针转向呈现对称关系，顺时针转向呈左下降趋势，逆时针转向呈右下降趋势。

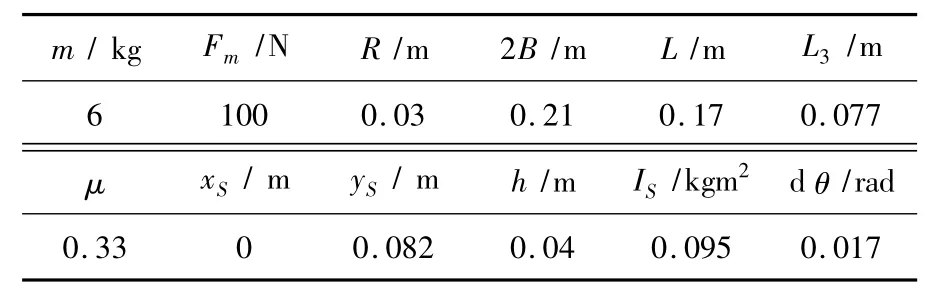
表1 六轮车辆原始参数

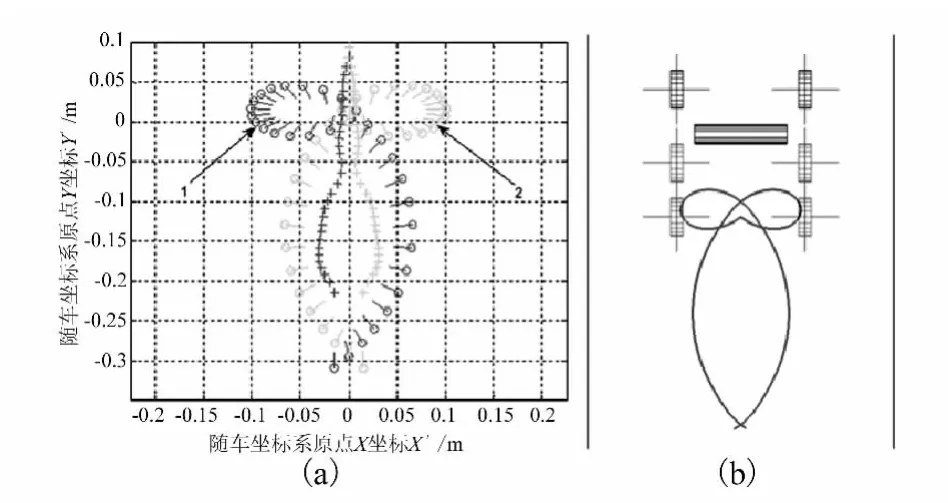
图4 车辆顺时针和逆时针转向时的原点和质心轨迹

进一步计算表明，此轨迹x轴方向与左右侧车轮转速比有关，y轴方向与重力和总磁吸附力之比有关;当爬壁机器人车辆同侧车轮的转速取为相等时，则难以使其在铅垂壁面实现原地旋转或绕某点做圆周运动。

3 路径规划

3.1 路径规划方案

因车辆两侧车轮转速选择的不同，由初始位置到目标位置可以有多种路径规划方案。为简化路径分析，假定路径规划中，车辆同侧车轮的转速取为相等，左右两侧车轮的转速大小相等，方向相同或相反，即车辆只能直线前进或后退、顺时针或逆时针转向。

设车辆初始位置为B(XB，YB)、θ=φ，目标位置为M(XM，YM)、θ= γ⊂[φ－2π，φ)，通用路径规划如图5所示，图中实线为规划路径，虚线为图4中的车辆顺时针和逆时针转向轨迹，圆弧实线箭头为E1运动方向。

图5 铅垂壁面通用路径规划

当γ⊂[φ－2π，φ－π)时，路径方案为图5(a)，步骤如下:

a.根据图4(a)曲线1获得车辆在初始位置θ=φ时的局部坐标(xB，yB)，并以此建立局部坐标系xoy。将全局坐标M(XM，YM)转换为局部坐标系xoy中的(xM，yM)=(XM+xB－XB，YM+yB－YB)。

b.根据图4(a)获得车辆原点在曲线1中θ=γ时的局部坐标M'(a，b)，可求得线段M'M与x 轴夹角 γ'。

c.顺时针转向至车辆车身平行于M'M的F点。

d.改为直线运动，方向为线段M'M方向，运动距离为 L(M'，M)，至点 F'。

e.继续顺时针转向至θ=γ，终点即为目标位置M。

当γ⊂[φ－π，φ)时，使γ =γ+2π，路径方案为图5(b)。方案为将上述步骤中的曲线1改为曲线2、顺时针转向改为逆时针转向即可。

图5中，每次车辆转向角度均大于π，耗时较长，研究发现特定条件下其路径可简化。以目标位置M(XM，YM)、θ= γ，γ⊂[φ－π，φ)为例，车辆路径规划为:

a.根据图4(a)曲线1获得车辆在初始位置θ=φ时的局部坐标(xB，yB)，并以此建立局部坐标系xoy。将全局坐标M(XM，YM)转换为局部坐标系xoy中的(xM，yM)=(XM+xB－XB，YM+yB－YB)。

b.根据图4(a)确定曲线1中θ=γ时的局部坐标M2(a2，b2)，可知线段M2M与x轴夹角 γ'。如果γ'＞γ+π/2，γ+π/2为车身方向角度，则符合简化路径规划条件，进入步骤c，否则不符合。

c.顺时针转向，至车身方向平行于M2M。

d.改为直线运动，方向为线段M2M方向，距离为 L(M2，M)，至点 F'。

e.继续顺时针转向至θ=γ，终点即为目标点M。

其简化路径如图6(a)所示。可以看出车辆在第一段转向中，未经过M2点;如果步骤a中经过M2点，即γ'＜γ+π/2，则此简化路径方案不能适用。

图6 铅垂壁面简化路径规划

同理可得当目标点γ⊂[φ－2π，φ－π)时的简化方案:使γ=γ+2π，将上述简化方案中的曲线1改为曲线2，顺时针改为逆时针，小于号与大于号互换即可，如图6(b)所示。

3.2 路径规划实例

设车辆初始位置为B(0，0)点，θ=φ =0;目标位置M(XM，YM)=(0.4，0.2)，θ= γ =－π。其路径规划中，首先判断其是否适用简化路径方案，可以则采用，否则采用通用路径规划方案。

目标位置θ=－π⊂[－π，0)，在顺时针转向轨迹中，路径规划步骤为:

a.根据图4(a)曲线1获得车辆在初始位置θ =0时的局部坐标(xB，yB)=(0，0)，并以此建立局部坐标系xoy。将全局坐标M(XM，YM)转换为局部坐标系xoy中的(xM，yM)=(XM+xB－XB，YM+yB－YB)=(0.4，0.2)。

b.根据图4(a)确定曲线1中θ=－π时的局部坐标 M2(a2，b2)=(－0.007，0.029)，可知线段M2M与x轴夹角γ'=arctan((yM－b2)/(xM－a2))=0.4＞γ+π/2=－π/2。符合简化路径规划条件，进入步骤c。

c.顺时针转向，至车身方向平行于M2M。

d.改为直线运动，方向为线段M2M方向，距离为 L(M2，M)，至点 F'。

e.继续顺时针转向至θ=γ，终点即为目标点M。其路径轨迹如图7所示。

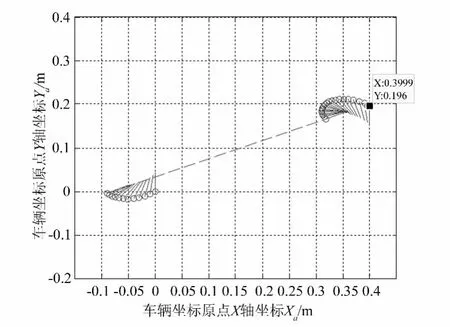
图7 车辆路径规划实例

根据dt=dθ/ω可得车辆两侧车轮转速随时间变化如图8所示。“o”型曲线为左侧车轮，“+”型曲线为右侧车轮。

图8 左右侧车轮角速度变化规律

在ADAMS中模拟爬壁机器人路径规划如图9所示，可以看出其轨迹与图7理论轨迹相同，ADAMS模拟达到预期目的。

图9 车辆在ADAMS中路径规划模拟

4 结束语

本文基于车轮触地点的速度分析和车辆力平衡关系建立了六轮爬壁机器人车辆铅垂壁面作业时的滑移转向动力学模型。根据此模型获得了爬壁机器人滑移转向的轨迹，发现机器人铅垂壁面上滑移转向，当车辆左右两侧车轮转速大小相等、转向相反时，其逆时针转向轨迹和顺时针转向轨迹因重力而呈不规则曲线，但关于y轴对称，且旋转一周后，分别位于出发点的右下方和左下方。最后提出了爬壁车辆铅垂壁面点到点的通用和简化路径规划方案。研究结果可为六轮磁吸附爬壁机器人车辆点到点的路径规划和轮速控制提供理论依据。

此模型可推广应用于四轮爬壁机器人或履带式爬壁机器人，即无限多轮式爬壁机器人。

[1] 衣正尧，弓永军，王祖温，等.用于搭载船舶除锈清洗器的大型爬壁机器人[J].机器人，2010，32(4):560－567.

[2] 衣正尧，弓永军，王祖温，等.新型船舶壁面除锈爬壁机器人动力学建模与分析[J].机械工程学报，2010，46(15):23－30.

[3] 钱志源，付庄，赵言正.一种在驱动轮打滑情况下爬壁机器人动力学建模方法[J].上海交通大学学报，2007，41(6):857－860.

[4] 李志海，付宜利，王树国.四轮驱动滑动吸盘爬壁机器人的动力学研究[J].机器人，2010，32(5):601－607.

[5] 田兰图.油罐检测爬壁机器人技术及系统研究[D].北京:清华大学，2004.

[6] 张俊强.轮履式机器人的运动分析及初始焊位的自寻优控制[D].南昌 :南昌大学，2006.

[7] 杨闫景.可壁面过渡磁吸附爬壁机器人虚拟样机设计与滑移转向模型分析[D].南京:东南大学，2013.