凹凸变化截面超高层建筑围护结构风荷载研究

肖 锟

(同济大学土木工程防灾国家重点实验室，上海 200092)

0 引言

风荷载是超高层建筑结构设计的控制性荷载，风灾给人类的灾害甚至大于地震荷载。风力与建筑外形直接相关:平面为圆形，则对抗风有利;平面凹凸多变，则对抗风不利。另外，风力受建筑周围环境影响较大，高层群中的高层抗风更为不利［2］。为了美观或功能要求，有时建筑师会考虑在超高层建筑的立面上设置凹槽或者做一些其他的不规则立面设计。这种情况将使得建筑表面的风压分布十分复杂，风荷载无法用规范［4］的方法给出，需要通过风洞试验确定。

本文是基于两栋高达300 m的超高层建筑的实际工程(如图1所示，下文分别称“北塔楼”和“南塔楼”)。该建筑周边高层建筑密集，且两塔楼间相距很近，气动干扰效应可能很强，对流场的影响将非常复杂。通过对该工程的刚性模型进行风洞试验［3］，分析了凹凸变化截面及邻近的姊妹塔楼对超高层建筑立面上最不利风压系数的影响，为复杂体型超高层建筑的围护结构风荷载设计提供参考。

1 风洞试验方法及数据处理

该项目的风洞试验是在同济大学土木工程防灾国家重点实验室的TJ-2大气边界层风洞中进行的，刚性试验模型见图2。模型的几何缩尺比为1/400。由于建筑所在的位置属于C类地貌，故本次试验在风洞中模拟了C类地貌风场，其平均风速剖面、紊流度剖面和脉动风功率谱如图3所示。同时试验还模拟了周围1 200 m直径范围内的主要建筑，以考虑风荷载干扰效应。试验时将测试模型放置在转盘中心，通过旋转转盘模拟不同风向。

图1 建筑效果图

图2 试验模型图

该项目的刚性测压模型上布置了1 392个测点，试验前经仔细检查，上述测点全部有效。南塔楼沿立面方向的部分测点的位置如图4所示。

定义来流风从正对目标建筑北立面方向吹向本工程项目时风向角为0°，风向角按顺时针方向增加。试验风向角间隔取为15°，共有24个角度。本次风洞试验的方位及风向角定义如图5所示。

试验参考点选在高度为1．237 m处，该高度在缩尺比为1/400的情况下对应于实际高度495 m。风洞测压试验的参考点风速为 10．23 m/s。

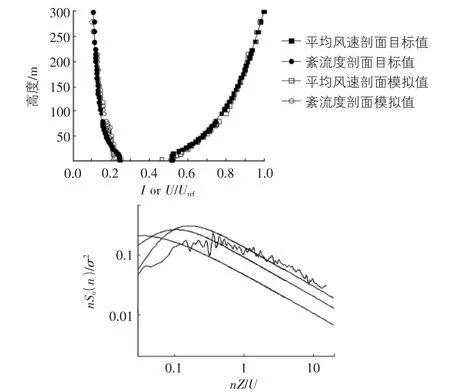
图3 风洞中模拟的C类地貌平均风速剖面、紊流度剖面和脉动风功率谱

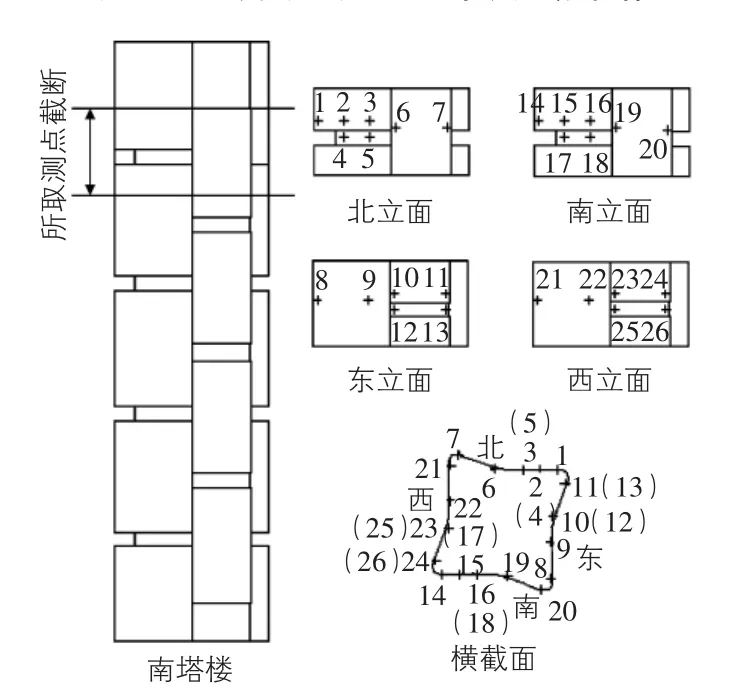
图4 南塔楼测点位置示意图

图5 项目方位及风向角定义

风压符号的约定为:压力作用向测量表面(压力)为正，而作用离测量表面(吸力)为负。

2 试验结果分析

本文给出的风压系数为体型系数，以测点高度处的来流风压为参考风压，计算式如下:

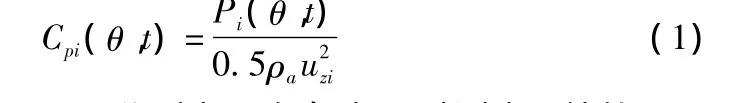
其中，Pi(θ，t)，Cpi(θ，t)分别为风向角为 θ时测点 i处的风压及风压系数时程;ρa为空气密度，这里取1．25 kg/m3;uzi为测点高度处的来流风速。

根据概率统计理论可知，各测点在某一风向来流的作用下，其风压系数的极大值CPmax和极小值CPmin可表示为:

其中，k 为峰值因子，取值范围 2．5 ～4，在这里取 k=3．5［1］。

对于每个测点，在所有风向角对应的CPmax和CPmin中，总可以找到一个最大的CPmax和一个最小的CPmin，分别称为该测点的最不利正风压系数和最不利负风压系数。得到各测点的最不利正(负)风压系数后，乘以梯度风高度参考风压，即得到了各测点的最不利正(负)风压。我国荷载规范［4］规定了，围护结构设计的风压值应按下述公式计算:

其中，μsi为测点i处的风荷载点体型系数;μzi为测点i处的风压高度变化系数;βgz为阵风系数;w0为基本风压。

由此可得到各测点在各个风向角下用于围护结构设计的风压值。对于每个测点的风压值，分别找出所有风向角中的一个最大值和一个最小值，即为该测点的最不利正风压和最不利负风压。

3 试验结果分析

3．1 最不利风压系数的分布

所选断面上各测点的最不利正风压系数见图6。各个测点的最不利正风压系数的差别较小，在1．1～1．34之间变化，平均值为1．23，这表明，建筑表面的凹凸变化对最不利正风压系数基本没有影响。图7给出了各测点上的最不利负风压系数。可以看出，不同测点上的最不利负风压系数差别很大，在-0．89～-3之间变化，均值为-1．6。这表明，建筑表面的凹凸变化对最不利负风压系数有较大影响。

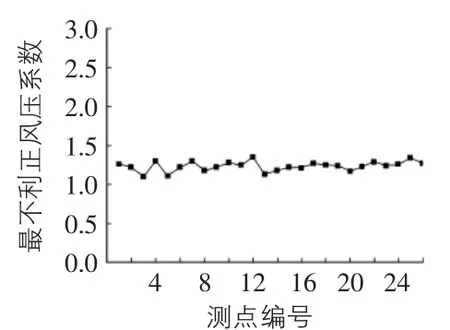
图6 各测点的最不利正风压系数

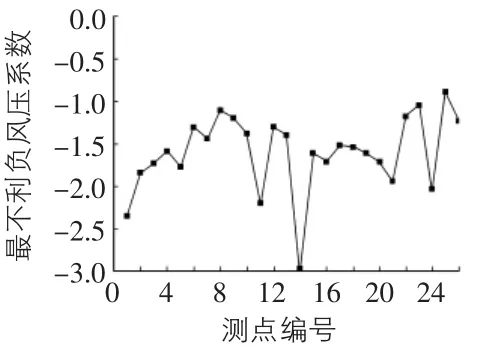
图7 各测点的最不利负风压系数

由图7还可以看出，测点C1，C11，C14，C21和C24的最不利负风压系数较大，都在-1．9～ -3之间;而测点C9，C22，C23和C25的最不利负风压系数相对较小，都在-0．8～-1．2之间。从图4中我们可以看出，测点C1，C11，C14，C21和C24正好全部落在凸角，而测点C9，C22，C23和C25都落在图5中的凹角。这表明，凸角的最不利负风压相对较大，而凹角的相对较小。测点C4，C7和C18上位于以上两类测点之间，最不利负风压系数都在-1．5 ～ -1．6 之间。

从立面上看，建筑立面凹槽处的风压系数相比于一般立面会有所不同。结合图4，从表1可以看出，位于立面凹槽处测点(测点C12，C17，C25)的最不利正风压系数相比于一般立面处测点(测点C10，C15，C23)要大;而立面凹槽处测点的最不利负风压系数与一般立面处测点相比则偏小。

表1 所选测点的最不利正负风压系数

3．2 风压系数随风向角的变化

选取凹角部位三个测点C9，C10，C22和凸角部位三个测点C11，C21，C24进行分析，得到各测点的平均风压系数和最大最小风压系数随着风向角的变化情况，如图8所示。由图8可知，测点C9，C22，C25 的风压系数分别在 -1．2 ～ +1．2，-1．4 ～ +1．3，-1．2 ～ +1．3 之间变化;而测点C11，C21，C24 的风压系数分别在-2．2～ +1．25，-1．9 ～ +1．2，-2 ～ +1．3 之间变化，变化范围相对较大。

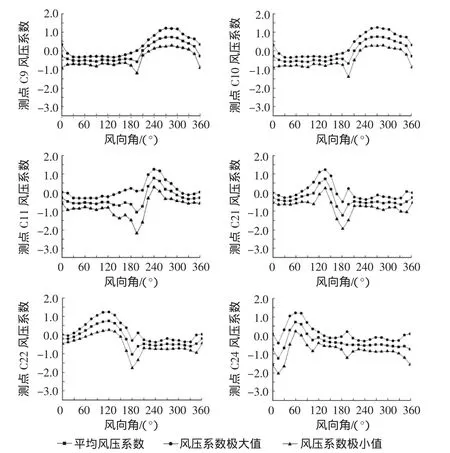
图8 测点平均风压系数及最大最小风压系数随风向角的变化（一）

位于凹角的测点 C9，C10，C22 分别在风向为 270°，270°，105°时出现最不利正压，位于凸角的测点C11，C21，C24分别在风向为240°，135°，60°时出现最不利正压。这表明，迎风时凹、凸角处均出现最不利正风压。测点C9，C10，C22分别在风向为195°，195°，80°时出现最不利负压，测点 C11，C21，C24分别在风向为 195°，180°，15°时出现最不利负压。这表明，切平面与风向平行时，凹、凸角出现最不利负风压。北塔楼和南塔楼相距十分的近，楼体在风力作用下，相互干扰是明显的，并且由于建筑外型的不规则使得建筑表面的风力作用更为突出。尤其是在两建筑物的狭缝区，狭缝效应的影响有时甚至是很危险的。试验结果分析表明，当风进入狭缝区，将对狭缝内各面的点产生明显作用，并具有一定的规律性。结合图4，图5，从图9可以看出，当风向垂直夹缝时，由于此时夹缝内的吸力很小，夹缝内立面出现最不利正压;当时风向与夹缝方向平行时，风通过夹缝时，会发生复杂的绕流，此时，风对夹缝内的点吸力作用很大，夹缝内立面出现最不利负压。

4 与规范结果对比

从图10，图11可以看出，按试验统计方法计算得到的最不利正压比规范结果小，而按试验统计方法所得的最不利负压则比规范结果大。因此，实际工程中应综合考虑按建筑结构荷载规范计算结果和应用统计理论计算结果，取最不利荷载作为最终结果。

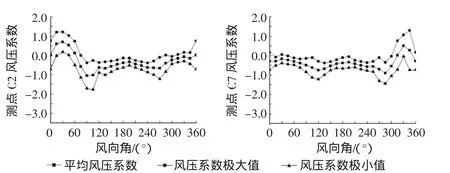
图9 测点平均风压系数及最大最小风压系数随风向角的变化（二）

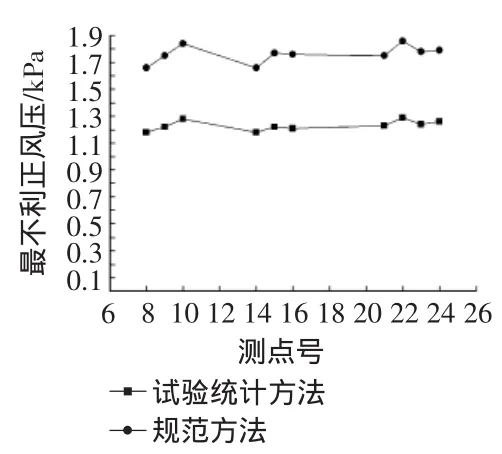
图10 测点按试验统计方法和规范方法计算得到的最不利正风压

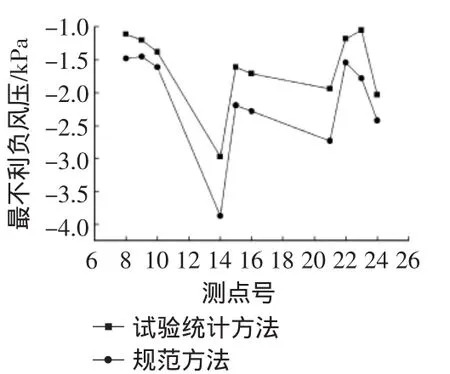
图11 测点按试验统计方法和规范方法计算得到的最不利负风压

5 结语

通过对目标建筑模型的风洞测压试验及分析，得到如下结论:

1)建筑表面的凹凸变化对最不利正压系数基本没有影响，而对最不利负风压系数影响较大;凸角处的最不利负风压相对较大，而凹角处的相对较小。2)立面凹槽处的最不利正风压系数相比于一般立面处要大;而最不利负风压系数则比一般立面处偏小。3)迎风时凹、凸角处均出现最不利正风压，切平面与风向平行时凹、凸角上的测点出现最不利负风压。4)同时两塔楼之间的气动干扰效应对夹缝内立面的最不利风压分布的影响很显著;风向垂直夹缝时夹缝内立面出现最不利正压，风向与夹缝方向平行时，夹缝内立面出现最不利负压。5)按试验统计方法计算得到的最不利正压比规范结果小，而按试验统计方法所得的最不利负压则比规范结果大。

［1］Davenport A G．Gust loading facto rs［J］．J．Struct．D iv．，ASCE，1967，93(ST3):11-34．

［2］楚 劲，刘 博，毕继红．天津市鸿吉商贸中心高层建筑群风洞试验研究［J］．建筑科学，2000(8):95-96．

［3］全 涌．郑州绿地中央广场超高层建筑风荷载研究报告［R］．上海:同济大学土木工程防灾国家重点实验室，2011．

［4］GB 50009-2001，建筑结构荷载规范(2006修订版)［S］．