圆钢管混凝土框架结构节点填充混凝土性能分析★

2013-11-06宋彬彬

山西建筑 2013年2期

宋彬彬

(湖南理工学院，湖南岳阳 414006)

0 引言

在组合结构类型中，圆柱钢管混凝土结构应用越来越广泛，由于其充分利用了钢材抗拉强度与混凝土材料的抗压强度，使两种材料在抵抗荷载与作用过程中充分发挥出其材料特性，且圆柱使内填混凝土处于三向受压而具备较高的承载能力。在圆柱钢管混凝土结构中，节点处的受力及变形均较为复杂，若能对节点的性能深入研究则有助于更好地掌握圆柱钢管混凝土结构的力学性能。本文通过分析四个圆柱钢管混凝土结构梁柱节点局部模型的试验结果，得到了圆柱内填充混凝土的应变分布规律以及构件破坏特征，此外还采用有限元数值分析方法进一步分析圆柱钢管内填充混凝土的应变分布规律，对数值分析结果与试验分析结果进行比较。

1 节点的简化

试验研究对象采用两种模型，分别考虑无横隔板加强及有贯通横隔板加强两种情况，加载方式分为单向及双向两种。其中UMN表示单向加载无横隔板节点，BMN表示双向加载无横隔板节点，而UMD表示单向加载有贯通横隔板加强节点，BMD表示双向加载有贯通横隔板加强节点。由于填充混凝土本身的材料性能使之在钢梁翼缘受压端可承担较大压力，因此，分析对象只取受拉翼缘部分可行且能够使分析过程得到简化。设定不同构件尺寸作为多个节点局部模型且施加荷载，荷载类型采用单向加载及双向加载两种方式，在两种荷载作用下，可观察填充混凝土的应变分布及破坏规律，从而考察节点混凝土的破坏特征。

2 加载及测定方法

单向荷载作用在梁翼缘端部位置且为拉力;双向荷载则一边在梁翼缘处施加拉力，一边在垂直方向的另一端梁翼缘处施加压力，并且拉伸及压缩荷载均按比例进行增减，同时保证在整个加载过程中互相垂直的两个方向上荷载绝对大小值相同。双向荷载作用导致构件开始发生破坏时，拉力维持不变，继续施加压力直到构件达到其极限承载力而产生最终破坏。在各个试件的柱填充混凝土内相应位置处放置应变片即可测量出填充混凝土的应变值，本文用C1来表示在柱钢管管壁处且与拉力方向垂直的位置，用C2来表示位于柱截面中心处且沿拉力方向的位置，通过C1及C2处测得的应变数据即可了解该处的混凝土力学性能。

3 填充混凝土的应变分布

以通过应变片测出的混凝土应变值大小为横坐标，试验施加的相应荷载值大小为纵坐标绘制出圆柱内填充混凝土的相应曲线，如图1，图2所示。

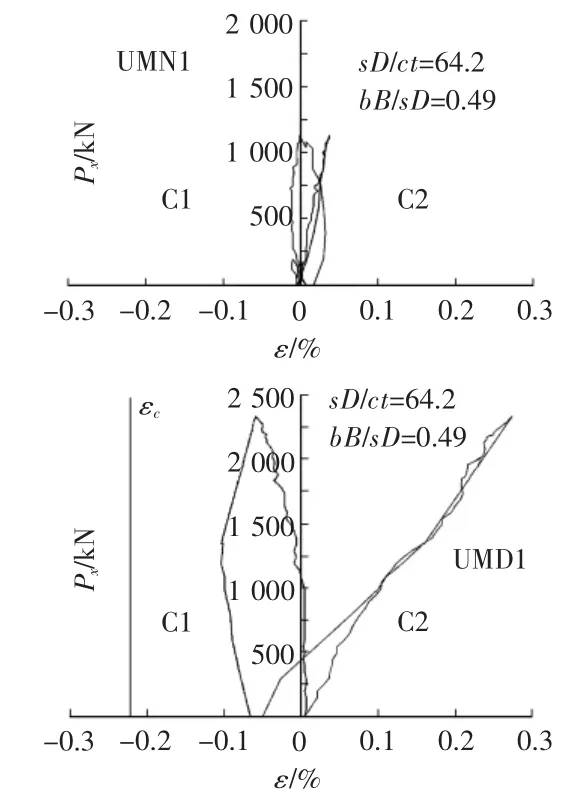
图1 单向受力试件的混凝土荷载—应变试验结果

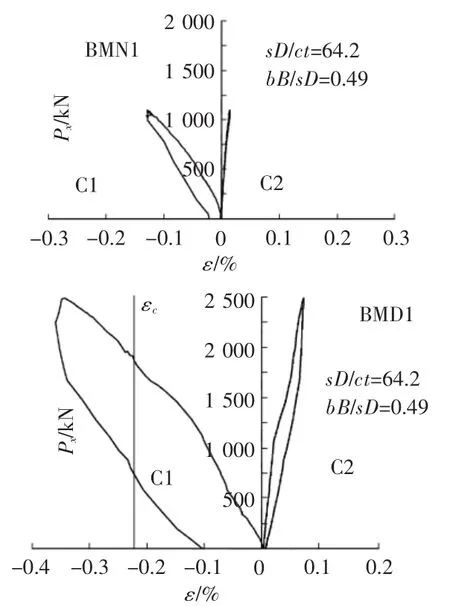
图2 双向受力试件的混凝土荷载—应变试验结果

由图1可见，在单向拉力作用下，无横隔板加强试件UMN1及有贯通横隔板加强试件UMD1在C1(柱钢管管壁处且与拉力垂直方向)处受压，在C2(柱截面中心处且沿拉力方向)处受拉。其中UMN1的拉应变及压应变均小于0.1%且压应变相差程度较大，表明受拉、受压混凝土均未达到其极限应变值。而对于采用贯通横隔板加强的试件UMD1，其在C2处的拉应变值已经接近0.3%，超过了基于混凝土材料拉压试验所得的最大值0.22%，其在C1处的压应变值也远较UMN1大，已经接近0.1%，但受拉应变及受压应变都尚未达到混凝土的极限应变值。节点处混凝土没有明显破坏，仍可看作处于弹性阶段，节点发生破坏主要体现在裂缝沿着焊缝处发展。

由图2可见，在双向荷载作用下，无横隔板加强试件BMN1及有贯通横隔板加强试件BMD1在C1(柱钢管管壁处且与拉力垂直方向)处仍受压，在C2(柱截面中心处且沿拉力方向)处仍受拉。双向试件拉应变值小于单向试件拉应变值且拉应变大小并非随拉力增大而增大，而是与钢管外径与壁厚的比值大小有关，钢管径厚比越小则拉应变越大，观察多个试件发现钢管径厚比接近25的试件其拉应变可超过0.5%。BMD1与BMN1在加载卸载过程中的压应变变化曲线形状较为相似，且双向试件的压应变值均大于单向试件的压应变值。BMD1的压应变值接近0.4%，已超过混凝土的极限压应变，但混凝土没有发生破坏。部分双向试件是由于梁先屈服而造成节点破坏。

4 试件的破坏特征

无横隔板加强的试件UMN1及BMN1最终破坏并非由于混凝土达到其极限承载力，而是由于裂缝首先在梁翼缘与柱钢管焊接处产生且沿着柱钢管的轴向逐渐扩展，造成钢管抗拉承载力不足从而使得节点丧失其承载能力。并且钢管由于受力而向外凸起，平面外变形总体呈现出椭圆形形状。而有贯通横隔板加强的试件UMD1及BMD1最终破坏则主要是由于梁翼缘与横隔板连接处的局部破坏造成的，裂缝首先在梁翼缘与横隔板连接处产生，逐渐沿横隔板向柱钢管中心发展，从而造成柱钢管管壁受拉且向外凸出，同样表现出椭圆形平面外变形形状。取出试件中的填充混凝土，可观察到在受拉翼缘侧的柱填充混凝土上留下了较为明显的椭圆形的痕迹，在受压翼缘侧的柱填充混凝土上同样也可观察到比较明显的椭圆形痕迹，从而进一步佐证了柱钢管的平面外变形。通过观察发现，填充混凝土并未出现开裂情况，这与试验分析的填充混凝土应变分布规律一致。

5 有限元分析

5.1 单元类型及材料

根据对称及简化原则，取试件的1/8进行计算且在边界处依据对称面条件施加约束，按比例相应施加荷载。将柱钢管、梁翼缘及填充混凝土均看作八节点弹塑性实体计算单元Solid45可以较好地模拟实际情况，分析中不可忽略焊缝的影响，因此对焊缝也设为Solid45;在受荷过程中，柱内填充混凝土与柱钢管管壁之间会产生脱离，用三维面—面接触单元Conta174和Targe170来考虑这一情况;忽略填充混凝土与钢管间的粘结与摩擦。梁翼缘和柱管壁采用的钢材其应力—应变关系为多线性模型且钢材以及焊缝的材料屈服准则采用Von Mises准则;柱内的填充混凝土其应力—应变关系为双线性模型，屈服准则则采用Drucker-Prager屈服准则。

5.2 有限元结果及分析

通过有限元分析同样可得到填充混凝土的荷载—应变关系，以混凝土应变值大小为横坐标，施加的相应荷载值大小为纵坐标绘制出圆柱内填充混凝土的相应曲线，如图3，图4所示。观察可知，所有试件在C1(柱钢管管壁附近且与拉伸荷载垂直方向)处受压，在C2(钢管中心处且沿受拉梁翼缘轴向方向)处受拉。单向试件UMN1的应变图形与试验结果较为接近，拉压应变值均比较小;UMD1的拉应变值接近于0.25%，与试验结果较为类似，但压应变值较小，与试验结果相比绝对值大小偏低，造成结果有微小误差的原因可能是材料参数的选取不够准确以及在数值分析时接触分析与实际情况有误差。

图3 单向受力试件的混凝土荷载—应变有限元结果

图4 双向受力试件的混凝土荷载—应变有限元结果

双向试件的应变图形形状与试验结果较为接近，且拉应变数值都比较小，均未超过0.1%，但压应变值均比较大。BMN1的压应变已经接近0.2%，而BMD1的压应变值则已达到0.22%，但与试验结果相比偏小。数值分析结果表现出对双向试件而言，是否设置贯通横隔板对柱钢管的内填混凝土应变影响并不大。对图1～图4进行综合比较分析可知，数值分析结果与试验结果相比误差不大，可见采用有限元分析来模拟试验是可行的。