太阳帆悬浮轨道的动力学特性分析
2013-11-04陈翠红和兴锁宋明
陈翠红, 和兴锁, 宋明
(西北工业大学 工程力学系, 陕西 西安 710129)
2012-06-04;
2012-09-17; < class="emphasis_bold">网络出版时间
时间:2012-12-11 12:16
国家自然科学基金资助(10672133)
陈翠红(1985-),女,湖北云梦人,硕士研究生,研究方向为航天器动力学与控制。
太阳帆悬浮轨道的动力学特性分析
陈翠红, 和兴锁, 宋明
(西北工业大学 工程力学系, 陕西 西安 710129)
研究了太阳帆悬浮轨道的动力学特性,主要分析了稳定性条件。首先建立垂直于太阳-行星连线的悬浮轨道模型,在柱坐标系下,依据Hamilton原理得到悬浮轨道角动量与太阳光压的关系。然后,针对小扰动情况运动方程,分析悬浮轨道线性与非线性稳定性条件。最后,运用Hamilton-Jacobi理论进行变量分离,得到物理意义明显的动力学方程。仿真结果表明,选取合适的初始值,可以实现稳定的太阳帆悬浮轨道。
太阳帆; 悬浮轨道; 稳定性; Hamilton原理
0 引言
太阳帆本质上是连续小推力推进方式,可形成许多独特的非开普勒轨道, 如日心悬浮轨道、行星悬浮轨道、人工拉格朗日点轨道等[1]。NASA,ESA等航天机构早在20世纪70年代就开始进行相关研究,但限于几项关键技术未突破,大型太阳帆飞行任务尚未得以成功实施。随着太阳帆技术的快速发展,人们更多地关注小型太阳帆[2]。小型太阳帆与大型太阳帆本质上无区别,但更易工程实现。日美两国已在2010年先后成功实施各自的小型太阳帆空间飞行试验。
在太阳帆悬浮轨道稳定性领域,文献[3-5]对日心悬浮轨道、行星悬浮轨道和拉格朗日点上的太阳帆编队稳定性进行了研究,取得了较好的结果。基于以上研究,本文采用Hamilton动力学方程和Hamilton-Jacobi理论对太阳帆悬浮轨道的稳定性进行了分析。
1 垂直太阳-行星连线的行星悬浮轨道
太阳帆位于非开普勒轨道,忽略地球引力位函数高阶项和其他星体引力摄动。悬浮轨道垂直于太阳-行星连线,太阳光压力假设为常量,行星悬浮轨道如图1所示。
使用归一化单位(太阳帆的质量为单位质量m,地球绕太阳的公转角速度为单位角速度ω,地球到太阳的距离为单位长度L),太阳帆的轨道动力学方程在惯性坐标系下用柱坐标(ρ,θ,z)可表示为[6]:
(1)
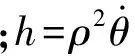
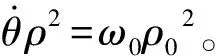
h=ωρ2=ω0ρ02
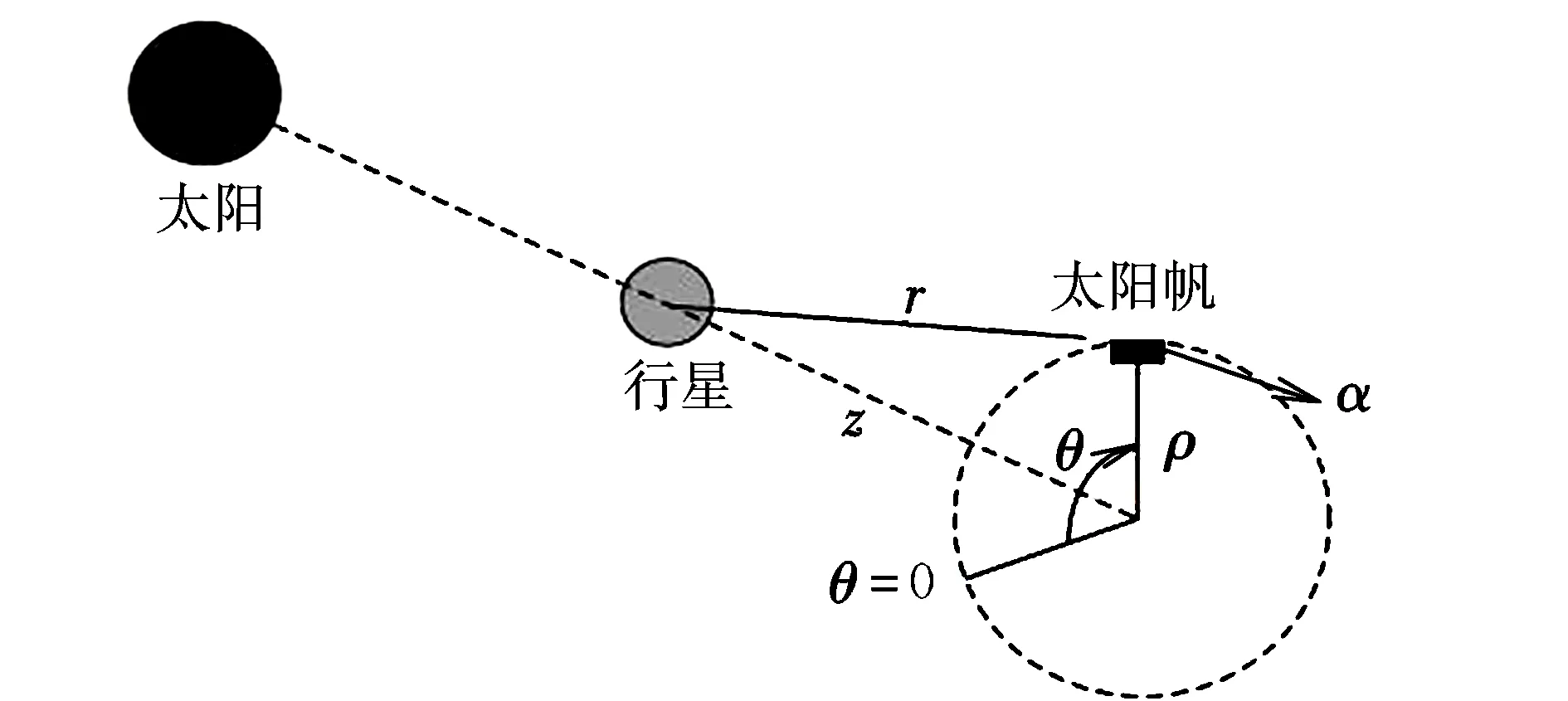
图1 行星悬浮轨道示意图
2 Hamilton运动方程
太阳帆的在轨运行,除大气耗散因素影响外,对应的是Hamilton系统,还可以用Hamilton力学中的变换方法来建立相应运动方程。观察式(1),动力学方程可以表示为:
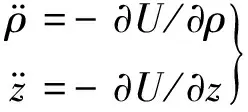
(2)
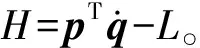
根据Hamilton正则运动方程:
1+ρ6κ2/h4=(1/3)κρ2
(3)
由式(3)求得:
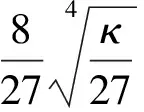
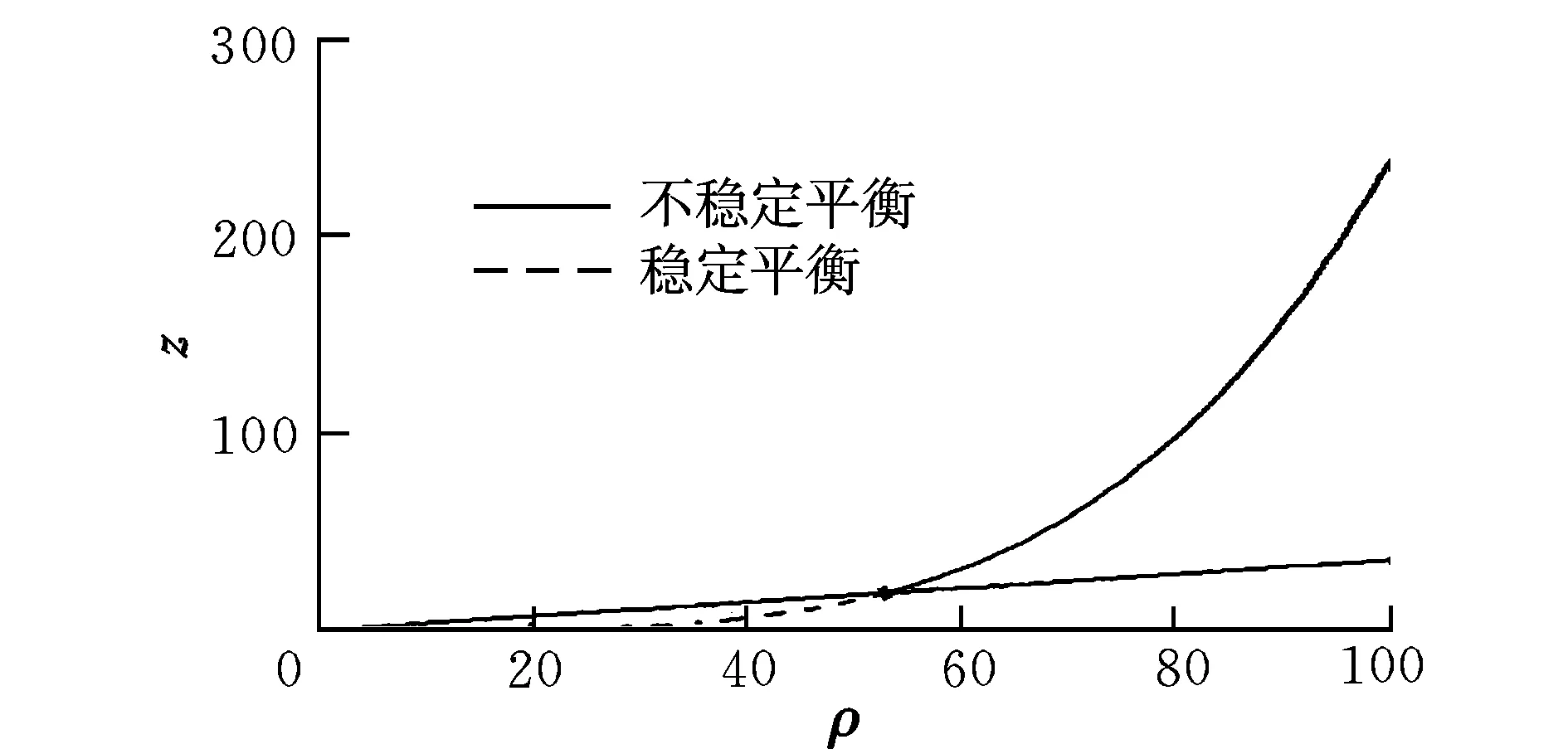
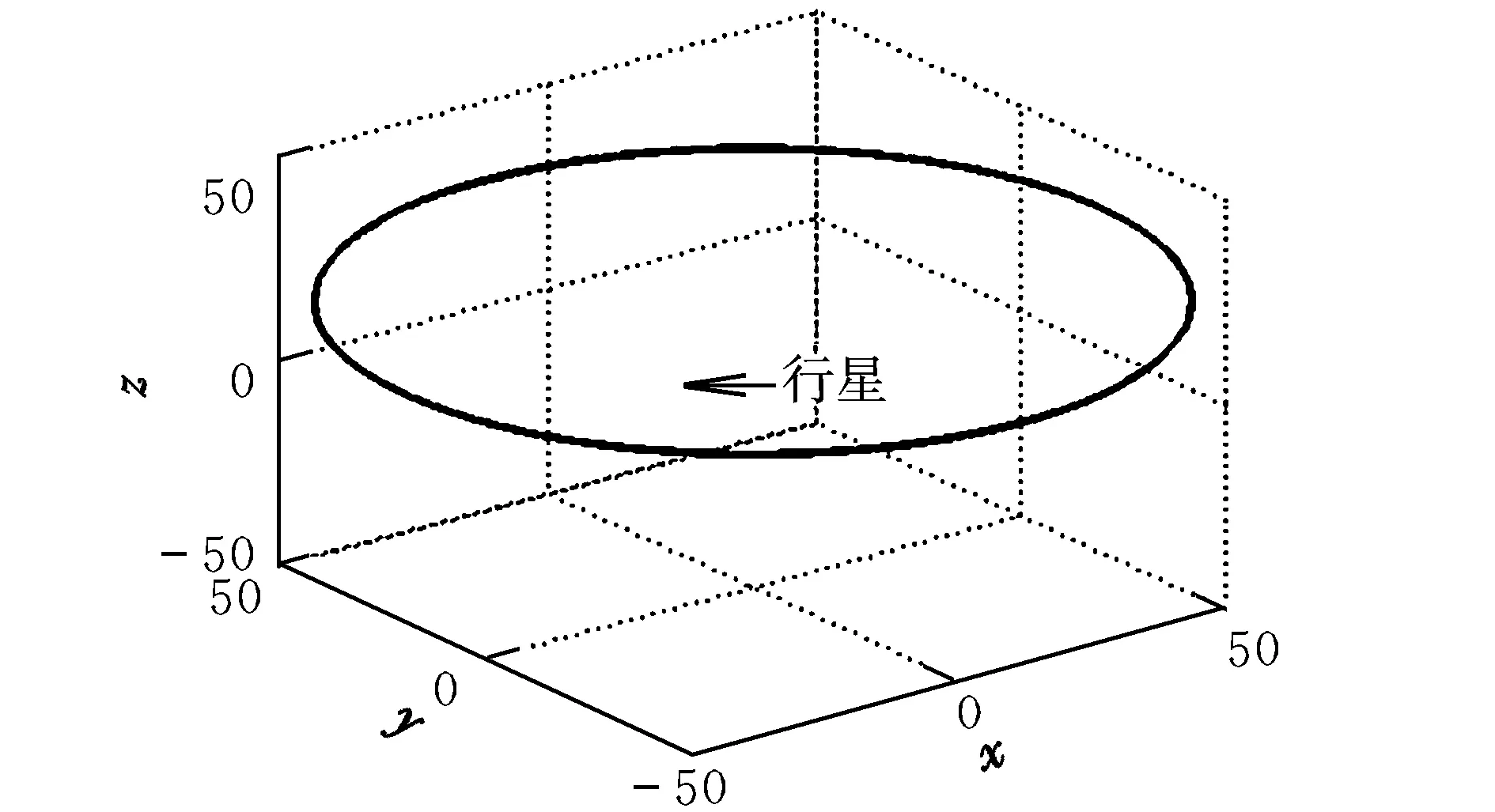
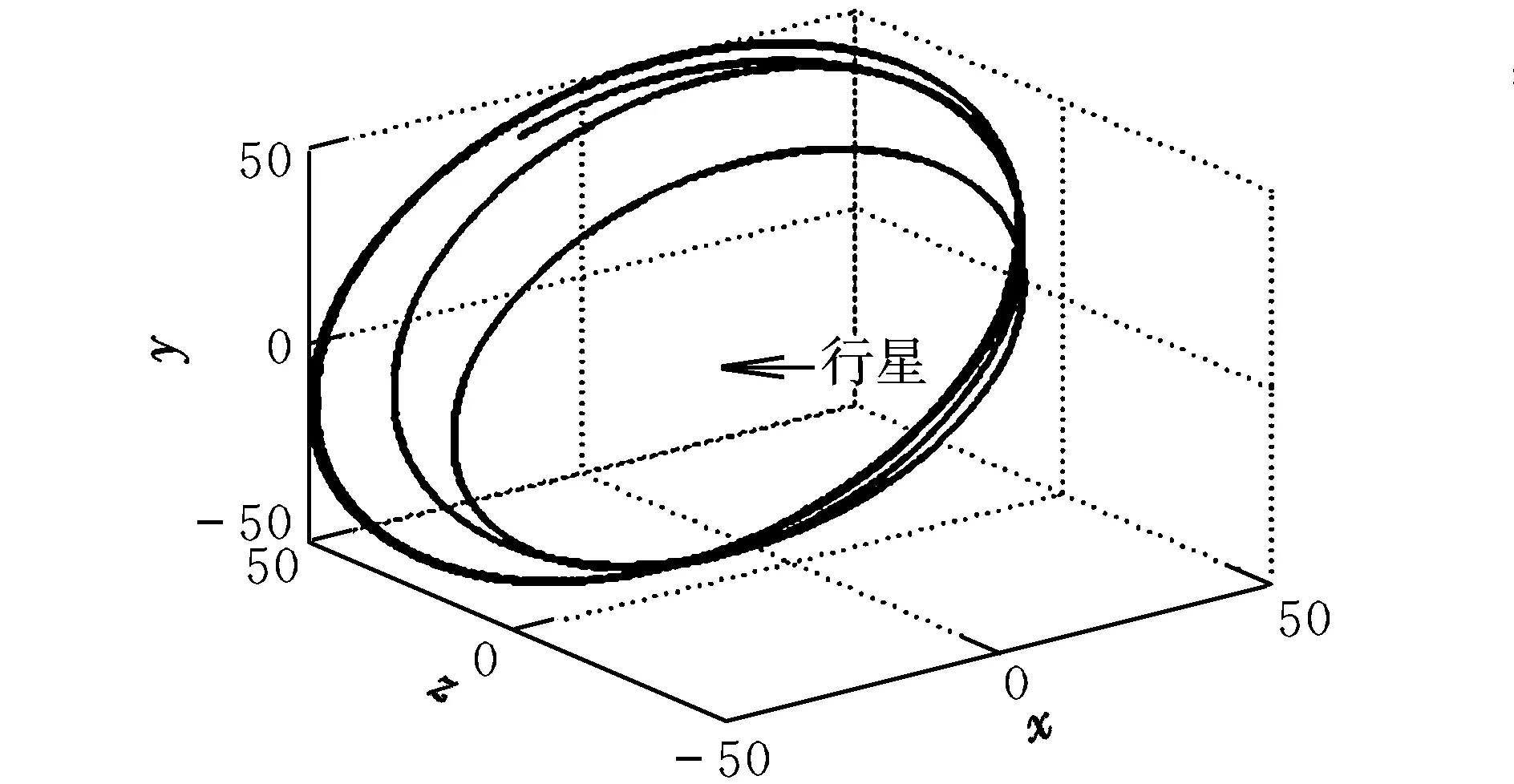
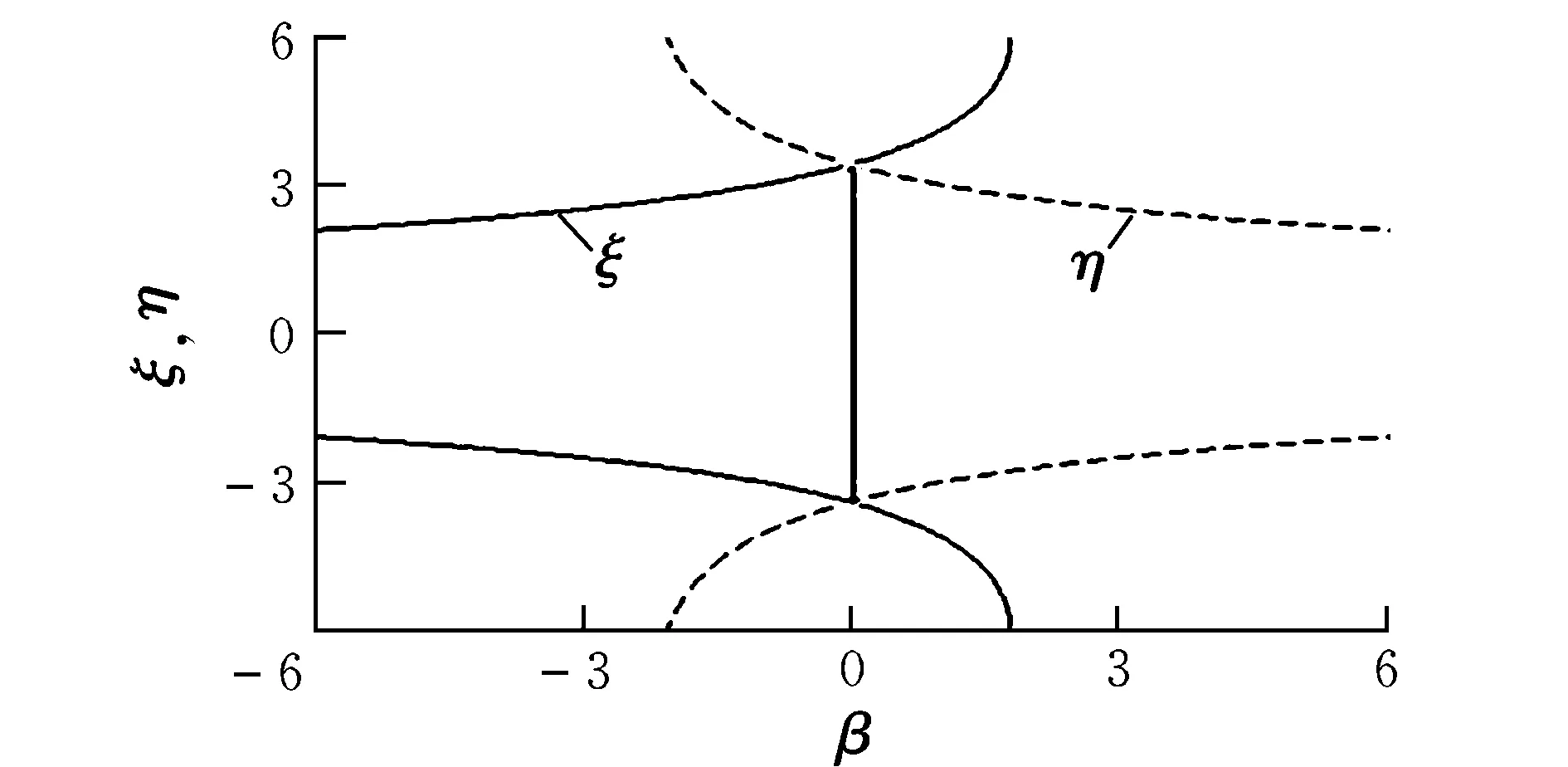
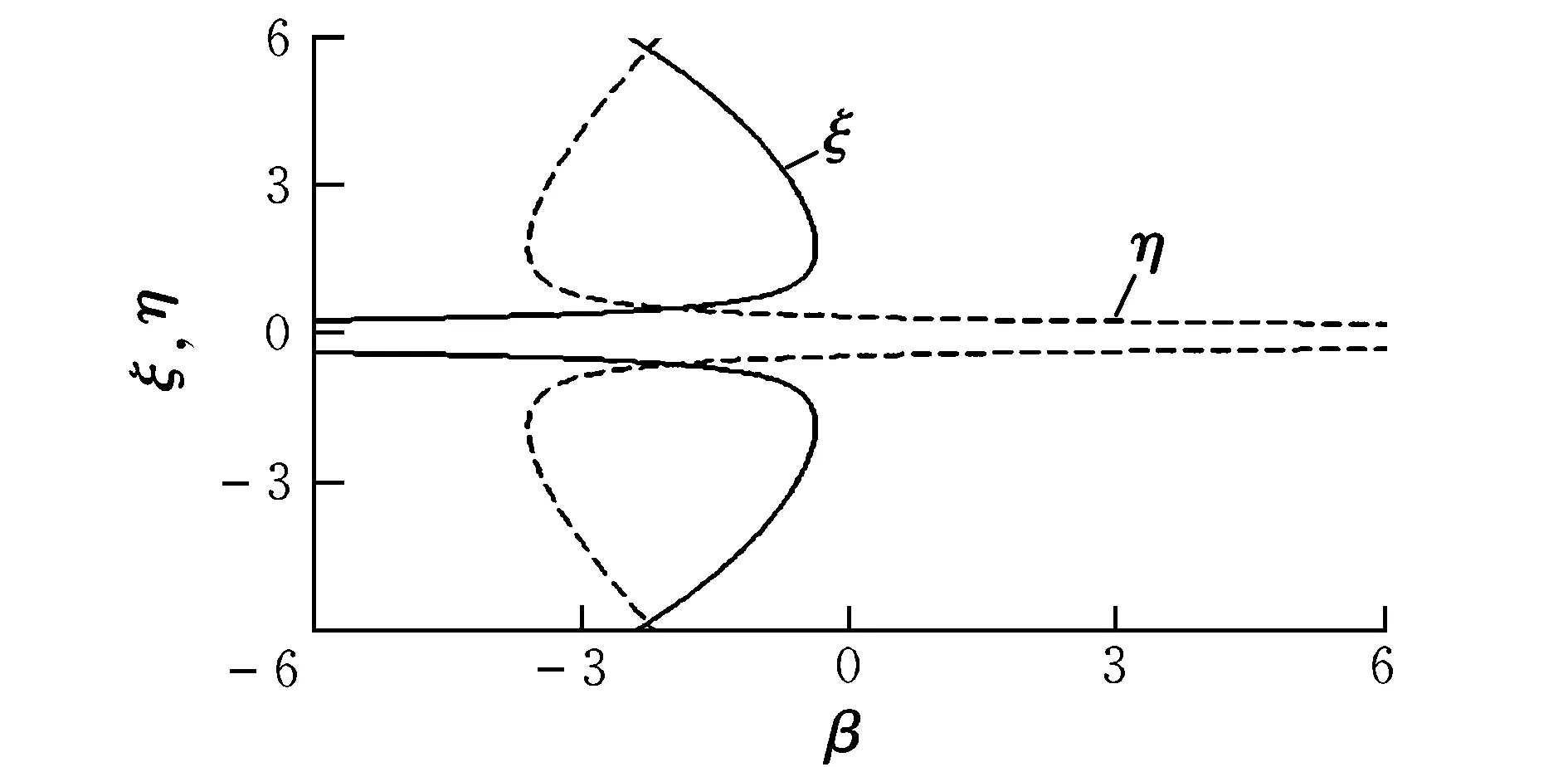
当h>hmax时,系统不平衡,不能产生悬浮轨道;当h 图2 平衡位置图 3.1 线性稳定条件 假设fρ=h2/ρ3-ρ/r3,fz=-z/r3+κ;增加一小扰动ρ=ρ0+δρ,z=z0+δz泰勒展开,得到线性方程为: (4) 忽略高阶项,其中A11,A12,A21,A22表示偏导∂fρ/∂ρ,∂fρ/∂z,∂fz/∂ρ,∂fz/∂z。悬浮轨道各个偏导数分别为: (5) 扰动用向量δQ表示,δQ=[δρ,δz]T,方程(4)的矩阵形式为: (6) 常系数方程可以假设|δQ|=Q0exp(λt),λ为常系数。带入方程(6),特征多项式为: (7) 图3 线性稳定悬浮轨道 图4 线性不稳定悬浮轨道 3.2 非线性稳定条件 U(ρ,z)=h2/2ρ2-1/r-κz (8) 若定义Uρρ,Uzz,Uρz分别为对函数U(ρ,z)的二阶偏导和二阶混合偏导,则当Uρρ>0,Uzz>0,UρρUzz-Uρz>0时,势能函数的局部极小值对应稳定的悬浮轨道。 (9) 非线性稳定和不稳定悬浮轨道如图5和图6所示。 图5 非线性稳定悬浮轨道 图6 非线性不稳定悬浮轨道 2/(ξ2+η2)-κ(ξ2-η2)/2 (10) 其中: Hamilton主函数设为S(ξ,η,t)=-Et+pθθ+S(ξ)+S(η)。写Hamilton-Jacobi方程为: (11) 分离变量,则有: (12) β为任意常数[8]。于是,给定一系列的初始值,E,pθ,β可以计算,令pξ,pη为零,解方程(12),得到ξ,η的值。 (13) 图7和图8为稳定和不稳定轨道区域图。 图7 稳定轨道区域图 图8 不稳定轨道区域图 运用Hamilton-Jacobi理论分析太阳帆悬浮轨道的轨道系数,在抛物线坐标系下,β约为0.225时轨道系数ξ,η可以趋近于零(此时κ=1.054 5×10-4);轨道系数ξ,η在β为另一数值时是发散的(此时κ=2.348 0×10-4),趋于无穷。 本文研究太阳帆的动力学特性,通过重点分析垂直于太阳行星连线的行星悬浮轨道,利用Hamilton方程和Hamilton-Jacobi理论分析太阳帆悬浮轨道的稳定性,实现线性和非线性稳定性条件。由Hamilton-Jacobi理论分析得到物理意义明显的动力学方程,可以实现太阳帆行星悬浮轨道稳定,为该领域的进一步研究提供了依据。 [1] 曾志峰,汤一华,陈士橹,等.基于行为的太阳帆编队方法[J].西北工业大学学报,2012,30(1):44-49. [2] McInnes C R.Solar sailing-technology,dynamics,and mission applications[R]. United States:Springer-Praxis Publishing Ltd,1999. [3] Gong Shengping,Baoyin Hexi,Li Junfeng.Solar sail formation flying around displaced orbits[J].Journal of Guidance,Control,and Dynamics,2007,30(4):1148-1151. [4] Gong Shengping,Li Junfeng,Baoyin Hexi.Formation around planetary displaced orbit[J].Applied Mathematics and Mechanics(English Edition),2007,28(6):759-767. [5] 龚胜平.太阳帆航天器动力学与控制研究[D].北京:清华大学,2009. [6] Xu Ming, Xu Shijie. Nonlinear dynamical analysis for displaced orbits above a planet[J].Celetial Mechanics and Dynamical Astronomy,2008,102(4):327-353. [7] Bookless J,McInnes C.Dynamics and control of displaced periodic orbits using solar-sail propulsion[J].Journal of Guidance,Control,and Dynamics,2006,29(3):527-537. [8] Landau L D, Lifschitz E M. Mechanics-course of theoretical physics[R]. Oxford: Pergamon,1976. Analyzingdynamiccharacteristicsofthedisplacedorbitaboveaplanetwithsolarsail CHEN Cui-hong, HE Xing-suo, SONG Ming (Department of Engineering Mechanics, NWPU, Xi’an 710129, China) This article studies kinetic characteristic of solar sail displaced orbit and analyses stability conditions. Firstly, by establishing displaced orbit model which is normal to sun-planet and assuming solar radiation pressure as constant, the relationship between displaced orbit angular momentum and solar radiation pressure can be derived through Hamilton dynamics method. Considering small perturbations of motion equation, the stability condition of linear and nonlinear displaced orbit can be derived. Finally, using Hamilton-Jacobi theory, the kinetic equation with significance physical meaning can be derived by variable separation. Simulation results show that stable solar sail displaced orbit can be realized by choosing proper initial value. solar sail; displaced orbit; stability; Hamilton principle V412.41 A 1002-0853(2013)01-0065-04 (编辑:方春玲)
3 悬浮轨道动力学特性分析
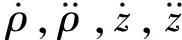
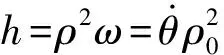
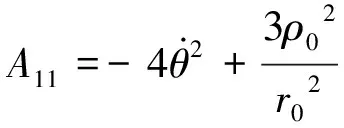
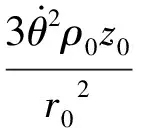
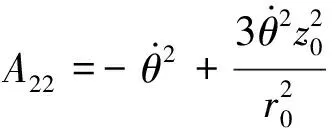
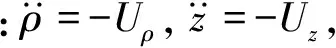
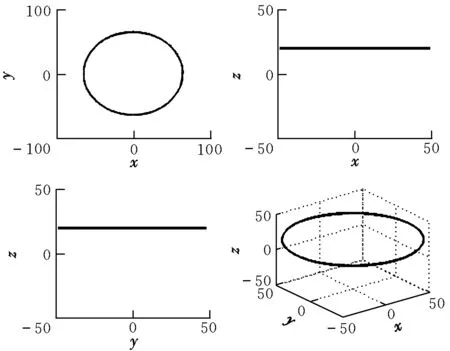
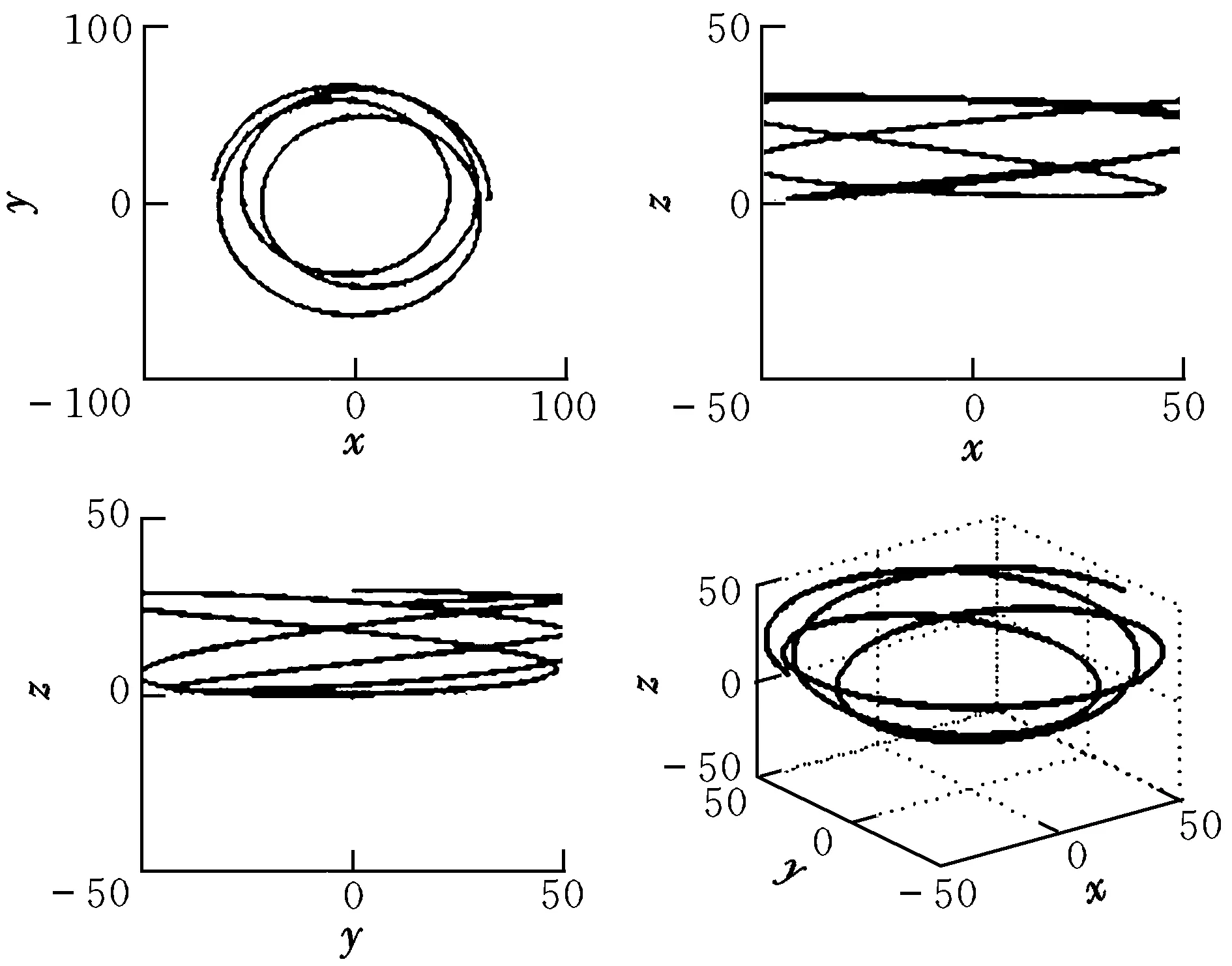
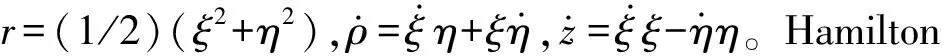
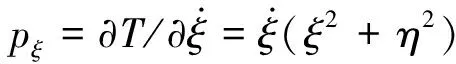
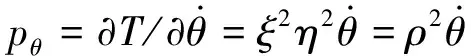
4 结束语
