基于修正边界层转捩的翼型气动特性研究

张瑞民，于金玲

(中国航天空气动力技术研究院第二研究所，北京100074)

0 引言

目前，在飞行器研制过程中，关于升力的计算精度很高，能够达到实际要求，但阻力的计算精度相对较低。尤其对大展弦比机翼和超临界机翼来说，摩擦阻力占整个阻力的主要部分，而影响摩擦阻力特性的关键因素是边界层转捩和分离。因此，准确预测边界层的转捩点位置对于提高飞行器的气动特性预测精度具有重要意义。

由于对边界层转捩的物理机理缺乏认识，能有效预测边界层转捩的理论还不成熟。目前，工程上常用的转捩预测方法主要有［1-2］:(1)eN方法［3-4］;(2)经验关系式;(3)低雷诺数模型方法。eN方法以线性稳定性理论为基础，同时与风洞试验相结合，能够预测低雷诺数下二维翼型的自然转捩和分离流转捩，却难以模拟bypass转捩，且难以推广到三维流动;经验关系式则基于大量的试验数据，借助适当的关系式可以预测自然转捩和bypass转捩等，但因该方法引入边界层动量厚度，致使其与CFD方法不相容［5］;低雷诺数湍流模型是从N-S方程推导出来的流场中脉动量的描述方程，具有模拟脉动量发展、捕捉层流到湍流流态转变的能力，不仅能够反映转捩现象，而且仅涉及当地变量，与现代CFD技术完美相容。

本文以k-ωSST两方程湍流模型为研究对象，引入间歇函数对其所带的Wilcox转捩模式进行了修正，进而对传统湍流翼型的气动特性进行了研究。

1 数值方法

1.1 控制方程

流场计算采用基于压力和速度耦合的SIMPLE算法来求解定常可压缩的N-S方程，即:

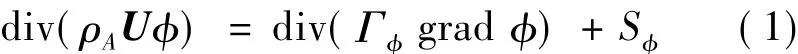
式中，ρA为气流的密度;U为气流速度矢量;Γφ为扩散系数;Sφ为源项;φ为通用项;边界条件选用压力远场和无滑移壁面边界条件;方程的离散采用有限体积法;为了保证计算求解稳定和收敛，所有求解方程的对流项采用二阶迎风格式，扩散项采用中心差分格式。

1.2 湍流模型

湍流模型选用k-ωSST两方程模型，湍流运动方程如下:

式中，ρ为空气密度;Gk，Gω为k和ω的生成项;Yk，Yω为由湍流引起的k和ω的耗散项;Γk，Γω为k和ω的有效扩散系数，即:

式中，μ为层流黏性系数;μt为湍流黏性系数，表达式为:

式中，S为应变率幅值;α1为常数;F2为混合函数。在高雷诺数下，间歇函数α*=1，此时流动为湍流，如果考虑低雷诺数转捩的影响，Wilcox的间歇函数表达式为:

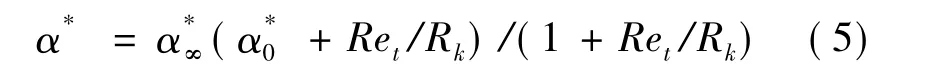
式中，α*0=0.024;Ret=ρk/(μω);Rk=6。

1.3 转捩模式修正

由于基于k-ωSST两方程湍流模型的原始Wilcox转捩模式本身对扰动过于敏感，使得边界层转捩位置比实际情况明显靠前，致使边界层流动很快从转捩区域进入到全湍流区域，进而影响了翼型的流场特性和气动性能。因此，本文从转捩流动的物理特征出发，针对湍流黏性系数中的间歇函数进行调整，使其既能模拟全湍流流动，又能模拟边界层转捩的流动特性。由于间歇函数仅仅是湍流雷诺数Ret的函数，因此只对 Ret进行修正，修正后的Ret为［6］:

2 计算结果与分析

本文分别在未考虑转捩和修正转捩模式的情况下，研究了NACA0012翼型的流场特性和气动性能。翼型周围网格以及局部放大图如图1和图2所示，壁面第一层网格满足y+≤1.0，计算域四周边界距翼型表面均为弦长的20倍。

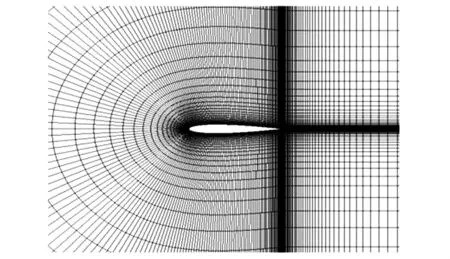
图1 NACA0012翼型的网格划分

图2 翼型网格的局部放大图

计算条件为:Ma=0.3;Re=3 × 106;ω =k/μt，湍流参数取值为 k=(0.001×U∞)2，μt=0.009μ。

图3和图4分别给出了在原始的Wilcox转捩和修正的Wilcox转捩模式下翼型的升力系数和阻力系数随迎角的变化关系，并与文献［4］中的试验值进行了比较。由图可知，与原始的Wilcox转捩模式相比，基于修正后的Wilcox转捩模式的阻力预测结果与试验值相比更接近，但仍有较大的差距。

图5给出了翼型在不同迎角下基于原始的Wilcox转捩模式和修正的Wilcox转捩模式的边界层转捩位置，并与文献［7］中的试验结果进行了比较。其中，xtr/c为翼型上表面的转捩位置与弦长之比，α为气流迎角。从图中可以看出，基于修正的转捩模式，对阻力的预测精度有了一定程度的提高。

图3 升力系数随迎角的变化关系

图4 阻力系数随迎角的变化关系

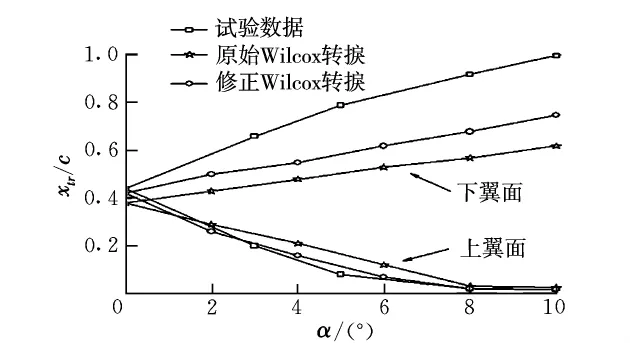
图5 不同迎角下翼型上、下表面的转捩位置

图6和图7分别给出了在0°和4°迎角下转捩模式修正前后翼型上表面压力分布的计算结果。通过比较可以看出，在不同的Wilcox转捩模式下，翼型表面的压力分布基本一致。图8和图9分别给出了在0°和4°迎角下转捩模式修正前后翼型上表面摩擦阻力分布的计算结果。与0°迎角相比，迎角为4°时的翼型上表面的顺压梯度区减小，逆压梯度区增加，导致边界层流动提前转捩，这与试验结果相符;此外通过比较可以看出，当迎角为0°和4°时，基于本文的转捩模式修正，翼型表面的转捩位置预测结果与试验值更加接近。

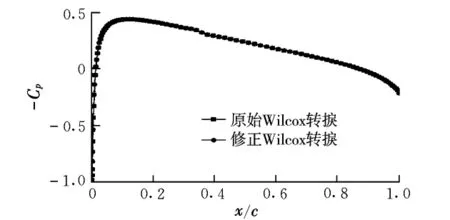
图6 翼型上表面压力系数分布(α=0°)

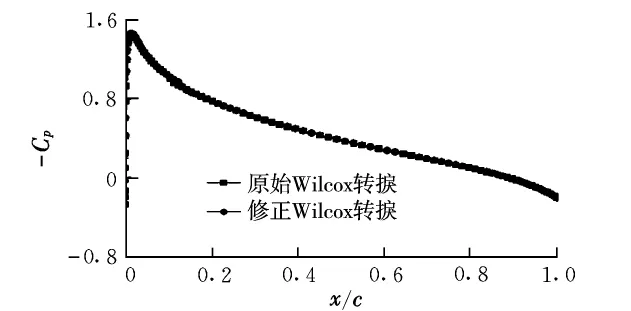
图7 翼型上表面压力系数分布(α=4°)

图8 翼型上表面摩擦系数分布(α=0°)

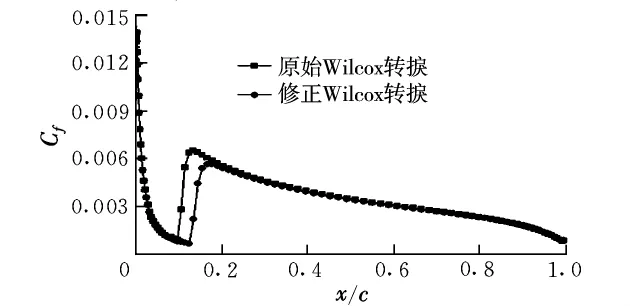
图9 翼型上表面摩擦系数分布(α=4°)

3 结束语

边界层转捩是决定翼型气动特性的重要因素。本文从转捩流动的物理特征出发，引入间歇函数对SST湍流模型的Wilcox转捩模式进行了修正，并选取了典型的有压力梯度的NACA0012翼型进行了计算和验证。研究表明，改进后的模型对转捩位置具有更好的预测能力;在采用修正边界层转捩模型的情况下，翼型的阻力预测精度有了一定程度的提高，但与试验结果相比，仍存在差距，有待进一步改进。参考文献:

［1］徐星仲．转捩流动的数值方法研究［D］．北京:中国科学院工程热物理研究所，1996．

［2］是勋刚．湍流［M］．天津:天津大学出版社，1994:136-138．

［3］Smith A M O，Gamberoni N．Transition，pressure gradient and stability theory［R］．USA:Douglas Aircraft Company，1956．

［4］Van Ingen JL．A suggested semi-empirical method for the calculation of the boundary layer transition region［R］．Delft，Holland:University of Technical Aerospace Engineering，Report VTH-74，1956．

［5］Langtry R B，Menter F R．Transition modeling for general CFD applications in aeronautics［R］．AIAA-2005-0522，2005．

［6］钱炜祺，詹浩．一种基于湍流模式的转捩预测方法［J］．空气动力学学报，2006，24(4):502-507．

［7］Johansen J，Sorensen JN．Prediction of laminar/turbulent transition in airfoil flow［R］．AIAA-98-0702，1998．