可变形翼战术导弹LPV增益调度控制

张公平, 段朝阳, 廖志忠

(中国空空导弹研究院 制导控制系统研究所, 河南 洛阳 471000)

可变形翼战术导弹LPV增益调度控制

张公平, 段朝阳, 廖志忠

(中国空空导弹研究院 制导控制系统研究所, 河南 洛阳 471000)

在导弹飞行过程中,弹翼变形会导致快变气动与多体运动耦合。为了精确描述导弹变翼飞行的时变特性,基于质点系动量及动量矩理论,建立了变翼导弹非线性多体动态模型,并通过状态变换法,将其转换为线性参变动力学模型。利用改进的D-K迭代算法,设计了轴对称变翼导弹的LPV增益调度控制器。通过非线性联合仿真,验证了LPV鲁棒控制器对组合变翼扰动具有良好的控制品质及鲁棒性,能胜任较大空域的变翼稳定与控制。

变形翼; 战术导弹; 多体动力学; 增益调度控制

0 引言

为充分发挥导弹远程威慑与灵活作战的能力,在新的战场形势下,军方对攻击机动目标导弹的射程及机动性提出了新的、更高的要求,从而促使导弹研究领域的专家们不断推陈出新。

国内外学者曾提出并开展了多项概念新颖的可变外形导弹的研究。例如,英国Cranfield大学的偏转弹头研究,证实了由弹头偏转引起的非对称布局可以大幅度提高导弹的机动性[1]。美国Raytheon公司的新概念导弹通过对称变翼展提高了“战斧”巡航导弹的最大射程[2]。2008年,Matthew等通过实验研究了一种机载斜置翼导弹的气动特性,验证了弹翼适当斜置有利于减小阻力、增加射程；实验结果还表明,机弹分离时,该斜置翼导弹在较大的机翼后掠角范围内具有良好的静稳定性[3]。2008年,Matthew将导弹的结构动力学方程与N-S方程相结合,采用重叠网格生成技术,对弹翼斜置时的气动弹性效应进行了高可靠度的数值模拟[4]。在飞行力学与控制领域,Jae-Sung Bae等的研究表明,非对称变翼展具有很强的横滚控制能力,可取代传统控制面用于横向控制[5]。近年来,有关变翼导弹的研究逐步深入,开始转向变翼飞行控制问题的解决。如Sigler等将巡航导弹的可反对称变翼展视为新型操纵面,通过拟合求导获得气动导数,并采用将滑模与反馈线性化相结合的方法设计了非线性控制器[6]。在国内,中国空空导弹研究院也开展了系统、深入的研究,为弹翼可变形的远程空空导弹设计了线性鲁棒控制器[7]。此外,西北工业大学针对变翼导弹的小扰动线化模型,分别设计了线性的PID和变结构控制器[8-9]。事实上,目前有关变翼导弹的控制器设计多是针对单刚体线性动态模型,将变翼扰动简单地建模为一个固化的不确定参数,无法细致刻画变翼扰动的可预测性及时变特性,最终导致设计出的控制器性能受限。

本文将充分考虑连续变翼对弹体动态特性的影响,采用状态变换法构造变翼飞行的准线性化模型,并通过一类扩展功能的D-K迭代算法,对准线化模型的线性分式变换形式进行鲁棒控制器设计与优化,以应对导弹高速、高机动飞行中快速变翼对飞行控制系统的复杂扰动。

1 变翼导弹线性参变动力学建模

定义弹翼固连坐标系如图1所示。

图中,Ciξi轴与翼根弦平行,指向弹头为正;Ciζi与翼平面后缘线平行,向外指向为正。此外,坐标系Oξitηitζit为弹翼质心固连系Ciξiηiζi的平移坐标系,Ci为第i号可动弹翼的质心,χ为脊线后掠角,l为弹翼质心到根弦最大厚度点S的距离,点S在弹体纵轴上的投影点为C,其距弹头尖端的距离为LC,弹体质心为Cb,距弹头尖端的距离为Lb。若Xw,Zw分别为弹翼质心在弹体系下的位置,mw为单片弹翼的

质量,根据瞬时单刚体原理,多刚体运动的任意瞬时其质心运动方程与固定翼导弹类似[10-11],则由动量矩定理可得变翼导弹的转动动态模型为:

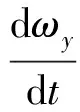
考虑到弹体及变翼的轴对称特性,通过纵向与侧向运动分离,可得变翼导弹的纵向动力学模型为:

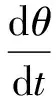
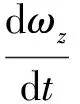
式中，Cz为附加转动惯量。

令状态变量为α和ωz,控制输入为δz,则整理可得状态方程为:

可见,变翼导弹的转动动力学模型与固定翼导弹有所不同,主要表现为弹翼运动引起的附加惯性及隐含的快变气动特性。为得到便于鲁棒控制器设计的动态模型,可采用状态变换法的基本思想将非线性系统状态沿着一条平衡轨迹进行数学变换。进一步建立变翼导弹纵向短周期运动的LPV形式:

若采用过载控制,则定义输出方程为:

事实上,只要简化得当,且控制量维数与状态变量x1的维数一致,则多变量运动模型的LPV建模就适用状态变换法。

2 变翼导弹LPV模型的LFT实现

尽管变翼导弹LPV系统的系数矩阵是时变的,但通过LFT变换,可将其不确定性明确分离出来,如下式的标准LPV形式:

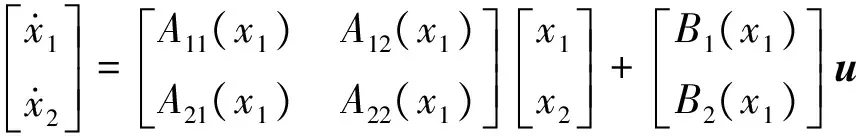
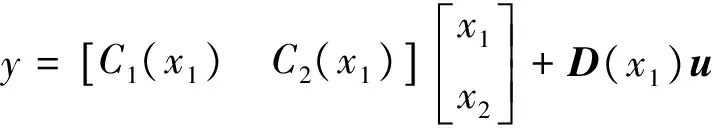
非零矩阵元素以线性分时变换的形式给出:

A22=Fu(MA,ΔA),B1=Fu(MB1,ΔB1)

B2=Fu(MB2,ΔB2),C1=Fu(MC,ΔC)

则LPV系统的LFT连接关系如图2所示。

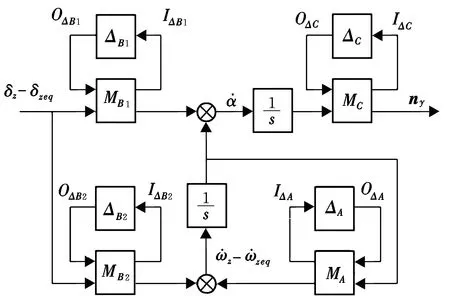
图2 导弹LPV系统的LFT结构图Fig.2 LFT structure of missile LPV system

图中,不确定块为ΔA,ΔB1,ΔB2,ΔC;确定性块为MA,MB1,MB2,MC,进一步可得标称系统的状态空间形式为:

不确定性矩阵为:

可见,变翼导弹动态模型的时变部分可以通过不确定性Δ的形式从其标称部分中分离出来,以便满足鲁棒控制器设计对动态模型形式的要求。

3变翼导弹LPV/μ综合增益调度

控制

为实现变翼过程中导弹控制系统的增益自调度,可采用控制器与不确定性直连的结构,即Fl(K,Δ)为广义控制器,可随不确定参数Δ而变化,其等效的控制结构如图3所示。

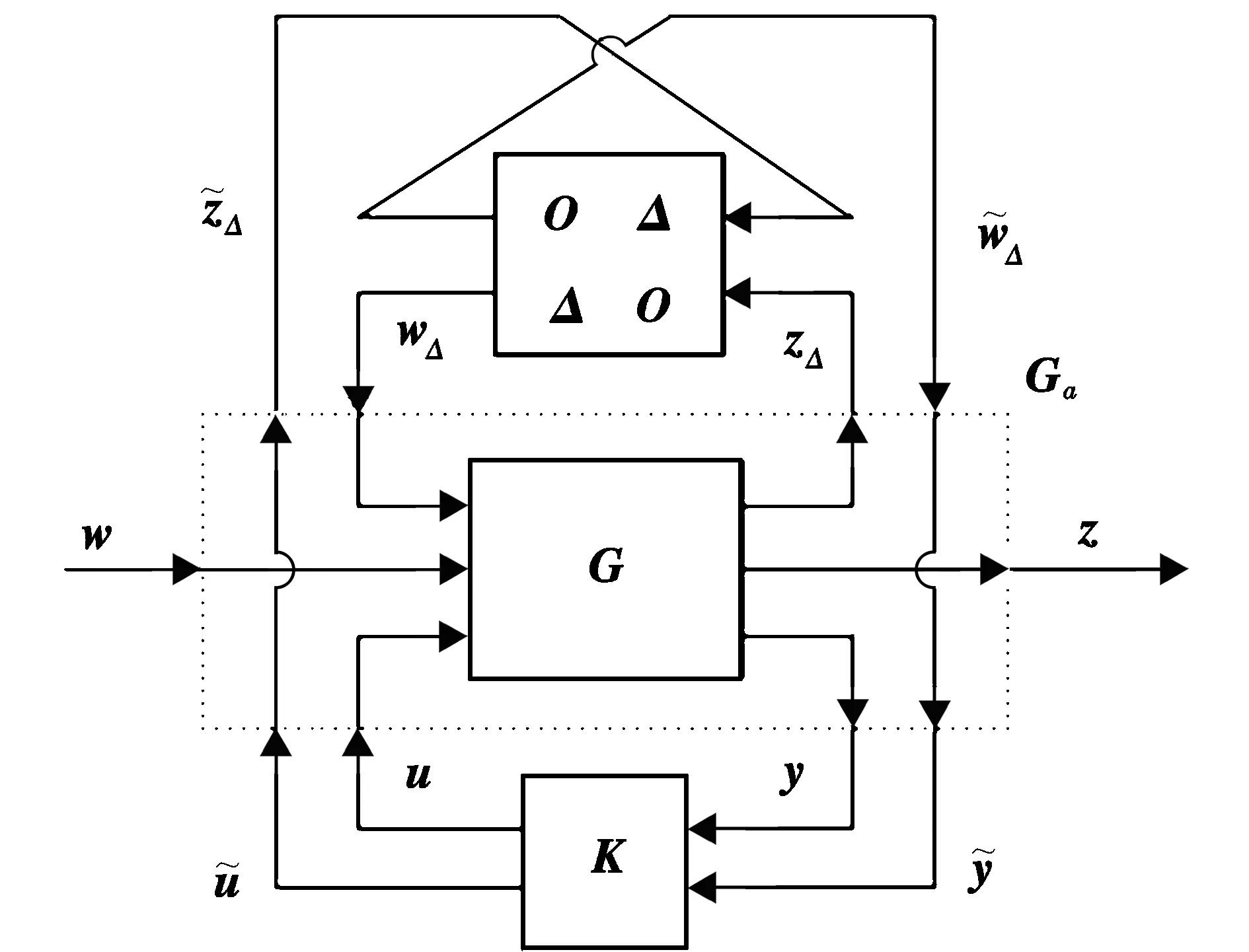
图3 LPV增益调度控制结构图Fig.3 Structure of LPV gain-scheduling control

则由w到z的闭环传递函数矩阵简记为:

Τ(G,K,Δ)=Fl(Fu(G,Δ),Fl(K,Δ))

对变翼导弹而言,由于Δ包含的后掠角、翼展、迎角均可在线获取,故由小增益定理可知,最终的控制问题就是求解矩阵K,使其对于满足ΔTΔ<γ-2的所有变参数Δ,闭环系统内稳定,而且满足条件

max‖T(G,K,Δ)‖∞<γ。

对变翼导弹所具有的快时变不确定特性Δ⨁Δ(重复不确定块),需要先将其标度在有界实引理的适用范围内。定义变翼导弹LPV系统的不确定块对应的标度阵集合为:

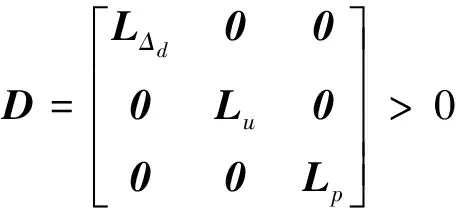
LΔd∈LΔ⨁Δ,Lu∈LΔu,Lp∈LΔp

则采用改进的D-K迭代算法可求得控制器K:

(1)初始化标度矩阵D=I;

(2)构造一个被标度的广义被控对象:

(3)将被控对象转化为GEVP要求的标准形式,并解得时变不确定块LΔd;

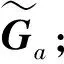
(6)固定K及LΔd,重新构造一个凸优化问题:

minμ=

在每一个频率点处求得使μ极小化的标量ld与矩阵Mu及Mp。

(7)在各频率点处用ld标一化Mu及Mp,并根据标一化Mu及Mp各元素的增益特性拟合出Lu

和Lp。

(8)固定Lu和Lp,并再次更新标度阵D;

(9)重复步骤(2)～(8),直至μ不再减小。

4 非线性联合仿真

仿真方法为基于气动工程计算方法的有控飞行力学联合仿真,该软件可用于快速求解连续变翼过程中导弹的气动特性与多体运动耦合问题,系统结构如图4所示。

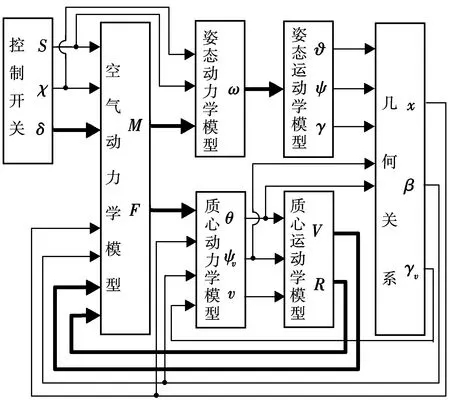
图4 变翼导弹飞行动力学联合仿真系统Fig.4 Collaborative simulation system of flight dynamics of morphing missile

图中的控制关系与空气动力学等模块均不同于传统导弹。控制关系模块用于输出变翼控制量至姿态动力学模块,以耦合弹体旋转角速度模拟惯性附加力矩,而输入空气动力学模块的变翼控制量则主要用于在线计算全弹气动特性。

仿真对象为美国的AMRAAM地空型导弹。变翼展速度为180 mm/s,变后掠速度为45 (°)/s,舵偏限幅为20°,限速为200 (°)/s。

分别取1～3号弹道点:(1 493.3 m,556.1 m/s),(5 298.5 m,629.8 m/s),(8 122 m,700.4 m/s),弹体在两种变翼扰动作用下对方波加速度指令的跟踪效果见图5～图7。

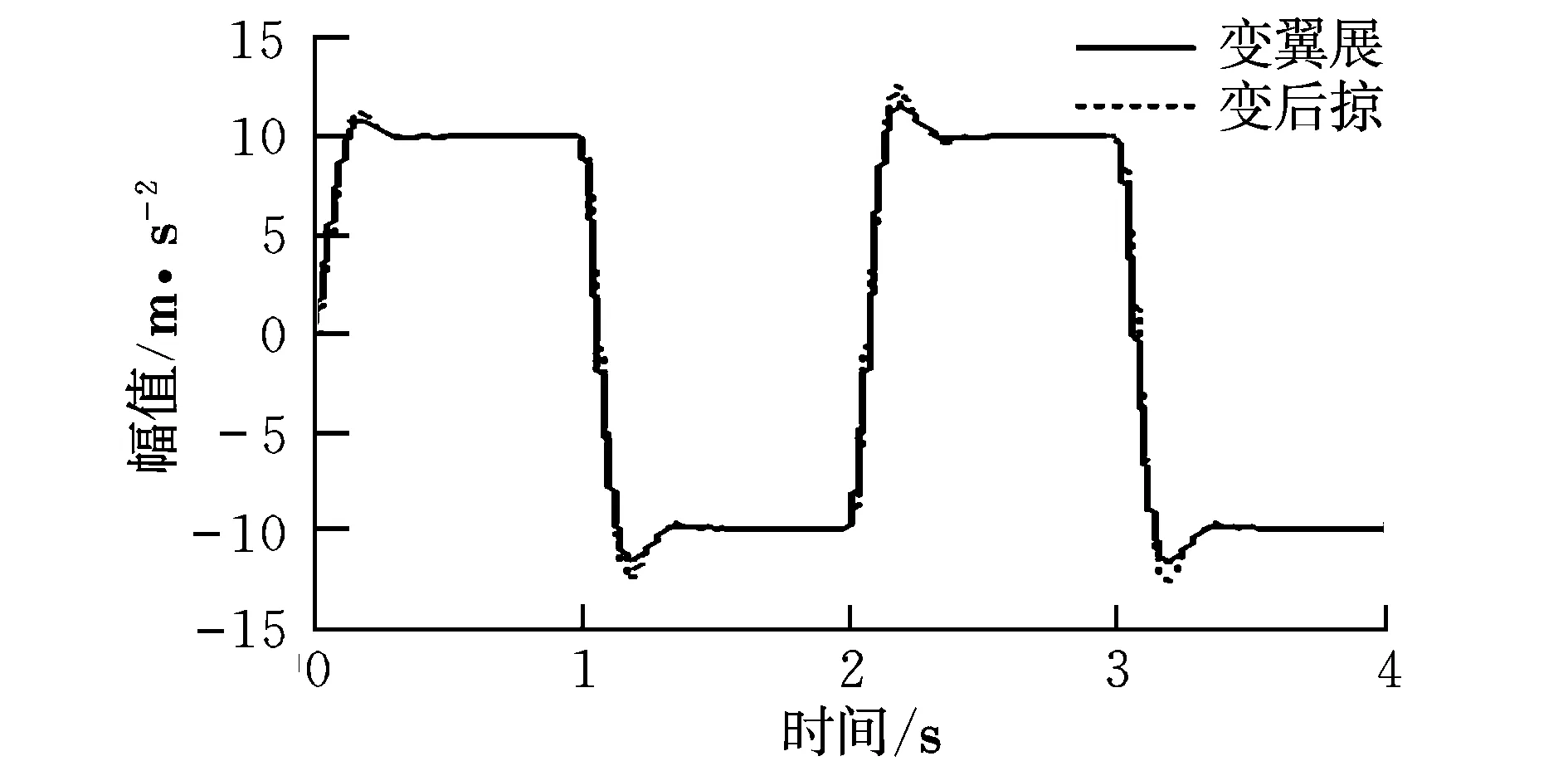
图5 弹道点1的方波响应Fig.5 Missile response to square wave at ballistic point No.1

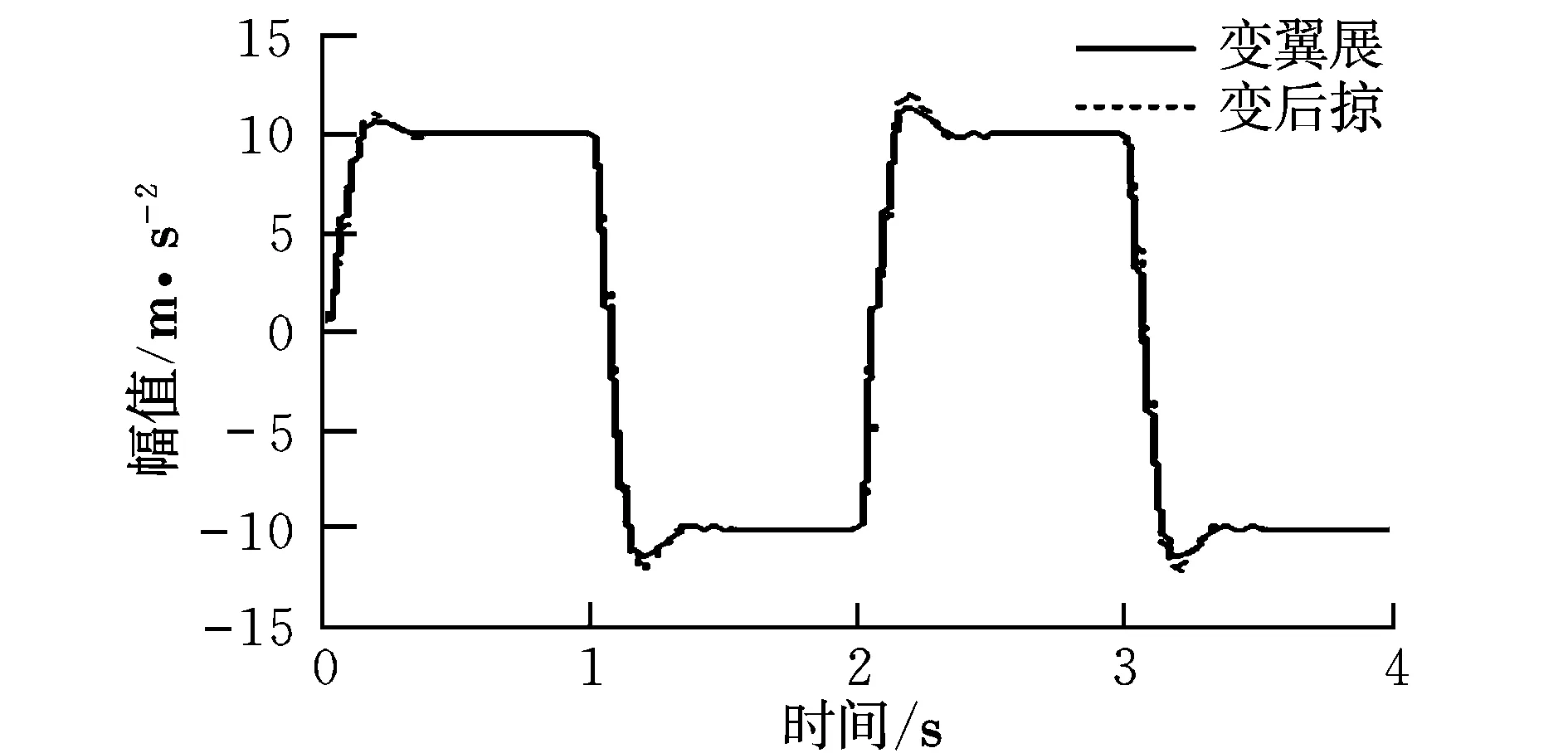
图6 弹道点2的方波响应Fig.6 Missile response to square wave at ballistic point No.2

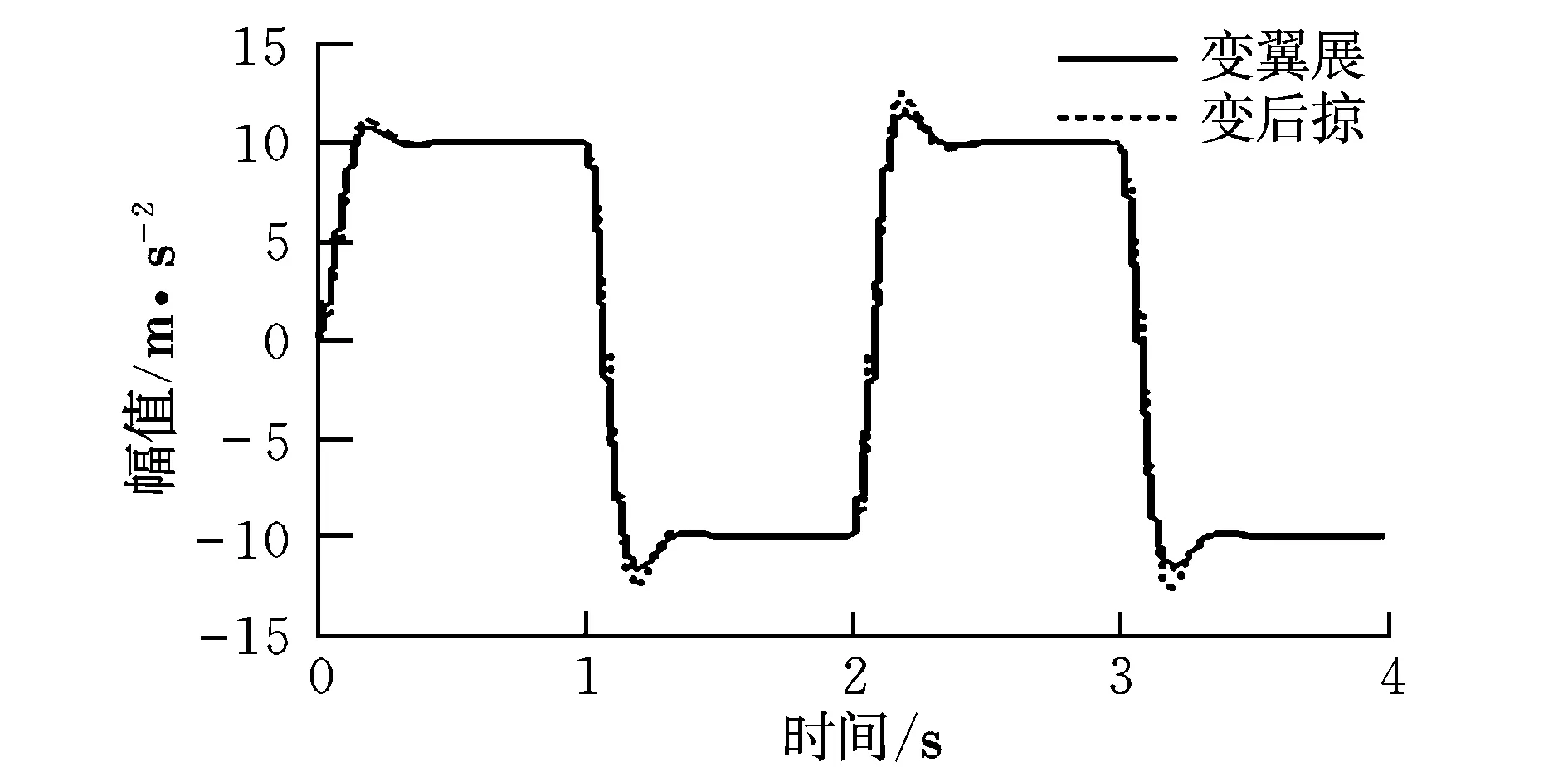
图7 弹道点3的方波响应Fig.7 Missile response to square wave at ballistic point No.3

经测算,3个弹道点的方波响应时间均小于0.45 s,超调量在10%以内,稳态误差为0。可见,通过LPV控制,变翼展及变后掠引起的扰动能得到有效抑制。LPV控制器能适用更广的飞行包线,因为LPV控制器是可以随对象动态时变的,具有自适应扰动和外界不确定的增益调度功能。相比之下,LPV控制器对变后掠的控制品质略低于变翼展形式,原因是弹翼变后掠时,后掠角与翼展是同时变化的,相应惯性和气动特性变化幅度均较大,其对弹体扰动要强于变翼展。

5 结论

(1)采用状态变换法能够对变翼导弹的非线性模型进行准线性化,从而得到较精确的线性参变模型,其形式满足LPV鲁棒控制的要求,能够充分体现变翼诱发的时变惯性及气动不确定性。

(2)将变翼导弹LPV模型中变翼诱发的扰动建模为标称系统的时变不确定性是可行的,所设计的自增益调度非线性控制器对快速变翼具有很强的鲁棒性,能在更大的飞行包线内有效抑制复杂扰动,并实现对过载指令快速而稳定的跟踪。

(3)针对导弹变翼连续气动计算与动态模型的交叉求解难题,提出了一种非线性动力学联合仿真方法,通过对不同变翼方式的操纵响应仿真,验证了其有效性,能够用于变翼导弹,甚至扩展用于其它类型变形飞行器的动力学与控制仿真。

[1] Meurnier M.Viscous CFD analysis of a deflected nose axisymmetric projectile at high speeds [D].Cranfield:Cranfield University,2005.

[2] Takahashi T T,Spall R J,Turner D C.A multi-disciplinary survey of advanced subsonic tactical cruise missile configurations[R].AIAA-2005-0709,2005.

[3] Matthew J Dillsaver,Milton E Franke.Wind tunnel study of oblique wing missile model [R].AIAA-2008-318,2008.

[4] Moti Karpel,Evgeny Selitrennik.Computational aeroelastic simulation of rapid morphing wing-body configuration [R].AIAA-2008-1898,2008.

[5] Bae Jae-Sung,Seigler T Michael,Inman Daniel J.Aerodynamic and aeroelastic considerations of a variable-span morphing wing[R].AIAA-2004-1726,2004.

[6] Seigler T Michael,Bae Jae-Sung,Inman Daniel J.Flight control of a variable span cruise missile [R].IMECE-2004-61961,2004.

[7] Duan Chao-yang,Guo Jian-guo,Zhou Jun.Autopilot design for missile with morphing wings [J].Advanced Computer Theory and Engineering,2010,6(1):520-523.

[8] 丛延.智能可变外形导弹的气动外形总体设计研究[D].西安:西北工业大学,2007.

[9] 王旭刚,周军.变后掠翼战术巡航导弹动力学控制及仿真[J].计算机仿真,2008,25 (6):62-65.

[10] 钱杏芳,林瑞雄,赵亚男.导弹飞行力学[M].北京:北京理工大学出版社,2003:36-39.

[11] 张公平,段朝阳,廖志忠,等.可变形翼战术导弹多体动力学特性[J].弹箭与制导学报,2011,6 (31):149-152.

LPVgain-schedulingcontroloftacticalmissilewithmorphingwings

ZHANG Gong-ping, DUAN Chao-yang, LIAO Zhi-zhong

(Guidance and Control System Department, China Airborne Missile Academy, Luoyang 471000, China)

In missile flight, changing wing’s shape will induce tight coupling of fast-varying aerodynamics and multi-body kinematics. Based on the theorem of momentum and angular momentum of particles system, a set of nonlinear multi-body dynamical model is developed to account for the time-varying characteristics of flight dynamics of morphing missile. The following linear parameter-variable form is deduced by means of states transformation. The improvedD-Kiterative algorithms are used to design LPV gain-scheduling controller for a typical axisymmetric missile with morphing wings. The nonlinear collaborative simulation demonstrates that the robust LPV controller has an excellent control quality and robustness and can be used to stabilize and control flight of morphing missile in large airspace.

morphing wing; tactical missile; multi-body dynamics; gain-scheduling control

TJ765

A

1002-0853(2013)06-0535-05

2013-03-18;

2013-06-18; < class="emphasis_bold">网络出版时间

时间:2013-10-22 14:14

航空科学基金重点资助(2008ZA12001)

张公平(1982-)，男，河南洛阳人，工程师，博士，研究方向为飞行动力学与控制。

(编辑：姚妙慧)