球锥形头罩高超声速绕流流场数值模拟

许东, 李欣, 徐力, 王亚辉

(1.北京航空航天大学 仪器科学与光电工程学院, 北京 100191; 2.北京航天自动控制研究所 宇航与智能控制技术国家级重点实验室, 北京 100854)

球锥形头罩高超声速绕流流场数值模拟

许东1, 李欣1, 徐力2, 王亚辉2

(1.北京航空航天大学 仪器科学与光电工程学院, 北京 100191; 2.北京航天自动控制研究所 宇航与智能控制技术国家级重点实验室, 北京 100854)

研究了不同飞行参数下球锥形光学头罩的高超声速绕流流场的数值模拟问题。首先,分别利用k-ε湍流模型和SA湍流模型求解N-S方程,获得了球锥形光学头罩绕流流场的模拟结果。然后,将模拟结果与风洞测试得到的实验数据进行比较分析。结果表明，在高马赫数、大迎角情况下采用k-ε湍流模型可以得到相对更准确的计算结果。最后,对流场的温度、压强、密度分布特性进行了分析,给出了球锥形头罩绕流流场的压强、温度和密度随飞行参数的变化规律。

球锥形头罩; 流场; 数值模拟; 湍流模型

0 引言

随着现代化战争对导弹飞行速度和突防能力要求的不断提高,高超声速导弹已成为当前的研究热点。导弹头罩与周围气体剧烈作用会形成复杂的流场,进而产生气动光学效应[1],影响光学制导系统对目标的探测、识别和跟踪的能力。球锥形光学头罩具有较好的空气动力学特性,可以减小导弹在高速飞行时受到的空气阻力和摩擦热,现已广泛应用于空空导弹(如“霹雳”7、“杨树”R-27T、“怪蛇”3等)。进行球锥形头罩的绕流流场数值模拟,不仅对研究导弹的气动特性具有重要意义,而且还是实现气动光学效应校正、提高导弹制导精度的关键技术之一。

对流场参数计算的准确性在很大程度上取决于所选择的湍流模型。目前对高速流场的数值模拟主要采用的是k-ε湍流模型和SA(Spalart-Allmaras)湍流模型,并且研究对象主要集中于飞行器整体、翼型、平板形侧窗等[2-7]。如刘景源[4]、于子文[5]利用k-ε湍流模型分别对平板绕流、前飞旋翼流场进行了数值模拟,周大高[6]、段卓毅[7]利用SA湍流模型分别对翼型S825绕流、某机翼副翼舵面流场进行了数值模拟。这些研究都得到了与实验数据吻合较好的计算结果，但是这两种湍流模型对于球锥形头罩高超声速绕流流场是否适用并不确定。因此,本文将首先对这两种湍流模型在计算球锥形头罩高超声速绕流流场数值模拟中的有效性进行讨论;然后通过对模拟结果的分析,研究不同马赫数和不同迎角条件下绕流流场的温度、压强、密度等参数的分布特性,为分析球锥形头罩的气动特性和气动光学效应提供数据依据。

1 计算方法

1.1 控制方程

流体运动的基本方程是建立在质量守恒定律、牛顿运动定律和能量守恒定律的基础上的。习惯上将连续方程、动量方程和能量方程组成的流体运动方程称为N-S方程组。在三维笛卡儿直角坐标系中,可压缩粘性流体N-S方程组的守恒积分形式为:

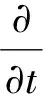
(1)

式中,W为流场守恒矢量;V为任意控制体体积;∂V为控制体边界;H为矢量通量,可分解为无粘对流矢量通量Hc和粘性矢量通量Hv之差的形式;n为∂V表面的单位外法矢量；S为面积。W,Hc,Hv的具体表达式可参见文献[1]。

为封闭方程组,还需引入4个热力学关系式，分别为完全气体状态方程:

p=ρRT

(2)

单位质量气体的总能量:

e=p/[(γ-1)ρ]+ujuj/2

(3)

由Sutherland公式计算得到的动力粘性系数为:

μ=C1T3/2/(T+C2)

(4)

式中,C1=1.458×10-6kg/m·s·K1/2;C2=110.4 K。

对于各向同性流体,其导热系数为:

k=μCP/Pr=μγR/[(γ-1)Pr]

(5)

式中,γ为气体比热系数,对于完全气体通常γ=1.4;R为气体常数;Pr为普朗特数,对于完全气体通常Pr=0.72。

1.2 湍流模型

k-ε二方程湍流模型是由Launder等人在1972年提出的,因其稳定性、经济性和计算精度较高，现已成为湍流模型中应用最广泛、最为人熟知的。SA湍流模型是由Spalart和Allmaras在1992年提出的,是相对简单的一方程模型,对流动分离区附近的计算效果较好,常用于模拟翼形、壁面边界等流动,现已广泛应用于航空领域。

在k-ε二方程湍流模型中,通过求解湍流动能k方程和湍动耗散率ε方程,得到k和ε的解,然后再用k和ε的值计算湍流粘度μt,最终通过Boussinesq假设得到雷诺应力的解。其相应的方程和函数表达式为[8-9]:

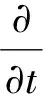
(6)

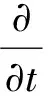
(7)

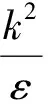
(8)

式中,模型系数Cμ=0.09,Cε1=1.44,Cε2=1.92,σk=1.0,σε=1.3。

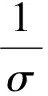
(9)

式中,右边四项分别为湍流粘性的生成项、耗散项、自定义源项和解体项。

(10)

(11)

式(9)～式(11)中的各项具体表达式和模型系数可参见文献[10-11]。

1.3 网格划分

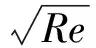
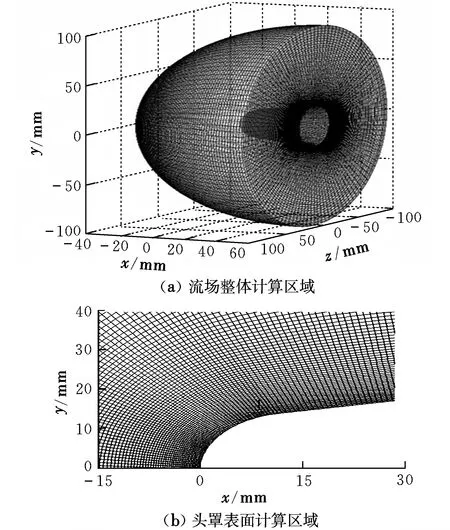
图1 计算网格示意图Fig.1 Scheme of computational grids

1.4 边界条件

上游边界:采用无穷远处自由可压来流作为压力远场边界条件,给定来流的静压、静温和马赫数;出口边界:采用压力出口边界条件,对于达到高超声速的流动,参数都由流场内部通过插值外推得到;物面边界:采用无滑移壁面边界条件。

2 计算结果与分析

2.1 湍流模型有效性分析

以文献[12]中风洞测试的实验条件为输入参数,设来流的初始压强为1.5 MPa,初始温度为370 K,导弹飞行马赫数为5和8,迎角α为0°,5°,10°,15°,对图1中所示光学头罩的绕流流场进行数值模拟。计算过程中分别采用k-ε湍流模型和SA湍流模型对N-S方程进行求解,并将计算得到的头罩表面压力系数与风洞实验测得的头罩表面压力系数进行了比较。

图2和图3中给出了z=0对称截面上头罩表面压力系数沿轴向距离的分布情况,其中Cp0表示风洞实验测得的压力系数,Cp1表示采用k-ε湍流模型时计算得到的压力系数,Cp2表示采用SA湍流模型时计算得到的压力系数。从图中可以看出,当飞行马赫数为5、迎角为0°～15°时,两种模型的计算结果与实验数据吻合程度都比较好;当飞行马赫数为8、迎角为0°和5°时,两种模型的吻合程度也都比较好;但当马赫数为8、迎角为10°和15°时,k-ε湍流模型的计算结果比SA湍流模型的计算结果更为准确。这是由于SA模型运输方程中的常系数是基于简单流动分析得到的,在这些简单流动中湍流运输特性一般处于平衡状态。但在高马赫数、大迎角情况下湍流的非平衡运输现象明显,湍流粘性的生成和耗散之间的平衡关系发生了改变,导致计算结果出现了偏差。可见在飞行条件较为苛刻的情况下,k-ε湍流模型比SA湍流模型更为适合。

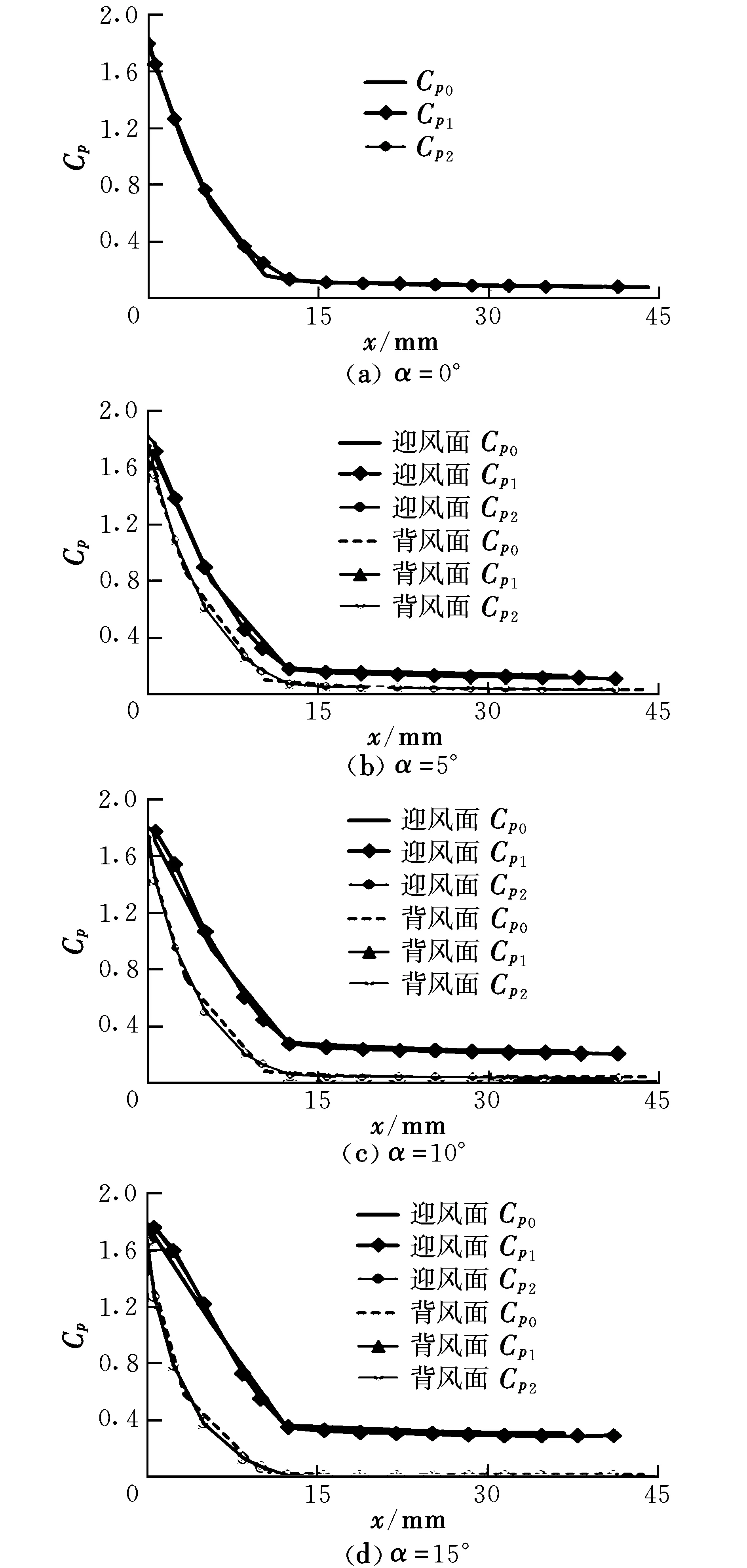
图2 Ma=5时压力系数分布Fig.2 Distribution of the pressure coefficient when Ma=5

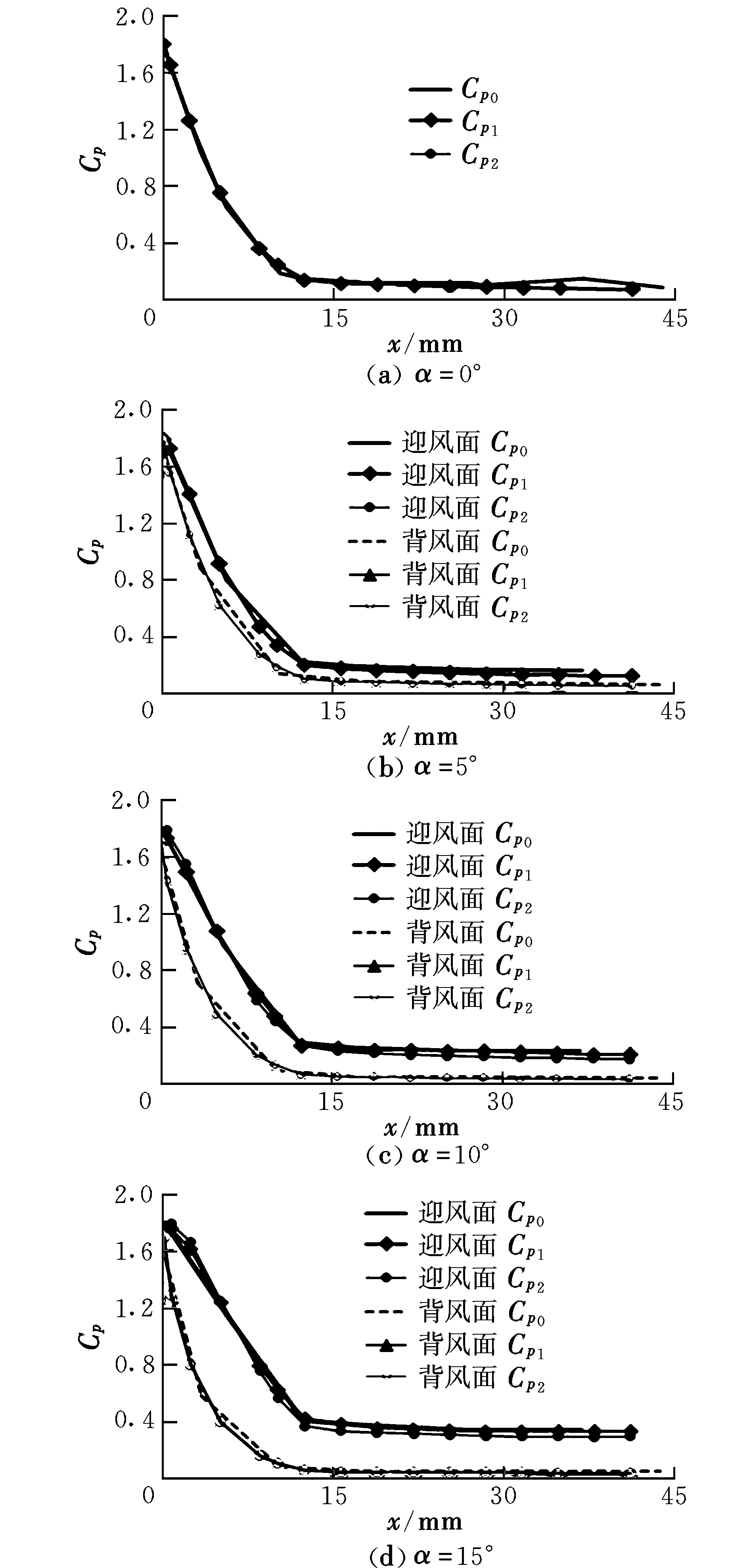
图3 Ma=8时压力系数分布Fig.3 Distribution of the pressure coefficient when Ma=8

2.2 流场参数的分布情况

以飞行高度为5 km、马赫数分别为5和8、迎角分别为0°和15°的飞行参数为例,利用k-ε湍流模型对光学头罩的绕流流场进行了数值模拟。图4～图6给出了z=0对称截面上头罩周围流场的压强、温度、密度的等值分布云图。从图中可以看出,头罩顶部区域的压强、温度、密度都最大,在Ma=5时压强高达1.6 MPa,温度高达1 500 K,密度高达4 kg/m3;在Ma=8时则分别高达4 MPa,3 500 K,4.5 kg/m3。这是由于来流与光学头罩相遇时受到强烈压缩,压强、密度大为增加;空气本身又具有粘性,与头罩表面相接触时受到阻滞,使得气流的速度大为降低,在头罩表面附近形成边界层,在边界层内来流的动能几乎全部转化为内能,使光学头罩周围的气流温度迅速升高。而头罩后部的流场充分发展为湍流,形成弓形脱体激波,分子运动耗散掉湍动能,使得压强、温度、密度都有所降低。

同时从图中还可以看出,随着迎角的增加,驻点位置逐渐移至迎风面,头罩弓形激波在迎风面更加贴近物面,脱体距离减少,同一位置对应的压强、温度、密度都有所增大;在背风面激波则远离物面,脱体距离增大,同一位置对应的压强、温度、密度有所减小。另外,随着马赫数的增大,同一位置对应的压强、温度、密度都有所增大,激波脱体距离有所减小。

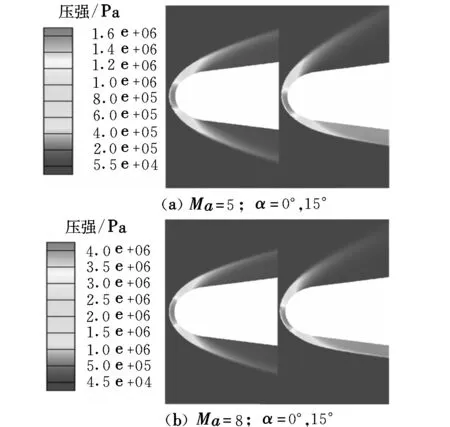
图4 压强分布云图Fig.4 Contour map of pressure

图5 温度分布云图Fig.5 Contour map of temperature

图6 密度分布云图Fig.6 Contour map of density

3 结束语

本文的分析表明,利用数值计算的方法模拟光学头罩高超声速绕流流场是有效的,且在高马赫数、大迎角情况下采用k-ε湍流模型计算得到的结果比采用SA湍流模型计算得到的结果更为准确。通过分析不同飞行速度、不同迎角情况下流场压强、温度、密度等参数的分布情况可以看出,头罩顶部驻点位置的压强、温度、密度最大。由此可知，此处的气动加热效应和热辐射效应最为严重,对光传输及目标成像的影响最为明显,需重点研究气动光学效应的校正方法。此外,在大迎角飞行时,迎风面的压强、温度、密度较大,也需考虑气动光学效应的影响。

总的来说,数值模拟方法与风洞实验相比更具有灵活性和经济性,针对导弹不同的飞行参数,只需改变计算的初始条件、边界条件即可得到相应的数值解算结果,从而为定量研究球锥形头罩的气动特性和气动光学效应提供数据支持。

[1] 殷兴良.气动光学原理[M].北京:中国宇航出版社,2003:55-62.

[2] Tilmann C P,Buter T A,Bowersox R D W. Characterization of the flowfield near a wrap-around fin at mach number 2.8 [R].AIAA-97-0522,1997.

[3] 陈澄,费锦东.侧窗头罩高速层流流场光学传输效应数值模拟[J].红外与激光工程,2005,34(5):548-552.

[4] 刘景源,李椿萱.基于Reynolds平均的高超声速二方程湍流模型[J].航空学报,2008,29(1):28-33.

[5] 于子文,曹义华.前飞旋翼三维湍流场的数值模拟[J].北京航空航天大学学报,2006,32(7):751-755.

[6] 周大高,柳阳威.改进SA模型对翼型分离流动的数值模拟[J].北京航空航天大学学报,2012,38(10):1384-1388.

[7] 段卓毅,王小震,陈迎春.三维舵面绕流的N-S方程计算研究[J].飞行力学,2007,25(3):67-70.

[8] Jones W P,Launder B E.The prediction of laminarization with a two-equation model of turbulence[J].Journal of Heat and Mass Transfer,1972,15(2):301-314.

[9] Jones W P,Launder B E.The calculation of low-reynolds number phenomena with a two-equation model of turbulence[J].Journal of Heat and Mass Transfer,1973,16(6):1119-1130.

[10] Spalart P R,Allmaras S R.A one-equation turbulence transport model for aerodynamic flows[R].AIAA-92-0439,1992.

[11] Paciorri R,Dieudonne W,Degrez G,et al.Validation of the spalart-allmaras turbulence model for application in hypersonic flows[R].AIAA-97-2323,1997.

[12] 李素循.典型外形高超声速流动特性[M].北京:国防工业出版社,2007:80-109.

Numericalsimulationofhypersonicflowfieldsaroundsphere-cone-shapeddome

XU Dong1, LI Xin1, XU Li2, WANG Ya-hui2

(1.School of Instrument Science and Opto-electronics Engineering, BUAA, Beijing 100191, China; 2.National Key Laboratory of Science and Technology on Aerospace Intelligence Control, Beijing Aerospace Automatic Control Institute, Beijing 100854, China)

The numerical simulation of hypersonic flow fields around sphere-cone-shaped dome under different flight conditions was studied. Firstly, by separately applyingk-εturbulence model and SA (Spalart-Allmaras) turbulence model to solve the N-S equations, the flow fields around sphere-cone-shaped optical dome were simulated. Secondly, the simulation results were compared with related experimental data, and the comparison shows that, under the condition of high Mach number and attack-angle more accurate calculation results can be obtained when usingk-εturbulence model. Lastly, the distribution of pressure, temperature and density of the flow fields around sphere-cone-shaped dome was analyzed, and the variation of the three parameters with flight condition was also presented.

sphere-cone-shaped dome; flow fields; numerical simulation; turbulence model

V211.3

A

1002-0853(2013)06-0491-05

2013-03-29;

2013-09-01; < class="emphasis_bold">网络出版时间

时间:2013-10-22 14:15

国家自然科学基金资助(61378077)

许东(1973-)，男，江苏徐州人，副教授，博士，主要研究方向为气动光学效应及目标探测识别；

李欣(1988-)，女，山东济南人，硕士研究生，主要研究方向为气动光学及流场仿真。

(编辑：姚妙慧)