平板翼型地面效应数值模拟与分析
2013-11-04陈世适熊芬芬
陈世适, 熊芬芬
(北京理工大学 飞行器动力学与控制教育部重点实验室, 北京 100081)
平板翼型地面效应数值模拟与分析
陈世适, 熊芬芬
(北京理工大学 飞行器动力学与控制教育部重点实验室, 北京 100081)
目前大多数有关地面效应的研究仅限于平直地面,并非现实中更为普遍的弯曲地面,从而极大地影响了研究结果的有效性。对靠近地面的二维平板翼型升力变化情况进行了研究,包括平直地面、山谷和山坡弯曲地面,采用复变函数理论计算流场中的复速度,同时运用保角变换将平板绕流变换为圆柱绕流,并且采用离散涡法建立了地面数学模型,将其表示为一系列离散边界元。研究结果表明,当平板翼型靠近平直地面时,其升力明显增大;当其飞过山谷或山坡时,其升力波动相当激烈,故在设计地效飞行器时应妥当考虑和处理此现象。
地面效应; 弯曲地面; 复变函数; 保角变换; 离散涡
0 引言
当飞行器从地面起飞或者降落至地面时,由于此时飞行器非常接近地面,其机翼周围气流的流场有所变化,作用在飞行器上的升力、阻力及俯仰力矩也发生了变化,该现象称之为地面效应[1-2]。目前,有关地面效应的研究甚多。Wieselsberger[3]首次使用镜像法对地效飞行器进行了研究,Tomotika等人[4]基于单翼翼型的结果对靠近平直地面的平板翼型升力进行了理论计算研究,Ivanteeva等人[5]研究了靠近地面的特定翼型的气动特性,Terentiev等人[6]使用数值方法对靠近地面翼型的流场进行了仿真研究,张亮等人[7]对二维地效翼气动力进行了计算和性能研究,李盾和王义宁[8]对地效飞行器三维地面效应进行了数值模拟。最近,王中清等人[9]对飞行器地面效应定常/非定常流场进行了数值模拟。
然而,以上研究多数仅限于平直地面,鲜有对弯曲地面进行研究。现实中机场周围的地形并非都是平坦的,时常伴有山谷或者山坡,机场跑道也偶尔有凸起或者凹坑。当飞行器起飞或者降落时,机翼与跑道地面之间的距离将随着地面形状而改变,导致飞行器升力波动,从而影响飞行器的安全系数。
本文将对靠近平直和弯曲地面的平板翼型升力变化情况进行研究。首先将平板翼型周边流场描述为平面势流,通过复变函数理论可求得流场的速度势与流函数;然后运用保角变换将平板绕流变换为圆柱绕流,同时采用离散涡法处理地面对流场的影响,在地表面散布一系列离散点涡,将连续的地面问题转换为离散的边界元问题。该方法比其它数值方法更能节省计算时间,并可运用于各种形状的复杂弯曲地面问题。文中首先对平直地面情况进行研究以验证上述方法的有效性,然后将上述方法应用于弯曲地面情况,可求得翼型高度以及地面弯曲半径对平板翼型升力的影响。
1 数学模型及解决方法
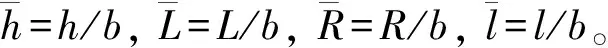

图1 山谷弯曲地面简化原理图Fig.1 Simplified schematic diagram of hollow (<0)
不可压流体的任何一种平面势流必定具有一个确定的复势W(z)=φ(x,y)+iψ(x,y),其中,φ(x,y)和ψ(x,y)分别为速度势和流函数[10]。研究中采用儒可夫斯基变换z=(ζ+c2/ζ)/2(c为实常数),其能够将在z平面中平板绕流变换为在相应ζ平面中圆柱绕流[10-11],有利于将已知的圆柱绕流研究结果运用于平板翼型的研究。
假定沿着x和y方向的速度分别为u和v。根据复变函数理论,地面中每个控制点在直匀流和点涡流中的复速度为[11]:

(1)
根据离散涡法,地面可分为n个边界单元,同时每个边界单元都含有一个控制点和点涡。其中,控制点位于边界单元长度的1/4处,而点涡位于3/4处,jth个点涡的强度为Γj(见图1)。受到地面的约束,地面中每个控制点的法向速度都为零,且其计算可分为两部分:受到地面上方直匀流的影响;受到地面中分布离散点涡的影响。
由圆定理可知,在ζ二维平面直匀流和点涡流中,圆柱体无环量流动的复势函数可分别表示为[11]:
(2)
(3)
式中,V∞为无边界直匀流的复速度;Rc为平板翼型保角变换至ζ平面的圆半径;Γ为点涡的强度;ζv为点涡在ζ平面的位置。
式(4)表示ith控制点在jth点涡流中复速度的简化形式,其中Ai,j定义为jth点涡对ith控制点复速度的影响因子。
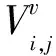
(4)
为了满足库塔-儒可夫斯基假设(K-J条件),平板翼型的后缘应当为一个额外的控制点(n+1),其沿翼面的法向速度由于受到翼型表面的影响也为零,同时需要在ζ平面的原点处添加一个额外环绕翼型的环量Γn+1。汇总直匀流和所有点涡流,ith控制点在流场中的总复速度为:
=ui-ivi(i,j=1,2,…,n,n+1)
(5)
由于受到地面和K-J条件的约束,每个控制点的法向速度都为零。
对于平直地面情况,根据几何关系(见图2),该区域控制点在流场中的法向速度可表示为:
Vi,n= -uisinα+vicosα=0
(i=1,2,…,n+1)
(6)

图2 平直地面上控制点的法向速度Fig.2 Normal speed of control point on flat ground
对于山谷与山坡弯曲地面情况,根据它们不同的几何关系(见图3和图4),对应区域控制点的法向速度为:
Vi,n=uicos(θi+α)+visin(θi+α)=0
(θi=0~π 且i∈山谷地面)
(7)
Vi,n= -uicos(θi-α)+visin(θi-α)=0
(θi=0~π 且i∈山坡地面)
(8)

图3 山谷部分控制点的法向速度Fig.3 Normal speed of control point in hollow

图4 山坡部分控制点的法向速度Fig.4 Normal speed of control point on hill
故可通过解式(6)~式(8)获得每个点涡的强度Γj。根据流场中的叠加性,在靠近地面和满足K-J条件的情况下,平板翼型周围流场的复势函数可表示为:


图5 平板翼型靠近平直地面、山谷与山坡 弯曲地面时的流线图 Fig.5 Streamlines around plate airfoil near flat ground, hollow and hill
环绕平板翼型的全部涡环量可以通过闭环积分计算可得。

根据K-J理论,单位翼展长度的升力系数可表示为:

式中,ρ和V∞分别为流体的密度和直匀流的速度。
为了能清晰地显示地面对翼型升力系数大小的影响,可额外定义一个新的无量纲参数,即翼型在有边界流和无边界流中升力系数的比值:
2 仿真结果及分析
2.1 平直地面
(1)迎角对翼型升力大小的影响


图6 迎角对升力系数的影响Fig.6 Influence of angle of attack on lift coefficient
(2)平板翼型离平直地面高度对升力大小的影响


图7 翼型高度对升力系数的影响Fig.7 Influence of airfoil height on lift coefficient

2.2 弯曲地面
(1)地面弯曲半径对翼型升力系数的影响

图8 山谷弯曲半径对升力系数的影响Fig.8 Influence of hollow radius on lift coefficient
由图5(b)可见,当流体流过山谷弯曲地面的上表面时,流场的速度方向沿着地面的形状,先降低后爬升。因此,当平板翼型位于山谷的右边时,其迎角由于流场速度的上升而变大,从而导致升力的增加。相反地,当平板翼型位于山谷的左边时,其迎角由于流场速度的下降而变小,从而导致升力减小。而且,由于山谷会增大周围流场空间,将导致山谷周围的流场速度降低,进而也引起升力减小。
(2)平板翼型离弯曲地面高度对升力大小的影响
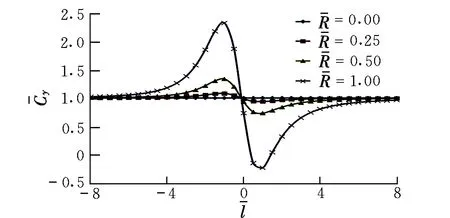
图9 山坡弯曲半径对升力系数的影响Fig. 9 Influence of hill radius on lift coefficient

图10 翼型高度在山谷情况下对升力系数的影响Fig.10 Influence of airfoil height on lift coefficient for hollow

图11 翼型高度在山坡情况下对升力系数的影响Fig.11 Influence of airfoil height on lift coefficient for hill
3 结束语
本文采用复变函数理论、保角变换法和离散涡法,对平板翼型靠近平直和弯曲地面时引起升力变化的情况进行了研究。由研究结果可知,当平板翼型飞过平直地面时,其升力由于受到地面影响会相对增大,并且升力增量随着迎角的增大而减小,但是当翼型的迎角增大至平衡迎角后,翼型升力反而比其在对应无边界流中的升力还要小。平板翼型越接近弯曲地面,其升力波动越严重,而且,当山谷或山坡地面的弯曲半径越大时,其对平板翼型的升力扰动也越大。如果平板翼型以较小迎角飞过弯曲地面的上表面时,其可能会产生负升力现象,加大了飞行器起飞或降落时坠落的危险性。虽然本文仅对实际工程中使用较少的平板翼型进行了研究,但研究结果对将来地效飞行器的研究具有一定的参考价值。
[1] 林海.飞机地面效应及其试飞方法[J].飞行力学,1996,14(4):52-58.
[2] 秦绪国,刘沛清,屈秋林,等.三维多段机翼地面效应数值模拟[J].航空学报,2011,32(2):257-264.
[3] Wieselsberger C.Wing resistance near the ground[R].NASA TM-77,1922.
[4] Tomotika S,Nagamiya T,Takemouti Y.The lift on a flat plate placed near a plane wall with special reference to the effect of the ground upon the lift of a monoplane aerofoil[J].Proceedings of Aeronautical Research Institute,1933,97(8):1-60.
[5] Ivanteeva L G,Konovalov S I,Pavlovets G A.Calculation of aerodynamic characteristics of the foil near the ground for given magnitudes of its geometric parameters[J].Proceedings of Central Aerohydrodynamics Institute,1980,11(2):1-9.
[6] Terentiev A G,Kartuzova T V.Numerical investigation of flow over airfoil near the ground[J].Proceedings of the National Academy of Sciences and Arts of the Chuvash Republic,1996,(6):94-104.
[7] 张亮,陈萌萌,吴德铭.二维地效翼气动力的计算和性能研究[J].船舶力学,2000,4(2):1-5.
[8] 李盾, 王义宁.地效飞行器三维地面效应的数值模拟[J].飞行力学,2006,24(2):18-21.
[9] 王中清,白俊强,王元元.飞行器地面效应定常/非定常流场数值模拟[J].科学技术与工程,2012,12(5):1073-1075.
[10] Houghton E L,Carpenter P W.Aerodynamics for engineering students (5th edition)[M].Great Britain,Oxford:Butterworth-Heinemann,2003:160-171.
[11] 周云龙,郭婷婷.高等流体力学[M].北京:中国电力出版社,2008:26-32;67-75.
Numericalsimulationandanalysisonaerodynamicsofflatplateairfoilingroundeffect
CHEN Shi-shi, XIONG Fen-fen
(Key Laboratory of Dynamics and Control of Flight Vehicle, Ministry of Education, BIT, Beijing 100081, China)
At present, only the flat ground surface problem is investigated in most studies of ground effect, which is not effective for practical applications due to the universal existence of curved ground surface. In this paper, the lift calculation of a two-dimensional flat plate airfoil placed near the ground surface is investigated, including flat ground surface, hollow and hill curved ground surface. In order to calculate the complex velocity in the flow field, the complex variable function theory is employed. The conformal mapping method is applied to transform the flat plate flow to a flow around a circle cylinder. Moreover, the discrete vortices method is modified to convert the curved ground surface to a series of discrete boundary elements. It is shown that, when the flat plate airfoil flies close to the flat ground, its lift increases obviously. In addition, the lift fluctuation of the flat plate airfoil located near a hollow or a hill is considerably serious, which should be considered during the design of ground effect vehicle.
ground effect; curved ground surface; complex variable function; conformal mapping; discrete vortices
V211.4
A
1002-0853(2013)06-0486-05
2013-03-22;
2013-06-16; < class="emphasis_bold">网络出版时间
时间:2013-10-22 14:13
国家自然科学基金资助 (51105034;10972034)
陈世适(1987-),男,广东湛江人,博士研究生,研究方向为飞行器总体设计;
(编辑:姚妙慧)
