一类非线性四阶微分方程三点边值问题的可解性

施恂栋, 刘文斌

(1.江苏省口岸中学, 江苏 泰州 225321; 2.中国矿业大学 理学院数学系, 江苏 徐州 221008)

一类非线性四阶微分方程三点边值问题的可解性

施恂栋1, 刘文斌2

(1.江苏省口岸中学, 江苏 泰州 225321; 2.中国矿业大学 理学院数学系, 江苏 徐州 221008)

考察了非线性四阶三点边值问题的解和正解的存在性. 其中允许非线性项有一个负的下界. 主要结论表明该问题可以具有正解, 只要非线性项在某些有界集上所满足的条件是适当的.

四阶三点边值问题; 半正非线性; 解和正解; 存在性

0 引言

本文的目的是考察下列非线性四阶三点边值问题的解和正解的存在性.

(1)

本文总是假设Mgt;0,f:[0,1]×[-kM,+∞]→[-M,+∞]是连续的.

1 预备知识

引理1 1)G:[0,1]×[0,1]→[0,+∞)连续;

定义g(t,l)=f(t,l)+M, (t,l)∈[0,1]×[-kM,+∞),则g:[0,1]×[-kM,+∞)→[0,+∞)是连续的, 考察三点边值问题

(2)

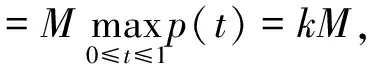
(i) 算子T:C+[0,1]→C[0,1]有定义并且连续;

(ii) 对于任何x∈C+[0,1], (Tx)(0)=(Tx)′(0)=(Tx)″(η)=(Tx)‴(1)=0.

简单核验后, 我们得到

引理2 1)x*是问题(1)的解当且仅当x*+x0是(2)的解；

设q(t)=min{ηt,2ηt-t2}, 0≤t≤1. 由文 [6], 我们有

(3)

则K是C[0,1]中的一个非负函数锥,设

直接计算后,我们得到 :

因此, 0lt;Alt;B.

本文将使用下列控制函数, 对lgt;0, 我们记

Φ(l)=max{g(t,c-x0(t)):(t,c)∈[0,1]×[0,l]}=

max{f(t,c-x0(t)):(t,c)∈[0,1]×[0,l]}+M

Ψ(l)=min{g(t,c-x0(t)):(t,c)∈[μ,ν]×[σl,l]}=

min{f(t,c-x0(t)):(t,c)∈[μ,ν]×[σl,l]}+M

显然有Φ(l)≥Ψ(l).

引理3[3]G(t,s)≥q(t)J(s), (t,s)∈[0,1]×[0,1].

引理4[3]T:C+[0,1]→K是全连续的.

2 主要结果

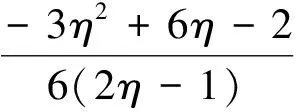
证明因为Alt;B, 容易看出a≠b, 不失一般性, 假设alt;b. 记

Kl={x∈K:‖x‖lt;l}, ∂Kl={x∈K:‖x‖=l},

如果x∈∂Ka, 则‖x‖=a, 0≤x(t)≤a, 0≤t≤1, 于是

0≤g(t,x(t)-x0(t))≤Φ(a)≤aA, 0≤t≤1.

根据引理4,我们有

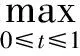
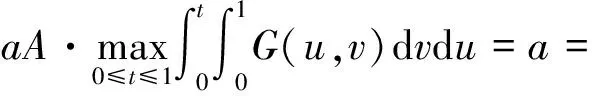
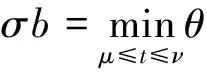
于是g(t,x(t)-x0(t))≥Ψ(b)≥bB,μ≤t≤ν,则有

1) 当0lt;t≤η时

所以x0(t)-aθ(t)lt;0, 即当0lt;t≤η时,H(t)lt;0.

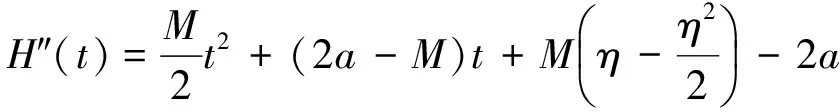
所以

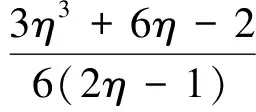
由(1),(2)可知在(0,1]上,H(t)lt;0即x0(t)-aθ(t)lt;0, 现在, 对于0lt;t≤1,

x*(t)=x*(t)+x0(t)-x0(t)≥θ(t)‖x*+x0‖-x0(t)≥aθ(t)-x0(t)gt;0,

因此, 是一个正解, 定理得证.

[1] Gupta C P. Solvability of a three-point nonlinear boundary value problem for a second order ordinary differential equations[J]. J Math Anal Appl, 1992 (168):540-551.

[2] Feng W, Webb J R L. Solvability of a three-point Nonlinear Boundary Value Problem at Resonance[J]. Nonlinear Analysis, 1997, 30(6):3227-3238.

[3] Yao Q L. Existence of positive solutions for a third-order boundary value problem with semipositone nonlinearity[J]. Journal of Mathematical Research and Exposition, 2003, 23(4): 591-596.

[4] 葛渭高. 非线性常微分方程边值问题[M]. 北京: 科学出版社, 2007.

[5] 葛渭高, 李翠哲, 王宏洲. 常微分方程与边值问题[M]. 北京: 科学出版社, 2008.

SolvabilityofAThree-pointNonlinearBoundaryValueProblemforAForthorderDifferentialEquations

SHI Xun-dong1, LIU Wen-bin2

(1.Kouan High School of Jiangsu Province, Taizhou Jiangsu 225321, China)(2.Department of Mathematics, China University of Mining and Technology, Xuzhou Jiangu 221008, China)

The existence of solutions and positive solutions is considered for a nonlinear forth-order three-point boundary value problem where nonlinear is allowed to have a negative lower bound.The main results show that the problem may possess positive solutions provided the conditions of nonlinear term are appropriately satisfied on some bounded sets

forth-order three-point boundary value problem; semipositone nonlinearity; solution and positive solution; existence

2013-03-01

国家自然科学基金资助项目(10771212)

施恂栋(1983-), 男, 江苏兴化人, 硕士, 研究方向为常微分边值问题．

O175

A

1671-6876(2013)02-0095-04

[责任编辑李春红]