具有约束条件的均衡规划问题的微分方程方法

王 莉，王虎彬，王诗云，孙菊贺

（沈阳航空航天大学 理学院，沈阳 110136）

0 引 言

具有约束条件的均衡规划问题是指：求解x＊∈Ω满足

其中Φ：Rn×Rn→R，g：Rn→Rm是两个映射；Ω⊆Rn是一闭凸集。假设Φ（x，y）对于任意的x∈Ω在y∈Ω处是凸的，向量值函数g（y）的每个分量函数都是凸的。假设极值映射≤0，y∈Ω｝对任意的x∈Ω都是定义好的，并且原问题（1）的解集Ω＊⊂Ω是非空的。根据文献AUBEN和EKELAND［1］可知，如果Ω是凸紧致的且Φ（x，y）在x处是下半连续的在y处是凸的，则上述最后的假设可成立。

许多著名的问题，如文献NIKAIDO和ISODA［2］及VENETS［3］研究的鞍点问题，文献ANTIPIN［4］研究的在Nash均衡条件下的n人博弈问题，以及ANTIPIN等［5］提出的许多优化反问题等都可以转化为具有约束条件的均衡规划问题，这使得关于具有约束条件的均衡规划问题的求解方法的研究成为一项重要的任务。赵新斌等［6］运用Douglas－Rachford分离技巧解决了具有线性约束的最小矩阵秩优化问题。由ARROW 等［7］，FIACCO等［8］与EVTUSHENKO［9］所提出的微分方程方法在求解优化问题时起着非常重要的作用。微分方程方法是将一个约束优化问题转化为一个微分方程系统，当微分方程中的参量t趋于无穷大时，微分方程系统的解就会收敛于优化问题的解。这一经典的微分方程方法已被许多学者进行研究［10－15］。

本文运用微分方程方法的思想求解具有约束条件的均衡规划问题。运用拉格朗日函数和投影算子，将具有约束条件的均衡规划问题（1）转化为方程组。运用该方程组建立具有控制过程的微分方程系统，并证明了该微分方程系统的解的全局收敛性。最后，运用具有控制过程的微分方程系统求解了2个算例，并描绘了每个算例的微分方程系统的解的轨迹图，从而说明了微分方程方法求解具有约束条件的均衡规划问题的可行性。

下面介绍ANTIPIN［4，15］所提出的斜对称函数的定义及其性质。

定义1［4］称函数Φ（x，y）：Rn×Rn→R是斜对称的，如果满足下面的不等式

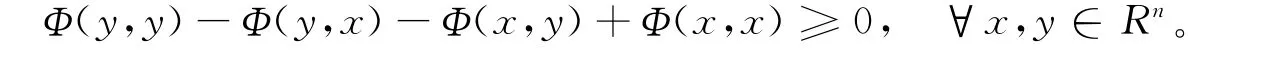
性质1［15］如果函数Φ（x，y）：Rn×Rn→R是斜对称的且关于第二元是凸的，则其关于第二元的梯度▽yΦ（x，x）是单调的，即有

到凸集上的投影算子在将具有约束条件的均衡规划（1）转化为方程组的过程中起着非常重要的作用，这里关于投影算子的定义不做回顾，只介绍其重要性质：

引理1［8］设H是一个实Hilbert空间，C是一闭凸子集。对于给定的z∈H，u∈C满足不等式〈z－x，x－u〉≥0，∀x∈C当且仅当u＝ΠC（z），其中ΠC是H到C上的一个投影。

1 微分方程系统

运用拉格朗日函数和投影算子，建立微分方程系统，并证明微分方程系统的解的收敛性。

具有约束条件的均衡规划问题的拉格朗日函数为

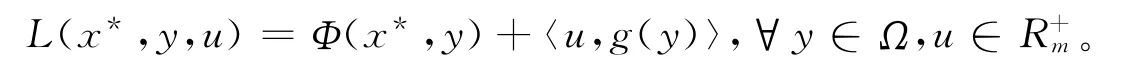
如果函数的约束条件是正则的，则该问题可转化为拉格朗日函数L（x＊，y，u）的鞍点问题，即

如果g（y）是可微的，上面的不等式系统可转化为下面的变分不等式

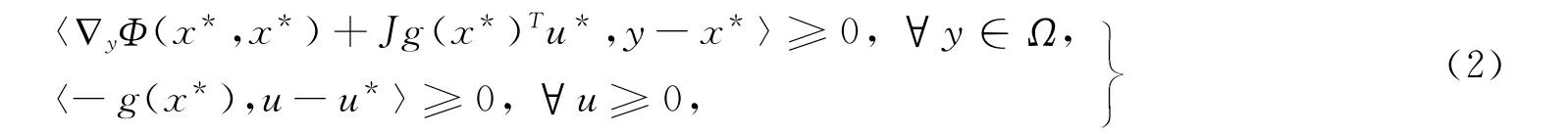
其中，Jg（x＊）是映射g在x＊处的Jacobian阵。

根据引理1上述的变分不等式组（2）可等价地表示成下面的方程组

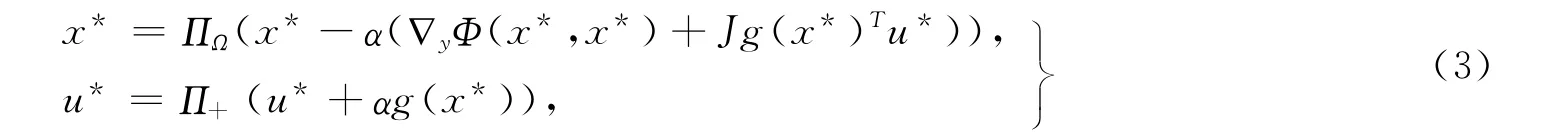
其中参数α＞0，ΠΩ和Π＋分别是向量到集合Ω和正卦限Rn＋上的投影算子。

根据上面的方程组（3）可以建立下面的具有控制过程的微分方程系统

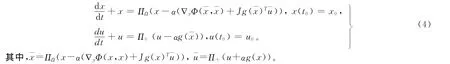
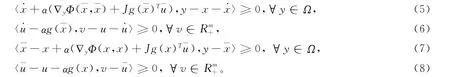
如果映射g，∇yΦ和JgT均是Lipschitz连续的，且Lipschitz常数分别是｜g｜，｜∇yΦ｜和｜Jg｜，而且‖‖≤C0，其中C0是一个常数，则容易得到下面的估计式

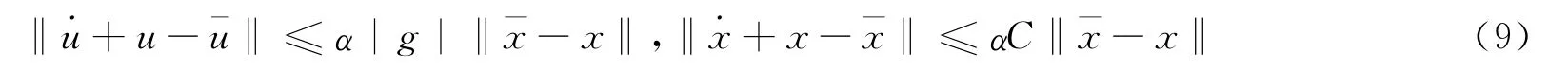
成立，其中C＝｜∇yΦ｜＋C0｜Jg｜。

由于向量值函数g（y）的每个分量函数都是凸的，（2）的第一式可转化为下式

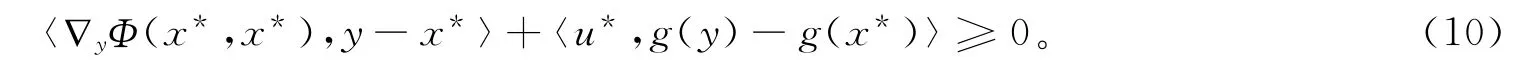
下面证明具有控制过程的微分方程系统（4）的解的聚点是具有约束条件的均衡规划问题（1）的解。

定理1 设具有约束条件的均衡规划问题（1）的解集Ω＊是非空的，Φ是斜对称的函数，g是凸的、可微的和Lipschitz连续的且其Lipschitz常数为｜g｜，Ω⊆Rn是闭凸集。如果Φ（x，y）对任意的x∈Ω关于变量y∈Ω是凸的且可微的，▽yΦ和JgT是Lipschitz连续的且Lipschitz常数分别是｜▽yΦ｜和则在条件下，具有控制过程的微分方程系统（4）的解x（t）的轨迹的聚点就是具有约束条件的均衡规划问题（1）的解。

证明 在（5）中令y＝x＊∈Ω＊，在（7）中令y＝x＋分别可得

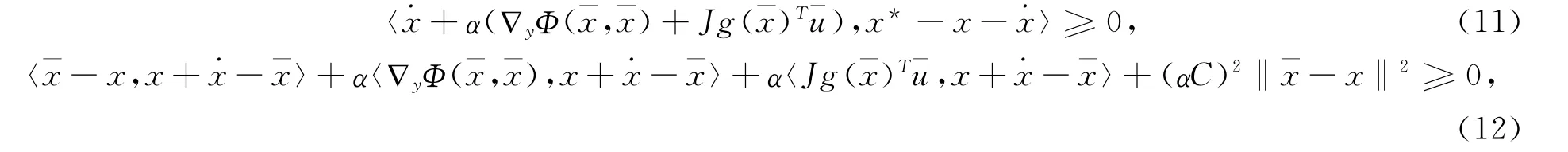
其中，C＝｜∇yΦ｜＋C0｜Jg｜。将式（11）和式（12）相加，再由函数g是凸的可得

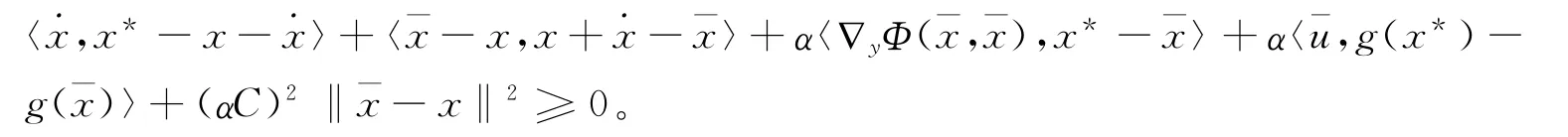
在不等式（10）中令y＝并与上式相加得

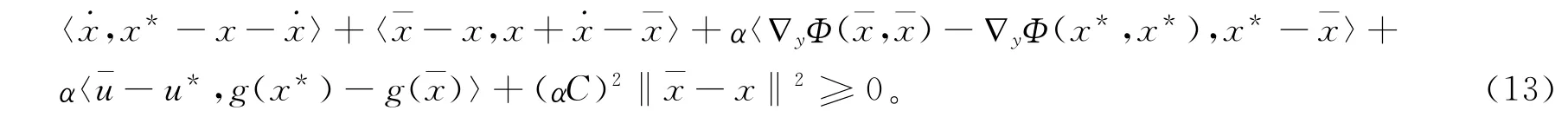
在式（6）中令v＝u＊，在（8）中令v＝u＋˙u可分别得

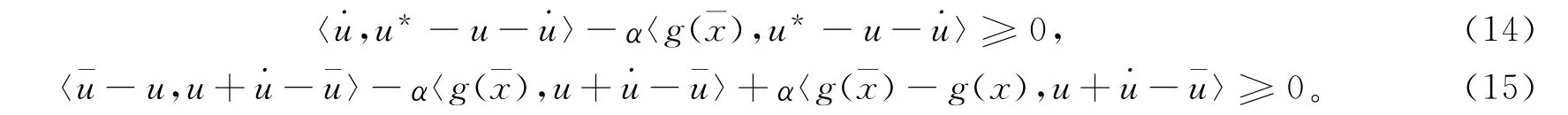
将式（14）和式（15）相加，同时应用式（9）有

由于〈ˉu，g（x＊）〉≤0和〈u＊，g（x＊）〉＝0，可将上式转化为

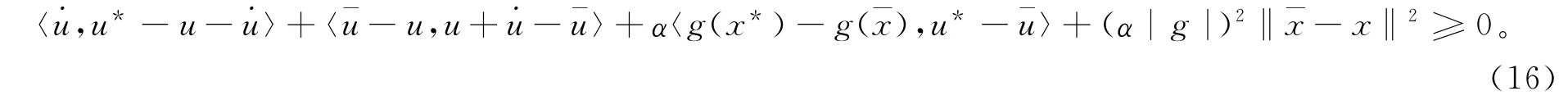
将式（13）与式（16）相加并结合性质1简化计算得

则存在t的子列｛ti｝使得当i→∞时有（ti）‖→0。由于x（t）与y（t）都是有界的，则x（ti）与u（ti）也都是有界的，从而存在｛ti｝的子列｝使得存在x′和u′有当j→∞时以及成立。在（7）中取子列｛tij｝时该式仍成立，则令j→∞可得

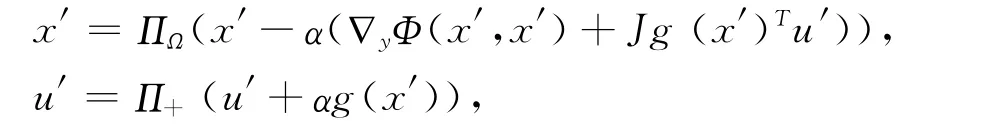
其与式（3）一致，即x′∈。证毕。

2 数值实验

运用具有控制过程的微分方程系统（4）求解2个算例，并在每个算例中描绘了微分方程系统的解的轨迹图。

例1 考虑下面的具有约束条件的均衡规划问题

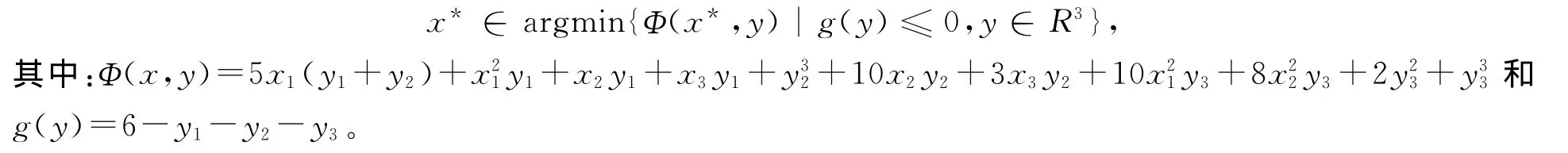
该问题的解为x＊＝（4.5，1.5，0）T。

图1为例1的微分方程系统（4）的解的轨迹图。

在本实验中，选取的参数α＝0.05。图1描绘了例1的具有约束条件的均衡问题的微分方程系统（7）的解x（t）和u（t）从五个随机产生的初始点的轨迹随时间的变化关系图。

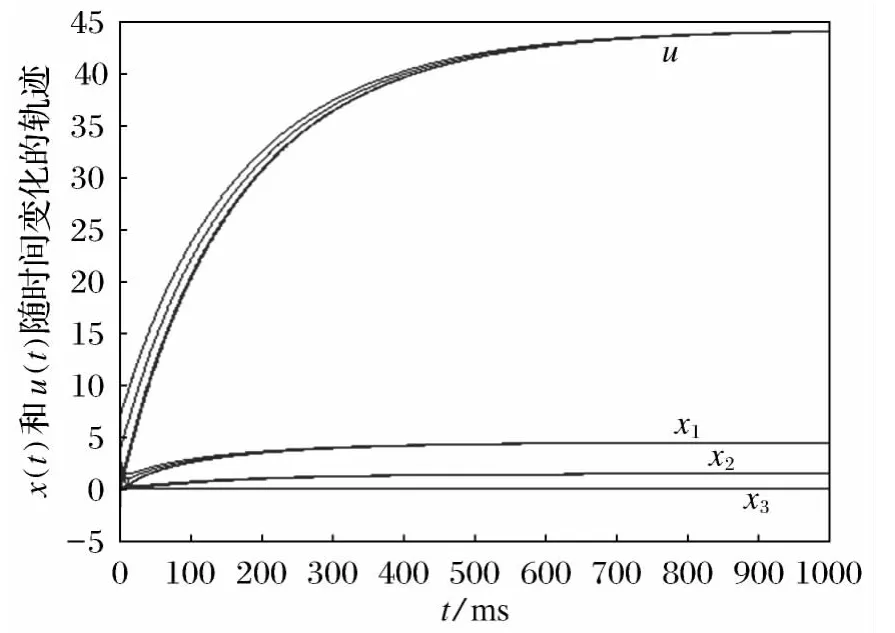
图1 例1的微分方程系统（4）的解的轨迹图

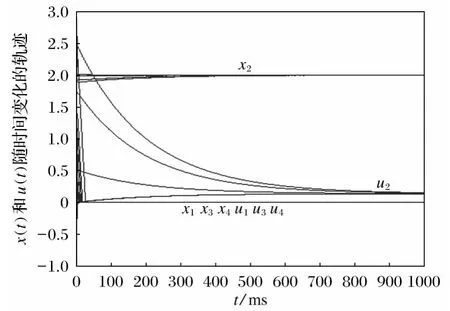
图2 例2的微分方程系统（4）的解的轨迹图

例2 考虑下面的具有约束条件的均衡规划问题

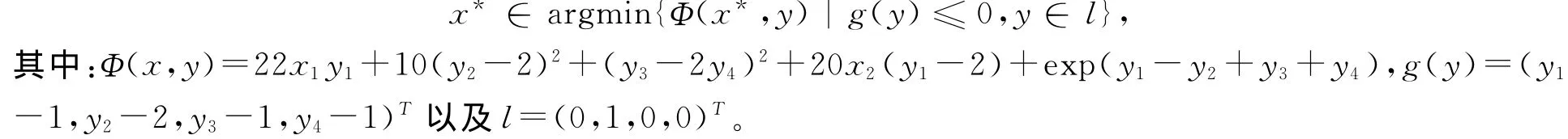
该问题的解为x＊＝（0，2，0，0）T。

在本实验中，选取的参数α＝0.1。图2描绘了例2的具有约束条件的均衡问题的微分方程系统（4）的解x（t）和u（t）从6个随机产生的初始点的轨迹随时间的变化关系图。

3 结 论

本文建立了具有控制过程的微分方程系统求解了具有约束条件的均衡规划问题，证明了该微分方程系统的解的聚点是具有约束条件的均衡规划问题的解。运用具有控制过程的微分方程系统求解了2个具体的具有约束条件的均衡规划问题，并且针对每个问题都描绘了微分方程系统的解随时间变化的轨迹图，从图中可以看出由均衡规划问题得到的具有控制过程的微分方程系统（4）的解收敛于均衡规划问题的解，从而说明了微分方程方法求解均衡规划问题的可行性。

［1］AUBEN G P，EKELAND I.Applied nonlinear analysis［M］.New York：John Wiley ＆Sons，Inc，1984.

［2］NIKAIDO H，ISODA K.Note on noncooperative convex games［J］.Pacific J Math，1955，5（1）：807－815.

［3］VENETS V I.A continuous algorithm for searching the saddle points of convex－concave functions［J］.Avtomat Telemekh，1984，45（1）：42－47.

［4］ANTIPIN A S.Evolving systems equilibrium programming：gradient methods［J］.Automation and Remote Control，1997，58（8）：1337－1347.

［5］ANTIPIN A S.Inverse optimization problem：its formulation and solution approaches［M］.Moscow：Comupting Center，Russian Academy of Sciences，1992.

［6］赵新斌，单晓成.矩阵秩优化问题的一种分离算法［J］.沈阳师范大学学报：自然科学版，2012，30（4）：454－458.

［7］ARROW K J，HURWICZ L.Reduction of constrained maxima to saddle point problems［C］∥Proceedings of the 3rd Berkeley Symposium on Mathematical Statistics and Probability，Berkeley：University of California Press，1956：1－26.

［8］FIACCO A V，MCCORMICK G P.Nonlinear programming：sequential unconstrained minimization techniques［M］.New York：John Wiely，1968.

［9］EVTUSHENKO Y G.Two numerical methods of solving nonlinear programming problems［J］.Sov Math Dokl，1974，15（2）：420－423.

［10］FRIESZ T L，BERNSTEIN D H，MEHTA N J.Day－to－day dynamic network disequilibria and idealized traveler information systems［J］.Operations Research，1994，42（2）：1120－1136.

［11］LI Yang，ZHANG Liwei.A differential equation method for solving box constrained variational ineauality problems［J］.J Ind Manag，2011，7（1）：183－198.

［12］JIN Li，ZHANG Liwei.Two differential equation systems for equality constrained optimization［J］.Appl Math Comput，2007，190（2）：1020－1039.

［13］JIN Li，ZHANG Liwei.Two differential equation systems for inequality constrained optimization［J］.Appl Math Comput，2007，188（2）：1334－1343.

［14］ANTIPIN A S.Differential equations for equilibrium problems with coupled constraints［J］.Nonlinear Analysis，2001，47（4）：1833－1844.

［15］ANTIPIN A S.The fixed points of extremal maps：computation by gradient methods［J］.Zh Vychisl Mat Fiz，1997，37（1）：42－53.