双参数C半群的Laplace变换的反演

赵华新，徐 敏，赵 拓

（延安大学 数学与计算机科学学院，陕西 延安 716000）

0 引 言

随着对半群理论的深入探讨，文献［1－3］给出了单参数C半群的若干性质及应用，文献［4］给出了广义C半群的生成元和性质，文献［5－6］研究了积分C半群、n次积分C半群的表示定理，文献［7］给出了双参数算子半群的定义及其一些基本性质，Pazy A［8］系统的研究了C0半群的性质及应用。刘春景等人在文献［9］中结合α次积分半群的Laplace逆变换的性质，导出指数有界α次积分半群的Laplace逆变换的形式，讨论了C半群的Laplace逆变换的形式，并根据n次积分C半群与C半群的关系进而得到了n次积分C半群的Laplace逆变换的形式。蔡亮等人在文献［10］中将单参数C0半群预解式的一些性质推广到了双参数C0半群上。文献［11］给出了双参数C半群及其无穷小生成元的相关性质及Hill－Yosida定理。本文基于以上的研究，给出了双参数C半群的Laplace变换的反演。

本文中X是Banach空间，所有算子都是线性算子，B（X）表示X上的有界线性算子全体，I∈B（X）为恒等算子，C∈B（X）为单射算子。

1 概念与引理

定义1［12］设C为X上的有界单射算子，若X上的算子族｛S（s，t）｝s，t≥0⊂B（X）满足

1）S（0，0）＝C；

2）CS（（s1，t1）＋（s2，t2））＝S（s1，t1）S（s2，t2），s1，t1，s2，t2≥0；

3）映射 （s，t）→S（s，t）x强连续，对∀s，t≥0，∀x∈X；

4）∃Μ≥0，α，β∈R，使得‖S（s，t）‖≤，s，t≥0。

则称｛S（s，t）｝s，t≥0为双参数强连续C半群，简称双参数C半群。

定义2［13］双参数C半群的无穷小生成元是线性变换L：R×R→B（X），其定义为：

其中，A1，A2分别是单参数C半群｛S（s，0）｝s≥0和｛S（0，t）｝t≥0的无穷小生成元，即

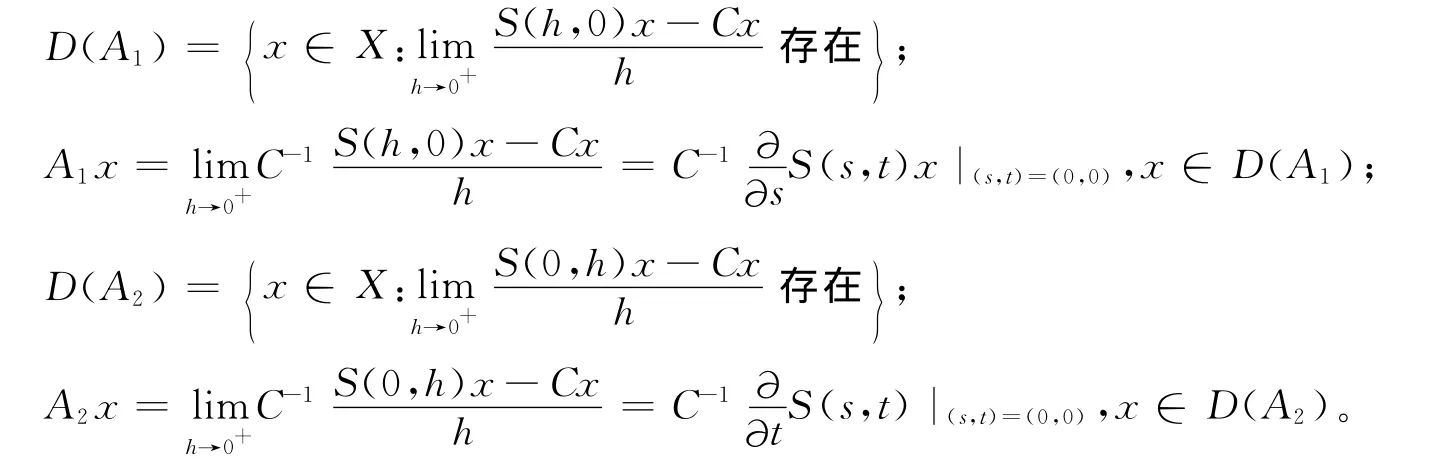
很容易得到A1，A2分别是单参数C半群S（s，0）s≥0和S（0，t）t≥0的无穷小生成元。

引理1［14］设A是满足‖T（t）‖≤Meωt的C半群｛T（t）｝t≥0的无穷小生成元。又设μ是实数，μ＞ω≥0和Aμ＝μAR（μ，A）＝μ2R（μ，A）－μI是A的Yosida逼近，则对于有

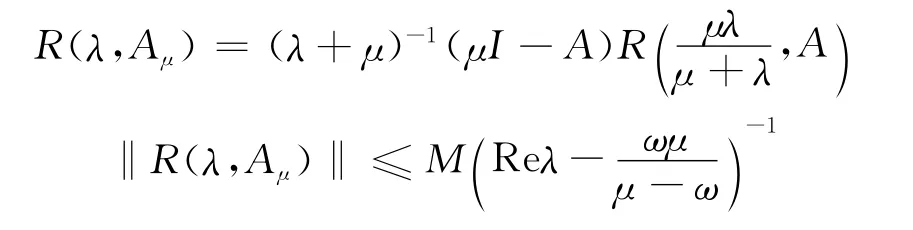
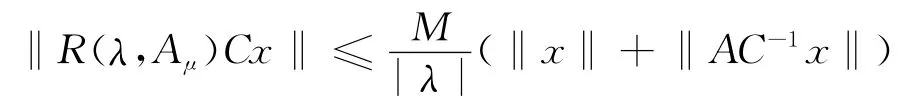
引理2［14］设A是满足‖T（t）‖≤Meωt的C半群｛T（t）｝t≥0的无穷小生成元。λ＝γ＋iη，γ是固定的，则对一切x∈X，有R（λ，Aμ）Cx＝R（λ，A）Cx，并且对∀y＞0，极限关于｜η｜≤y是一致的。

引理3［15］设A是满足‖T（t）‖≤Meωt的C半群｛T（t）｝t≥0的无穷小生成元。则对∀x∈X，λ∈ρC（A）有

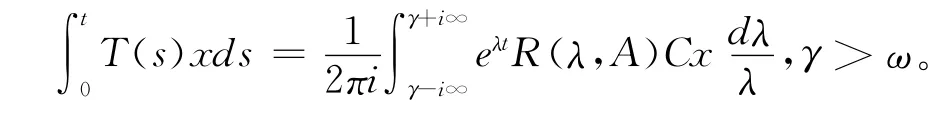
2 主要结论

定理1 设B＝（B1，B2）是有界线性算子，如果r＞‖Bi‖，（i＝1，2），那么

中的收敛是依一致算子拓扑的，并且在s，t的有界区间上是一致的。

证明 设γ＞‖Bi‖，（i＝1，2）。取r使得γ＞r＞‖Bi‖，有

并在Cr上逐项积分得

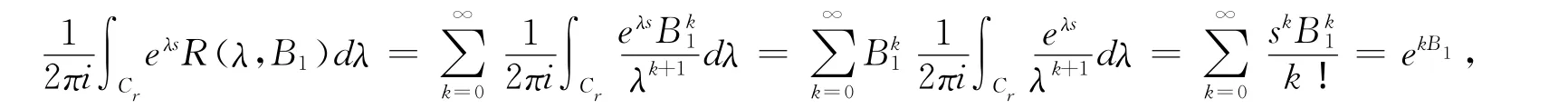
又因为上式在Cr的外部解析且

所以由Cauchy积分定理可得积分路径由Cr移动到Rez＝r上，从而

定理证毕。

定理2 设A＝（A1，A2）是双参数C半群｛S（s，t）｝s，t≥0的无穷小生成元，满足‖S（s，t）‖≤，且γ＞max｛0，ω1，ω2｝，如果x∈D（A1）∩D（A2）和C2＝C，那么

并且右端的积分在t的有界区间上关于t一致收敛。

证明 设有固定值得θ1，θ2＞0，且令

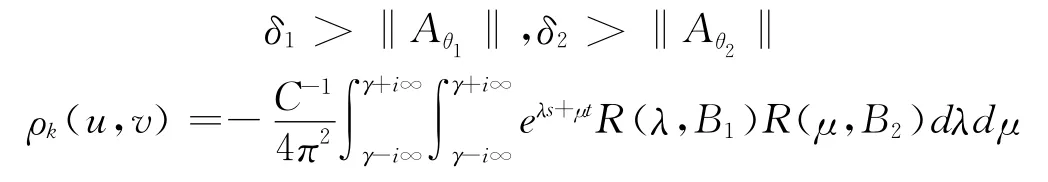
两边同时进行累次积分得

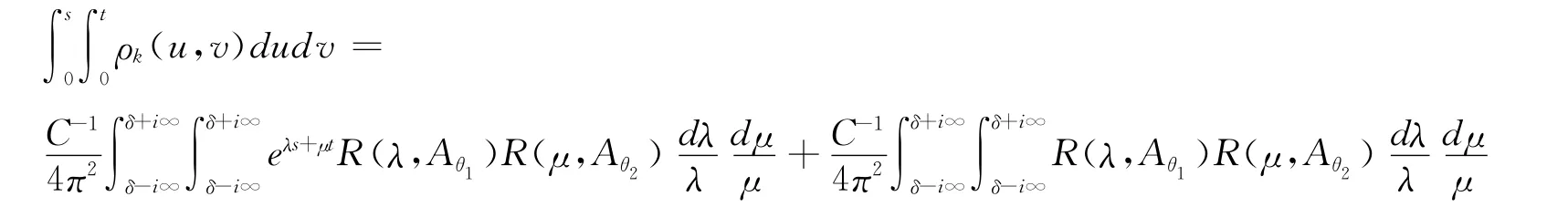
令k→∞，由引理1得

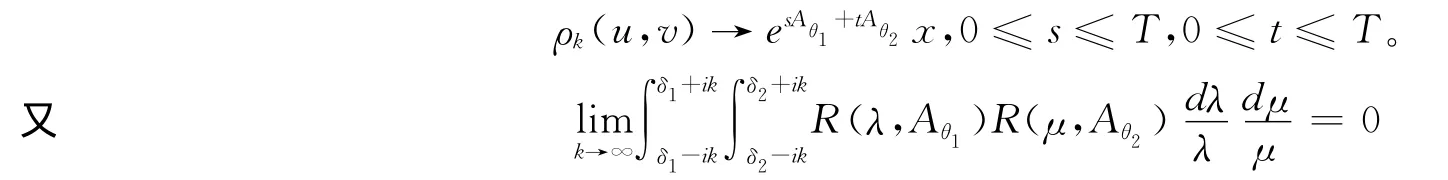
这能够通过λ－1R（λ，Aθi）x，（i＝1，2）在路径Γk上的积分推出，这里Γk由和半圆组成，当k→∞时，

对于｜λ｜≥δ成立知沿着的积分趋于0。

所以得

如果γ＞max｛ω，0｝，由引理2显然存在φ≥0，φ≥0使得θ1≥φ，θ2≥φ，｛λ：Reλ≥γ｝⊂ρ（），｛μ：Reμ≥γ｝⊂ρ（Aθ2）和x∈D（A）

由此，可以将积分路径从Reλ＝δ移到Reμ＝γ得

由引理3和式（2）得

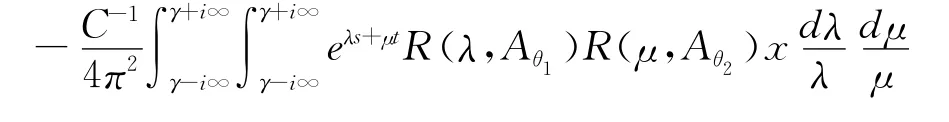
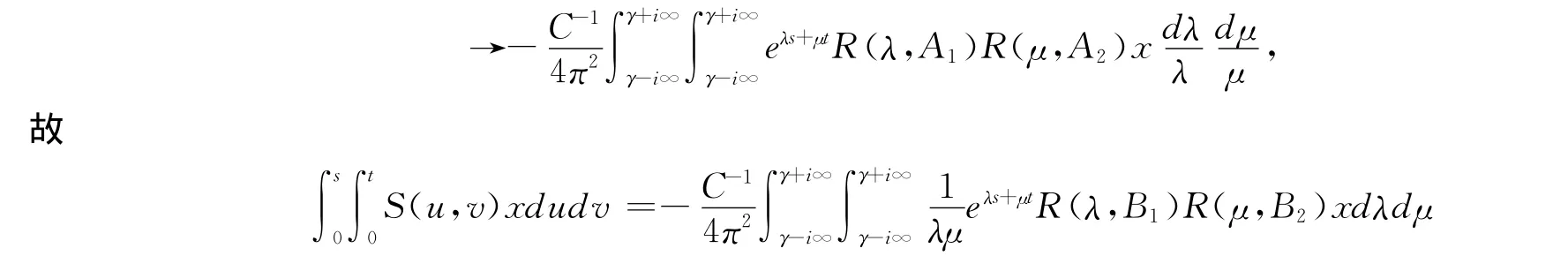
定理证毕。

3 结 语

本文以单参数C半群生成定理的Laplace刻画为基础，结合双参数C半群的指数公式，推导出双参数C半群的两种Laplace逆变换的形式。这些理论使得算子半群的内容更加丰富。

［1］王如海.C半群生成元的若干性质及应用［J］.南昌大学学报：理科版，1998，22（4）：375－379.

［2］杜厚维，李为.C半群的一些性质［J］.成都大学学报：自然科学版，2011，30（1）：29－30.

［3］贾云峰，曹怀信.无穷小生成元对指数有界C半群的刻画［J］.甘肃工业大学学报，2003，29（2）：121－123.

［4］高峰，赵华新.广义C半群的生成元和性质［J］.沈阳师范大学学报：自然科学版，2012，30（2）：137－140.

［5］胡占荣，郭春梅.Yosida逼近的应用［J］.华北工学院学报，2004，25（6）：416－418.

［6］胡敏，宋晓秋，魏巍，等.n次积分C半群的表示定理［J］.山东科技大学学报：自然科学版，2004，23（4）：89－91.

［7］SHARIF A S，KHALIL R.On the generator of two parameter semi－groups［J］.Appl Math Comput，2004，156（2）：403－414.

［8］PAZY A.Semi－groups of linear operators and applications to partial differential equations［M］.New York：Springer－Verlag，1983.

［9］刘春景，宋晓秋.α次积分半群的Laplace逆变换［J］.云南民族大学学报：自然科学版，2011，20（3）：190－195.

［10］荣嵘.积分C半群的Laplace逆变换［J］.徐州工程学院学报：自然科学版，2007，22（8）：9－11.

［11］徐敏，赵华新，赵拓.双参数C半群的一些结果［J］.沈阳师范大学学报：自然科学版，2013，31（3）：373－376.

［12］许强.关于双参数C半群的一些结果［J］.河南科学，2012，30（11）：1564－1565.

［13］徐敏，赵华新，赵拓.双参数C半群的生成元及其性质［J］.河南科学，2013，31（8）：1－4.

［14］施德明，杨录山.指数有界C半群的Laplace逆变换［J］.郑州大学学报：自然科学版，1994，26（2）：1－8.

［15］荣嵘.指数有界C半群的逼近问题［J］.南京大学学报：数学半年刊，2011，28（2）：211－219.