三维欧氏空间中的达布曲线

于延华，杨 云，刘会立

（东北大学 理学院，沈阳 110004）

0 引 言

曲线的达布向量和曲线的从切平面对于研究空间曲线的性质有很重要的作用，在实际运用中，特别在物理学、运动学上曲线的达布向量和曲线的从切平面一直为人们所关注［1］。在微分几何中，特别是空间曲线的理论中，达布向量是空间曲线Frenet标架的局部速度向量，是由Gaston Darboux发现并根据他来命名的［2－3］。因为达布向量与角动量有直接的关系，所以它也叫做角动量向量。假如一个物体沿着一个正则曲线移动，运用空间曲线的Frenet标架，物体的运动可以用2个向量进行描述：转换平移向量和旋转向量，旋转向量也就是达布向量。这种旋转是运动学上的概念，而不是物理学上的概念，因为物体在空间中自由运动时它的旋转和它的转换平移是相互独立的［4］。达布向量为解释曲率和挠率提供了一种简洁的方式：曲率是达布向量沿单位副法向量的变化量，挠率是达布向量沿单位切向量的变化量。

在微分几何中，贝特朗曲线及其侣线，曼哈姆曲线及其侣线已得到广泛研究。本文研究新的一类曲线—— 达布曲线和达布侣线［5－8］。

1 预备知识

在欧氏空间中，用〈x，y〉表示向量x＝（x1，x2，x3）和y＝（y1，y2，y3）的外积。假设r：I→R3是一条曲线且r′≠0，其中用表示向量x的长度（或称为模）。曲线r的弧长参数s由公式决定。

规定α（s）＝˙r（s），并称α（s）为曲线r在s处的单位切向量。曲线r的曲率定义为如果κ（s）≠0，则曲线r在s处的单位主法向量β（s）定义为单位向量γ（s）＝α（s）×β（s）称为曲线r（s）在s处的单位副法向量。

则Frenet－Serret公式

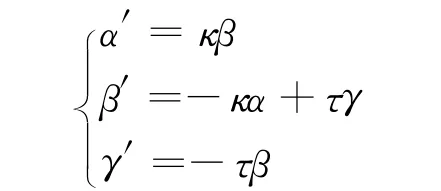
式中，τ（s）＝〈β′（s），γ（s）〉称为曲线r在s处的挠率［9］。

包含向量｛α，β｝的平面称为密切平面，包含向量｛α，γ｝的平面称为从切平面，包含向量｛β，γ｝的平面称为法平面［10］。

对任何单位速度曲线r：I→R3，称向量D（s）＝τ（s）α（s）＋κ（s）γ（s）为曲线r在s处的达布向量场。对于达布向量场有以下的Frenet－Serret公式：

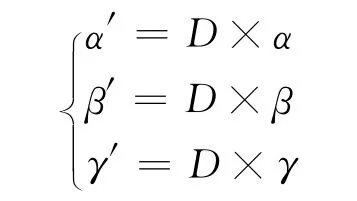
定义1 如果曲线r的切线和固定方向成定角，则曲线r称为螺旋线［12］。如果κ≠0，则曲线是螺旋线的充分必要条件是＝常数。

定义2 经过空间曲线r上的点P，且与点P的达布向量平行的直线称为曲线r在点P的达布线。

定义3 如果曲线C和的点之间建立这样的一一对应关系，使得在对应点的达布线重合，则这两条曲线都称为达布曲线。而每一条称为另一条的达布侣线。也称曲线C和为达布曲线对。在对应点达布线重合的2条曲线和r可以表达为

2 主要定理

定理1 2条曲线的主法线平行的充分必要条件是它们的达布线平行。

证明 先证必要性。

由2条曲线的主法线平行可设

从而式（1）两边同时对参数s求导可得

由式（1）和式（2）得

即

再证充分性。

根据等式（4）两边同时对参数s求导可得

由式（4）和式（5）得

由2条曲线的达布线平行可设

则式（7）两边同时对参数s求导可得

由式（7）和式（8）有

定理2 2条曲线的主法线平行，则它们在对应点的切向量成固定角。

证明 根据已知条件有∥β，则

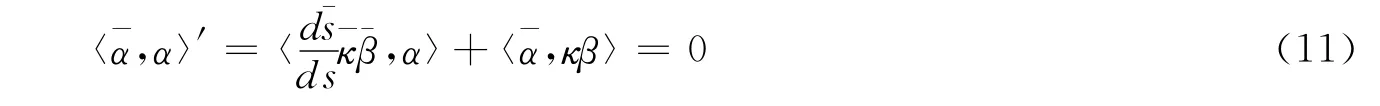
设曲线r与曲线的主法线平行，且在对应点的切向量之间的角度为θ，由定理2知，θ为常数，则两条曲线的标架有如下关系：

式中，s、α、β、γ和分别为曲线r与曲线的弧长、单位切向量、单位主法向量和单位副法向量。

这2条曲线的挠率和曲率之间的关系为：

式中，κ、τ和分别为曲线r与曲线的曲率和挠率。

由式（13）可得

结合定理2，有下列推论：

推论1 2条曲线的达布线平行，则它们在对应点的切向量成固定角。

推论2 2条曲线的主法线平行，则它们的曲率和挠率之间的关系满足公式［14］。

推论3 2条曲线的达布线平行，则它们的曲率和挠率之间的关系满足公式［14］。

推论4 2条曲线为Bertrand曲线对，则它们的曲率和挠率之间的关系满足公式［14］。

推论5 螺旋线的达布侣线仍是螺旋线。

定理3 一般螺线是达布曲线。

证明 取＝常数，设曲线r为一般螺线，考虑曲线

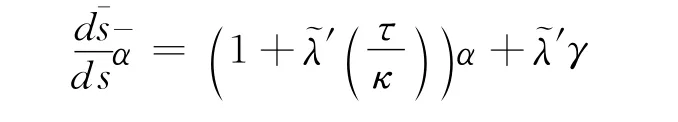
曲线（15）两边对s求导，由＝常数，则上式两边再对s求导：

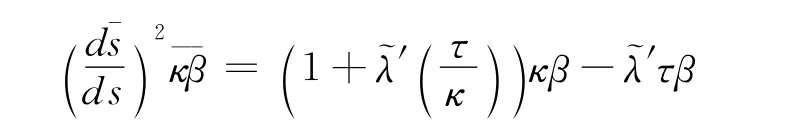
即有，由定理1得∥D，则曲线是曲线r的达布侣线。由推论5知曲线也是一般螺线。定理3证明完毕。

定理4 2条曲线为达布曲线对的充分必要条件是在对应点它们的从切平面重合。

证明 先证必要性。设曲线和r为达布曲线对，则有如下表达式：

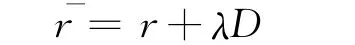
由于曲线和r为达布曲线对，则，由定理1得.另一方面，根据，可得：＝0，从而曲线和曲线r在对应点的从切平面重合。

再证充分性。

假设曲线和曲线r具有相同的从切平面，不失一般性，可设

式（16）两边分别对s进行微分，可以得到

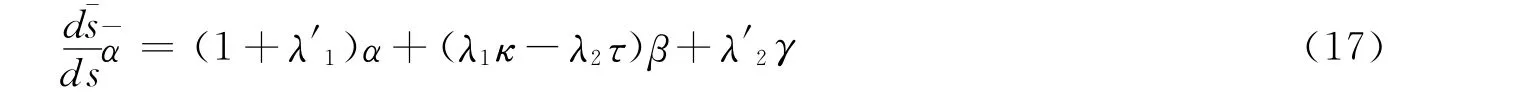
因为曲线和曲线r在相应点的从切平面重合，可以得到。

根据和定理1得，结合式（18）可知，曲线ˉr的达布线与曲线r在对应点的达布线重合。则定理4证明完毕。

如果曲线r是一条达布曲线，ˉr＝r＋λD是它的一条达布侣线，则有

结合式（12），可以得到

其中，θ为常数且θ∈［0，π］。

定理5 一条空间曲线r（s）是达布曲线的充要条件是存在函数λ（s），使得这条曲线r（s）的曲率κ（s）和挠率τ（s）满足其中θ为常数且θ∈［0，π］。

证明 必要性已证，现证充分性即证明曲线

是曲线r的一条达布侣线。

1）如果θ＝0或π，则（λκ）′＝0，等式（20）两边对s求导数，得

等式（21）再次对s求导数，得

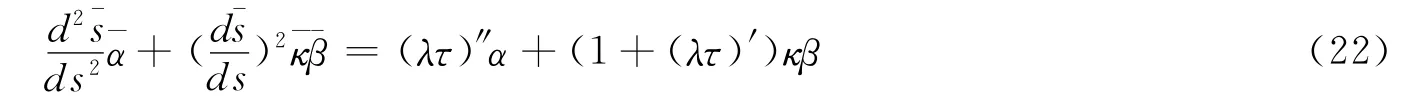
等式（20）两边对s求导数，得

再次对s求导数，得

结合式（23）、式（24）和式（25），则有由定理1得则定理5证明完毕。

推论6 2条曲线和r为达布曲线对，即如果

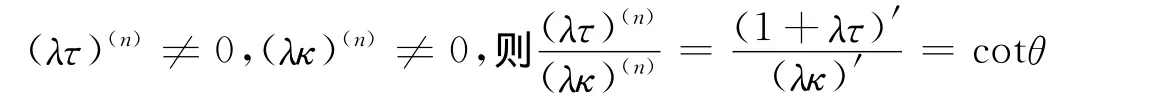
其中n＝2，3，…。

证明 根据定理5和式（19），运用数学归纳法可以得到结论。

定理6 如果曲线r的达布侣线是曼哈姆曲线，则曲线r的曲率κ和挠率τ满足以下关系：

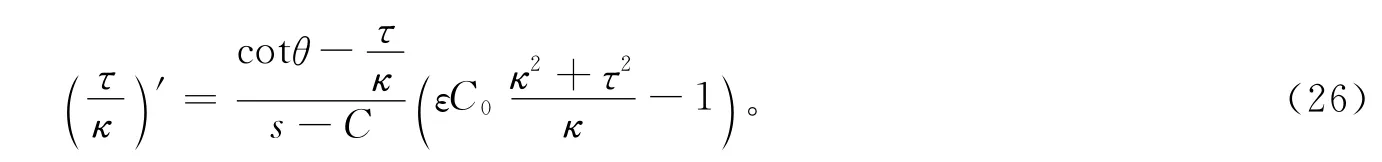
其中C，C0，θ为常数。

证明 解微分方程（19）式，可得

其中C和θ为常数。根据式（13）有

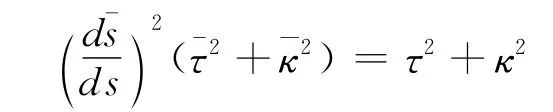
若曲线是曼哈姆曲线，则有常数结合式（19）和式（27），定理6可得证。

定理7 如果2条曼哈姆曲线是达布曲线对，则每条曲线的曲率κ和挠率τ满足以下关系：

其中，C，和θ为常数。求导数消去常数，则定理7证明完毕。

3 结 论

主要讨论了三维欧氏空间的达布曲线、2条曲线的主法线平行的充分必要条件是它们的达布线平行。在三维欧氏空间中，位置向量一直位于从切平面上的曲线称为从切曲线。根据达布向量的表达式，达布向量一直位于从切平面上。这样，位置向量是达布向量的曲线就是特殊的从切曲线。本文得到曲线的达布向量和从切平面具有这样的等价关系：两条曲线为达布曲线对的充分必要条件是在对应点它们的从切平面重合。

［1］DOCARMO M P.Differential Geometry of Curves and Surfaces［M］.New Jerse：Prentice－Hall，1976.

［2］CHEN B Y.When does the position vector of a space curve always lie in its rectifying plane？［J］.Amer Math Monthly，2003，22（10）：147－152.

［3］AHMAD A S.Maximal functions associated to surfaces of revolution on product domains［J］.J Math Anal Appl，2009，351（1）：43－56.

［4］MATTHIAS B，LARS S.On timelike willmore surfaces in Minkowski spaces［J］.J Geom Phys，2011，61（10）：1985－1995.

［5］KENMOTSU K.Surfaces of revolution with periodic mean curvature［J］.J Tohoku Math，2002，40（3）：1－11.

［6］KENMOTSU K.Surfaces of revolution with perscribed mean curvature［J］.J Tohoku Math，1980，32（1）：147－153.

［7］KIM Y H，YOUN D W.Classification of ruled surfaces in Minkowski 3－space［J］.J Geom Phys，2004，49（1）：89－100.

［8］LIU Huili.Curves in the light cone［J］.Contrib Alge Geom，2004，45（1）：225－251.

［9］YU Yanhua，YANG Yun，LIU Huiki.Centroaffine ruled surfaces inR3［J］.J Math Anal Appl，2010，365（2）：683－693.

［10］OLVER P J.Differential invariants of surfaces［J］.J Differ Geom Appl，2009，27（10）：230－239.

［11］JUN－ICHI I，SUNGWOOK L.Null curves in Minkowski 3－space［J］.Int Elec J Geom，2008，24（2）：40－83.

［12］CHEN B Y.Black holes，marginally trapped surfaces and quasi－minimal surfaces［J］.Tamk J Math，2009，32（4）：313－341.

［13］JIN H C，TAE H K，YOUNG H K.Bertrand curves in 3－dimensional space forms［J］.Appl Math Comput，2012，219（3）：1040－1046.

［14］孟旭东，易福侠.关于等价度量的若干等价判定及应用［J］.沈阳师范大学学报：自然科学版，2012，30（2）：149－152。

［15］PASCUAL L，JOSÉA O Y.Bertrand curves in the three－dimensional sphere［J］.J Geom Phys，2012，62（5）：1903－1914.

［16］BALGETIR H，BEKTASM，Null Bertrand curves in Minkowski 3－space and their characterizations［J］.Note di Mate，2004，23（4）：7－13.

［17］杨云，于延华，刘会立.三维MMinkowski空间中给定平均曲率的旋转曲面［J］.东北大学学报：自然科学版，2012，33（9）：1361－1363.

［18］于延华，刘会立.三维空间中的伪球面曲线［J］.东北大学学报：自然科学版，2007，28（4）：902－904.

［19］YU Yanhua，LIU Huili.Curves in 2－Affine Space and Eulidean Space［C］∥2007International Joint Seminar of the KOSEF－NSFC Scientific Cooperation Program，Taegu，Korea，2007：73－76.