信号控制交叉口左转相位协调设计方法

吴 伟，马万经，杨晓光

（同济大学 道路与交通工程教育部重点实验室，上海 201804）

平面交叉口设置左转相位将大幅提高交叉口各交通流间的冲突数，降低干道车流的平顺性及通行能力.因此，为了缓解交通阻塞，降低由于较大的交通需求带来的排队溢出风险，禁左已广泛应用于大城市的干道信号控制交叉口.禁左主要带来如下效益：降低绿灯损失时间，提高通行能力；干道的直行交通流通常流量很大，通过禁左能获得更多的排队空间；干道交通流的平顺性与安全性得到提升.

禁左后的左转交通流的处理方式主要有U-turns［1-2］， jughandles［3］， superstreets［4］， split intersection，quadrant roadways和 bowties［5］.这些方式都能在一定程度上解决禁左后左转交通流的处理问题，但这些方法都需要左转交通流进行绕行，提高网络总需求，并且需要改造道路，需要更多的道路空间以完成绕行，因此这些方式在很多情况下并不适用.

在信号控制方面，信号配时方案经过多年的发展，已经广泛应用于城市道路交通控制中［6-10］.现有的信号配时优化模型主要包括基于数学规划的模型和基于仿真的模型［11］.但不论何种模型，其在优化过程中都将交叉口的相位个数，如交叉口是否存在禁左或左转保护相位作为优化前给定的已知条件.但是，是否禁左、是否左转保护带来的相位个数的变化对交叉口的通行能力以及相邻交叉口间通行能力差值的影响并未详细讨论，而且相位数的变化将带来交叉口间交通流的重新分布.

基于上述分析，本文提出以交叉口间的通行能力匹配为目标，建立独立左转相位（左转保护或禁左）与信号配时整合求解的组合优化模型，能有效降低相邻交叉口相关交通流的通行能力差值.该模型的主要优势在于能为干道相邻交叉口提供最优的左转处理方式与信号配时方案.

1 问题描述

在网络交通流发生拥堵时，并不一定是网络上所有节点饱和度都过高，而更多的情况是某些关键交叉口如主路与主路交叉口需求过大，发生了过饱和，进而导致排队溢流等问题，而其他非关键交叉口如主路与支路交叉口可能仍然存在通行能力过剩.因此，本文研究在交叉口供需不平衡的情况下，利用左转协调设计匹配上下游交叉口间的通行能力，提高整个交叉口群的总体效益，降低延误，提高通行能力.

2 参数定义与说明

以两个普通交叉口为例，左转协调设计只考虑干道方向，交叉口基本布局如图1所示，模型构筑中需要的参数解释如表1所示.

表1 参数说明表Tab.1 Parameters

图1 交叉口基本布局与参数Fig.1 Intersection layout and basic notations

3 基本假设

本文模型基于以下假设：

（1）如果交叉口i进口道2，4禁左，交叉口j进口道2，4不禁左，则经由交叉口i进口道2，4左转的车流将经交叉口j进口道2，4左转，反之亦然.

（2）禁左后原左转车道转换为直行车道.

（3）进口道1，3的车流在交叉口i或交叉口j禁左后有绕行路径，交叉口i东西方向禁左后绕行路径如图2所示（实线代表原路径，虚线代表禁左后的绕行路径）.

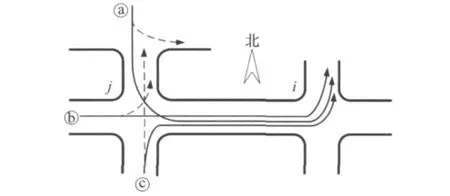
图2 交叉口i东西方向禁左后绕行路径示意图Fig.2 The routes for circumambulation when left-turn is forbidden at intersection i

4 优化模型构筑

4.1 约束条件

（1）流量守恒约束

优化前的总流量等于优化后的总流量.优化后，根据交叉口的左转组织方式（左转保护或禁左），各流向的流量对比优化前将重新分配，故应重新计算交叉口各进口道各流向的流量.

进口道1：优化前后进口道1的直行和右转流量保持不变.而优化后进口道1的左转流量随着下游交叉口进口道4是否禁左而不同，如果不禁左，则σ-A＝0，优化前后流量相等；如果禁左，则σ-A＝1，优化后的流量应减去由于禁左引起的绕行流量，如图2中绕行路径ⓐ所示.进口道1优化后流量重分布的结果表示为

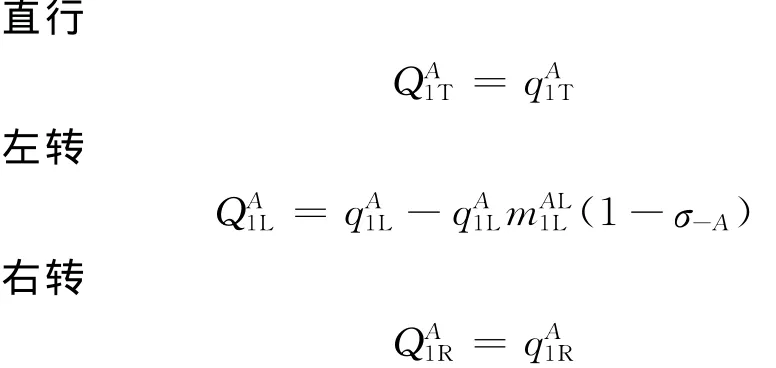
进口道2：优化前后右转流量相等，而下游交叉口是否禁左将影响直行和左转流量的大小，见图2禁左后的绕行路径ⓑ.优化后进口道2的流量表示为

进口道3：优化前后的左转流量相等，而直行和右转流量受下游交叉口是否禁左的影响，可参见图2绕行路径ⓒ.优化后的流量表示为

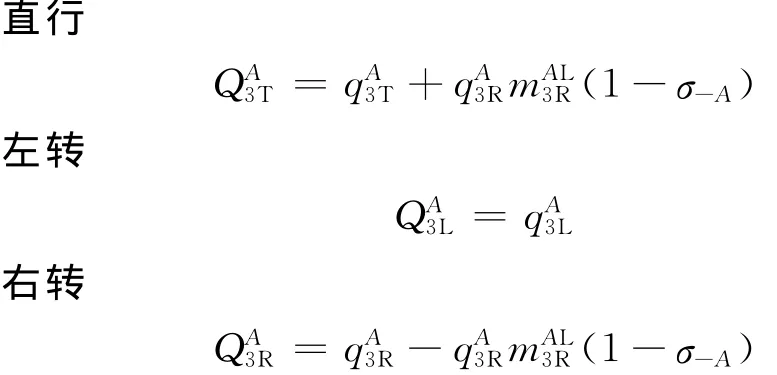
进口道4的流量根据上游交叉口其他几个进口道的流量以及每股车流的转弯比计算得出，此处不再赘述.

（2）车道数守恒约束

优化前后各交叉口进口道车道数守恒

（3）转向分配比例约束

优化前后的各流向流量转向分配比例之和为100%，即

优化后，根据下游交叉口不同的左转组织方式，上下游相关联流向即进口道2直行，进口道1左转，进口道3右转，进入下游交叉口进口道4的左、直、右转弯比例将重新分配.

进口道1：优化前后由进口道1左转流出进入下游交叉口进口道4继续直行和右转的流量保持不变，则转弯比表示为

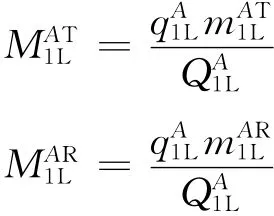
则优化后此流向的左转转弯比表示为

与进口道1的计算方法一样，进口道2与进口道3优化前后由上游交叉口流出进入下游交叉口进口道4继续直行和右转的流量保持不变，计算方法也一样，此处不再赘述.

（4）绿灯时间约束

绿灯相位持续时间应小于最大绿灯时间，大于最小绿灯时间，即

式中：g＝C0λ，按等饱和度分配绿信比，则交叉口各流向的绿信比λ为

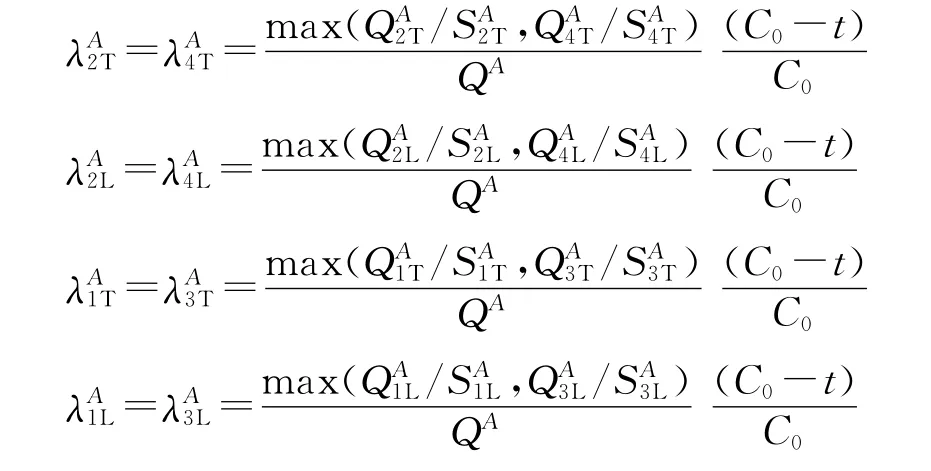
（5）信号周期约束

两个交叉口的周期应满足最小周期与最大周期的约束，为了交叉口间的协调，还要满足共同周期约束

（6）饱和度约束

优化完成后应满足各相位的饱和度小于1.

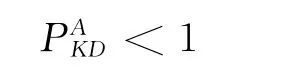
（7）左转相位设计约束

左转协调设计应满足至少有一个交叉口设置左转相位，保证左转交通流能顺利通行.

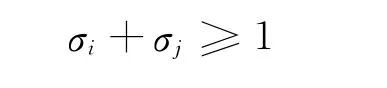
4.2 目标函数

本文的目标函数为上下游交叉口的通行能力相互匹配，由于考虑右转有专用车道且不受控，通行能力能满足需求，因此主要考虑下游左转与直行和上游流入方向的通行能力匹配.令ΔE1，ΔE2分别表示交叉口i流向交叉口j直行与左转的通行能力匹配值，匹配流向如图3所示.ΔE3，ΔE4分别表示交叉口j流向交叉口i直行与左转的通行能力匹配值.

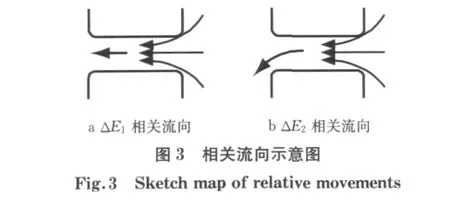
计算通行能力匹配值的方法为下游能排放出去的通行能力减去上游到达流向的通行能力，其计算公式如下式所示：

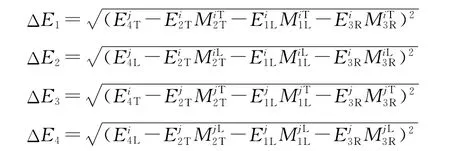
式中通行能力E的计算公式为E＝SλL，即通行能力等于单车道饱和流量、绿信比、车道数的乘积.

本文的目标函数为使最大的通行能力匹配值最小化

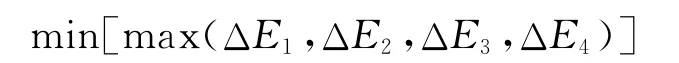
控制变量为：二元变量代表是否禁左，σi，σj；共同周期时长，C0；绿信比，λ.

5 实证分析

选择济南市纬二路主干道中的经三路交叉口与经四路交叉口为案例进行分析，其中，经三路交叉口（交叉口i）为主支相交，经四路交叉口（交叉口j）为主次相交，交叉口的设计、流量如图4所示，交叉口的间距为450m.两交叉口流入路段流量在下游的转向分配比例如表2所示，其中i，j表示交叉口，下标表示进口道（见图1）.

实证分析对比了三种方案的控制效果：

第一为原方案（未考虑通行能力匹配），交叉口i为两相位，交叉口j为四相位.

第二为本文模型优化的方案，优化完成后两个交叉口都为三相位控制.

第三为Synchro计算生成的配时方案，其方案的相位安排与原方案类似，各方案的相位设置见图4c.

应用Visul Basic软件开发工具对本文模型进行信号配时以及相位设置参数优化，并利用Synchro对三种方案进行评价分析，结果如表3，4和图5，6所示.

表2 路径流量分配比例表Tab.2 Allocation of routes volume %

表3显示了三种方案下的信号配时参数对比，与原有方案相比，Synchro方案信号周期值由160s下降到150s，而本文方案的优化信号周期值则下降到92s.而饱和度的变化进一步指出文本模型能在保证饱和度与其他方案相差不大甚至略优的情况下，利用更小的周期就能满足交通需求.

表4显示了三种方案下交叉口间的通行能力差值的对比，从表中可以看出本文模型能大幅减少交叉口之间通行能力的不匹配.

表3 信号控制方案对比表Tab.3 Comparison of results of different signal plans

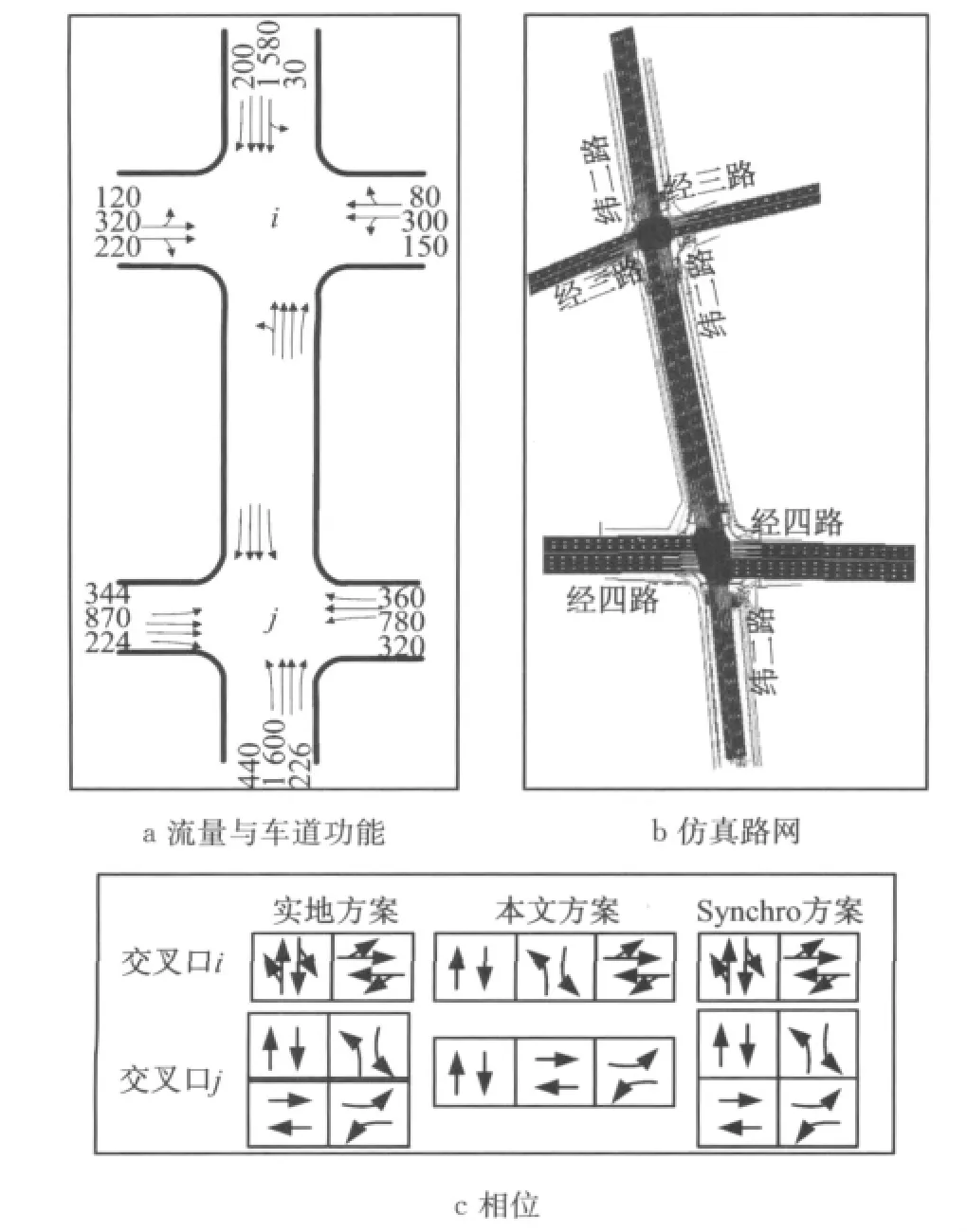
图4 实证案例的交叉口流量与相位设置Fig.4 Experimental intersection layout，traffic volume and phase settings

表4 不同信号控制方案通行能力差值对比表Tab.4 Comparison of capacity gap of different signal plans pcu·h-1

从图5可以看出，考虑通行能力匹配后的相位设置与信号配时能显著降低交叉口j车均延误，与此同时，交叉口i的车均延误也明显上升，总体上，考虑通行能力匹配后的信号配时与相位设计可降低车均延误42%，并使得交叉口i与交叉口j的车均延误相互接近，即流量在交叉口i与交叉口j的分布更加均匀.

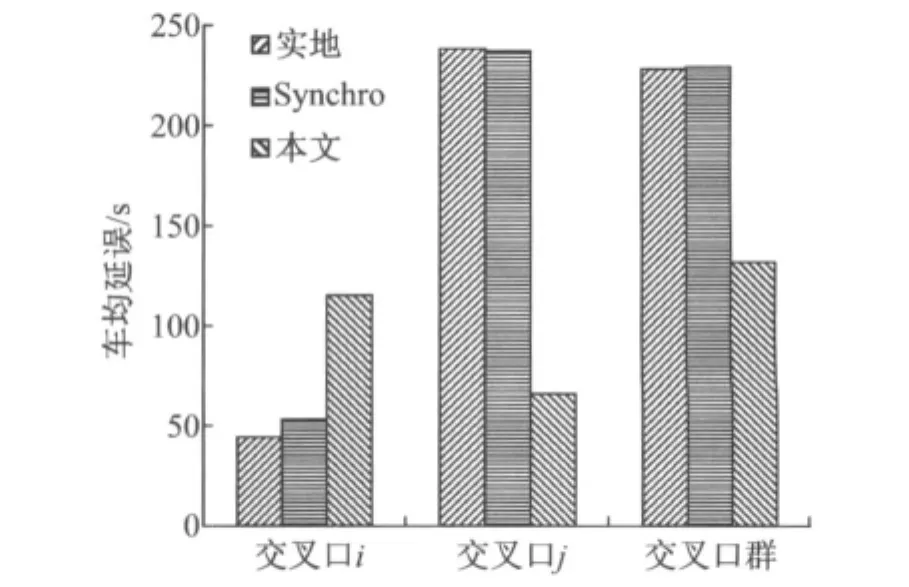
图5 车均延误对比图Fig.5 Comparisons of the average delay for different signal plans

从图6可以看出，考虑通行能力匹配后的信号配时与相位设计，即使在周期较短，绿灯时间低于长周期的情况下（92s周期对应单位小时的绿灯时间约为3248s，160s周期对应单位小时的绿灯时间约为3330s），交叉口i与交叉口j的绿灯通过车辆数相对于原方案与Synchro方案均提高，且整个网络的绿灯通过车辆数提高10%，证明本文模型能从整体角度疏解网络的瓶颈，提高网络整体的通行能力.

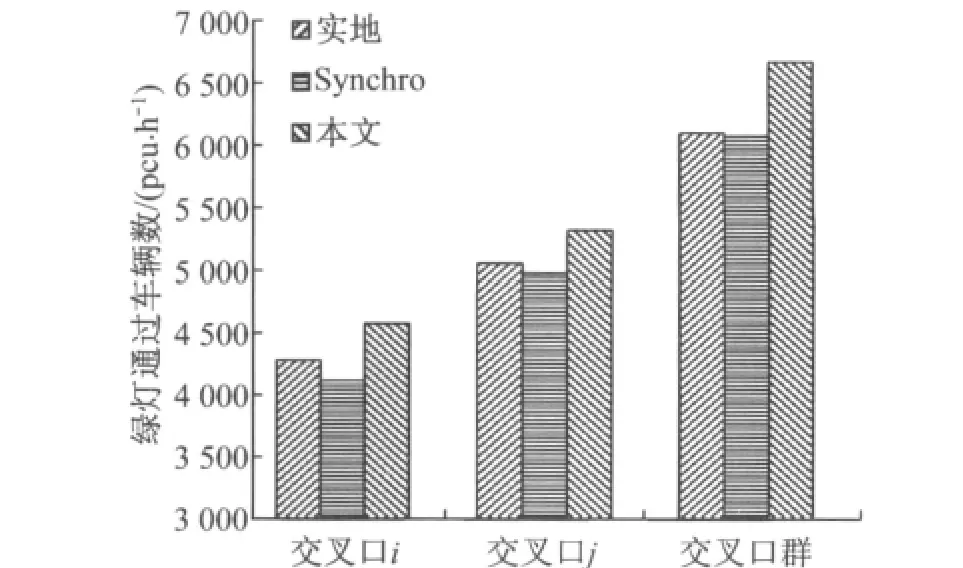
图6 绿灯通过车辆数对比图Fig.6 Comparisons of throughput for different signal plans

6 结论

交叉口群是相互关联的整体，上游交叉口的排出交通量决定着下游交叉口的需求量，追求网络中单个交叉口最优的信号配时可能会导致其下游交叉口过饱和，甚至发生拥堵.因此，考虑网络整体的效益，充分挖掘现有交通设施的潜力，将局部拥挤的交通流转移至通行能力过剩的区域是交通网络设计所应达到的效果.本文正是基于以上思路，考虑通行能力匹配，进而设计交叉口左转相位及信号配时，从交叉口群整体的角度考虑交叉口间的需求与时空资源供给平衡，研究结果表明本文模型能有效地降低交叉口群的车均延误，提高交叉口绿灯时间车辆通过数，并使车流在各交叉口间的分布更加均匀.

当交叉口群中各交叉口的需求发生变化时，本文模型在各交叉口间所能取得的效益可能会发生变化，在应用过程中，应根据不同流量水平利用本文模型进行分时段优化.同时，如果相交道路的各交叉口也考虑通行能力匹配设置左转相位与信号配时，将能获得更高的整体效益.在后续的研究中，还应该考虑左转车流绕行的问题以分析本方法的适应性，并基于网络交通均衡等思想进一步研究本文模型在更复杂网络上的拓展和应用.

［1］Pirdavani A，Brijs T，Bellemans T，et al.Travel time evaluation of a U-turn facility and its comparison with a conventional signalized intersection［C］／／90th Transportation Research Board Annual Meeting.Washington D C：TRB，2011：26-33.

［2］Esawey M，Sayed T.Operational performance analysis of unconventional median U-turn design using micro-simulation［C／CD ］／／90th Transportation Research Board Annual Meeting.Washington D C：TRB，2011.

［3］Jagannathan R，Gimbel M，Bared J，et al.Safety comparison of New Jersey jug handle intersections and conventional intersections［C］／／85th Transportation Research Board Annual Meeting.Washington D C：TRB，2006：187-200.

［4］Haley R，Ott S，Hummer J，et al.Operational effects of signalized superstreets in North Carolina ［C ］／／90th Transportation Research Board Annual Meeting.Washington D C：TRB，2011：72-89.

［5］Reid J D，Hummer J E.Travel time comparisons between seven unconventional arterial intersection designs［C］／／80th Transportation Research Board Annual Meeting.Washington D C：TRB，2001：56-66.

［6］Papageorgiou M，Diakaki C，Dinopoulou V，et al.Review of road traffic control strategies［J］.Proceedings of the IEEE，2003，91（12）：2043.

［7］Cai C，Wong C，Heydecker B.Adaptive traffic signal control using approximate dynamic programming［J］.Transportation Research Part C：Emerging Technologies，2009，17（5）：456.

［8］Royani T，Haddadnia J，Alipoor M.Traffic signal control for isolated intersections based on fuzzy neural network and genetic algorithm［C］／／89th Transportation Research Board Annual Meeting.Washington D C：TRB，2010：87-91.

［9］Singh L，Tripathi S，Arora H.Time optimization for traffic signal control using genetic algorithm［J］.International Journal of Recent Trends in Engineering，2009，2（2）：4.

［10］Smith B，Venkatanarayana R，Park H.Development of new traffic control signal algorithms under Intellidrivesm.Intellidrivesm pooled fund study report—task 2 ［R］.Charlottesville：University of Virginia，2010.

［11］LIU Yue，CHANG Ganglen.An arterial signal optimization model for intersections experiencing queue spillback and lane blockage［J］.Transportation Research Part C：Emerging Technologies，2011，19（1）：130.