干散货航运价格指数的多重分形特征分析*

李电生 李运红 万培祥

(中国海洋大学 经济学院，山东 青岛 266100)

干散货航运价格指数的多重分形特征分析*

李电生 李运红 万培祥

(中国海洋大学 经济学院，山东 青岛 266100)

运用多重分形理论对干散货航运价格指数的分布结构进行研究，对运价指数的广义Hurst指数、质量指数τ(q)进行估算，结果表明干散货航运价格指数时间序列具有多重分形特征。并且结合多重分形谱分析法对运价指数的内部结构进行了研究，发现多重分形谱图左端明显低于右端，呈密集型分布，表明国际干散货运价指数总体呈增大趋势。

运价指数；多重分形理论；多重分形谱分析法

一、引言

由波罗的海航交所发布的BDI指数是衡量国际海运情况的领先指数，能够反映各国的经济情况及国际间的贸易情况。该指数受全球铁矿、煤矿和谷物运输需求量、全球船吨数供给力、国际船用燃油平均价等多种因素的综合影响，波动频繁，给市场运营者的决策带来风险，如受欧债危机和运力过剩的影响，中国远洋在2011年亏损104.5亿元人民币后，2012年上半年再次亏损48.7亿。然而，BDI指数波动频繁并不是无规律可循，研究BDI指数的分布特征可以为市场参与者在决策上提供帮助，降低决策风险。

最初，在对运价指数分布规律的研究上，随机游走过程得到广泛应用，随后提出了有效市场理论，然而这两者都不能够很好地揭示航运市场的真实情况，随着理论研究的不断深入和分形几何理论在其他领域应用的迅速发展，在航运市场价格波动特征的研究方面，分形理论逐步引起学者的关注，已有学者开始将分形理论应用到对航运市场价格指数分布规律的研究上，证实了BDI指数具有分形特征。万九文，吕靖等，[1]李电生，万培祥等运用不同的方法证实国际干散货航运市场具有分形特征。[2]但是，随着分形几何理论的发展，学者发现，单分形只能分析数据波动形态的宏观走势，反映信号总体粗糙和复杂程度，不能完全刻画信号特征和真实市场，表明市场本身表现出的并不是单分形结构，而是更精细的多重分形结构，当单一维数不能完全描述数据的精细特征时，需要通过多重分形谱来体现信号局部的奇异性。

单分形是用一个参数来刻画时间序列在不同时间尺度上的分形特征，而多重分形试图用一些特征指数来刻画时间序列的局部分形特征，更好地描述数据的精细结构。目前，国内外学者对时间序列多重分形结构的研究已有很多。国外学者Ghashghaie等以美元/马克国际汇率为研究对象，[3]发现对汇率变化的研究需要运用多重分形理论。Skjeltorp等对挪威的股票价格指数进行标度特性研究，得出同样结论。[4]国内研究有：张永东等，何建敏等发现单分形不能够描述我国股票市场的复杂特性，中国股票市场具有多标度特征。[5-6]在时间序列多重分形结构的确认上，主要方法有q阶矩分割函数法、多仿射法、多重分形去趋势波动分析法和配分函数法等。Schmittf等运用最原始、最简单的q 阶矩分割函数法对美元/法郎的汇率进行了研究，结果表明，汇率变化是一个多重分形过程。[7]q阶矩分割函数法要求时间序列是正规的、平稳的，自身具有很大的局限性，在以后的研究中多使用后面的几种方法。Ausloos等运用多仿射法研究了德国股票市场的多重分形特征，[8]朱林、常松等对我国股票市场的多仿射现象进行分析，发现我国股票市场存在明显的多重分形结构。[9]于建玲、臧保将等借助配分函数、广义分形维数和多重分形谱对股票市场进行研究，[10]李海洋，王磊运用多重分形去趋势波动分析法(MF-DFA)，[11]均发现股票市场存在明显的多重分形特征。航运市场价格与股票市场价格波动特性具有相似的统计特征，研究内容可以借鉴，由于二者的影响因素和形成机制等的不同，需要对研究内容的真实性进行检验。

由Kantelhardt于2002年提出的多重分形去趋势波动分析法(简称MF-DFA)，可以发现非平稳时间序列中的长程相关性，该方法自成立以来，被各个领域应用于分析其多重分形特性上。Matia等使用该方法证实了多种商品和股票的日价格具有多重分形结构，[12]Norouzzaden运用MF-DFA研究汇率波动特征，发现多重分形谱对非线性相关性研究有很大贡献。[13]袁平平、于建玲等用MF-DFA法研究沃尔玛指数日收盘价的多重分形特性，[14]陈洪涛、顾荣宝等用MF-DFA法研究原油价格的多重分形特征等，[15]实证表明，MF-DFA在研究时间序列多重分形结构的问题上是可行的。

本文采用多重分形去趋势波动分析法(MF-DFA)，通过对BDI指数的广义Hurst指数、质量指数的研究，证实BDI指数时间序列具有多重分形特征，并通过多重分形谱分析方法对运价指数的多重分形结构进行了研究。

二、多重分形结构特征参数及其计算过程

(一)广义Hurst指数

多重分形去趋势波动分析法(简称MF-DFA)，是Kantelhardt等人在传统去趋势波动分析法(简称DFA)基础上于2002年提出的，该方法在研究非平稳时间序列多重分形结构问题上，能够发现序列的长程相关性，避免对序列的相关性做出不正确判断，研究结构更加可靠。广义Hurst指数是MF-DFA中最常用的特征参数，通过判断该指数H(q)与阶数q的关系来判断时间序列是否具有多重分形结构。广义Hurst指数的计算过程如下：

对于给定的长度为N的时间序列{xi}(i=1,2,…,N)，利用MF-DFA法计算广义Hurst指数，步骤如下：

求时间序列{xi}(i=1,2,…,N)对于均值的累计离差：

(1)

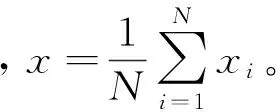
(2)

(3)

(3)对单个区间序列，采用最小二乘拟合法分别解出其拟合趋势多项式pk(l)，其中pk(l)可以是1次，2次等多项式，其表示第k,k=1,2,…,2m个小区间上的局部趋势函数。消除每一子区间的局部趋势序列，得到残差序列Ck(l)为：

当k=1,2,……，m时，

Ck(l)=y(k-1)n+l-pk(l),l=1,2,…,n；

(4)

当k=m+1,m+2,……，2m时，

Ck(l)=yN-(k-m)n+l-pk(l),l=1,2,…,n。

(5)

用F2(n,k)表示第k 段残差序列的平方均值，有：

(6)

(4)求序列的q阶波动函数。对于非零实数q,定义序列的q阶波动函数为：

(7)

当q=0时，定义序列的波动函数为：

(8)

当q=2时，MF-DFA将退化为DFA。

(5)q阶波动函数Fq(n)的主要性质是其揭示了一个分形信号幂定律的尺度关系，对于每一个固定的q，有幂律关系式Fq(n)～nh(q)。对每一个子区间长度n,可以求出对应的波动函数值Fq(n)，将上述幂律关系式取对数，推得：

logFq(n)=logC+h(q)logn,

(9)

其中，C为常数。作出logFq(n)～logn函数关系散点图，用最小二乘法做线性回归，其斜率就是q阶广义Hurst指数h(q)。

通过上述步骤得到与不同q相对应的h(q)值，当h(q)为常数，即h(q)不依赖于q时，所研究序列为单分形的；当h(q)随q增大而减小，即h(q)依赖于q且关于q为单调下降时，序列就是多重分形的。h(q)值的取值范围为0到1，通过h(q)的取值，可以判断序列的长程相关性，当h(q)位于0到0.5之间时，序列是反持续的，当h(q)等于0.5时，序列是随机时间序列，当h(q)介于0.5到1时，序列具有持续性。

(二)质量指数τ(q)确定

在上述过程中得到的广义Hurst指数h(q)与质量指数τ(q)相关，二者的关系如下：

τ(q)=qh(q)-1。

(10)

当所分析过程为多重分形时，它的尺度函数τ(q)必有如下性质：τ(q)是一个凹函数；当q=0时，所有的尺度函数具有相同的质量指数-1；τ(q)是q的非线性函数。通过尺度函数τ(q)的性质可以进一步判断时间序列是否具有多重分形结构。

(三)多重分形谱分析

现有文献对多重分形谱的解释主要有三类，实际研究表明最合适的解释要由具体研究内容来决定。本文定义多重分形谱为具有相同Hölder指数α集合的分维数。具体计算过程如下：

将时间序列{xi}(i=1,2,…,N)按时间标度ε(ε<1)等分为互不相交的N个小区间，令：

Pj(ε)=Ij(ε)/∑Ij(ε),j=1,2,…,N,

(11)

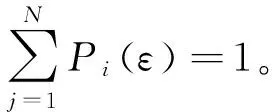
当时间序列具有多重分形特征时，有幂律关系：Pj(ε)∝εα，α表示第j个小区间的奇异指数，用α表示分形子集的分维数就是多重分形谱函数f(α)。把具有奇异指数α的子集中概率相同的区间个数记为Nα(ε)，则满足幂律关系式Nα(ε)∝ε-f(α)，对上式两边取对数，然后进行最小二乘法拟合可以得到f(α)值。计算多重分形谱同样可以从另一角度算出：

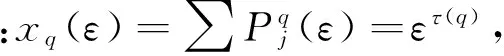
(12)

f(α)=qα(q)-τ(q)。

(13)

αmin和αmax分别表示概率最大和最小子集，Δα=αmax-αmin表示概率变化不均匀性，Δα越小，表示概率的分布范围越窄，多重分形特征越不明显；f(αmin)和f(αmax)分别表示最大和最小概率子集的单元数目，Δf=f(αmin)-f(αmax)表征最大最小概率子集出现频率的变化。

三、BDI指数多重分形结构研究

(一)干散货运价指数多重分形特征分析

1、数据选取

文章选用2001年1月2日到2012年11月30日由波罗的海航交所发布的共2972天的BDI指数为研究对象，其实际波动如图1。对运价指数进行分析时，考虑的是收益率序列，首先运用公式R(t)=logP(t+1)-logP(t)，将原序列转换为对数收益序列，其中P(t)为航运市场第t个工作日的运价指数，R(t)为航运市场日收益率，结果如图2。

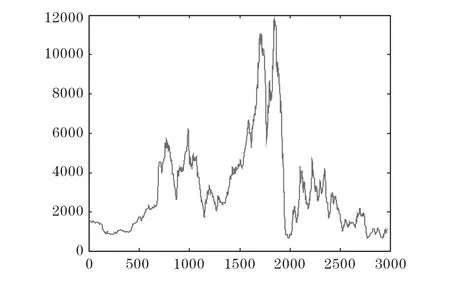
图1 BDI波动图

2、广义Hurst指数分析

文章运用MF-DFA法来研究表征运价指数收益序列多重分形性质的特征参数广义Hurst指数，用Matlab7.0对式(1)到式(9)进行编码。

图3为BDI指数对数收益序列对于均值的累积离差走势图，从图3可以看出，序列{yj}(j=1,2,…,N)在不同时间间隔内，变化趋势差异很大，上升和下降趋势的持续时间与幅度均变化不定，说明BDI指数的波动规律具有复杂性。

在进行多重分形去趋势波动分析时，q的取值范围为(0:0.5:10)。图4(上)为q取不同值时，波动函数Fq(n)和n的双对数关系图，在图4(上)中，各曲线从下到上，q值依次增大，对应的斜率h(q)逐渐变小，说明h(q)关于q是单调下降的。用最小二乘法进行拟合，得到广义Hurst指数h(q)随q变化的相应取值，如表1，其趋势图如图4(下)。

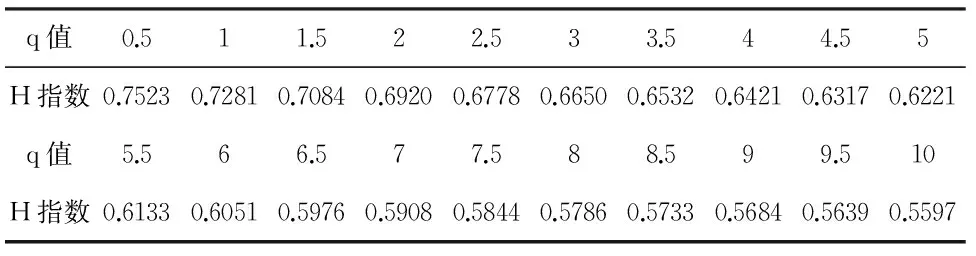
表1 BDI指数收益率序列广义Hurst指数

当q=0时，h=0.7828，q从0变化到10时，BDI收益序列的h(q)值从0.7828递减到0.5579，运价指数收益序列的h(q)值显然不能用常数来表示，说明BDI收益序列具有明显的多重分形特征，用单一分形不能对其进行充分描述。从表1中看到，运价指数收益序列的广义Hurst指数h(q)都介于0.5到1之间，说明运价指数时间序列具有持续性，即若运价指数在前一阶段具有上升(下降)趋势，在下一阶段走势中，运价指数在很大程度上会继续保持上升(下降)趋势。从图4(下)可以看出，h(q)关于q单调下降，说明BDI收益序列具有多重分形结构。

3、质量指数τ(q)

图5为以阶数q为横坐标，以运价指数收益序列的质量指数τ(q)为纵坐标的q-τ(q)关系图，从图上可以看出τ(q)是一个凹向横轴的函数，当q=0时，τ(q)=0，τ(q)是关于q 的非线性函数，由以上性质，进一步证明运价指数时间序列具有多重分形结构。

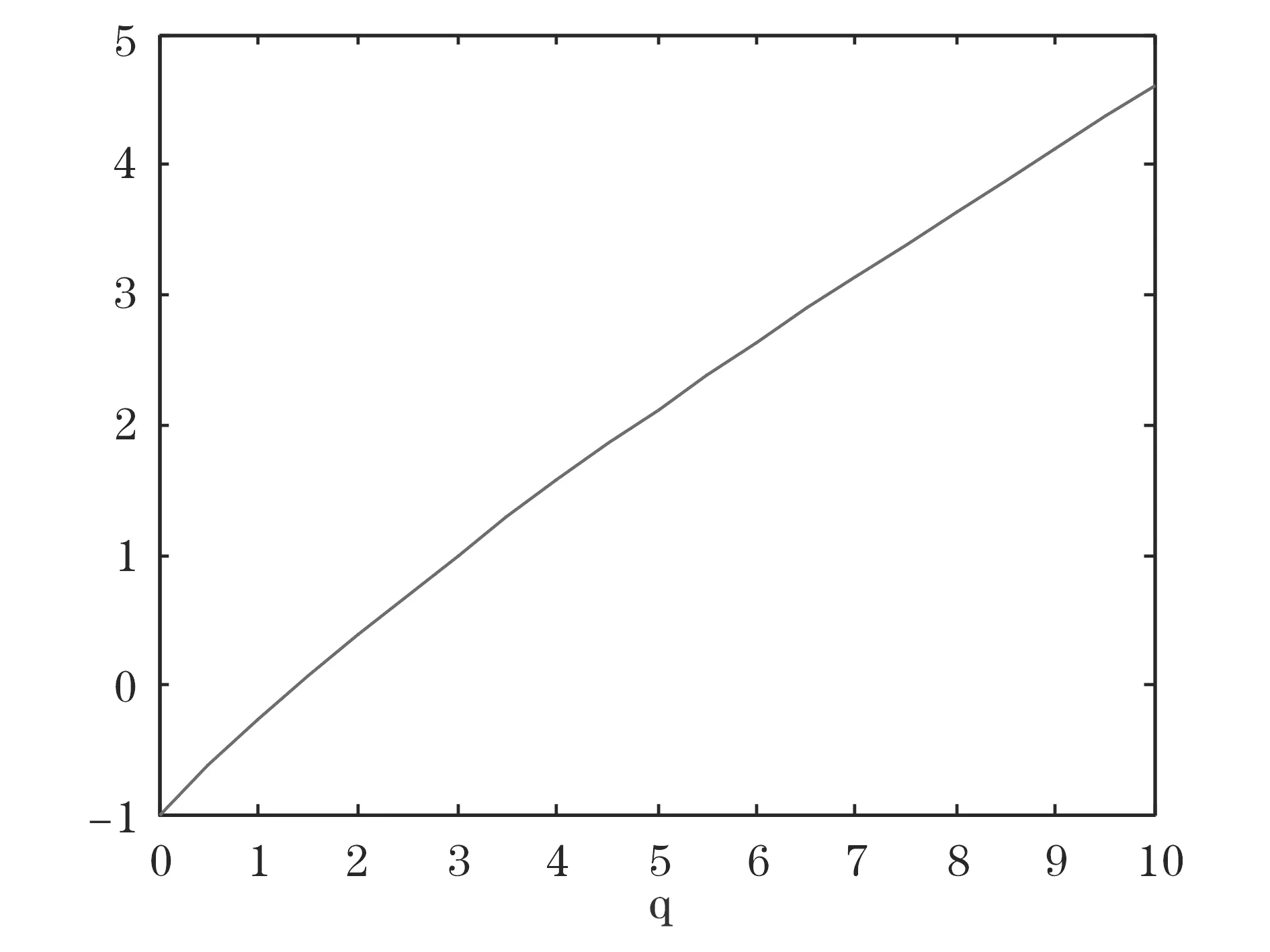
图5 BDI指数序列尺度函数

(二)干散货运价指数多重分形结构研究

本文运用多重分形谱分析法，通过对运价指数收益序列多重分形谱的研究，来分析BDI指数多重分形结构的内部特征，如图6所示：

图6 BDI指数序列多重分形谱图

多重分形谱是直接由BDI指数随时间的变化计算出来的，反映了航运市场走势的信息，结合图6和多重分形谱的几何意义，得出BDI 指数的多重分形谱曲线分布范围较大，表明BDI指数波动幅度大，其分布是非均匀的，同时相应的分形谱跨度也较大。多重分形谱图左端明显低于右端，呈密集型分布，揭示出航运市场中BDI指数归一化价格较高的事件起主要作用，BDI指数总体上呈增大趋势。

航运市场受世界经济走势、市场参与人信息掌握程度、自然现象等多种因素的共同影响，导致航运市场的复杂性及运价指数的非线性，这些因素的最终作用结果都通过BDI指数来综合体现，而多重分形结构是目前为止分析时间序列特征最为全面的模型，因此，以上研究得出的航运价格指数的分布特征对航运市场的研究具有重要意义。

四、结论

通过对BDI指数的多重分形结构研究，得出如下结论：

1、多重分形去趋势波动分析法研究结果表明，干散货航运价格指数序列的广义Hurst指数h(q)关于q是单调下降的，q从0变化到10时，h(q)值从0.7828递减到0.5579，显然不是常数，且h(q)值都介于0.5到1之间，说明运价指数序列具有多重分形特征和持续性趋势特性。

2、运用尺度函数特征判断运价指数序列的多重分形特征，结果表明BDI指数序列的尺度函数是凹向横轴的非线性函数，h(0)=-1,进一步证明运价指数系列不是单分形结构，而是更加精细的多重分形结构。

3、BDI指数多重分形谱图呈密集型分布，左端明显低于右端，说明航运市场中BDI指数归一化价格高的事件起主导作用，BDI指数总体呈增大趋势。

本文通过对运价指数收益序列的广义Hurst指数h(q)、质量指数τ(q)和多重分形谱等特征的研究，证明BDI指数序列不是单分形结构而是更精细的多重分形结构，为更深入研究航运市场价格的分形属性的拐点特征奠定了基础。同时为分析航运价格波动的内在规律和局部特性提供依据，有助于更准确地把握航运市场发展趋势，并以此为航运市场营运人做出正确决策提供帮助，进而大大降低决策风险。

[1] 万九文，吕靖，魏方等.国际干散货运输市场分形特征[J].大连海事大学学报，2010，36(3):31-34.

[2] 李电生，万培祥，员丽芬.干散货航运价格指数分形结构研究[J].北京交通大学学报，2012，11(3):51-56.

[3] Ghashghaie S,Breymann W ,Peinke J. Turbulent cascade in foreign exchange market[J],Nature,1996,381(7): 767-771.

[4] Skjeltorp JA. Scaling in the Norwegian stock market [J].Physical A,2000,283(3-4):486-528.

[5] 张永东，毕秋香.中国股票市场多标度行为的实证分析[J].预测，2002,21(4)：56-59.

[6] 何建敏，朱林，常松.中国股票市场价格波动的尺度特性[J].中国管理科学，2003,(1):1-5.

[7] Schmitt F,Shertze D,Lovejoy S. Multi-fractal Fluctuations in Finance[J].International Journal of Theoretical and Applied Finance,2000,3(3):361-364.

[8] Ausloos M,Ivanovab K. Multiracial nature of stock exchange prices[J]. Computer Physics Communications,2002,147(1): 582-585.

[9] 朱林，常松，何建敏.我国股票市场多仿射性研究[J].管理工程学报，2002,16(3):86-90.

[10] 于建玲，臧保将，尚朋见.股市时间序列的多重分形分析[J].北京交通大学学报，2006,30(6):69-72.

[11] 李海洋，王磊.基于MF-DFA的股市多重分形结构研究[J].湖南工程学院学报，2010,20(3):45-48.

[12] Matia K,Ashkenazy Y. Multiracial properties of price fluctuations of stocks and commodities [J],Euro physics Letter,2003,61(3):422-428.

[13] Norouzzaden P,Rahmani B. A multiracial detrended fluctuation description of Iranian rial-US dollar exchange rate[J],Physical A,2006,367:328-336.

[14] 袁平平，于建玲，尚朋见.股市时间序列的多重分形消除趋势分析[J].北京交通大学学报，2007,31(6):69-72.

[15] 陈洪涛，顾荣宝，周德群.基于MF-DFA的国际原油价格多重分形特征研究[J].复杂系统与复杂性科学，2009,6(3):40-48.

AnalysisofMulti-FractalCharacteristicsofShippingPriceIndexofDryBulk

Li Diansheng,Li Yunhong,Wan Peixiang

(College of Economics,Ocean University of China,Qingdao 266100,China)

Based on the multi-fractal theory,this paper explores the distribution structure of the shipping price index of dry bulk,and estimates the generalized Hurst exponent and mass index. The results show that the time series of the shipping price index of dry bulk have multi-fractal characteristics. Meanwhile,combined with the multi-fractal spectrum analysis,the paper studies the internal structure of the freight index,and finds that the left end of the multi-fractal spectrum is obviously lower than the right end,and that the distribution is intensive,indicating that the shipping price index of dry bulk shows an overall growth trend.

shipping price index; multi-fractal theory; multi-fractal spectrum analysis

F250

A

1672-335X(2013)03-0007-05

责任编辑：王明舜

2012-12-26

国家社科基金项目“FFA在中国相关航线上的市场效率研究”(09BJY074)

李电生(1966- )，男，河北石家庄人，中国海洋大学经济学院副教授，主要从事现代物流与供应链管理，港口规划与管理研究。