具有阶段结构的捕食－食饵模型的定性分析

姚若飞，李艳玲

（陕西师范大学 数学与信息科学学院，陕西 西安710062）

文献［1－3］讨论了捕食者具有阶段性结构的捕食与被捕食模型

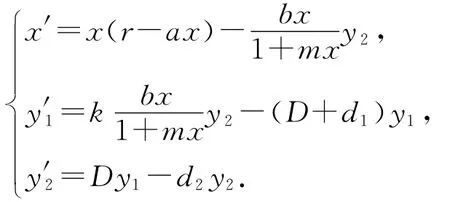
其中x（t）、y1（t）、y2（t）分别表示在时刻t食饵的种群密度、不成熟的和成熟的天敌种群密度．他们讨论了该常微分系统的一致持久性、正平衡态的存在性，及一定条件下的全局渐近稳定性和周期解的存在性与稳定性．

考虑到实际问题中种群密度与地域具有一定关系，因此本文讨论如下的反应扩散模型：

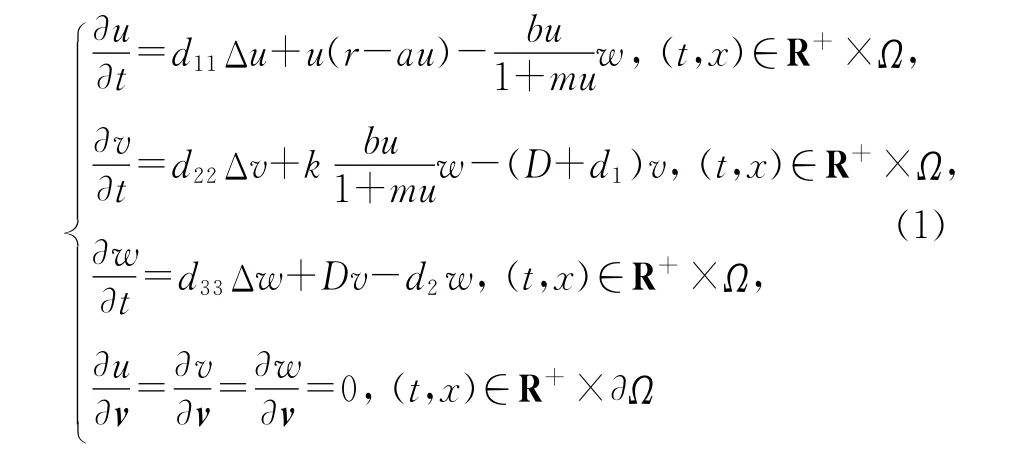
及初值条件

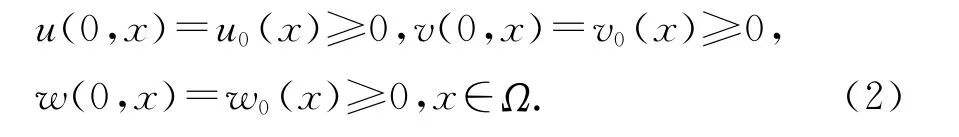
其中u0、v0、w0∈C2（Ω）∩C（¯Ω）．这里Ω是Rn中的一个光滑区域，u（t，x）、v（t，x）、w（t，x）分别表示在时刻t、位置x处食饵的种群密度、不成熟的和成熟的天敌种群密度，v表示边界∂Ω上的单位外法向量，d11、d22、d33＞0是扩散系数，r、a、b、m、k、D、d1、d2都为正常数．

为方便讨论稳态解问题，记d11＝d22＝d33＝d，这实际上也是各个参数的一个转化，于是得到

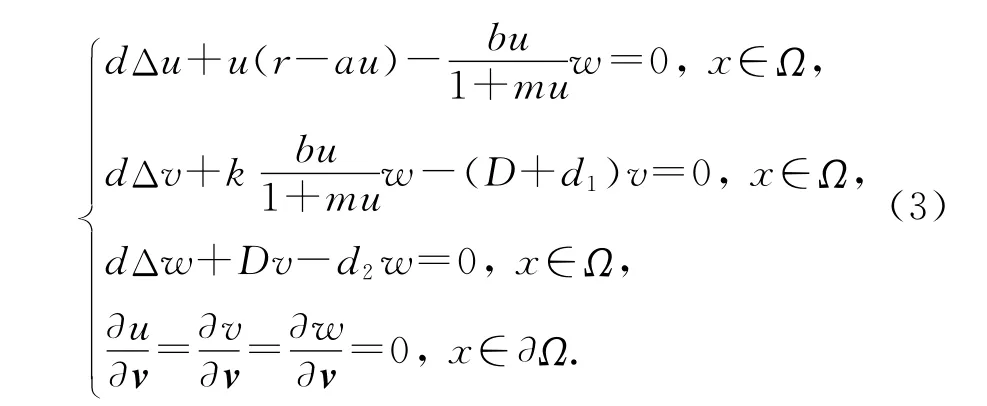
容易计算，系统（1）有一个平凡的常数稳态解U0（0，0，0）和一个半平凡的常数稳态解U1（r／a，0，0），另外当满足条件时，系统（1）还有一个正的常数稳态解U＊（u＊，v＊，w＊），这里

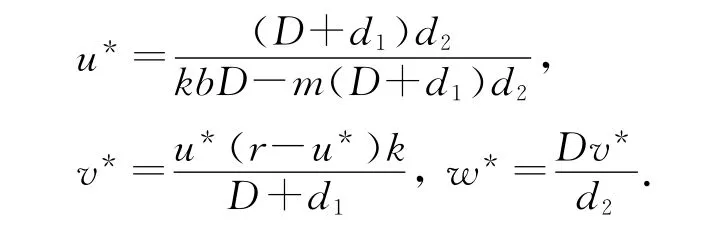
1 整体解的存在性和全局稳定性

初边值问题（1）－（2）的解是局部存在唯一的［4］，这里只讨论整体解的存在性．注意到两类捕食者之间是互惠关系［5］，因此对v、w的方程，方程组比较原理是成立的，于是有如下两个结论：

定理1 设（u，v，w）∈C2（［0，T）ׯΩ，R3）是系统（1）－（2）的一个解，那么（u，v，w）是非负的，并且有一个至多是T的指数函数的上界．

定理2 设d2（D＋d1）（a＋mr）＞kbrD．如果（u，v，w）∈C2（［0，∞）ׯΩ，R3）是系统（1）－（2）的一个正解，则对x一致地有

定理1和定理2的证明 易知［0，＋∞）3是系统（1）的一个不变区域，故（u，v，w）非负，并且当且仅当u0≢0时，u＞0，∀t＞0，x∈¯Ω；当且仅当v0≢0或w0≢0时，v、w＞0，∀t＞0，x∈¯Ω．下面讨论正解情形，设U（t）是常微分系统

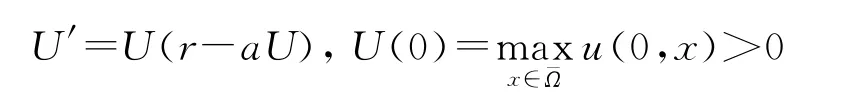
的解，那么当t→＋∞时，U（t）→r／a．对比u的方程，利用单个方程的比较原理知

从而u有界．注意到bu／（1＋mu）＜b／m，令（V（t）、W（t））是线性常微分系统

的解，于是（V（t），W（t））至多指数增长．因为（v，w）的方程是互惠的，由方程组的比较原理得

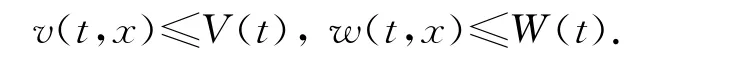
所以，（u，v，w）有界并且有一个至多是T的指数函数的上界，从而系统（1）－（2）的解是整体存在的．

在定理2的条件下，存在R＞r，使d2（D＋d1）（a＋mR）＞kbRD．并且对x一致地有

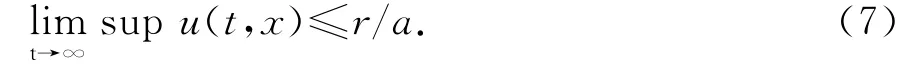
取T1＞0使得当t≥T1时，u（t，x）≤R／a．构造（V（t），W（t））如（6），初值为T1时刻代替，则由R的取法知（V（t），W（t））指数收敛于（0，0）．从而由比较原理可知，v（t，x）≤V（t），w（t，x）≤W（t），t≥T1，x∈¯Ω．于是

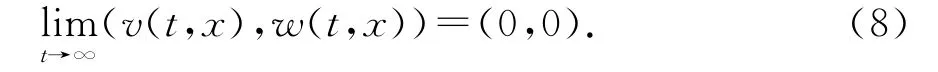
对任意的ε∈（0，r／ab），取T2＞T1，使得当t≥T2时v（t，x）＜aε．令u～（t）如下：

因为bwu／（1＋mu）≥abεu（当t≥T2时），利用u的方程及比较原理，得

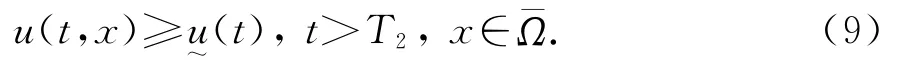
注意到u～（t）→r／a－bε，及（7）－（9）和ε的任意性知定理2的结论成立．

2 正解的先验估计和非常数正解的不存在性

本节应用一个与最大值原理有关的引理，讨论正解的估计，利用这个估计和能量积分方法得到一个非常数正解的不存在性结果．

引理1［6］设F（x，w）∈C（¯Ω×R1）．若w∈C2（Ω）∩C1（¯Ω）满足

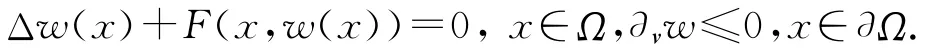
如果w（x0，那么F（x0，w（x0））≥0．

定理3 设（u，v，w）是系统（3）的一个正解，则0＜u＜r／a，0＜v＜K，0＜w＜K，x∈¯Ω．

其中K是一个与m、b、d无关的正常数．

令V＝ku＋v，则它满足

于是得到

定理4 存在一个仅依赖r、a、b、k、D、d1、d2、Ω的正常数D，使得当d＞D时，系统（3）的正解一定为正常数．

证明 若φ∈L1（Ω），记ˉφ＝∫Ωφ（x）dx／｜Ω｜和φ＝φ－ˉφ．令n（u）＝u（r－au），f（u，w）＝buw／（1＋mu）．如果（u，v，w）是系统（3）的一个正解．对（3）中3个方程分别乘以u、v、w后，再在Ω 上积分，利用Green公式，得

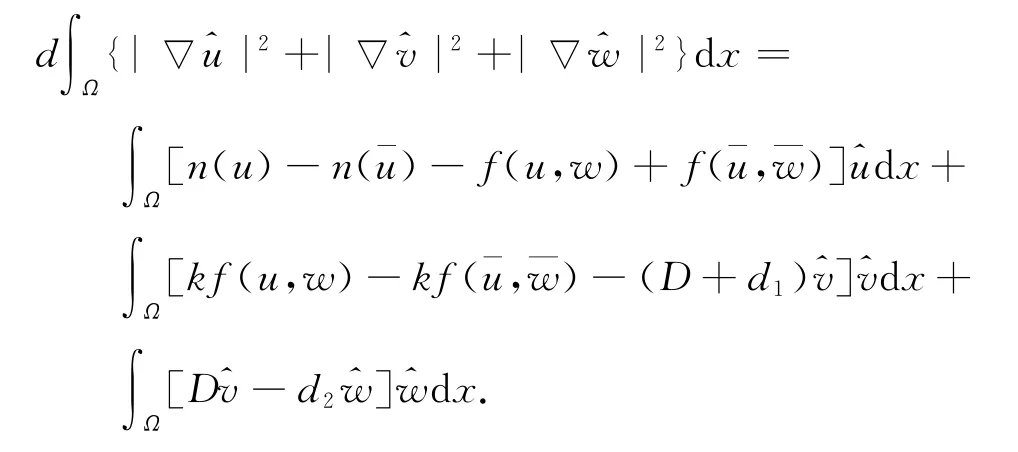
注意到n（u）－n（u）＝g1u，f（u，w）＋f（ˉu，ˉw）＝g2u＋g3w，这里g1、g2、g3都是函数且有不依赖于m和d的上界（已用到定理3），那么

结合Poincar˙e不等式

∫Ω｜φ－ˉφ｜2dx≤CΩ∫Ω｜▽φ｜2dx，∀φ∈W1，2（Ω）和Young不等式，得

上式表明，当d＞CΩK1（K1不依赖于m和d）时，u＝v＝w＝0，即u、v、w都是常函数．

3 常数稳态解处的局部分歧

本节讨论系统（3）在3个常数平衡态的局部分歧，其主要是验证局部分歧定理（文献［8］中定理13．5）中的3个条件成立．

设0＝λ0＜λ1≤λ2≤…→＋∞是－Δψ＝λψ，x∈Ω，∂vψ＝0，x∈∂Ω （10）的所有特征值，相对应的单位正交化的特征函数依次为ψ0，ψ1，ψ2，…．ψ0是主特征函数，为正函数，其他特征函数均变号．

Hilbert空间［L2（Ω）］3具有内积〈U，V〉＝，U＝（u1，u2，u3）T，V＝（v1，v2，v3）T，以后讨论中出现垂直（符号为⊥）的概念就是在这种意义下的．记

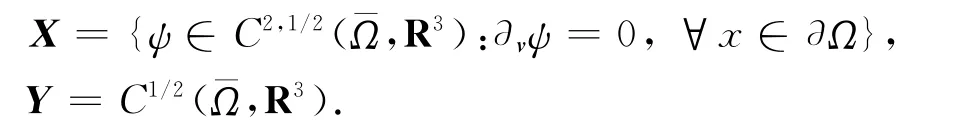
它们在通常的范数意义下都是Banach空间．设U＝（u，v，w），

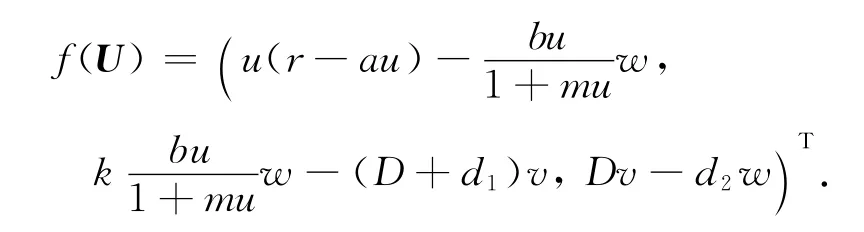
定义光滑算子F：R＋×X→Y为F（d，U）＝dΔU＋f（U）．那么系统（3）转化成

则FU（d，U）＝dIΔ＋H（U）：X→Y，FdU（d，U）＝IΔ：X→Y，其中

先计算算子L＝IΔ＋H：X→Y的一些性质（H是实矩阵，HT表示H的转置）．设U∈Ker（L），并记于是有

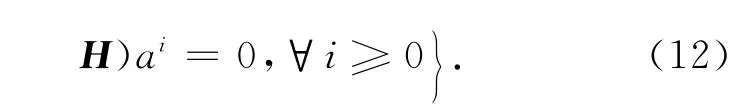
上述的求和实际上是有限和，而R（L）＝｛f∈Y：f⊥Ker（L＊）｝，L＊＝IΔ＋HT，故

由此，Ker（L）∩R（L）＝ ｛0｝的充要条件是对每一个i，λi（关于矩阵H）的代数重数和几何重数相等（可能都为0）．这里（12）式用来计算L的核空间，（13）式用来判断L的像空间的余维数，而（14）式是在以后的情形中用来判断分歧定理第三个条件的．

在高维空间中，特征问题（10）的正特征值的重数可能大于1．然而在一维区间时，所有特征值都是单重的，这里讨论空间为一维的情形：

对平衡态U0（0，0，0）和U1（r／a，0，0），F（d，U0）＝F（d，U1）＝0，∀d＞0．

显然，H0的正特征值只有一个，即为r，并且代数重数是1，以及0不是特征值；当d2（D＋d1）（a＋mr）＜kbrD时，H1的正特征值只有一个，记为σ，并且代数重数是1，以及0不是特征值．对于这两种平衡态，其分歧情形是相似的．

定理5 给定j≥1和d＝r／λj，则存在δ＞0和光滑曲线（d，φ）：（－δ，δ）→R×Z满足：（ⅰ）φ（0）＝0，d（0）＝d，（ⅱ）F（d（s），U（s））＝0，s∈ （－δ，δ）；（ⅲ）在（d，U0）的某个小邻域内（11）的每个解要么在这条曲线上，要么是平凡的．这里Φ＝ξψj，Z＝｛φ∈X：φ⊥Φ｝，ξ＝ （1，0，0）T是H0的正特征值所对应的“唯一”特征向量及

U（s）＝U0＋s（Φ＋φ（s））．

证明 设L0＝FU（d，U0）＝＋H0，L1＝IΔ，则由（12）得，Ker（L0）＝span｛Φ｝，Φ ＝ξψj，L1Φ＝－λjΦ．再由（13）和（14）式得，codimR（L0）＝1，L1Φ ＝－λjΦ ∉R（L0）．分歧定理的条件成立．

定理6 设条件（4）成立，且记σ是H1上的唯一正特征值．给定j≥1和d＝σ／λj，则存在δ＞0和光滑曲线（d，φ）：（－δ，δ）→R×Z满足：（ⅰ）φ（0）＝0，d（0）＝d；（ⅱ）F（d（s），U（s））＝0，s∈（－δ，δ）；（ⅲ）在（＾d，U1）的某个小邻域内系统（11）的每个解要么在这条曲线上，要么是平凡的．这里Φ＝ξψj，Φ＝ξψj，Z＝｛φ∈X：φ⊥Φ｝，ξ、ξ是H1和HT1的正特征值所对应的“唯一”特征向量及

下面讨论正常数平衡态U＊处的分歧，记

那么矩阵H＊的特征多项式是

注意到r－au＊＞0，那么H＊至少有一个负特征值，0不是特征值，并且它的正特征值（若有的话）必然是两个．假设

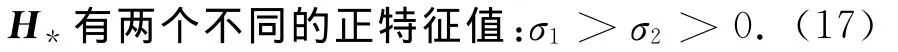
为避免σ1／λj＝σ2／λi的情形，进一步设

同样地，有下述分歧结论：

定理7 设条件（4）、（17）、（18）成立．给定i∈｛1，2｝，j≥1．记d＝σi／λj，则存在δ＞0和光滑曲线（d，φ）：（－δ，δ）→R×Z满足：（ⅰ）φ（0）＝0，d（0）＝d；（ⅱ）F（d（s），U（s））＝0，s∈（－δ，δ）；（ⅲ）在（＾d，U＊）的某个小邻域内（11）的每个解要么在这条曲线上，要么是平凡的．这里Φ＝ξψj，Φ＝ξψj，Z＝ ｛φ∈X：φ⊥Φ｝，ξ、ξ是H＊和HT＊的正特征值σi所对应的“唯一”特征向量及

U（s）＝U＊＋s（Φ＋φ（s））．

证明 同前面定理证明一样，这里只需要验证单特征值分歧定理的第三个条件，事实上，σi（i＝1，2）是H＊的代数单重特征值就表明ξ·ξ≠0．从而结论得证．

注1 取参数值b＝1、m＝1、D＝1、d1＝0．1、d2＝0．2、k＝1、a＝2、r＝12时，U＊＝（0．282 1，2．932 3，14．661 4），H＊的特征值为－1．634 7，1．469 7，0．816 8．这表明条件（17）在某些参数的时候是可以成立的，而条件（18）只要合适地扰动参数值也可以成立．

［1］Wang Wendi．Global dynamics of a population model with stage structure for predator［C］∥Chen Lansun．Advanced Topics in Biomathematics．River Edge：World Scientific Publishing，1998：253－257．

［2］Xiao Yanni，Chen Lansun．Global stability of a predator－prey system with stage structure for the predator［J］．Acta Mathematica Sinica，2004，20（1）：63－70．

［3］Georgescu Paul，Hsieh Ying－Hen．Global dynamics of a predator－prey model with stage structure for the predator［J］．SIAM Journal on Applied Mathematics，2007，67（5）：1379－1395．

［4］Avner Friedman．Partial differential equations of parabolic type［M］．Prentice－Hall：Englewood Cliffs，1964．

［5］叶其孝，李正元．反应扩散方程引论［M］．北京：科学出版社，1990：192－235．

［6］Lou Yuan，Ni Weiming．Diffusion，self－diffusion and cross－diffusion［J］．Journal of Differential Equations，1996，131（1）：79－131．

［7］Jang Jaeduck，Ni Weiming，Tang Moxun．Global bifurcation and structure of turing patterns in the 1－D Lengyel－Epstein model［J］．Journal of Dynamics and Differential Equations，2004，16（2）：297－320．

［8］Smoller J．Shock waves and reaction－diffusion equations［M］．New York：Springer－Verlag，1994：167－191．

［9］马翠，李艳玲．一般的Gause型捕食－食饵模型的定性分析［J］．陕西师范大学学报：自然科学版，2010，38（3）：6－9．

［10］Wu Jianhua．Global bifurcation of coexistence state for the competition model in the chemostat［J］．Nonlinear Analysis，2000，39（7）：817－835．