具有阶段结构、时滞和接种的幼年染病单种群模型的稳定性

王 烈，陈斯养

（陕西师范大学 数学与信息科学学院，陕西 西安710062）

文献［1－2］研究了具有阶段结构的单种群模型，作者假设种群从幼年到成年的平均成熟期为一个常数，在模型中将其用一个时滞来表示．疾病的传播主要依赖于疾病本身的特性．例如麻疹、腮腺炎、水痘、猩红热、白喉等疾病主要在幼年人群中传播，而淋病、梅毒等传染病只在成年人群中传播，因此将阶段结构引入到传染病模型中能够更好地反映实际情况．文献［3－10］研究了具有阶段结构的传染病模型，得到平衡点稳定的充分条件及平衡点处发生Hopf分支等动力学行为．文献［1－7］中用rx2（t－τ）exp（－d1τ）表示在t－τ时刻出生的幼年并且存活到时刻t的密度；而文献［8－10］用rx2（t－τ）表示在t－τ时刻出生的幼年并且存活到时刻t的密度．为更好地控制疾病，近年来的研究表明接种疫苗是预防和控制疾病传播的主要措施，文献［11－13］讨论了带有接种的传染病模型．

基于以上研究结果，本文主要研究具有阶段结构、时滞和接种的幼年染病单种群模型：

其中x1（t）、I（t）和W（t）分别表示易感染幼年、染病幼年和直接通过接种而产生暂时免疫能力的接种者的种群密度，x2（t）表示成年种群的密度．流行病只在幼年种群中传播，而成年种群不会染病．参数r、d1、α、ρ、μ、ε、d2、β、δ、τ均为正常数，它们的生物意义可以参看文献［3－13］．

1 平衡点的存在性

通过计算，得到系统（1）以下平衡点：

（ⅰ）当R1＞1、R2＞1时，存在地方病平衡点（正平衡点）P1（x＊1，x＊2，V＊，I＊），其中

I＊是方程f（I）－g（I）＝0的唯一正根，其中

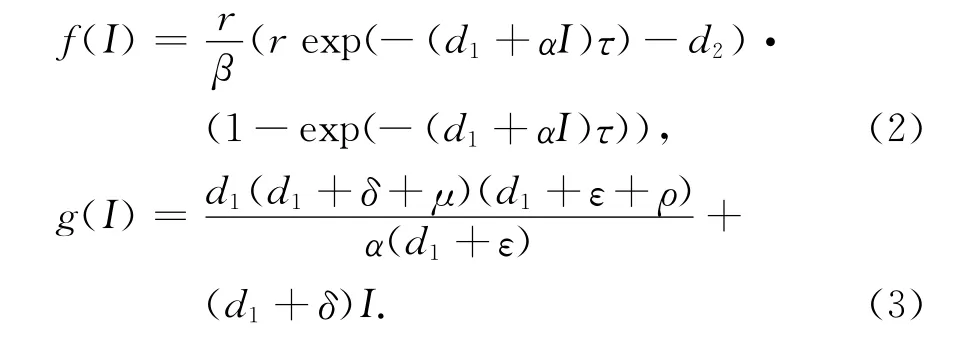
下面证明地方病平衡点的存在性和唯一性．正平衡点P1（x＊1，x＊2，V＊，I＊）满足代数方程组

由方程组（4）的第2、3、4个方程，易得

将它们代入到第1个方程，可得

对函数f（I）求导，可得

通过计算可知，当I＜I0时，函数f′（I）＞0，即当I＜I0时函数f（I）是单调递增的；当I＞I0时，函数f′（I）＜0，即当I＞I0时函数f（I）是单调递减的．函数g（I）在区间（0，＋∞）上是单调递增的．

记τ0＝ln（2）／d1，下面以τ＞τ0和τ＜τ0分别进行讨论：

a）当τ＞τ0时，2－exp（d1τ）＜0，有I0＜0，则函数f（I）在区间（0，＋∞）上是单调递减的．当R1＞1，R2＞1时，f（0）＞g（0）＞0，所以方程（5）一定存在唯一正根I＊．

b）当τ＜τ0时，2－exp（d1τ）＞0，对于r∈（0，d2exp（d1τ）／（2－exp（d1τ））），I0＜0，参照在a）中的讨论可知方程（5）一定存在唯一正根I＊；对于r∈ （d2exp（d1τ）／（2－exp（d1τ）），＋ ∞），I0＞0，则函数f（I）在区间（0，I0）上是单调递增的，在区间（I0，＋∞）上是单调递减的．当R1＞1、R2＞1时，f（0）＞g（0）＞0，所以方程（5）一定存在唯一正根I＊．

对应地可以求出

（ⅱ）当R1＞1、R2＜1或R1＞1、R2＜1、R3＜1时，存在无病平衡点（边界平衡点）P2（x1，x2，V，0），其中

下面以τ＞τ0和τ＜τ0分别进行讨论：

a）当τ＞τ0时，2－exp（d1τ）＜0，有I0＜0，则函数f（I）在区间（0，＋∞）上是单调递减的．当R1＞1，R2＜1时，g（0）＞f（0）＞0，所以方程（5）无实根．

b）当τ＜τ0时，2－exp（d1τ）＞0时，对于r∈（0，d2exp（d1τ）／（2－exp（d1τ））），I0＜0，参照在a）中的讨论可知方程（5）无实根．

c）当τ＜τ0时，2－exp（d1τ）＞0时，对于r∈（d2exp（d1τ）／（2－exp（d1τ）），＋ ∞），I0＞0，则函数f（I）在区间（0，I0）上是单调递增的，在区间（I0，＋∞）上是单调递减的．当R1＞1，R2＜1，R3＜1时，g（0）＞f（0）＞0，g（I0）＞f（I0）＞0，所以方程（5）无实根．

综上所述，可知当R1＞1、R2＜1或R1＞1、R2＜1、R3＜1时，存在无病平衡点（边界平衡点）．将系统（1）中的4个方程相加，可得

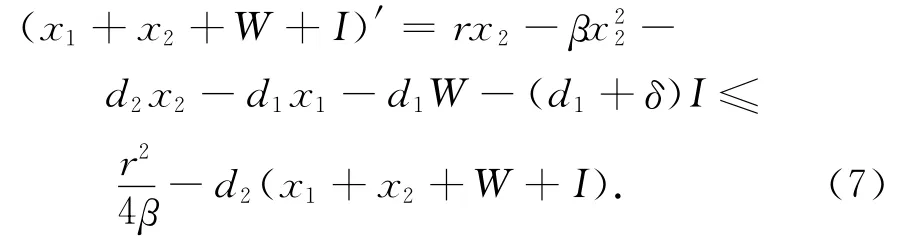
则通过计算可知

通过以上讨论，可得以下引理：

引理1 集合Ω是系统（1）的正不变集．

以下仅在集合Ω上讨论系统（1）的动力学行为．

2 平衡点的稳定性分析

通过计算可知，系统（1）线性近似系统的特征根出现等于零的情况，因此下面通过构造Liapunov函数的办法讨论系统（1）平衡点的稳定性．

定理1 当R1＞1、R2＜1或R1＞1、R2＜1、R3＜1时，无病平衡点是全局渐近稳定的．

证明 当R1＞1、R2＜1或R1＞1、R2＜1、R3＜1时，无病平衡点P2存在．当R2＜1时，可知x1＜x＊1．定义集合Ω1＝ ｛（x1，x2，W，I）｜（x1，x2，W，I）∈

下面在区域Ω1内讨论系统（1）的稳定性．因为当x1＜x＊1时，从系统（1）的第4个等式可知：I＝I（t）在Ω1区域上是单调递减的且t→＋∞时I→0．根据极限系统理论，系统（1）的动力学性态等价于系统

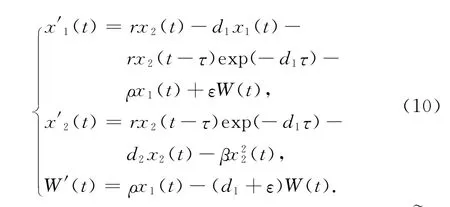
当R1＞1时，系统（10）存在唯一平衡点P1（x1，x2，V），其中

则系统又等价于

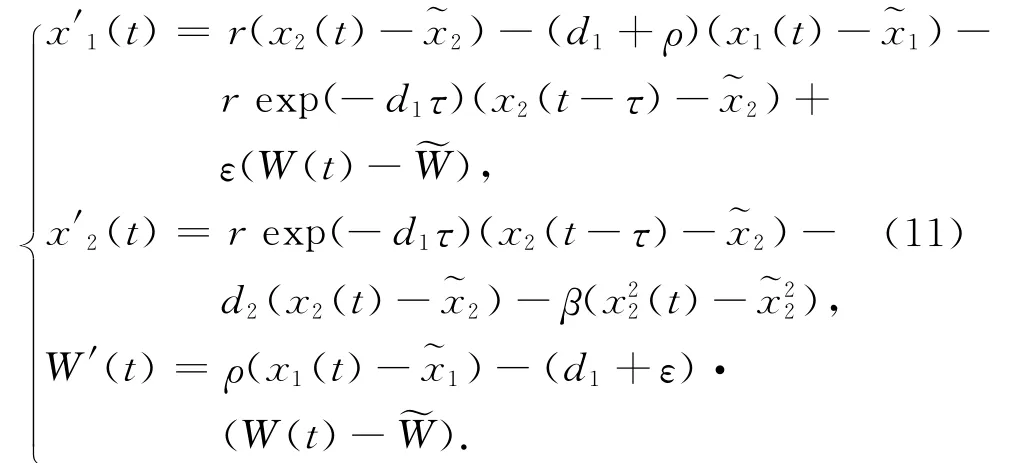
定义Liapunov函数

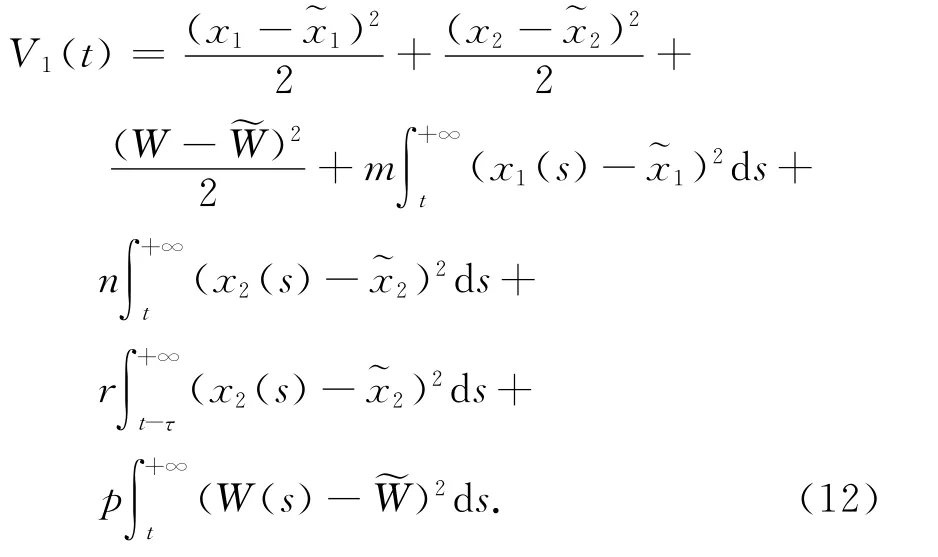
其中m、n、p均为正数．

对V1沿系统（11）求右上导数，可得

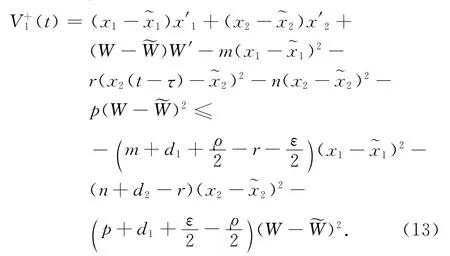
对（14）式在区间［0，t］上积分，变形可得

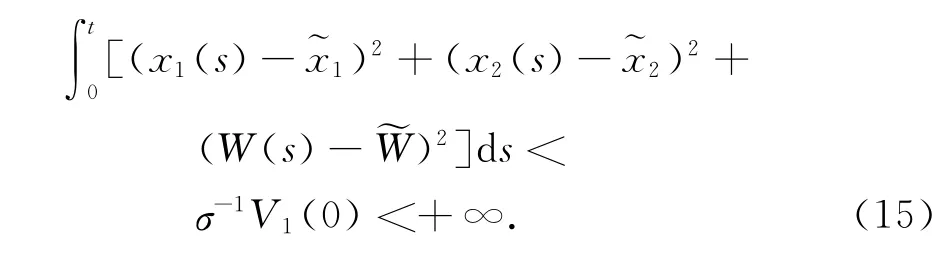
根据文献［14］的方法，可知平衡点P1是全局渐近稳定的．

由R1＞1、R2＜1可推出r∈ （r0，r1）；由R1＞1、R3＜1可知存在实数r2＞0，r∈ （r0，r2）．

由定理1可得如下推论：

推论1 若τ0＜τ，则当r0＜r＜r1时，无病平衡点P2是全局渐近稳定的．

推论2 若τ0＞τ，则当r0＜r＜r2＜r1时，无病平衡点P2是全局渐近稳定的．

推论1和推论2说明，在一定的接种率下，且整个种群的生育率位于某一区间时，疾病将趋于灭绝，而且生育率的区间长度随接种率的提高而随之扩大，随时滞的增加而随之缩小．

定理2 当R1＞1、R2＞1时，正平衡点P1是全局渐近稳定的．

证明 由前面分析可知，当R1＞1、R2＞1时，平衡点P1存在．对系统（1）进行变形，可得

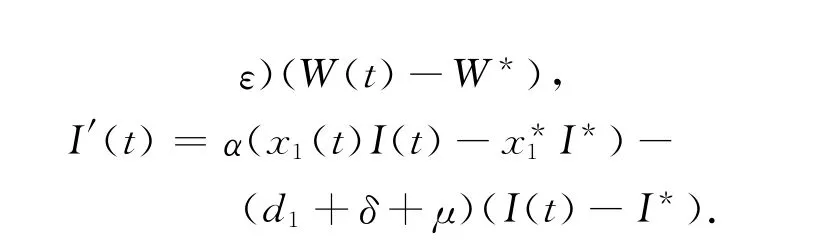
定义Liapunov函数为

其中m、n、q、p均为正数．

对V2沿系统（16）求右上导数，可得

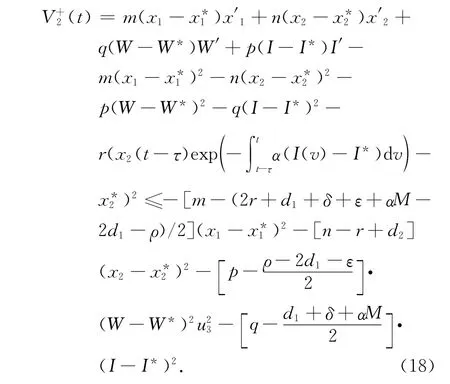
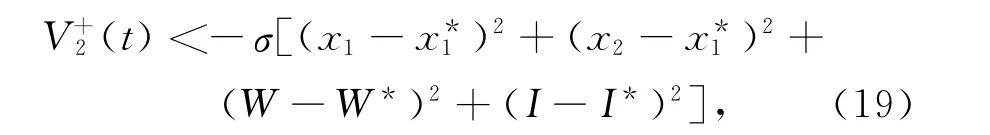
对（19）式在区间［0，t］上积分，变形可得

根据文献［14］的方法，可知平衡点P1是全局渐近稳定的．

由前面分析并结合定理2可得如下推论：

推论3 当r＞r1，正平衡点P1是全局渐近稳定的．

推论3说明，在一定的接种率下，且种群的生育率高于某一阈值时，正平衡点全局渐近稳定，疾病将成为地方病．

3 结语

本文提出一类具有阶段结构、时滞和接种的幼年染病单种群模型，研究了存在正平衡点和无病平衡点的充分条件，证明了正平衡点的唯一性．由于该单种群线性近似系统的特征根出现等于零的情况，所以通过构造Liapunov函数的办法讨论单种群系统平衡点的稳定性，得到了正平衡点和无病平衡点保持全局渐近稳定的充分条件．通过讨论可知，在一定的接种率下，且整个种群的生育率位于某一区间时，疾病最终将趋于灭绝，而且生育率的区间长度随着接种率的提高而随之扩大；随着时滞的增加而随之缩小．当种群的生育率高于某一阈值时，正平衡点全局渐近稳定，疾病将最终成为地方病．结果表明时滞和接种因素在模型中有着非常重要的地位．

［1］Aiello W G，Freedman H I．A time delay model of single－species growth with stage structure［J］．Mathematics Bioscience，1990，101（1）：139－153．

［2］Aiello W G，Freedman H I，Wu J．Analysis of a model representing stage structured populations growth with state－dependent time delay［J］．SIAM Journal of Applied Mathematics，1992，52（3）：855－869．

［3］Xiao Yanni，Chen Lansun．On an SIS epidemic model with stage structure［J］．Journal of Systems and Science Complexity，2003，16（2）：275－288．

［4］Xiao Yanni，Chen Lansun．An SIS epidemic model with stage structure and a delay［J］．Acta Mathematicae Applicatae Sinica（English Series），2002，18（1）：607－618．

［5］Song Xinyu，Chen Lansun．Modeling and analysis of a single－species system with stage structure and harvesting［J］．Mathematics and Computer Modeling，2002，36（1）：67－82．

［6］Song Xinyu，Chen Lansun．Optimal harvesting policy and stability for single－species growth model with stage structure［J］．Journal of Systems and Science Complexity，2002，15（2）：194－201．

［7］Liu Li，Li Xiangao，Zhuang Kejun．Bifurcation analysis on a delayed SIS epodemic model with stage structure［J］．Electronic Journal of Differential Equations，2007，2007（77）：1－17．

［8］石瑞青，陈兰荪．具有阶段结构和时滞的幼年染病单种群模型研究［J］．大连理工大学学报，2010，50（2）：304－308．

［9］Wang Jiaoyan，Lua Qishao，Feng Zhaosheng．A nonautonomous predator－prey system with stage structure and double time delays［J］．Journal of Computational and Applied Mathematics，2009，230（1）：283－299．

［10］Agarwal M，Devi S．A time－delay model for the effect of toxicant in a single species growth with stage－structure［J］．Nonlinear Analysis：Real World Applications，2010，11（4）：2376－2389．

［11］Li Jianquan，Ma Zhien．Qualitative analyses of SIS epidemic model with vaccination and varying total population size［J］．Mathematical and Computer Modelling，2002，35（11／12）：1235－1243．

［12］Li Jianquan，Ma Zhien．Stability analysis for SIS epidemic models with vaccination and constant population size［J］．Discrete and Continuous Dynamical Systems－Series B，2004，4（3）：635－642．

［13］杨亚莉，李建全，张吉广．一类带有接种的传染病模型的全局性分析［J］．西北大学学报：自然科学版，2009，39（5）：729－731．

［14］Beretta E，Takeuchi Y．Global asymptotic stability of Lotka－Volterra diffusion models with continuous time delays［J］．SIAM Journal on Applied Mathematics，1988，48（3）：627－651．