Smarandache－Pascal派生逆序列的几个恒等式

赵院娥，刘 卓

（1延安大学 数学与计算机学院，陕西 延安716000；2西北大学 数学系，陕西 西安710127）

对任意基序列｛bn｝，定义它的Smarandache－Pascal派生序列｛Tn｝为T1＝b1，T2＝b1＋b2，T3＝b1＋2b2＋b3，一般地

文献［1］详细介绍了Smarandache－Pascal派生序列的定义及其性质，同时还提出了一系列有趣的命题和猜想，例如猜测当｛bn｝＝ ｛F8n＋1｝＝ ｛F1，F9，F17，F25，…｝及n≥2时有恒等式

其中｛Fn｝表示著名的Fibonacci数列．

最近，有不少学者研究了Smarandache－Pascal派生序列的性质以及文献［1］中提出的猜想，他们不仅解决了这些问题，同时又将文献［1］中的内容进行了推广和延伸，给出了一般性的结论．本文的主要目的是引入Smarandache－Pascal派生逆序列，进而研究它的各种性质． 为此， 先引入Smarandache－Pascal派生序列的逆序列的定义：对任意序列｛Tn｝，定义b1＝T1，b2＝T2－T1，当n≥2时：

这一序列之所以称为Smarandache－Pascal派生序列的逆序列是因为当且仅当bn＋1＝这一性质不难用数学归纳法证明．本文对这一序列的性质进行研究，并利用初等及组合方法得到几个有意义的恒等式．

1 预备知识

为叙述方便，先给出二阶线性递推数列的一个简单结论：

引理1 设整数m≥0及n≥2．如果数列｛Xn｝满足递推关系Xn＋2＝aXn＋1＋bXn（n≥0），那么有恒等式Xm＋n＝An－1Xm＋1＋bAn－2Xm．其中An定义为A0＝1．A1＝a及An＋1＝aAn＋bAn－1，n≥1．或者计算公式

证明 用归纳法．注意到递推公式Xm＋2＝aXm＋1＋bXm，A1＝a，A0＝1，An＋1＝aAn＋bAn－1，n≥1．所以Xm＋2＝A1Xm＋1＋bA0Xm．即就是当n＝2时引理1成立．因为Xm＋3＝aXm＋2＋bXm＋1＝a（aXm＋1＋bXm）＋bXm＋1＝ （a2＋b）Xm＋1＋baXm＝A2Xm＋1＋bA1Xm．即当n＝3时引理1成立．假定引理1对所有整数2≤n≤k成立，即就是Xm＋n＝An－1Xm＋1＋bAn－2Xm．则当n＝k＋1时，由Xm的递推关系及归纳假设有

就是说当n＝k＋1时引理1成立．

2 主要结果

定理1 设｛Xn｝是一个二阶线性递推数列且X0＝u，X1＝v，对所有n≥1，Xn＋1＝aXn＋bXn－1，其中a2＋4b＞0．那么对任意正整数d≥1，当

时有恒等式

其中｛An｝定义为A0＝1，A1＝a，An＋1＝aAn＋bAn－1，n≥1．事实上An的表示式为

证明 对任意正整数d，由bn的定义及二项式系数的性质

应用引理1，有Xdk＋d＋1＝AdXdk＋1＋bAd－1Xdk，再应用 （2）式及bn的定义可以推出

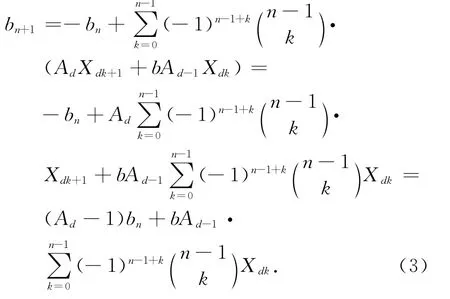
另一方面，由引理1也有Xdk＋d＝Ad－1Xdk＋1＋bAd－2Xdk，于是应用这个递推关系及公式（1）有

由（3）式也可推出恒等式

再结合（3）、（4）及（5）式可以得到

由An的计算公式易得到恒等式

将其代入（6）式可以推出

于是完成了定理1的证明．

若取b＝1，由定理1可得到下面的：

推论1 设｛Xn｝是一个二阶线性递推序列且X0＝u，X1＝v，Xn＋1＝aXn＋Xn－1，n≥1．对任意正整数a及偶数d≥2， 定义它的Smarandache－Pascal派生逆序列为

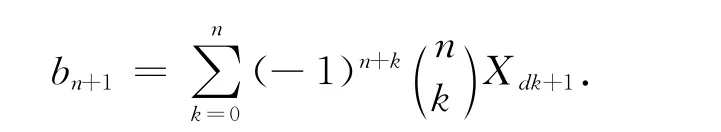
那么有递推公式

推论2 设｛Xn｝是一个二阶线性递推序列且X0＝u，X1＝v，Xn＋1＝aXn＋Xn－1，n≥1．则对任意正整数a及奇数d≥1，定义它的Smarandache－Pascal派生序列的逆序列为

那么有递推公式其中An＝An（a）＝

显然Fn＋1（a）＝An（a）是a的一个多项式，有时也称这个多项式为Fibonacci多项式，因为Fn（1）＝Fn是著名的Fibonacci数．有关Smarandache问题及Fibonacci数的内容可参阅文献［2－6］，这里不再重复．

如果在推论1中取a＝2，X0＝P0＝0，X1＝P1＝1以及Pn＋1＝2Pn＋Pn－1，n≥1．那么Pn就成为Pell数．由推论1也可以推出下面的：

推论3 设Pn表示Pell数．那么对任意偶数d≥2及bn＋1＝，有递推公式bn＋1＝（Pd＋1＋Pd－1－2）（bn＋bn－1），n≥2．

从定理1也不难推出如果｛Tn｝是一个二阶线性递推数列，那么它的Smarandache－Pascal派生逆序列｛bn｝也是一个二阶线性递推数列．

3 结语

本文在前人研究Smarandache－Pascal派生序列的基础上，引入了Smarandache－Pascal派生逆序列的定义，用初等方法和组合技巧研究了它的性质，并且给出了关于Smarandache－Pascal派生逆序列的几个有意义的恒等式，这将有助于对Smarandache－Pascal派生逆序列的进一步认识和研究．

［1］Murthy A，Ashbacher C．Generalized partitions and new ideas on number theory and smarandache sequences［M］．Hexis：Phoenix，2005：79．

［2］Smarandache F．Only problems，not solutions［M］．Chicago：Xiquan Publishing House，1993．

［3］Wiemann M，Cooper C．Divisibility of an F－L type convolution，Applications of Fibonacci numbers［J］．Kluwer Academic Publishers Dordrecht，2004，9：267－287．

［4］Ma Rong，Zhang Wenpeng．Several identities involving the Fibonacci numbers and Lucas numbers［J］．The Fibonacci Quarterly，2007，45：164－170．

［5］Yi Yuan，Zhang Wenpeng．Some identities involving the Fibonacci polynomials［J］．The Fibonacci Quarterly，2002，40：314－318．

［6］Wang Tingting，Zhang Wenpeng．Some identities involving Fibonacci，Lucas polynomials and their applications［J］．Bulletin Mathematique de la Societe des Sciences Mathematiques de Roumanie，2012，55（1）：95－103．