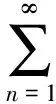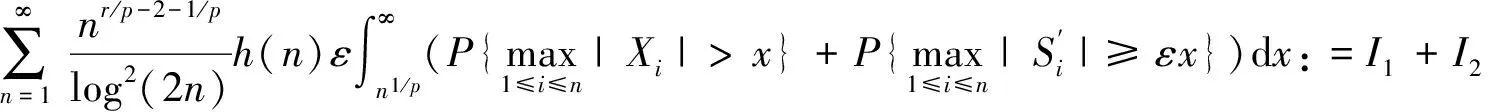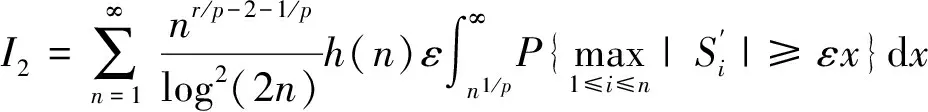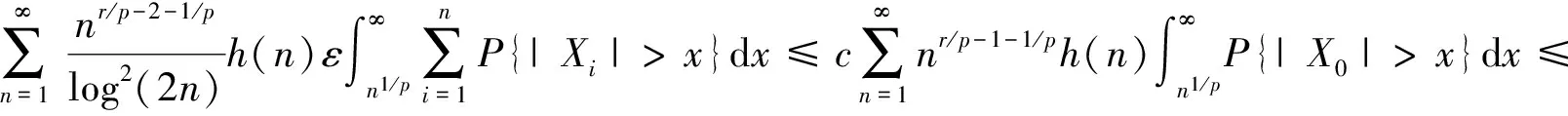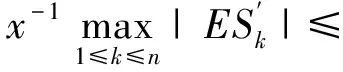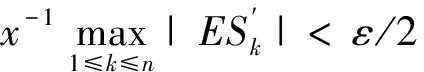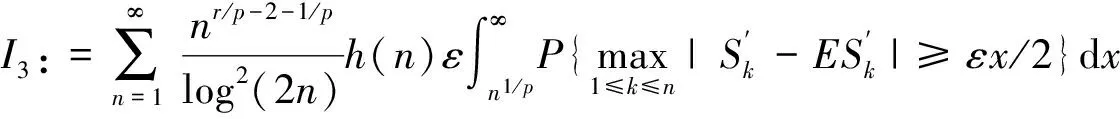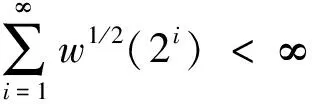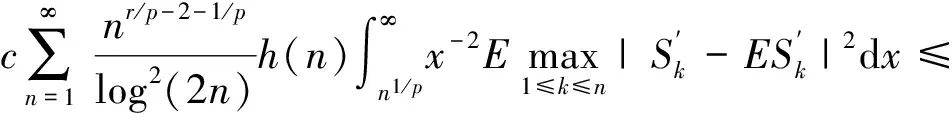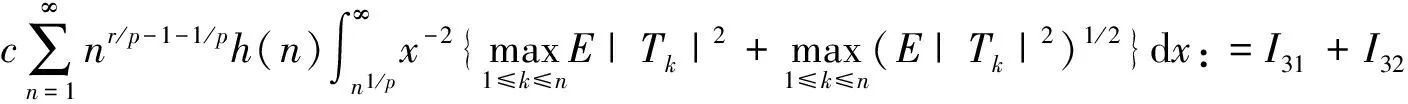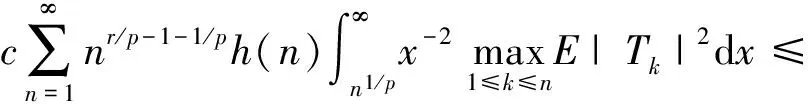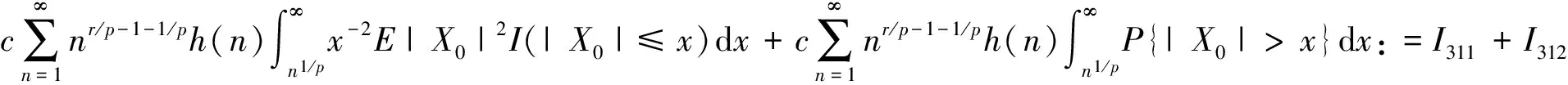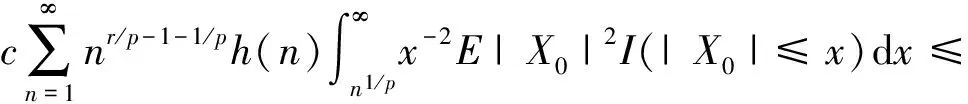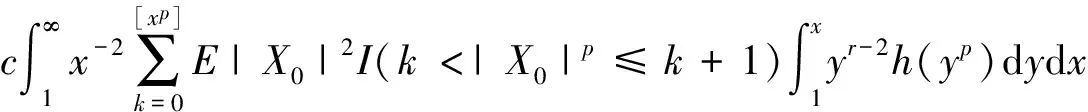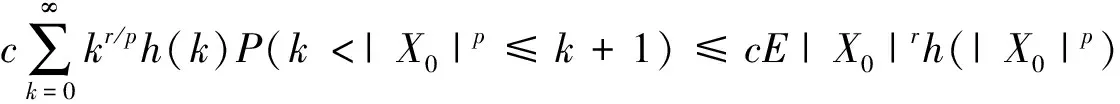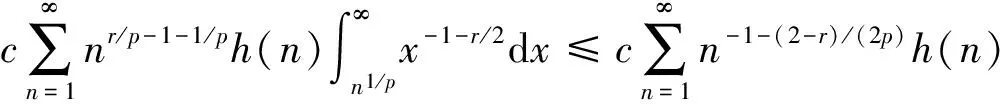两两PQD序列的矩完全收敛性
2013-10-28沈建伟
沈建伟
(浙江科技学院理学院,浙江 杭州 310023)
两两PQD序列的矩完全收敛性
沈建伟
(浙江科技学院理学院,浙江 杭州 310023)
两两PQD列;完全收敛性;矩完全收敛性
0 引 言
完全收敛性是由Hsu和Robbins[1]引入的概率极限理论中的一个重要概念,目前已有许多关于混合随机变量列的完全收敛性的文献.近期关于矩完全收敛性问题也得到了学者的关注并获得不少成果. 设{Xk,k≥1}为一个i.i.d.随机变量序列且均值为零、方差有限,Chow[2]获得了如下的矩完全收敛结果:
定理A假设{Xk,k≥1}为一个i.i.d.的随机变量序列,EX1=0.对于1≤p<2和r>p,若E{|X1|r+|X1|log(1+|X1|)}<∞, 则对∀ε>0,有

王定成等[3]把Chow的结果推广到了p-型Banach空间,得到了矩完全收敛的充分必要条件. Li等[4]和Kim等[5]获得了同分布NA列、φ混合序列的移动平均过程的类似结果.王定成等[6]获得了NA列的矩完全收敛的充分必要条件. 陈平炎等[7]把结果推广到了同分布的ρ混合序列情形. 傅可昂[8]得到了关于同分布PA列的矩完全收敛性.本文把结果推广到了不同分布的两两PQD序列情形.
文中总设c代表正常数, 在不同的地方可以代表不同的值.[x]表示不超过x的最大整数. 记
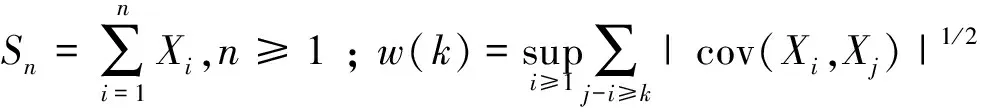
定义1[9]称随机变量X和Y是PQD(positively quadrant dependent)的,若对∀x,y∈R都有
P(X 称随机变量序列{Xn,n≥1}是两两PQD的,若对∀i≠j,Xi与Xj是PQD的. 引理1[9]设随机变量X和Y是PQD的,则 (i)EXY≥EXEY; (ii)若f,g同为非降(或非增)函数,则f(X)与g(Y)仍为PQD的. 引理3[11]设{Xn,n≥1}是任意随机序列.若存在某随机变量X,使对任意x>0及n≥1,有P{|Xn|≥x}≤cP{|X|≥x},则对∀β>0,∀t>0有 E|Xn|βI(|Xn|≤t)≤c(E|X|βI(|X|≤t)+tβP{|X|>t}), E|Xn|βI(|Xn|>t)≤cE|X|βI(|X|>t). (1) 注1由于矩完全收敛性蕴含完全收敛性, 故在定理1的条件下, 式(1)蕴含了 注2在定理1的条件下,由证明过程可知下面结论亦成立: 要证明式(1)成立, 只需要证明 (2) (3) 首先估计I1.由1 cE|X0|rh(|X0|p)<∞. 再估计I2.由0 cx-1nE|X0|rx-(r-1)I(|X0|>x)≤cxp-r→0 ,当x→∞. 因此,对于充分大的x, 有 (4) 故要证I2<∞,只需证 (5) (6) (7) 对于I312, 其证明类似于I1,不赘述, 得 I312<∞. (8) (9) 对于I32, 由Minkowski不等式及E|X0|r<∞(1 (10) 由式(7)、(8)、(9) 可得 I31<∞. (11) 由式(10)、(11)、(6)可知式(5)成立.综上所述,定理1 成立. [1] Hsu P L, Robbins H. Complete convergence and the law of large numbers[J]. Proceedings of the National Academy of Science,1947,33(2):25-31. [2] Chow Y S. On the rate of moment convergence of sample sums and extremes[J]. Bull Inst Math Acad Sinica,1988,16(3):177-201. [3] 王定成,苏淳.B值独立同分布随机变元序列的矩完全收敛性[J].应用数学学报,2004,27(3):440-448. [4] Li Yunxia,Zhang Lixin. Complete moment convergence of moving-average processes under dependence assumptions[J]. Statistics & Probability Letters,2004,70(3):191-197. [5] Kim T S, Ko M H. Complete moment convergence of moving average processes under dependence assumptions[J]. Statistics & Probability Letters,2008,78(7):839-846. [6] 王定成,赵武.NA序列部分和的矩完全收敛性[J].高校应用数学学报:A辑,2006,21(4):445-450. [7] 陈平炎,柳向东.同分布ρ混合序列的矩完全收敛性[J].数学学报,2008,51(2):281-290. [8] 傅可昂.正相伴序列的矩完全收敛性[J].云南大学学报:自然科学版,2011,33(1):6-10. [9] Lehmann E L. Some concepts of dependence [J].The Annals of Mathematical Statistics,1966,37(5):1137-1153. [10] 黄海午,吴群英,崔昊英,等.两两PQD序列的完全收敛性和强大数定律[J].大学数学,2009,25(3):60-64. [11] 吴群英.混合序列的概率极限理论[M].北京:科学出版社,2006. CompleteMomentConvergenceofPairwisePQDSequences SHEN Jianwei (School of Science, Zhejiang University of Science and Technology, Hangzhou 310023, China) pairwise PQD sequences; complete convergence; complete moment convergence 2012-12-19 沈建伟(1972—),男,讲师,硕士,主要从事概率极限理论研究.E-mail:mysuccess123@163.com 10.3969/j.issn.1674-232X.2013.04.012 O211.4MSC201060F15 A 1674-232X(2013)04-0343-04
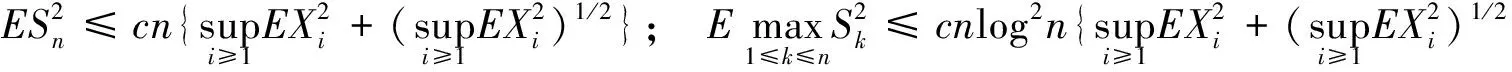
1 主要结果


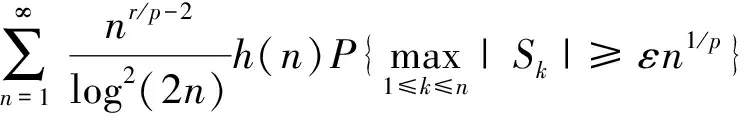
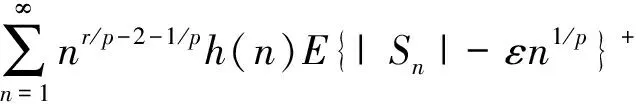
2 定理的证明