一类过山气流背风波问题解法探析

张 瑰,崔周进,张 梅,毛 磊

(1.解放军理工大学理学院，江苏 南京 211101;2.热带海洋环境国家重点实验室(中国科学院南海海洋研究所),广东 广州 510301;3. 南京农业大学理学院，江苏 南京 210095)

一类过山气流背风波问题解法探析

张 瑰1,2,崔周进1,张 梅3,毛 磊1

(1.解放军理工大学理学院，江苏 南京 211101;2.热带海洋环境国家重点实验室(中国科学院南海海洋研究所),广东 广州 510301;3. 南京农业大学理学院，江苏 南京 210095)

研究一类过山气流的背风波问题中产生的二阶变系数微分方程，对几种解法，如积分方程解法、幂级数求解法、构造特解法以及降阶法等，进行简要分析和评述.

二阶微分方程；变系数；幂级数；特解；降阶法

0 引 言

二阶线性微分方程在微分理论中占有重要位置，在科学研究、工程技术中有着广泛应用，其中很多应用类型的问题都可归结为二阶变系数线性常微分方程的求解问题，如贝塞尔方程、勒让德方程、切比雪夫方程等.在经典的气象和流体力学问题——过山气流的背风波问题中，通常会遇到如下一类偏微分方程[1]：

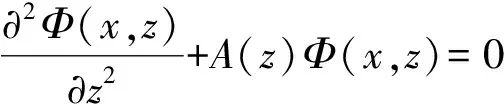
其中，A(z)为已知函数，Φ(x,z)为所求.由于本文仅从理论上探析其解法，为简单起见，文中仅考虑方程本身，定解条件(边界条件或初始条件)暂不予考虑.

采用分离变量法，令Φ(x,z)=f(x)g(z)，或者按照大气科学中常用的波解形式Φ(x,z)=g(z)eikx进行求解，可以将原问题化为如下的二阶常微分方程：

(1)

由于系数A(z)为函数，这给求解g(z)带来了困难.如何求解问题(1)，下面介绍几种方法，并对其进行简要分析和评述.

1 积分方程解法

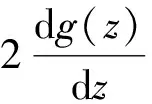
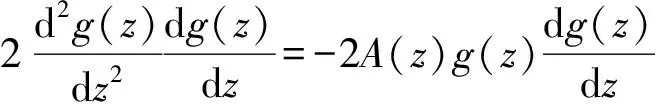
(2)

对z求积，得

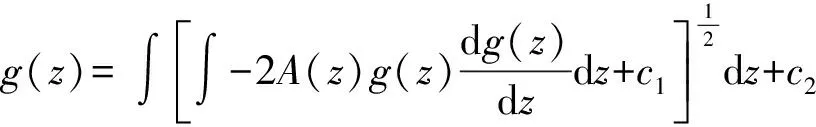
(3)

其中，常数c1，c2由定解条件来确定.

式(3)给出了求解g(z)的一个解析表达式，这是一个非线性不适定的积分方程，它的求解本身就是一个非常困难的问题[2].因此，从理论上讲，对于方程(1)，我们采用积分方程方法求解，所得到的解看似很“完美”，但要在方程(3)中真正解出g(z)，只能运用近似方法，如Tikhonov正则化方法、最大熵方法、有限维逼近法以及非线性迭代法等，在实际应用中存在局限性.

2 幂级数解法

采用幂级数解法[3]的理论依据是：如果A(z)在点z0领域内解析，即它可展成z-z0的幂级数，则方程(1)的解在z0领域内也能展成z-z0的幂级数.

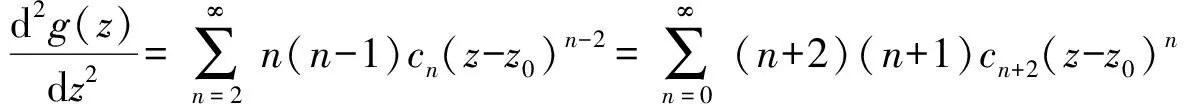
则

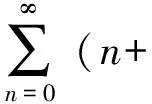
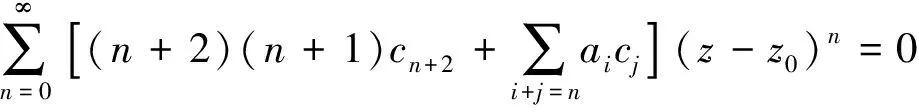
比较同次幂的系数，有

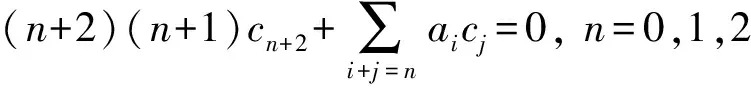
(4)

由于an已知，在实际操作中，可以借助于编程或者相应数学软件(如Matlab)，对式(4)进行求解即可得到cn,于是可得到原方程的解.这种方法看上去繁琐，但借助于计算机运算，可行性与适用性很强.对于一般的二阶方程:

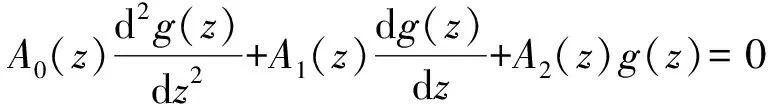
这种方法仍然有效.

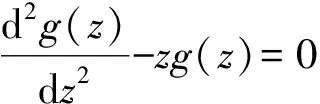
代入原方程，有

[2c2+3·2c3z+…+(n+2)(n+1)cn+2zn+…]-z[c0+c1z+c2z2+…]≡0.

比较上述等式两端的z的同次幂的系数，有

2c2=0,3·2c3-c0=0,…，(n+2)(n+1)cn+2-cn-1=0,….

从而,可得递推关系式

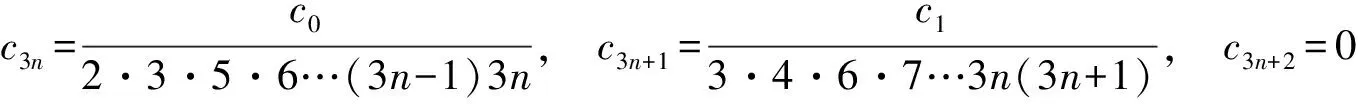
因而

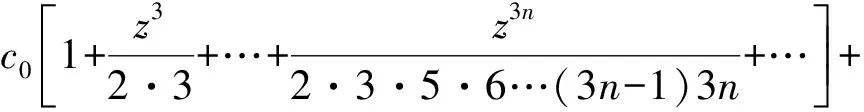
其中,c0,c1为任意常数.如果给定定解条件g(0)=1,g′(0)=2可得c0=1,c1=2.

由于此幂级数的收敛半径无限大，因而级数的和便是所求的特解.解毕.

注1借助于Maple软件，输入如下命令，可以得到例1方程的显式解.

凤河支流官沟流经东半壁店小流域，是流域内主要河流，流域排水一部分通过农田二支渠、三支渠等农田灌溉和排涝渠系排入官沟后入凤河，部分排水直接排入凤河，部分雨水也排入流域坑塘。

eq:=diff(g(z),z$2)-z·g(z)=0

dsolve(eq,g(z));

可得方程的显式解为g(z)=_C1AiryAi(z)+_C2AiryBi(z).

利用幂级数解法对此问题进行求解,结果与特征值方法相吻合,解略.

注2借助于Maple软件，输入如下命令，可以得到例2方程的显式解.

eq:=diff(g(z),z$2)-g(z)=0

dsolve(eq,g(z));

可得方程的显式解为g(z)=_C1e-z+_C2ez.

3 构造特解法

如果已知方程(1)的一个非零特解为g1(z)，则可求出另一个特解

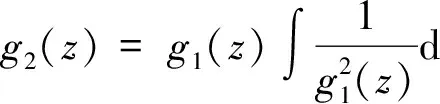
因此关键问题就是如何求解特解g1(z)，我们可以按照第2节中的幂级数方法求特解，也可以用其他的方法，因此这种方法具有一定的灵活性和技巧性.对于一些特殊的方程，它也不失为一种好方法，例如例2中，易得g1(z)=ez是原方程的一个特解，那么另一个特解

所以原方程的通解g(z)=c1ez+c2e-z.

4 降阶法

这种方法的思路是：通过变量代换，将二阶微分方程化为一阶微分方程组[4].

(5)

解方阵的行列式为

W(z)=detx(z)，

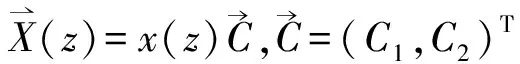
除上文提及的方法之外，还可以利用其他的方法对方程进行求解，如二阶变系数线性常微分方程的常系数化法、数值方法等等，在本文中不予累述.

最后需要强调一点的是，Liouville证明了Riccati方程的解不能用初等函数及其有限次积分求解，也就证明了二阶变系数线性微分方程不能用初等方法求解.实际上，对于一般的二阶变系数线性微分方程

y″+p(x)y′+q(x)y=0，

(6)

令u=y′/y，则y′=yu，y″=yu2+yu′，将其代入上式可得

yu2+yu′+p(x)yu+q(x)y=0，

也即

u′+u2+p(x)u+q(x)=0.

(7)

所以，求解二阶变系数线性微分方程(6)的问题本质上与求解Riccati方程(7)的问题是一致的[6].

[1] 臧增亮,张铭,张瑰.三维三层背风波的理论和数值研究[J].大气科学，2007，31(3)：547-552.

[2] 张瑰，黄思训.非线性不适定问题一种双循环的牛顿型迭代格式[J].数学年刊:A辑,2003，24(3)：321-330.

[3] 东北师范大学数学系.常微分方程[M].北京：人民教育出版社，1983.

[4] 数学手册编写组.数学手册[M].北京：高等教育出版社，1979.

[5] 黄思训,伍荣生.大气科学中的数学物理问题[M].北京：气象出版社，2001：18-26.

[6] 金福临,李训经.常微分方程[M].上海：上海科学技术出版社，1984.

SolutionstotheProblemfortheLeeWaveofAirFlowoverTerrain

ZHANG Gui1,2, CUI Zhoujin1, ZHANG Mei3, MAO Lei1

(1.Institute of Science, PLA University of Science and Technology, Nanjing 211101, China;2.State Key Laboratory of Tropical Oceanography (South China Sea Institute of Oceanology Chinese Academy of Sciences), Guangzhou 510301, China;3.Institute of Science, Nanjing Agricultural University, Nanjing 210095, China)

This paper studied the second-order differential equations with variable coefficients generated from the lee wave of air flow over terrain, analyzed and commented on several solving methods, such as integral equation method, power series method, special solution constructive method and reduced-order method.

second-order differential equations; variable coefficients; power series; special solution; reduced-order method

崔周进(1982—)，男，讲师，硕士，主要从事非线性微分方程理论与应用研究.E-mail:cuizhoujin@126.com

10.3969/j.issn.1674-232X.2013.04.008

O175.1MSC201034A30

A

1674-232X(2013)04-0323-04