Theoretical Studies on NLO Properties of (C9H8N6O2)n (n=1,2,3,4)
2013-10-28GUFenglongTIANSiPENGLiang
GU Fenglong, TIAN Si, PENG Liang
(Key Laboratory of Theoretical Chemistry of Environment, Ministry of Education; School of Chemistry and Environment, South China Normal University, Guangzhou 510006, China)
TheoreticalStudiesonNLOPropertiesof(C9H8N6O2)n(n=1,2,3,4)
GU Fenglong*, TIAN Si, PENG Liang
(Key Laboratory of Theoretical Chemistry of Environment, Ministry of Education; School of Chemistry and Environment, South China Normal University, Guangzhou 510006, China)
The nonlinear optical (NLO) properties of (C9H8N6O2)n(n=1,2,3,4) have been investigated. The static (hyper)polarizabilities of the systems are evaluated by methods of the Hartree-Fock (HF), Density Functional Theory (DFT), and Møller-Plesset perturbation theory at the second order (MP2) with 6-31G**basis set. The structures are optimized at B3LYP/6-31G**level. There are three types of hydrogen bonds, N—H…O—C—C, N…H—N, and N—H…O—C—N, and their lengths are in average 0.196 3, 0.191 8 and 0.190 9 nm, respectively. At the HF/6-31G**level, the first hyperpolarizability (β0) is increased due to more and more hydrogen bond interactions involved asnis increased, i.e.β0is 246, 596, 1 067, or 1 555 (a.u.) forn=1, 2, 3, or 4, respectively. The static second hyperpolarizability (γ0) is 1.4, 4.3, 7.8, or 11.5 (in 104a.u.), respectively, forn=1, 2, 3, or 4. The results show that Δγforn=2, 3 or 4 is 14 768, 35 627 or 58 670 a.u., which keeps increasing due to the interaction of more hydrogen bonds asngrows. Since Δγhas an obvious increase, it is attributed to the cooperativity of hydrogen bonds. The investigation shows that hydrogen bond is an effective factor to design new NLO materials.
Keywords: NLO; hydrogen bond; cooperativity; (C9H8N6O2)n(n=1,2,3,4)
There is an increasing interest in nonlinear optical (NLO) materials due to their potential application in technologies such as telecommunications, information processing, surgery, metallurgy and holography.π-conjugated organic polymers are excellent options because they are easily synthesized and chemically modified, have extremely fast switching times, and resist to high intensity radiation[1]. Besides, supramolecular self-assembly has been a hot area of research for several years, it greatly promotes the development of information, energy, life, environmental and material science disciplines[2]. Multiple-hydrogen-bonded interaction is an important way to form supramolecular polymers[3]. Non-covalent bonds with intermolecular interaction and transport processes are the remarkable features of the weakly bonded systems. In association with organized polymolecular assemblies, functional supermolecules capable of displaying processes of highest efficiency and selectivity may lead to the development of molecular and nanoscale optic-electronic devices, such as high-tech sensor, devices for drug delivery and data storage[4].
Perez and Dupuis[5]studied the urea system and found that the additivity relationship holds well for polarizability (α) and the second order hyperpolarizability (γ) even though some individual components are enhanced significantly in the clusters, while other components show the effect of destructive interference from the neighboring units. The results suggest that the effects of the hydrogen bonds on the (hyper)polarizabilities of the urea crystal may not be as significant as previously thought. Their study raises the question of whether hydrogen bonds of other systems have an significant influence on the (hyper)polarizabilities.
Because hydrogen bonding is a weak interaction, it might need multiple and strong hydrogen bonds to better investigate the hydrogen-bonded system. In Nair and Breedveld’s work[6-7], self-assembly recognition pairs were studied in the six-point hydrogen bonded complex between the Hamilton wedge acceptor and cyanuric acid and the three-point hydrogen bonded complex between 2,4-diaminotriazine and cyanuric acid. Inspired by those work, we designed a new molecular system (Figure 1), 6,8-diamino- 4,9-dihydro-2,4,7,9-tetraaza-fluorene-1,3-dione (C9H8N6O2), to study the hydrogen bond cooperativity and NLO properties. C9H8N6O2is aπ-conjugated system and it can form dimer, trimer, and so on, with multiple hydrogen bonds.
In this paper, we sought to know whether the hydrogen-bond network favors or destroys the optical response of the systems, whether there is hydrogen bond cooperativity and to what extent it affects the NLO properties of the systems.
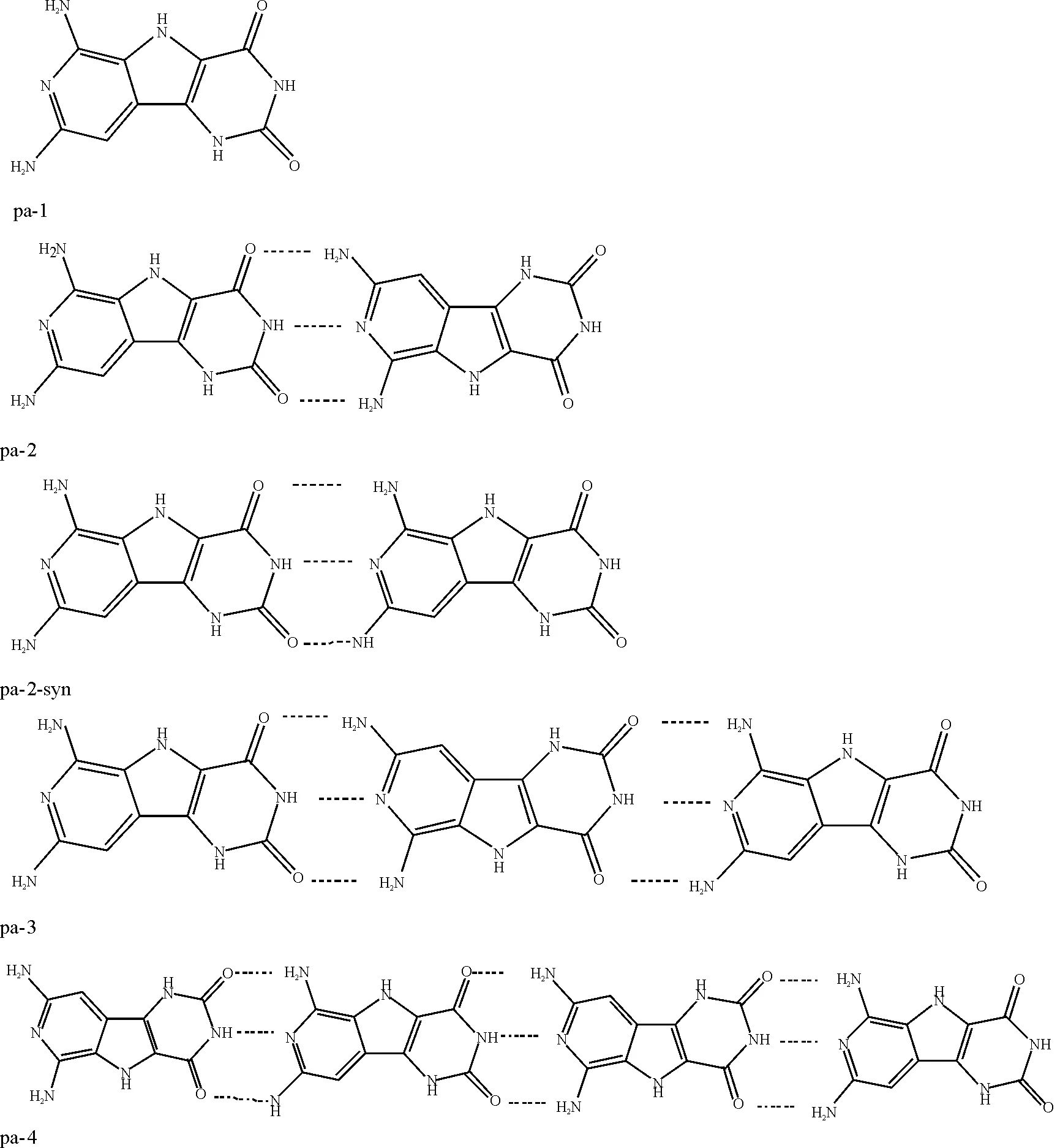
Figure 1 Structures of the systems, 6,8-diamino- 4,9-dihydro-2,4,7,9-tetraaza-fluorene-1,3-dione (C9H8N6O2): monomer (pa-1), synclastic dimer (pa-2-syn), aligned dimer (pa-2), trimer (pa-3) and tetramer (pa- 4)
1 Methodology
The complex (C9H8N6O2)nis denoted as pa-1, pa-2, pa-3 or pa- 4 forn=1, 2, 3 or 4, respectively. The center of mass of the compound was chosen as the origin of the Cartesian coordinate system, aligned along thex-axis. All the geometries of the systems were optimized by using B3LYP/6-31G**. NLO components of pa-2 were calculated and at B3LYP, HF and MP2 levels with a series of basis sets to investigate the basis set effect and the choice of a proper method. The polarizability and first hyperpolarizability were evaluated by analytical means, while the second hyperpolarizability was evaluated by the Finite Field (FF) approach.
The total energy of a molecular system in the presence of a homogeneous electric field can be expressed as follows:

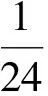
(1)
whereE0is the total energy without the electric field, andFiis the electric field component along theidirection.μi,αij,βijk,γijklare the dipole, polarizability, the first hyperpolarizability and second hyperpolarizability, respectively.
The dipole moment (μ0) and polarizability (α0) are defined as follows:
(2)
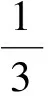
(3)
The static first hyperpolarizability is denoted as:
(4)
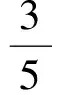
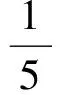
(5)
As to our system, the repeated unit is the same moleculeA(Astands for C9H8N6O2), so the interaction energy of the system (An) is defined as:
ΔEAn=EAn-nEA.
(6)
All the results were corrected for the basis set superposition error (BSSE) using the counterpoise correction by Boys and Bernardi. In the paper, the increase of NLO component is defined:
ΔPAn=PAn-nPA,
(7)
whereP=μ,α,β,γ[8-9].
The increase of NLO component and the ratio of the increase (ΔPAn/PAn) are examined.
All calculations were carried out using the Gaussian 03W package.
2 Results and discussion
2.1 Structure optimization and analysis
All the geometries of the systems were optimized at B3LYP/6-31G**level and the optimized structures are with all real frequencies. The structures are shown in Figure 1. As for the dimer, two structures were designed, one is that the two N atoms in two different five-atom rings are on the same side, that is the two N atoms being synclastic, denoted as pa-2-syn; the other one is that the two N atoms are on the opposite sides, denoted as pa-2.
The energy of pa-1 is -826.818 0 a.u. and that of pa-2 is -1 653.657 8 a.u. For pa-2-syn, it is -1 653.657 3a.u.. The energy of hydrogen bond is -74.73 kJ/mol or -75.80 kJ/mol for pa-2 or pa-2-syn, respectively. The statistics show that pa-2 is a little bit more stable than pa-2-syn and the hydrogen bonds in the system are strong. Besides, in the optimized structures of the two dimer structures, pa-2 is more kept in alignment than pa-2-syn due to the hydrogen bonds. Therefore, pa-2 model is chosen for further investigations. So we can better estimate the cooperativity of hydrogen bond interaction along the direction and its influence on the NLO properties along this direction. That is to say, the model that the two N atoms in two different five-atom rings were put on the opposite sides was chosen for further investigation, keeping the systems more in alignment, asngrows. While pa-2-syn is used only for the purpose of comparison. However, as to pa-2-syn model, asngrows, the system may form a ring, like (CH3—C≡N)n[10]or helix structure like DNA bases. This might need future investigation.
There are three hydrogen bonds between two adjacent subunits in the system. Hydrogen bond lengths and angles are listed in Table 1. The hydrogen bond lengths of N—H…O—C—C, N…H—N, and N—H…O—C—N in systems are in average 0.196 3, 0.191 8 and 0.190 9 nm, respectively. While in pa-2-syn, they are about 0.190 8, 0.195 6 and 0.194 0 nm, respectively. The angles are very close to a flat angle, which makes the system almost alignment. The results show that there are strong hydrogen bonds in these systems.
NBO analysis was done at B3LYP/6-31G**level. In pa-2, the charge of the first unit is 0.006 06, of the second unit is -0.006 06. For pa-2-syn, the charge of the first unit is 0.012 87 and of the second is -0.012 87. As to pa-3, the charges of the first, second and the third unit are 0.008 63, -0.000 10 and -0.008 52, respectively. For pa- 4, they are 0.009 02, 0.001 51, -0.001 37 and -0.009 15, respectively.
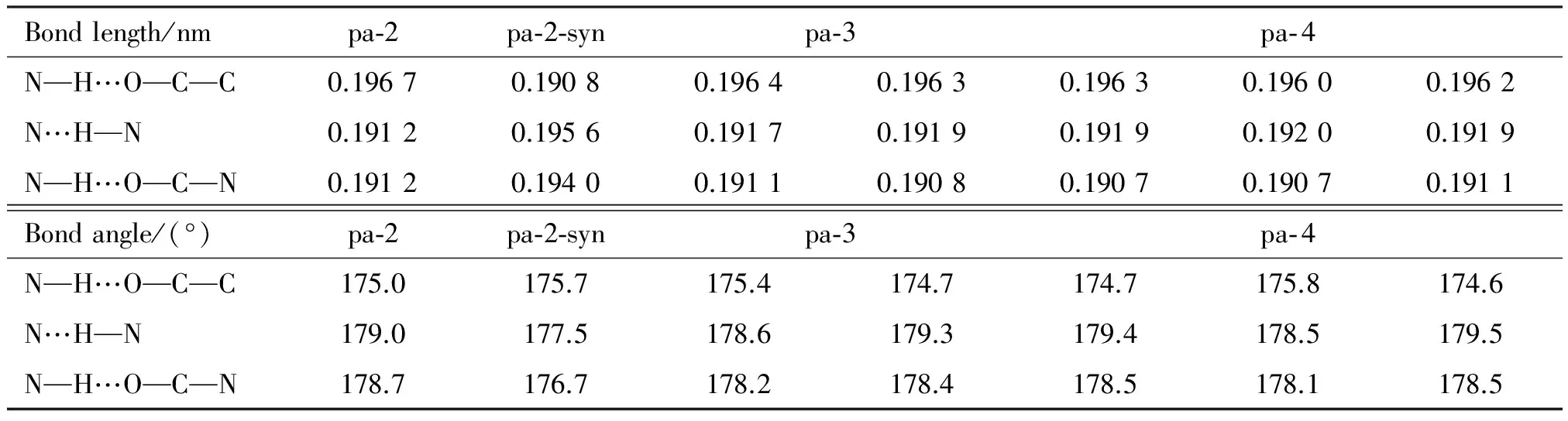
Table 1 Hydrogen bond lengths and hydrogen bond angles of the systems (at B3LYP/6-31G** level)
2.2 Basis set effect on NLO
The NLO properties of the systems were calculated at HF/6-31G**level. And the results with and without BSSE corrections using the counterpoise correction by BOYS and BERNARDI[8]were compared. It is demonstrated in Table 2 that the values ofμ0,α0,β0differ slightly from those with BSSE correction, the largest difference is 2.38%. So the BSSE correction can be neglected and the following results presented are without BSSE correction.
Table 2 Non-corrected and BSSE counterpoise-corrected (in parentheses) NLO components (a.u.) of the system at HF/6-31G**level

pa⁃2pa⁃2⁃synpa⁃3pa⁃4μ03.89(3.86)4.07(4.03)6.03(5.95)8.16(8.04)α0273.60(270.96)273.32(270.68)419.42(414.13)566.11(558.17)β0596.36(584.42)636.21(627.13)1067.24(1043.39)1555.49(1519.38)
pa-2 was calculated at HF level with a series of basis sets to investigate their effects on NLO properties. The results are shown in Table 3 in the order of number of basis function (N) increased. As N increases, the total dipole momentμ0and the total mean polarizabilityα0change slightly with different basis sets. The mean first hyperpolarizabilityβ0, however, decreases when diffuse function or polarized function is employed. Besides,β0has a value of 585 using DGDZVP basis set with 508 functions, while it has a value of 506 a.u. by the largest basis set cc-pVQZ with 2 350 functions being tested in this work. 6-31G**was chosen for further NLO studies duo to its reliability and time efficiency.
All values reported in a.u.
Besides,β0of pa-2 was calculated at B3LYP, HF and MP2 levels with a series of Pople basis sets. The results are shown in Figure 2.β0has a maximum value for 6-31G and starts to converge from 6-31G**at all three levels. Andβ0at B3LYP and MP2 levels are close to each other because both methods take electron correlation into account, whereas HF level is about 45% lower than either of them since the electron correlation effects are not considered at the HF level. However, as n or the number of atoms in the system grows, it will require much more computational costs, especially for MP2. Besides that, DFT method confronts difficulties in the treatment of NLO properties for longer chain systems. It has been noticed that conventional DFT significantly overestimates polarizability (α) and hyperpolarizability (γ) and gives catastrophically divergent values for long chain lengths[11-12]. Thus, HF method has been used for further NLO calculations.

Table 3 (Hyper)polarizabilities of pa-2: Basis set dependence

Figure 2 β0 (a.u.) of pa-2 at B3LYP, MP2 levels and β0 of (C9H8N6O2)n(n=1, 2, 3 and 4) at HF level with different basis sets
Based on these results, HF level with 6-31G**is chosen for following NLO calculations.
2.3 NLO properties of (C9H8N6O2)n(n=1,2,3,4) at HF level
(C9H8N6O2)n(n=1, 2, 3 or 4) were calculated at HF level with different Pople basis sets, theβ0results are also shown in Figure 2.β0has an obvious increase asngets bigger. The increase ratio of adding one subunit is about 60%, 43% and 31%, forn=2, 3, and 4, respectively, whatever the considered basis set is. The Finite-Field approach was employed to calculate the second order hyperpolarizabilityγ0, the results are listed in Table 4.
From Table 4, one can see that theβXXXandγXXXXcomponents have the largest value, they are the most important contributions toβ0andγ0. And the major charge transfer is also along thexdirection.μ0,α0,β0andγ0all have an obvious increase asngrows.β0is 246, 596, 1 067 or 1 555 (a.u.), andγ0is 14 169, 43 106, 78 134 or 115 346 (a.u.), for the monomer, dimer, trimer, or tetramer, respectively. In Perez and Dupuis’s work[5],γ0is 404×10-39esu (802 a.u.), 805×10-39esu (1 598 a.u.) or 1 202×10-39esu (2 386 a.u.) for urea monomer, linear dimer or linear trimer, respectively. It is shown that our system is a potentially good NLO material compared to urea systems.
Besides, pa-2-syn has biggerβ0value but lowerγ0value than pa-2. This may be because pa-2-vsyn has different structure and charge transfer liability.
The change of the NLO properties (ΔP) and their change ratios (ΔP/P) are listed in Table 5. The change ratios of Δβ0are 17.50%, 30.85% and 36.74% whenn=2, 3 and 4, respectively. And they are 34.26%, 45.60% and 50.86%, respectively for Δγ. It is demonstrated in Table 5 that all the ratios accelerate as the system grows, which means more hydrogen bonds. So it is shown that the cooperativity of hydrogen bond interactions among adjacent subunits in the system have a significant influence on the NLO properties. And this system may be considered for new NLO material design.
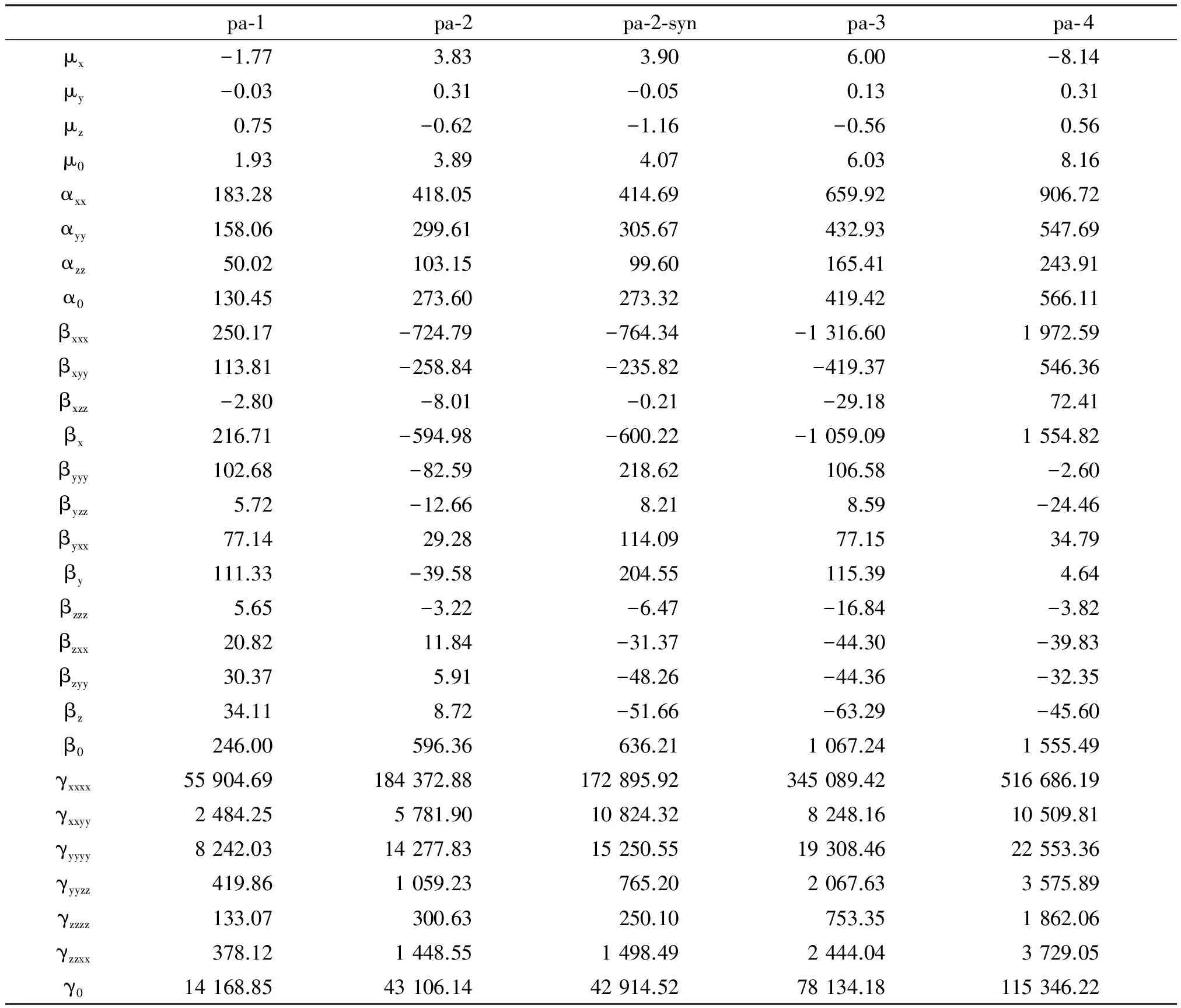
Table 4 Electric properties of the title system at HF/6-31G** level

Table 5 Differences of electric properties and percent deviation from additivity of (C9H8N6O2)n (n= 1, 2, 3 or 4)
All values in a.u.
Sadlej pVTZ is known as one of the best basis sets for electric property calculations. But due to our computer capacity, we only performed calculations with Sadlej pVTZ basis set for pa-1 and compared with those of HF/6-31G**, the results are listed in Table 6.μ0is about 1.93 a.u. which is almost the same as that of HF/6-31G**, whileα0,αxx,αyyandαzzwith Sadlej pVTZ are all larger than those with 6-31G**. However,βx,βyandβzare smaller:β0with Sadlej pVTZ is 184 a.u. while with 6-31G**it is 246 a.u.
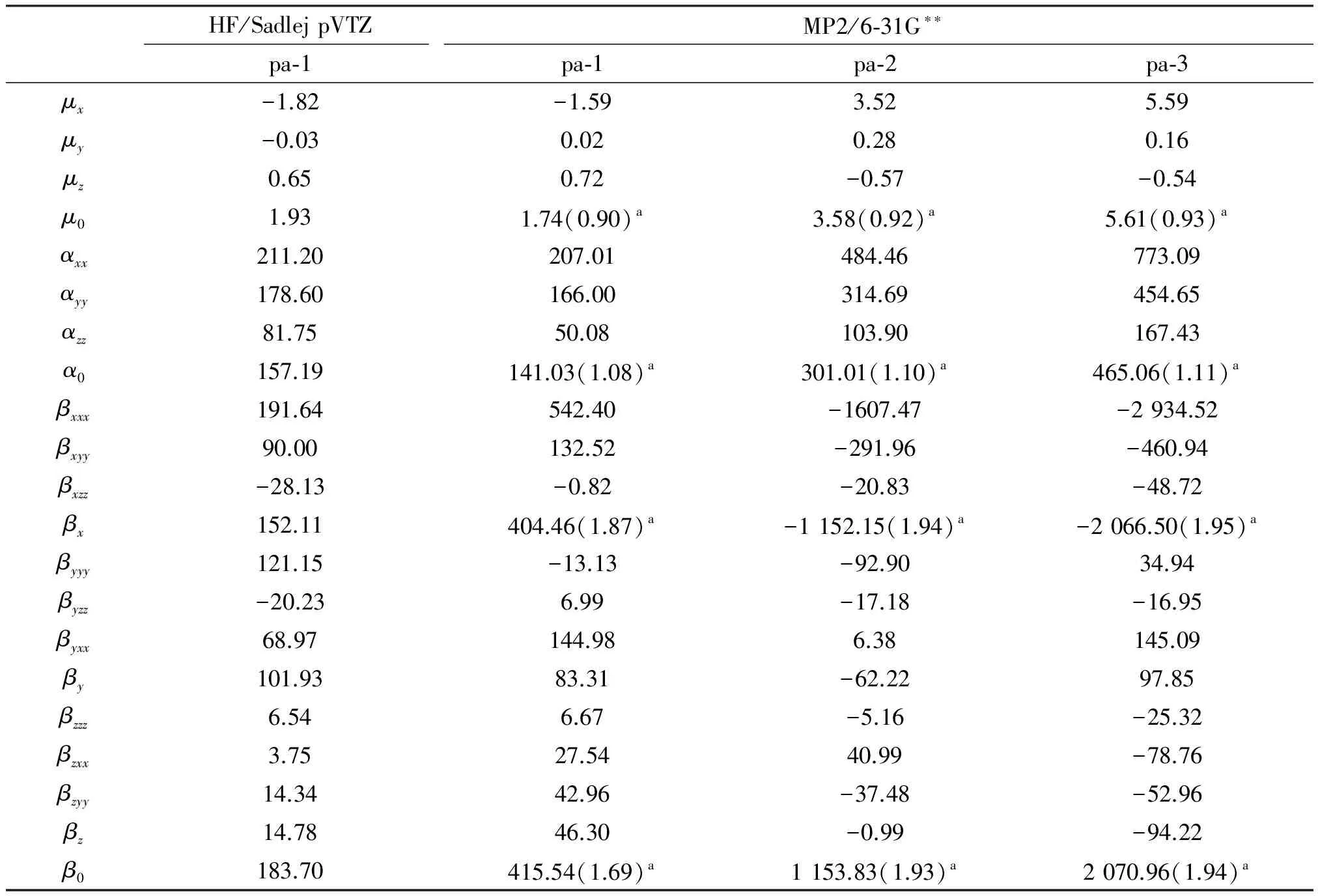
Table 6 Electric properties of (C9H8N6O2)n (n= 1, 2, 3 or 4) at HF/Sadlej pVTZ and MP2/6-31G** level
aValue in parentheses is the ratio of MP2 to HF
Besides, MP2 calculations of the system were compared with HF ones, and the results are listed in Table 6. The ratio of MP2 to HF is about 0.9, 1.1 and 1.9, respectively, whenn=1, 2 and 3. This can be used to estimate the electron correlation effects on the NLO components of the system if a comparison to the experimental results is made.
3 Conclusions
The NLO properties of hydrogen-bonded(C9H8N6O2)n(n=1, 2, 3 or 4) were investigated and the relationship of the values and the structure of the system was compared. All the geometries of the systems were optimized using B3LYP/6-31G**. The structures are mainly determined by the hydrogen bond interactions. Three kinds of hydrogen bond distances are in average 0.196 3, 0.191 8 and 0.190 9 nm. The hydrogen bonds are strong. The total charge transfers are 0.006 1, 0.008 6, and 0.010 5 (a.u.) for pa-2, pa-3 and pa- 4, respectively.
NLO calculations show that the increasing ratios of Δβ0are 17.50%, 30.85% and 36.74% whenn=2, 3 and 4, respectively. And they are 34.26%, 45.60% and 50.86%, respectively, for Δγ. In our system, the cooperativity of hydrogen bond has a significant influence on the NLO properties. So the hydrogen bond system is a potential structure for designing future NLO materials.
[1] TORRENT-SUCARRAT M, SOLA M, DURAN M, et al. Basis set and electron correlation effects on ab initio electronic and vibrational nonlinear optical properties of conjugated organic molecules[J]. J Chem Phys, 2003, 118: 711-718.
[2] GAO Z H, MA T F, DU Z Q, et al. Superamolecular self-assembly and its application in the field of polymer synthesis[J]. Appl Chem Industry, 2012, 41: 1060-1063.
[3] WANG Y J, TANG L M. Supramolecular polymers formed through hydrogen-bonded noncovalent interactions[J]. Process Chem, 2006, 18(0203): 308-315.
[4] POMOGAEVA A, GU F L, IMAMURA A,et al. Electronic structures and nonlinear optical properties of supramolecular associations of benzo-2,1,3-chalcogendiazoles by the elongation method[J]. Theor Chem Acc, 2010, 125: 453-460.
[5] PEREZ J, DUPUIS M. Hydrogen Bonds and (hyper)polarizabilities in Molecular Crystals: An ab initio SCF study of Urea[J]. J Phys Chem, 1991, 95(17): 6525-6529.
[6] NAIR K P, BREEDVELD V, WECK M. Complementary hydrogen-bonded thermoreversible polymer networks with tunable properties[J]. Macromolecules, 2008, 41(10): 3429-3438.
[7] NAIR K P, BREEDVELD V, WECK M. Modulating mechanical properties of self-assembled polymer networks by multi-functional complementary hydrogen bonding[J]. Soft Matter, 2011, 7: 553-559.
[8] BOYS S F, BERNARDI F. The calculation of small molecular interactions by the differences of separate total energies: Some procedures with reduced errors[J]. Mol Phys, 1970, 19(14): 553-566.
[9] BARANOWSKA A, FERNANDEZ B, SADLEJ A J. Importance of electron correlation effects and basis set superposition error in calculations of interaction energies and interaction-induced electric properties in hydrogen-bonded complexes: A model study[J]. Theor Chem Acc, 2011, 128: 555-561.
[10] KHARAT B, DESHMUKH V, CHAUDHARI A. Computational study of (CH3—C≡N)n(n=1-5) oligomers using Density Functional Theory method[J]. J Mol Liq, 2013, 177: 172-181.
[11] SEKINO H, MAEDA Y, KAMIYA M, et al. Polarizability and second hyperpolarizability evaluation of long molecules by the density functional theory with long-range correction[J]. J Chem Phys, 2007, 126: 014107.
[12] SONG J W, WATSON M A, SEKINO H, et al. Nonlinear optical property calculations of polyynes with long-range corrected hybrid exchange-correlation functional[J]. J Chem Phys, 2008, 129: 024117.
2013-02-30
国家自然科学基金项目(21073067)
1000-5463(2013)06-0105-08
O6-04
A
10.6054/j.jscnun.2013.09.013
(C9H8N6O2)n(n=1,2,3,4)分子体系非线性光学的理论研究
顾凤龙*, 田 思, 彭 亮
(环境理论化学省部共建教育部重点实验室,华南师范大学化学与环境学院, 广东广州 510006)
该文研究了(C9H8N6O2)n(n=1,2,3,4)分子体系的非线性光学性质, 采用Hartree-Fock方法、密度泛函方法以及Møller-Plesset微扰理论方法在6-31G**基组下分别计算了该体系的静电场超极化率. 其几何结构在B3LYP/6-31G**条件下进行了优化,发现它们有3种不同的氢键形式,其键长分别为0.196 3,0.191 8,0.190 9 nm. 在HF/6-31G**水平下,发现一级超极化率(β0)的增长是由于随着n的增大,体系的氢键数目增加造成的,当n=1,2,3,4时,它们β0的值分别为246,596,1 067,1 555 (原子单位),当n=1,2,3,4时,它们的二级超极化率(γ0)的值分别为1.4,4.3,7.8,11.5 (104原子单位). 结果显示随着n的增大,体系氢键数目的增加、相互作用的增强,Δγ也随着增大,在n=2,3,4时分别为14 768,35 627,58 670 (原子单位). 该研究显示氢键是设计非线性光学材料的关键因素.
非线性光学; 氢键; 协同作用; (C9H8N6O2)n(n=1,2,3,4)
*通讯作者:顾凤龙,教授,珠江学者,Email: gu@scnu.edu.cn.
【中文责编:成文 英文责编:李海航】
