一类奇异摄动对流扩散方程组的自适应移动网格方法
2013-10-28陈艳萍刘利斌
陈艳萍, 刘利斌
(华南师范大学数学科学学院,广东广州 510631)
一类奇异摄动对流扩散方程组的自适应移动网格方法
陈艳萍*, 刘利斌
(华南师范大学数学科学学院,广东广州 510631)
针对一类奇异摄动对流扩散方程组问题,利用有限差分方法,提出了求解这类问题的自适应移动网格方法,并给出了移动网格的迭代算法和一阶后验误差估计.数值实验验证了所得的理论估计.
对流扩散方程组; 移动网格; 奇异摄动
奇异摄动问题起源于工程和应用数学的多个分支,包括流体力学、量子力学、弹性力学、化学反应器和最优控制等.这类问题的特点是在讨论的微分方程中含有扰动参数,该参数可以反映一定的物理性质,也可以人为地改进.这类问题的解在求解区域的局部范围内变化非常剧烈.对于这类问题的数值方法,在均匀网格上很难得到理想的数值解.这就要求寻找一种非均匀网格,在解发生剧烈变化的局部范围内加密剖分,以适应问题的奇异扰动特性.目前主要有2种非均匀网格方法:层适应网格和自适应移动网格方法. 近年来,这2类方法被广泛用于数值求解单个奇异摄动问题[1-6]. 对于含有多个参数的奇异摄动方程组,层适应网格方法的研究成果相对比较多[7-9],而自适应网格方法的研究成果很少.
本文将考虑如下奇异摄动对流扩散方程组
(1)

1 连续解的稳定性分析
将问题(1)写成如下矩阵形式
(2)
其中
假设β1≥a11(x),β2≥a22(x),且在后面的误差估计中,定义最大值范数和非负范数:
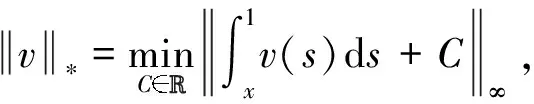
定理1 如果f(x)=-F′(x),则问题(1)存在一个唯一的弱解u(x)=(u1(x),u2(x))T,且有如下的估计
其中C为某个确定的常数.
定理1的证明类似文献[6]的定理3.1.

ui(0)=wi(0),ui(1)=wi(1),Tu(x)-Tw(x)=f(x),
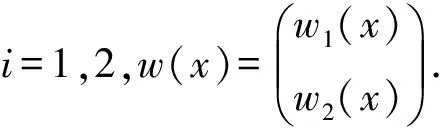
2 离散差分格式与网格等分布
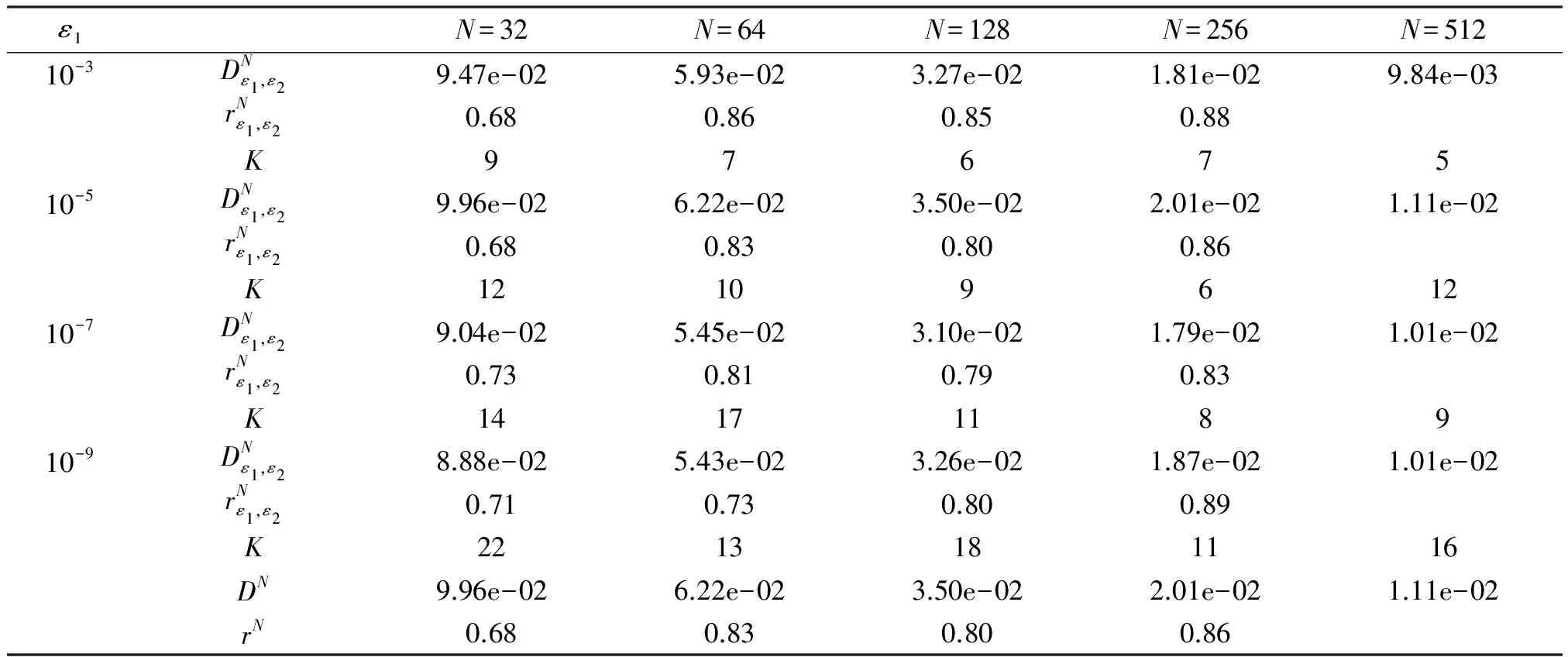
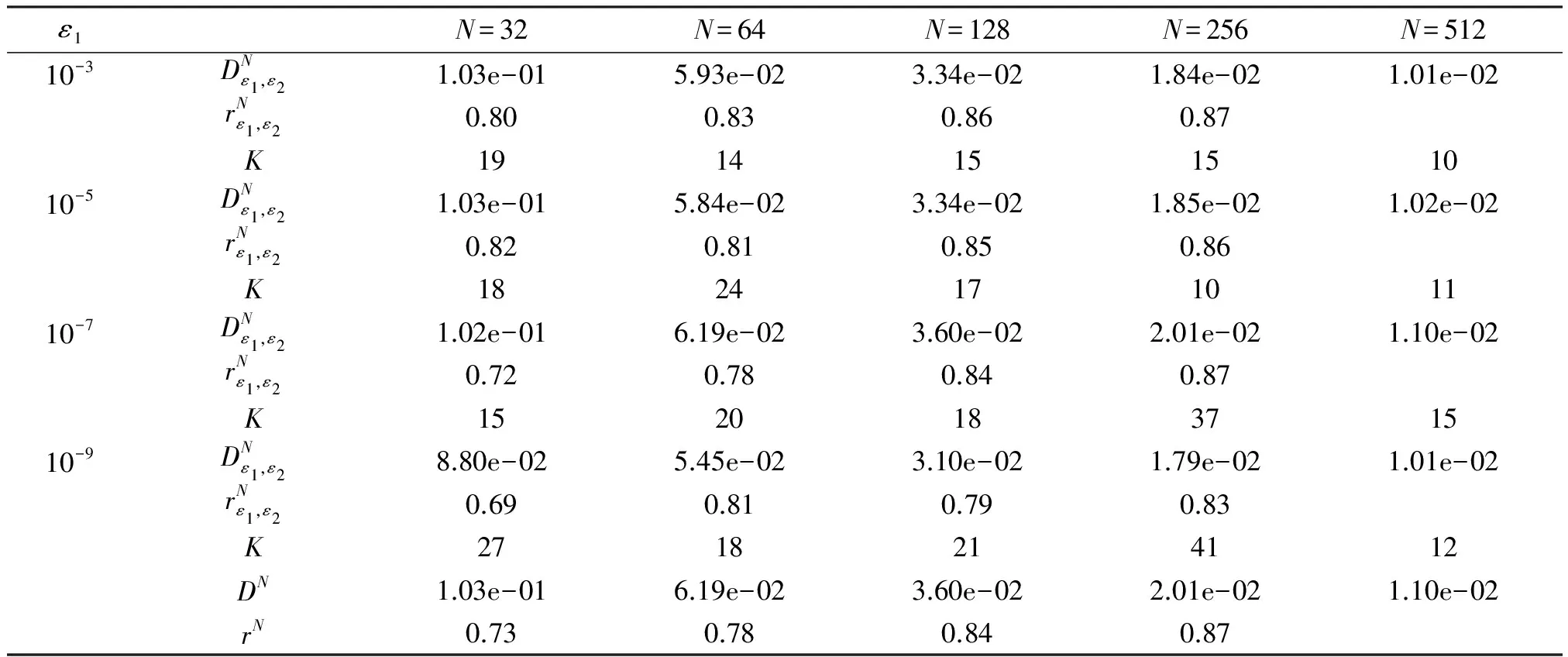
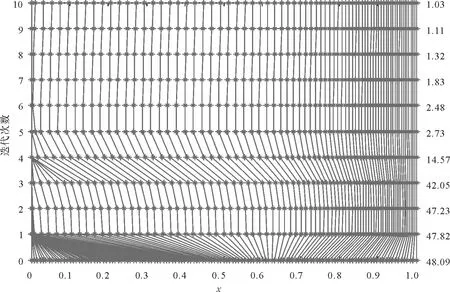
考虑任意网格ΩN={x0,x1,…,xN},其中0=x0 于是,对于问题(1),可构造如下的有限差分格式 (3) 对于单个奇异摄动对流扩散问题,大部分学者采用基于等分布原理的移动网格方法,即选择控制函数M(x),使得 (4) 目前,在实际计算过程当中,通常选择弧长控制函数 其中uN(x)为解的分段连续的线性插值函数. 类似地,对于奇异摄动对流扩散方程组,本文在构造自适应移动网格方法时,选择如下控制函数 (5) 其中j=1,2,…,N-1. 为了数值求解问题(1)和等分布问题(5),我们构造了如下的迭代算法: 第1步:设定初始网格{0,1/N,…,1}为均匀网格. 第3步:网格测试.设C0>1为事先设定的常数.如果 则执行第5步,否则执行第4步. UN(xi-1)=Ui-1,UN(xi)=Ui,(UN(x))″=DD-Ui, (UN(x))′=DD-Ui(x-xi-1/2)+D-Ui, 其中xi-1/2=(xi+xi-1)/2,则 (6) 于是可得: 推论2 令u(x)为问题(1)的精确解,Ui为差分格式(3)的解, 则 定理2 令u(x)为问题(1)的精确解,Ui为差分格式(3)的解,则 定理2的证明类似文献[6]的定理4.1. 考虑如下常系数奇异摄动对流扩散方程组 (7) 为了计算最大误差和收敛阶,首先使用双重网 格原理来估计其误差,具体定义如下 其中UN和U2N分别表示用N和2N个网格区间计算得到的数值结果.然后利用下式来计算收敛阶: 表1~表4列出了取不同的ε1、ε2和N时,利用移动网格方法计算得到的离散最大模误差,同时也给出了相对应的收敛率以及网格迭代次数.从表1~表4的数据可以看出,在最大模误差估计下,这些收敛率随着N的增大而逐步接近1.表明用移动网格方法计算得到的数值解是一致一阶收敛的,且与参数ε1,ε2和N无关.总的来说,我们的数值结果符合前面的理论分析. 另外,在利用本文给出的自适应移动网格方法数值求解奇异摄动对流扩散方程组时,不必事先给出各个摄动参数的大小,而利用层适应网格方法求解这类问题时,必须首先给出摄动参数的大小,具体可见文献[10]. 图1给出了利用移动网格算法求解问题(5)时网格的迭代过程,从底部往上观察,可得到每次迭代后网格点的移动过程.另外,随着迭代次数的增加,C0的值逐渐趋近于1.在本文的计算过程中,取C0=2.最后,由图1可得出结论:在实际计算过程中,C0的值越小,移动网格算法的迭代次数就越多. 表1 最大误差估计和收敛阶(ε2=1)Table 1 Maximum error estimate and convergence order (ε2=1) 表2 最大误差估计和收敛阶(ε2=10-3)Table 2 Maximum error estimate and convergence order (ε2=10-3) 表3 最大误差估计和收敛阶(ε2=10-5)Table 3 Maximum error estimate and convergence order (ε2=10-5) 表4 最大误差估计和收敛阶(ε2=10-7)Table 4 Maximum error estimate and convergence order (ε2=10-7) 图1 网格的移动过程(N=128,ε1=10-8,ε2=10-6) [1] LINSS T, ROOS H G, VULANOVIC R. Uniform point-wise convergence on Shishkin-type meshes for quasi-linear convection-diffusion problems[J]. SIAM J Numer Anal, 2000, 38: 897-912. [2] LIU W B, TANG T. Error analysis for a Galerkin-spectral method with coordinate transformation for solving singularly perturbed problems[J]. Appl Numer Math, 2001, 38: 315-345. [3] KOPTEVA N. Maximum norm a posteriori error estimates for a one dimensional convection-diffusion problem[J]. SIAM J Numer Anal, 2002, 39: 423-441. [4] KOPTEVA N, STYNES M. A robust adaptive method for quasi-linear one-dimensional convection diffusion problem[J]. SIAM J Numer Anal, 2002, 39, 1446-1467. [5] CHEN Y P. Uniform point-wise convergence for a singularly perturbed problem using arc-length equidistribution[J]. J Comput Appl Math, 2003, 159(1): 25-34. [6] CHEN Y P. Uniform convergence analysis of finite difference approximations for singularly perturbation problems on an adaptive grid[J]. Adv Comput Math, 2006, 24: 197-212. [7] MADDEN N, STYNES M. A uniformly convergent numerical method for a coupled system of two singularly perturbed linear reaction-diffusion problems[J]. IMA J Numer Anal, 2003, 23: 627-644. [8] LINß T, MADDEN N. Accurate solution of a system of coupled singularly perturbed reaction-diffusion equations[J]. Computing, 2004, 73: 121-133. [9] LINß T, MADDEN N. Layer-adapted meshes for a linear system of coupled singularly perturbed reaction-diffusion problems[J]. IMA J Numer Anal, 2009, 29: 109-125. [10] BELLEW S, RIORDAN E O. A parameter robust numerical method for a system of two singularly perturbed convection-diffusion equations[J]. Appl Numer Math, 2004, 51: 171-186. Keywords: a system of convection diffusion; moving grid; singularly perturbed AnAdaptiveMovingGridMethodfortheSingularlyPerturbedConvection-DiffusionProblem CHEN Yanping*, LIU Libin (School of Mathematical Sciences, South China Normal University, Guangzhou 510631, China) A singularly of two singularly perturbed convection-diffusion problem is considered. Based on finite difference scheme, an adaptive moving grid approach to solve this problem is presented, and an iteration algorithm to generated meshes and a first-order a posteriori error estimate are given. Numerical results are presented that support our theoretical estimates. 2013-07-08 国家自然科学基金项目(11271145,11301044);国家教育部高等学校博士学科点专项科研基金课题(20114407110009);广东省高等学校高层次人才项目;广东省高等院校学科建设专项资金(第一批)科技创新项目(2012KJCX0036);华南师范大学研究生创新基金(2012kyjj118) *通讯作者:陈艳萍,教授,珠江学者,Email:yanpingchen@scnu.edu.cn. 1000-5463(2013)06-0001-05 J653 A 10.6054/j.jscnun.2013.09.001 【中文责编:庄晓琼 英文责编:肖菁】
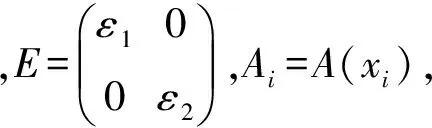

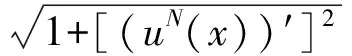
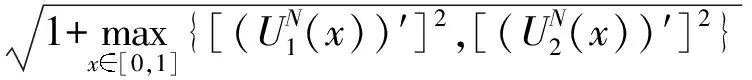
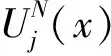
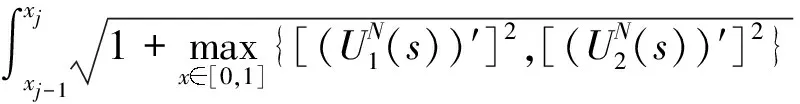

3 移动网格方法
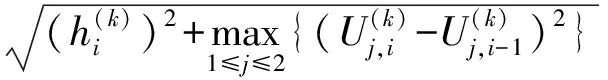

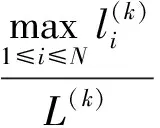
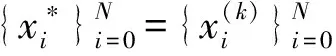
4 后验误差估计


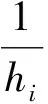
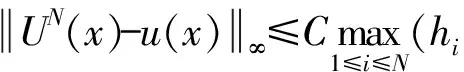
5 数值试验