Very Expressive Intuitionistic Fuzzy Rough Description Logics for the Semantic Web
2013-10-28JIANGYuncheng
JIANG Yuncheng
(School of Computer Science, South China Normal University, Guangzhou 510631, China)
VeryExpressiveIntuitionisticFuzzyRoughDescriptionLogicsfortheSemanticWeb
JIANG Yuncheng*
(School of Computer Science, South China Normal University, Guangzhou 510631, China)
The state-of-the-art and some existing problems of intuitionistic fuzzy rough Description Logics(DLs) for the Semantic Web are analyzed. An integration between the theories of intuitionistic fuzzy DLs and rough DLs, i.e., intuitionistic fuzzy rough DLs, has been provided based on (,)-intuitionistic fuzzy rough set theory. Concretely, the intuitionistic fuzzy rough DLIFRSROIQ(D) is presented, which is the extension of the expressive DLSROIQ(D) behind OWL 2. It is proved that the reasoning tasks (knowledge base satisfiability, concept satisfiability, subsumption, logical consequence, ABox consistency, BTCB, and BSB reasoning) in the intuitionistic fuzzy rough DLIFRSROIQ(D) may be reduced to the corresponding reasoning in the fuzzy DL over complete latticesL*-SROIQ(D), respectively.
Keywords: description logics; fuzzy description logics; rough description logics; (,)-intuitionistic fuzzy rough sets; Semantic Web
In the last years, the use of ontologies as formalisms for knowledge representation in many different application domains has grown significantly[1]. Ontologies have been successfully used as part of expert and multi-agent systems, as well as a core element in the Semantic Web, which proposes to extend the current Web to give information a well-defined meaning[2-3]. An ontology is defined as an explicit and formal specification of a shared conceptualization[4], which means that ontologies represent the concepts and the relationships in a domain promoting interrelation with other models and automatic processing. Ontologies allow to add semantics to data, making knowledge maintenance, information integration as well as the reuse of components easier[1].
The current standard language for ontology creation is the Web Ontology Language (OWL)[1,5], which consists of the three increasingly expressive sublanguages OWL Lite, OWL DL, and OWL Full. OWL Full is the most expressive level but reasoning within it becomes undecidable, OWL Lite has the lowest complexity and OWL DL is a balanced tradeoff between expressiveness and reasoning complexity. However, since its first development, several limitations on expressiveness of OWL have been identified, and consequently several extensions to the language have been proposed[1].
Description Logics (DLs for short)[6]are a family of knowledge representation languages which can be used to represent the terminological knowledge of an application domain in a structured and formally well-understood way. Each logic is denoted by using a string of capital letters which identify the constructors of the logic and therefore its complexity[1]. Important characteristics of DLs are high expressivity together with decidability, which guarantee that reasoning algorithms always terminate with correct answers. Nowadays, DLs have been proved to be very useful as ontology languages. For example, OWL Lite, OWL DL, and OWL 2 have a formal semantics and a reasoning support through a mapping to the expressive DLsSHIF(D),SHOIN(D), andSROIQ(D), respectively[1,5-9]. More precisely, without regarding annotation properties of OWL, the OWL Lite, OWL DL, and OWL 2 are equivalent to DLsSHIF(D),SHOIN(D), andSROIQ(D), respectively.
Nevertheless, it has been widely pointed out that classical DLs[6]are not appropriate to deal with imprecise and vague knowledge, which is inherent to several real world domains[1,10]. The rising popularity of DLs and their use, and the need to deal with uncertainty and vagueness, both especially in the Semantic Web[2-3], is increasingly attracting the attention of many researchers and practitioners towards DLs able to cope with uncertainty and vagueness[11]. Several extensions of DLs have been proposed relying on various extensions of classic logic: there have been probabilistic[12], possibilistic[13], fuzzy[1,14-18], and rough[19-20]extensions that have fundamental differences in terms of semantics and thus in the types of knowledge they model. The probabilistic and possibilistic approaches capture uncertainty and make it possible to represent uncertain knowledge, whereas the fuzzy approach captures vagueness and allows to represent fuzzy knowledge, and the rough approach deal withes rough (or imprecise) knowledge.
Despite the growing popularity of these extended DLs such as probabilistic DLs, possibilistic DLs, fuzzy DLs, and rough DLs, relatively little work has been carried out in integrating them to the management of uncertain and imprecise information, the aim being to develop some new DL theories of uncertainty and vagueness stronger than both of them. At this aspect, we have carried out some works. For instance, we integrated fuzzy DLs (resp., intuitionistic fuzzy DLs) and rough DLs based on fuzzy rough set theory[21-22](resp., intuitionistic fuzzy rough set theory[22-25]), in other words, we presented fuzzy rough DLs[26](resp., intuitionistic fuzzy rough DLs[27]). There also are some related works. For example, Lukasiewicz and Straccia[28]present probabilistic fuzzy description logic programs, which combine fuzzy description logics, fuzzy logic programs, and probabilistic uncertainty in a uniform framework for the Semantic Web, and define important concepts dealing with both probabilistic uncertainty and fuzzy vagueness, such as the expected truth value of a crisp sentence and the probability of a vague sentence. In this paper, we will further study intuitionistic fuzzy rough DLs. The main reasons are as follows.
(i) The intuitionistic fuzzy rough DLIFRALCpresented in [27] is an intuitionistic fuzzy rough extension of the DLALC[9]. It is well-known that inALC, there only exist concept negation, concept conjunction, concept disjunction, existential quantification, and universal quantification constructors. Therefore,IFRALCcan not deal with number restrictions, nominals, concrete domain, inverse roles, and role hierarchies, which are important ingredients of the DLsSHIF(D),SHOIN(D), andSROIQ(D). Moreover, these DLsSHIF(D),SHOIN(D), andSROIQ(D) are essentially the theoretical basis of the Web Ontology Language OWL, the state of the art language to specify ontologies[1,5-9]. In this paper, we will extend the intuitionistic fuzzy rough DLIFRALC[27]with the underlying DLSROIQ(D) which is the corresponding DL of the ontology description language OWL 2.
(ii) The intuitionistic fuzzy rough DLIFRALCpresented in[27] is based on the intuitionistic fuzzy rough set theory presented in[24]. It is well-known that combining intuitionistic fuzzy set theory and rough set theory may result in a new hybrid mathematical structure for the requirement of knowledge processing systems. Research on this topic has been investigated by a number of authors[23-25]. Various tentative definitions of intuitionistic fuzzy rough sets were explored to extend rough set theory to the intuitionistic fuzzy environment[23]. For example, Zhou and Wu[24]explored a general framework for the study of various relation-based intuitionistic fuzzy rough approximation operators when the intuitionistic fuzzy triangular norm=min. However, rough set models for approximations of intuitionistic fuzzy sets with respect to an arbitrary intuitionistic fuzzy approximation space on the basis of general intuitionistic fuzzy logical operators have not been studied. Since the intuitionistic fuzzy rough DLIFRALCpresented in[27] is based on the intuitionistic fuzzy rough set theory presented in[24], therefore, theIFRALCcan not express general intuitionistic fuzzy logical operators correspondingly. Zhou et al.[25]present a generalized (,)-intuitionistic fuzzy rough set theory by employing intuitionistic fuzzy logical operators in the intuitionistic fuzzy set theory proposed by Cornelis et al.[29]. This paper will present new intuitionistic fuzzy rough DLs based on the (,)-intuitionistic fuzzy rough set theory[25].
(iii) In fuzzy DLs (resp., fuzzy rough DLs, intuitionistic fuzzy rough DLs), there are crisp subsumption and fuzzy subsumption for fuzzy concepts (resp., fuzzy rough concepts, intuitionistic fuzzy rough concepts)[1,15-17]. The intuitionistic fuzzy rough DLIFRALC[27]considers the crisp subsumption. This paper will consider the fuzzy subsumption, i.e., subsumption relationship may hold to some degree which is taken from a complete lattice. The adopted approach is more general than the crisp subsumption based approach.
In this paper we extend the intuitionistic fuzzy rough DLIFRALC[27]from the above mentioned three aspects. More concretely, an intuitionistic fuzzy extension of the DLSROIQ(D) is defined[1,7-8], i.e., we present the intuitionistic fuzzy rough DLIFRSROIQ(D) based on the (,)-intuitionistic fuzzy rough set theory[25], and provide its syntax, semantics, and reasoning algorithms.
1 Preliminaries
1.1 Description Logic SROIQ(D)
DLs[6]are based on a common family of languages, called description languages, which provide a set of constructors to build concept (class) and role (property) descriptions. Such descriptions can be used in axioms and assertions of DL knowledge bases and can be reasoned about with respect to DL knowledge bases by DL systems[15].
SROIQ(D)[1,7]extendsSROIQ[1,8]with concrete domains[30], in other words,SROIQ(D) extendsALCstandard DL[9]with transitive roles (ALCplus transitive roles is calledS), complex role axioms (R), nominals (O), inverse roles (I), qualified number restrictions (Q) and concrete domains (D).
A concrete domain is a pairΔD,ΦD, whereΔDis a concrete interpretation domain andΦDis a set of concrete predicatesdwith a predefined aritynand an interpretationdD⊆(ΔD)n.
SROIQ(D) assumes three alphabets of symbols, for individuals, roles and concepts. Abstract individuals are denoteda,b. Concrete individuals are denotedv. The abstract roles (denoted byR) of the language can be built inductively according to the following syntax rule:R→RA|R-|U. Concrete roles are denotedTand cannot be complex. The concepts (denoted byCorD) of the language can be built inductively from atomic concepts (A), top concept, bottom concept ⊥, named individuals (oi), abstract roles (R), concrete roles (T), simple roles (S, which will be defined below) and concrete predicatesdas follows, wheren,mdenote natural numbers:
C,D→A||⊥|CD|CD|C|∀R.C|∃R.C|
∀R.d|∃R.d|{o1,…,om}|(≥nS.C)| (≤nS.
C)| (≥nT.d)| (≤nT.d)| ∃S.self.
Expression of the form (≥nS.C), (≤nS.C) are called qualified number restrictions, while expression of the form (≥nS), (≤nS) are called unqualified number restrictions. (=nS.C) is an abbreviation for (≥nS.C)(≤nS.C), and (=nS) is an abbreviation for (≥nS)(≤nS). The case for concrete number restrictions is similar.
AnSROIQ(D) knowledge base (KB) comprises two parts: the intensional knowledge, i.e., general knowledge about the application domain (a Terminological Box or TBoxTB, and a Role Box or RBoxRB), and the extensional knowledge, i.e., particular knowledge about some specific situation (an Assertional Box or ABoxABwith statements about individuals).
An ABox consists of a finite set of assertions about individuals:
•concept assertionsa:C;
•role assertions (a,b):R;
•negated role assertions (a,b):R;
•concrete role assertions (a,v):T;
•negated concrete role assertions (a,v):T;
•inequality assertionsa≠b;
•equality assertionsa≠b.
A TBox consists of a finite set of general concept inclusion (GCI) axiomsCD. We also say thatDis a superclass ofC, and thatCis a subclass ofD. A concept equivalenceC≡Dis a shorthand for the pair of axiomsCDandDC.
Letwbe a role chain (a finite string of roles not including the universal roleU). An RBox consists of a finite set of role axioms:
•role inclusion axioms (RIAs)wRorT1T2, in RIAs of the formR1R2we also say thatR2is a super-role ofR1, and thatR1is a sub-role ofR2;
•transitive role axiomstrans(R);
•disjoint role axiomsdis(S1,S2) ordis(T1,T2);
•reflexive role axiomsref(R);
•irreflexive role axiomsirr(S);
•symmetric role axiomssym(R);
•asymmetric role axiomsasy(S).
A role equivalenceR≡R′ is a shorthand for the pair of axiomsRR′ andR′R.
Simple roles are inductively defined as follows:
•RAis simple if does not occur on the right side of aRIA;
•R-is simple ifRis;
•ifRoccurs on the right side of aRIA,Ris simple if, for eachwR,w=Sfor a simple roleS.
Note that concrete roles are always simple and non-complex.
•w=RR, or
•w=R-, or
•w=S1…SnandSiRfor alli=1,…,n, or
•w=RS1…SnandSiRfor alli=1,…,n, or
•w=S1…SnRandSiRfor alli=1,…,n.
In order to guarantee the decidability of the logic, there are some restrictions in the use of roles:
•some concept constructors require simple roles: non-concrete qualified number restrictions and local reflexivity;
•some role axioms also require simple roles: disjoint, irreflexive and asymmetric role axioms;
•role axioms cannot contain the universal roleU;
An interpretationIwith respect to a concrete domainDis a pair (ΔI, •I) consisting of a non empty setΔI(the interpretation domain) disjoint withΔDand an interpretation function •Imapping:
•every abstract individualaonto an elementaIofΔI;
•every concrete individualvonto an elementvDofΔD;
•every atomic conceptAonto a setAI⊆ΔI;
•every abstract atomic roleRAonto a relation (RA)I⊆ΔI×ΔI;
•every concrete roleTonto a relationTI⊆ΔI×ΔD;
•everyn-ary concrete predicatedonto the interpretationdD⊆(ΔD)n.
The interpretation is extended to complex concepts and roles by the inductive definitions as follows, where #Xdenotes the cardinality of the setX:

•UI=ΔI×ΔI; ()I=ΔI; (⊥)I=;
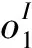
•(CD)I=CIDI; (CD)I=CIDI;









•Ia:C iffaICI;
•I(a,b):Riff (aI,bI)RI;
•I(a,b):Riff (aI,bI)RI;
•I(a,v):Tiff (aI,vD)TI;
•I(a,v):Tiff (aI,vD)TI;
•Ia=biffaI=bI;
•Ia≠biffaI≠bI;
•ICDiffCI⊆DI;
•IR1…Rn…RnI⊆RI;
•IT1T2iff (T1)I⊆(T2)I;
•Itrans(R) iff (x,y)RIand (y,z)RIimply (x,z)RI, ∀x,y,zΔI;
•Idis(S1,S2) iff (S1)I(S2)I=;
•Idis(T1,T2) iff (T1)I(T2)I=;
•Iref(R) iff (x,x)RI, ∀xΔI;
•Iirr(S) iff (x,x)SI, ∀xΔI;
•Isym(R) iff (x,y)RIimply (y,x)RI, ∀x,yΔI;
•Iasy(S) iff (x,y)SIimply (y,x)SI, ∀x,yΔI.
The interpretationI=(ΔI, •I) satisfies the axiom (or assertion)ω, orIis a model ofω, iffIω. We say thatIsatisfies a knowledge baseKB=(AB,TB,RB), orIis a model ofKB, denotedIKB, iffIωfor each axiom (or assertion) inAB,TB,RB. We say thatKBis satisfiable (resp., unsatisfiable) iffKBhas a (resp., no) model. An axiom (or assertion)ωis a logical consequence ofKB, denotedKBω, iff each model ofKBsatisfiesω.
A DL not only stores axioms and assertions, but also offers some reasoning services. Some important reasoning problems inSROIQ(D) are summarized as follows:
KBsatisfiability: given a knowledge baseKB, decide whetherKBis satisfiable;
concept satisfiability: given a knowledge baseKBand a conceptC, decide whetherKB/C⊥;
subsumption: given a knowledge baseKBand conceptsCandD, decide whetherKBCD;
instance: given a knowledge baseKB, an individuala, andaconceptC, decide whetherKBC(a); given a knowledge baseKB, individualsa,b(resp., an individualaand a valuev), and a roleR(resp.,), decide whetherKBR(a,b) (resp.,KBT(a,v)).
We can obtain the reasoning algorithm of concept satisfiability ofSROIQ(D) by integrating the reasoning algorithms of concept satisfiability ofSROIQ[8]andSHOQ(D)[30], that is to say, we need to extend theSROIQ-tableau algorithm[8]with datatype-rules[30-31].
1.2(,)-IntuitionisticFuzzyRoughSets
We first review a special lattice on [0, 1]×[0, 1] (where [0, 1] is the unit interval) and its logical operations originated by Cornelis et al.[29].
DenoteL*={(x1,x2)([0, 1]×[0, 1]|x1+x2≤1}. We define a relation ≤L*onL*as follows:

x1≤y1andx2≥y2.
Then the relation ≤L*is a partial ordering onL*and the pair (L*, ≤L*) is a complete lattice with the smallest element 0L*=(0, 1) and the greatest element 1L*=(1, 0)[25,29]. The meet operatorand the join operatoron (L*, ≤L*) which are linked to the ordering ≤L*are, respectively, defined as follows: ∀(x1,x2), (y1,y2)L*,
(x1,x2)(y1,y2)=(min(x1,y1), max(x2,y2)),
(x1,x2)(y1,y2)=(max(x1,y1), min(x2,y2)).

(y1,y2)≥L*(x1,x2)⟺(x1,x2)≤L*(y1,y2),
andx=y⟺x≤L*yandx≥L*y.
An intuitionistic fuzzy negator onL*is a decreasing mapping:L*→L*satisfying(0L*)=1L*and(1L*)=0L*. If((x))=xfor allxL*, thenis called an involutive intuitionistic fuzzy negator. The mappingS, defined asS(x1,x2)=(x2,x1), ∀(x1,x2)L*, is called the standard intuitionistic fuzzy negator.
Since ≤L*is a partial ordering, the order-theoretic definitions of conjunction and disjunction onL*called intuitionistic fuzzy triangular norm (intuitionistic fuzzy t-norm for short) and intuitionistic fuzzy triangular conorm (intuitionistic fuzzy t-conorm for short) are introduced as follows:
An intuitionistic fuzzy t-norm onL*is an increasing, commutative, associative mapping:L*×L*→L*satisfying(1L*,x)=xfor allxL*. An intuitionistic fuzzy t-conorm onL*is an increasing, commutative, associative mappingS:L*×L*→L*satisfyingS(0L*,x)=xfor allxL*.
An intuitionistic fuzzy t-normand an intuitionistic fuzzy t-conormSonL*are said to dual with respect to an intuitionistic fuzzy negatorif
((x),(y))=((x,y)), ∀x,yL*;
((x),(y))=((x,y)), ∀x,yL*.
(0L*, 0L*)=1L*,(1L*, 0L*)=0L*,
(0L*, 1L*)=1L*,(1L*, 1L*)=1L*.
Now we recall some basic notions of intuitionistic fuzzy sets presented by Atanassov[33]. LetUbe a nonempty set called the universe of discourse. The classes of all subsets (resp., fuzzy sets) ofUwill be denoted by(U) (resp.,(U)).
Let a setUbe fixed. An intuitionistic fuzzy setAinUis an object having the form
A={x,μA(x),γA(x)|xU},


We introduce some basic operations onI(U) as follows[25,33]: ∀A,BI(U),

•A⊇BiffB⊆A;
•A=BiffA⊆BandB⊆A;
•AB={x,min(μA(x),μB(x)),max(γA(x),γB(x))|xU};
•AB={x,max(μA(x),μB(x)),min(γA(x),γB(x))|xU}.
We know that an intuitionistic fuzzy relationR[25,35-36]onUis an intuitionistic fuzzy subsetU×U, namely,Ris given by
R={(x,y),μR(x,y),γR(x,y)|(x,y)U×U},







In general the round composition of intuitionistic fuzzy relationsR1,R2, …,Rn-1,RninI(U×U) is the intuitionistic fuzzy relationsR1R2…Rn-1RninI(U×U) defined by
(R1R2…Rn-1Rn)(x,y)=
Rn-1(yn-2,yn-1),Rn(yn-1,y)).
In what follows, we introduce the basic notions of (,)-intuitionistic fuzzy rough sets[25].
LetUbe a non-empty universe of discourse andRbe an intuitionistic fuzzy relation onU. The pair (U,R) is called an intuitionistic fuzzy approximation space.
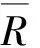
Let (U,R) be an intuitionistic fuzzy approximation space,andbe a continuous intuitionistic fuzzy t-norm and an intuitionistic fuzzy implicator onL*, respectively. Then the-upper intuitionistic fuzzy rough approximation operatorand the-lower intuitionistic fuzzy rough approximation operatorhave the following properties: ∀A,B,AiI(U) (∀iJ,Jis an index set),
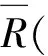
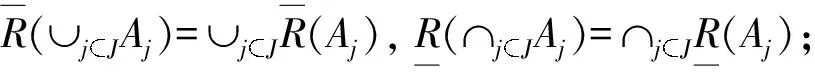
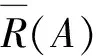
2 Intuitionistic Fuzzy Description Logic IFSROIQ(D)
The main goal of this paper is to provide intuitionistic fuzzy rough DLIFRSROIQ(D), which is the extension of intuitionistic fuzzy DLIFSROIQ(D).
IFSROIQ(D) is the fuzzy extension ofSROIQ(D) presented in Section 1.1 based on intuitionistic fuzzy set theory[25,33,35]. Obviously,IFSROIQ(D) is an extension of the intuitionistic fuzzy DLIFALC[27].
Definition1[7,17]A fuzzy concrete domainDis a pairΔD,ΦD, whereΔDis a concrete interpretation domain andΦDis a set of fuzzy concrete predicatesdwith an aritynand an interpretationdD: (ΔD)n→[0, 1], which is ann-ary fuzzy relation overΔD. In the following for simplicity we assume arity 1.

C,D→A||⊥|CD|CD|C|∀R.C|∃R.C|
∀T.d| ∃T.d| {α1/o1,…,αm/om}| (≥mS.
C)| (≤nS.C)| (≥mT.d)| (≤nT.d)|
∃S.self|mod(C)| [C≥L*α]| [C≤L*β].
The abstract roles (denoted byR) of the language can be built inductively according to the following syntax rule:R→RA|R-|U|mod(R)| [R≥L*α], whereUis a universal role.

In the rest of this paper we will assumeL*{≥L*, >L*, ≤L*, Definition3An intuitionistic fuzzy knowledge baseIFKBcomprises an intuitionistic fuzzy ABoxIFAB, an intuitionistic fuzzy TBoxIFTBand an intuitionistic fuzzy RBoxIFRB, i.e.,IFKB=IFAB,IFTB,IFRB. An intuitionistic fuzzy ABoxIFABconsists of a finite set of intuitionistic fuzzy assertions of one of the following types: •an intuitionistic fuzzy concept assertiona:C≥L*α,a:C>L*α,a:C≤L*αora:C •an intuitionistic fuzzy role assertionψ≥L*α,ψ>L*α,ψ≤L*αorψ An intuitionistic fuzzy TBoxIFTBconsists of a finite set of intuitionistic fuzzy GCIs (IFGCIsfor short) of the form (CDL*α, whereL*stands for ≥L*or >L*. An intuitionistic fuzzy RBoxIFRBconsists of a finite set of intuitionistic fuzzy role axioms of the following types: •intuitionistic fuzzyIFRIAswRL*α, wherew=R1R2…Rmis a role chain,T1T2L*α; •transitive role axiomstrans(R); •disjoint role axiomsdis(S1,S2),dis(T1,T2); •reflexive role axiomsref(R); •irreflexive role axiomsirr(S); •symmetric role axiomssym(R); •asymmetric role axiomsasy(S). Definition4Simple roles are defined as follows: •RAis simple if it does not occur on the right side of anIFRIA; •R-is simple ifRis simple; •ifRoccurs on the right side of anIFRIA,Ris simple if, for each (wRL*α,w=Sfor a simple roleS. As inFSROIQ(D), there are also some restrictions in the use of roles, in order to guarantee the decidability ofIFSROIQ(D). These restrictions are the same as that ofFSROIQ(D) (see [1] and [7] for more details). Obviously, the syntax ofIFSROIQ(D) is the extension of that ofFSROIQ(D)[1,7], i.e., theIFSROIQ(D) allows to express that a sentence is true to some degree, which is not taken from the unit interval[0, 1], but from the complete latticeL*. The semantics ofIFSROIQ(D) is also the extension of the semantics of fuzzy DLFSROIQ(D)[1,7]. Definition5An intuitionistic fuzzy interpretationIwith respect to a fuzzy concrete domainDis a tuple (ΔI, •I) consisting of a non empty setΔI(the interpretation domain) disjoint withΔDand an interpretation function •Imapping: •every abstract individualaonto an elementaIofΔI; •every concrete individualvonto an elementvDofΔD; •every conceptConto a functionCI:ΔI→L*; •every abstract roleRonto a functionRI:ΔI×ΔI→L*; •every concrete roleTonto a functionTI:ΔI×ΔD→L*; •everyn-ary concrete fuzzy predicatedonto the fuzzy relationdD: (ΔD)n→L*; •every modifiermodonto a functionfmod:L*→L*. Given arbitrary intuitionistic fuzzy t-norm, intuitionistic fuzzy t-conorm, intuitionistic fuzzy negatorand intuitionistic fuzzy implicator, the intuitionistic fuzzy interpretationIis extended to complex concepts and roles as follows, ∀xΔI: •(⊥)I(x)=0L*; •(CD)I(x)=(CI(x),DI(x)); •(CD)I(x)=(CI(x),DI(x)); •(∀R.C)I(x)=y ΔI{(RI(x,y),CI(y))}; •(∃R.C)I(x)=y ΔI{(RI(x,y),CI(y))}; •(∀T.d)I(x)=v ΔD{(TI(x,v),dD(v))}; •(∃T.d)I(x)=v ΔD{(TI(x,v),dD(v))}; •(≥mS.C)I(x)=y1,…,ymΔI[({(SI(x,yi),CI(yi))},j •(≤nS.C)I(x)=y1,…,yn+1ΔI[({(SI(x,yi),CI(yi))},j •(≥mT.d)I(x)=v1,…,vmΔD[({(TI(x,vi),dD(vi))},j •(≤nT.d)I(x)=v1,…,vn+1ΔD[({(SI(x,vi),dD(vi))},j •(∃S.self)I(x)=SI(x,x); •(mod(C))I(x)=fmod(CI(x)); •([C≥L*α])I(x)=1L*ifCI(x)(L*α, 0L*otherwise; •([C(L*β])I(x)=1L*ifCI(x)(L*β, 0L*otherwise; •(R-)I(x,y)=RI(y,x); •(U)I(x,y)=1L*; •(mod(R))I(x,y)=fmod(RI(x,y)); •([R≥L*α])I(x,y)=1L*ifRI(x,y)≥L*α, 0L*otherwise. As inFSROIQ(D), we do not impose unique name assumption, i.e., two nominals might refer to the same individual. The intuitionistic fuzzy interpretation function is extended to intuitionistic fuzzy axioms as follows: •(a:C)I=CI(aI); •((a,b):R)I=RI(aI,bI); •((a,b):R)I=(RI(aI,bI)); •((a,v):T)I=TI(aI,vD); •((a,v):T)I=(TI(aI,vD)); •(CD)I=xΔI{(CI(x),DI(x))}; •(R1…RmR)I=x1,…,xm+1ΔI{(((x1,x2), …,(xm,xm+1)),RI(x1,xm+1))}; •(T1T2)I=xΔI,vΔD{((x,v),(x,v))}. The satisfaction of an intuitionistic fuzzy axiom (or assertion)ωin an intuitionistic fuzzy interpretationI, denotedIω, is defined as follows: •Ia:CL*αiff (a:C)IL*α; •I(a,b):RL*αiff ((a,b):R)IL*α; •I((a,b):RL*αiff ((a,b):R)IL*α; •I(a,v):TL*αiff ((a,v):T)IL*α; •I((a,v):TL*αiff ((a,v):T)IL*α; •Ia≠biffaI≠bI; •Ia=biffaI=bI; •ICDL*αiff (CD)IL*α; •I(R1…RmRL*αiff (R1…RmR)IL*α; •IT1T2L*αiff (T1T2)IL*α; •Itrans(R) iff ∀x,yΔI,RI(x,y)≥L*zΔI{(RI(x,z),RI(z,y))}; •Idis(S1,S2) iff ∀x,yΔI,(x,y)=0L*or(x,y)=0L*; •Idis(T1,T2) iff ∀xΔI,yΔD,(x,y)=0L*or(x,y)=0L*; •Iref(R) iff ∀xΔI,RI(x,x)=1L*; •Iirr(S) iff ∀xΔI,SI(x,x)=0L*; •Isym(R) iff ∀x,yΔI,RI(x,y)=RI(y,x); •Iasy(S) iff ∀x,yΔI, ifSI(x,y)>L*0L*thenSI(y,x)=0L*. An intuitionistic fuzzy interpretationIsatisfies an intuitionistic fuzzy RBoxIFRB(writtenIIFRB) (resp., intuitionistic fuzzy TBoxIFTB(writtenIIFTB), intuitionistic fuzzy ABoxIFAB(writtenIIFAB)) iffIωfor all elementsωIFRB(resp.,ωIFTB,ωIFAB); in this case, we say thatIis a model ofIFRB(resp.,IFTB,IFAB). An intuitionistic fuzzy interpretationIsatisfies an intuitionistic fuzzy knowledge baseIFKB=IFAB,IFTB,IFRB, orIis a model ofIFKB, denotedIIFKB, iffIis a model ofIFRBIFTBIFAB, i.e.,IIFRB,IIFTB, andIIFAB. We sayIFKBis satisfiable (unsatisfiable) iff there exists (does not exist) an intuitionistic fuzzy interpretationIwhich satisfies all elements inIFKB. An intuitionistic fuzzy axiom (or assertion)ωis a logical consequence of an intuitionistic fuzzy knowledge baseIFKB, denotedIFKBω, iff every model ofIFKBsatisfiesω. LetCandDbe two concepts. We say thatCis subsumed byDto degreeαwith respect toIFKB(writtenFRKBCD≥L*α) if for every modelIofIFKBit holds thatICD≥L*α. An intuitionistic fuzzy ABoxIFABis consistent with respect toIFRBandIFTBif there exists a modelIofIFRBandIFTBsuch thatIIFAB. Similarly with the fuzzy DLFSHOIN(D)[11]andFSROIQ(D)[1,7], in addition to the standard reasoning problems defined above, two other important reasoning problems ofIFSROIQ(D) are the best truth certainty bound (BTCB) problem and the best satisfiability bound (BSB) problem, which we describe in the following. Given an intuitionistic fuzzy knowledge baseIFKBand a classical axiom (or assertion)ρ, whereρis neither a transitive role axiom, disjoint role axiom, reflexive role axiom, irreflexive role axiom, symmetric role axiom, or asymmetric role axiom nor an equality or inequality axiom, it is of interest to computeρ’s best lower and upper certainty value bounds (best certainty value bound). The greatest lower bound ofρwith respect toIFKB, denoted byglb(IFKB,ρ), is defined byglb(IFKB,ρ)={α|IFKBρ≥L*α}, whereφ=0L*. Similarly, the least upper bound ofρwith respect toIFKB, denoted bylub(IFKB,ρ), is defined bylub(IFKB,ρ)={α|IFKBρ≤L*α}, whereφ=1L*. The best satisfiability bound of a conceptCwith respect toIFKB, denoted byglb(IFKB,C), is defined byglb(IFKB,C)=IxΔI{CI(x)|IIFKB}. Intuitively, among all modelsIofIFKB, we determine the maximal degree of certainty that the conceptCmay have over all individualsxΔI. In the current section, we will provide the intuitionistic fuzzy roughIFRSROIQ(D). This includes the syntax, semantics, and reasoning ofIFRSROIQ(D). In fact,IFRSROIQ(D) is also a rough extension of the intuitionistic fuzzy DLIFSROIQ(D) presented in Section 2. 3.1 Syntax and Semantics C,D→A||⊥|CD|CD|C|∀R.C|∃R.C| ∀T.d|∃T.d|{α1/o1,…,αm/om}|(≥mS.C)| (≤nS.C)|(≥mT.d)|(≤nT.d)|∃S.self| Regarding the definitions of the abstract roles, concrete roles, intuitionistic fuzzy rough knowledge base, and simple roles ofIFRSROIQ(D), it is similar to that ofIFSROIQ(D). For example, an intuitionistic fuzzy rough TBoxIFRTBconsists of a finite set of intuitionistic fuzzy rough GCIs (IFRGCIsfor short) of the formCD≥L*αorCD>L*α, whereCandDare concepts ofIFRSROIQ(D). Comparing with theIFGCIofIFSROIQ(D), theIFRGCIofIFRSROIQ(D) can have intuitionistic fuzzy lower approximation concepts and intuitionistic fuzzy upper approximation concepts. Regarding the semantics of intuitionistic fuzzy rough knowledge base and the reasoning problems ofIFRSROIQ(D), they are similar to that ofIFSROIQ(D). For instance, an intuitionistic fuzzy rough interpretationIsatisfiesCDL*α, denotedICDL*α, iff (CD)IL*α. Comparing with classical DLs[6], fuzzy DLs[1,14-18], and intuitionistic fuzzy DLs (see Section 2 and [27]), the most distinguished characteristic of intuitionistic fuzzy rough DLIFRSROIQ(D) is that TBox and ABox have the intuitionistic fuzzy lower approximation concepts and intuitionistic fuzzy upper approximation concepts inIFRSROIQ(D). Theorem1For any conceptsC,D, and intuitionistic fuzzy-equivalence relationinIFRSROIQ(D), their intuitionistic fuzzy lower and intuitionistic fuzzy upper approximation concepts satisfy the following properties: (7)CD⟹ (8)CD⟹). Proof to be omitted. 3.2 Reasoning In this section, we will prove that the reasoning problems inIFRSROIQ(D) may be reduced to the corresponding reasoning in the intuitionistic fuzzy DLIFSROIQ(D). Given an arbitrary conceptCinIFRSROIQ(D), we define a translation function •t:IFRSROIQ(D)→IFSROIQ(D) fromIFRSROIQ(D) toIFSROIQ(D) that fulfills the following conditions: •At=A; •⊥t=⊥; •{α1/o1,…,αm/om}t={α1/o1,…,αm/om}; •(CD)t=CtDt; •(CD)t=CtDt; •(∃R.C)t=∃R.Ct; •(∀R.C)t=∀R.Ct; •(∃S.Self)t=∃S.Self; •(≥mS.C)t=≥mS.Ct; •(≤nS.C)t=≤nS.Ct; •(∃T.d)t=∃T.d; •(∀T.d)t=∀T.d; •(≥mT.d)t=≥mT.d; •(≤nT.d)t=≤nT.d; •(mod(C))t=mod(Ct); •([C≥L*α])t=[Ct≥L*α]; •([C≤L*β])t=[Ct≤L*β]; Given an arbitraryIFRGCICDL*αinIFRSROIQ(D), we can translate theIFRGCICDL*αinIFRSROIQ(D) into anIFGCICtDtL*αinIFSROIQ(D) using the above translation function •t. Given an arbitrary intuitionistic fuzzy rough TBoxIFRTB={C1D1L*α1, …,CkDkL*αk} inIFRSROIQ(D), we can translate theIFRTB={C1D1L*α1, …,CkDkL*αk} into an intuitionistic fuzzy TBoxIFRTBt={(C1)t(D1)tL*α1, …,(Ck)t(Dk)tL*αk} inIFSROIQ(D) using the above translation function •t. Given an arbitrary intuitionistic fuzzy rough ABoxIFRAB={a1:C1L*α1, …,ap:CpL*αp,ψ1L*β1, …,ψqL*βq,a11=b11, …,a1s=b1s,a21≠b21, …,a2t≠b2t} inIFRSROIQ(D), whereψiis of the form (a,b):R, (a,b):R, (a,v):T, or (a,v):T, we can translate the intuitionistic fuzzy rough ABoxIFRABinto an intuitionistic fuzzy ABoxIFRABt={a1:L*α1, …,ap:L*αp,ψ1L*β1, …,ψqL*βq,a11=b11, …,a1s=b1s,a21≠b21, …,a2t≠b2t} inIFSROIQ(D) using the above translation function •t. Given an arbitrary intuitionistic fuzzy (rough) RBoxIFRRB={ω1, …,ωl} inIFRSROIQ(D), whereωi(1≤i≤l) is anIFRRIAof the formwiRiL*αiorT1iT2iL*βi, or a role assertion of the formtrans(R),dis(S1,S2),dis(T1,T2),ref(R),irr(S),sym(R) orasy(S), we can translate the intuitionistic fuzzy (rough) RBoxIFRRBinto an intuitionistic fuzzy RBoxIFRRBt={ref(),sym(),trans(), …,ref(),sym(),trans(),ω1, …,ωl} inIFSROIQ(D) using the above translation function •t. Given an arbitrary intuitionistic fuzzy rough knowledge baseIFRKB=IFRAB,IFRTB,IFRRBinIFRSROIQ(D), we can theIFRKBinto an intuitionistic fuzzy knowledge baseIFRKBt=IFRABt,IFRTBt,IFRRBtinIFSROIQ(D) using the above translation function •t. In the following, we prove the correctness of the translation function •t, i.e., we prove that the satisfiability, subsumption, logical consequence, ABox consistency, BTCB, and BSB reasoning inIFRSROIQ(D) may be reduced to the corresponding reasoning inIFSROIQ(D). Theorem2Given an intuitionistic fuzzy rough knowledge baseIFRKB=IFRAB,IFRTB,IFRRBinIFRSROIQ(D),IFRKBt=IFRABt,IFRTBt,IFRRBtis the intuitionistic fuzzy knowledge base inIFSROIQ(D) obtained from the translation function •t.IFRKBis satisfiable, iffIFRKBtis satisfiable. Theorem3Given a conceptC, an intuitionistic fuzzy rough knowledge baseIFRKB=IFRAB,IFRTB,IFRRBinIFRSROIQ(D),CtandIFRKBt=IFRABt,IFRTBt,IFRRBtare the concept and the intuitionistic fuzzy knowledge base inIFSROIQ(D) obtained from the translation function •t, respectively.Cisα-satisfiable with respect toIFRKB, iffCtisα-satisfiable with respect toIFRKBt. Theorem4Given two conceptsC,D, and an intuitionistic fuzzy rough knowledgeIFRKBinIFRSROIQ(D),CtandDt, andIFRKBtare the concepts, and intuitionistic fuzzy knowledge base inIFSROIQ(D) obtained from the translation function •t, respectively.Cis subsumed byDto degreeαwith respect toIFRKBiffCtis subsumed byDtto degreeαwith respect toIFRKBt. Formally,IFRKBCDL*αiffIFRKBtCtDtL*α. Theorem5Given an intuitionistic fuzzy rough axiom (or assertion)ω, and an intuitionistic fuzzy rough knowledgeIFRKBinIFRSROIQ(D),ωtandIFRKBtare the intuitionistic fuzzy axiom (or assertion) and intuitionistic fuzzy knowledge base inIFSROIQ(D) obtained from the translation function •t, respectively.ωis a logical consequence ofIFRKB, iffωtis a logical consequence ofIFRKBt. Formally,IFRKBωiffIFRKBtωt. Theorem6Given an intuitionistic fuzzy rough ABoxIFRAB, an intuitionistic fuzzy rough TBoxIFRTB, and an intuitionistic fuzzy rough RBoxIFRRBinIFRSROIQ(D),IFRABt,IFRTBt, andIFRRBtare the intuitionistic fuzzy ABox, intuitionistic fuzzy TBox, and intuitionistic fuzzy RBox inIFSROIQ(D) obtained from the translation function •t, respectively.IFRABis consistent with respect toIFRRBandIFRTB, iffIFRABtis consistent with respect toIFRRBtandIFRTBt. Theorem7Given an intuitionistic fuzzy rough knowledgeIFRKB=IFRAB,IFRTB,IFRRB, an axiom (or assertion)ρ, whereρis neither a transitive role axiom, disjoint role axiom, reflexive role axiom, irreflexive role axiom, symmetric role axiom, or asymmetric role axiom nor an equality or inequality axiom, and a conceptCinIFRSROIQ(D),IFRKBt=IFRABt,IFRTBt,IFRRBt,ρt, andCtare the intuitionistic fuzzy knowledge base, axiom (or assertion), and concept inIFSROIQ(D) obtained from the translation function •t, respectively. Then (1)glb(IFRKB,ρ)=glb(IFRKBt,ρt); (2)lub(IFRKB,ρ)=lub(IFRKBt,ρt); (3)glb(IFRKB,C)=glb(IFRKBt,Ct). Handling uncertainty and vagueness has started to play an important role in ontology languages for the Semantic Web. An integration between the theories of expressive intuitionistic fuzzy DLs and expressive rough DLs has been provided. More concretely, towards sophisticated formalisms for reasoning under fuzzy uncertainty and rough uncertainty in the Semantic Web, we have presented a kind of very expressive intuitionistic fuzzy rough DLIFRSROIQ(D), which is the intuitionistic fuzzy rough extension of the expressive DLSROIQ(D) behind OWL 2 based on (,)-intuitionistic fuzzy rough set theory. We have proved that the main reasoning tasks in theIFRSROIQ(D) may be reduced to the corresponding reasoning in the fuzzy DL over complete latticesL*-SROIQ(D). As far as future directions are concerned, these will include the extension of the DLSROIQ(D) based on probabilistic rough set theory and interval-valued (fuzzy) rough set theory, in order to provide reasoning support for the probabilistic rough DLs and interval-valued (fuzzy) rough DLs, respectively. [1] BOBILLO F,DELGADO M,GOMEZ-ROMERO J,et al.Fuzzy description logics under Gödel semantics[J]. Int J Approx Reason, 2009,50(3): 494-514. [2] BERNERS-LEE T, HENDLER J, LASSILA O. The semantic Web[J]. Scientific American,2001,284(5):34-43. [3] PATEL-SCHNEIDER P F,HORROCKS I.A comparison of two modelling paradigms in the Semantic Web[J]. J Web Semant,2007,5(4):240-250. [4] GRUBER T R. A translation approach to portable ontology specifications[J].Knowledge Acquisition,1993, 5(2):199-220. [5] HORROCKS I,PATEL-SCHNEIDER P F,HARMELEN F V. From SHIQ and RDF to OWL: The making of a Web ontology language[J]. J Web Semant,2003,1(1):7-26. [6] BAADER F,CALVANESE D,MCGUINNESS D,et al.The description logic handbook: Theory, implementation and applications[M]. 2nd Ed. Cambridge:Cambridge University Press, 2007. [7] BOBILLO F. Managing vagueness in ontologies[D]. Spain:University of Granada, 2008. [8] HORROCKS I,KUTZ O,SATTLER U.The even more irresistible SROIQ[C]∥DOHERTY P, MYLOPOULOS J, WELTY C.Proceedings of the 10th international conference of knowledge representation and reasoning.Palo Alto, California, USA:AAAI Press, 2006:57-67. [9] HORROCKS I, PATEL-SCHNEIDER P.Reducing OWL entailment to description logic satisfiability[J]. J Web Semant,2004,1(4):345-357. [10] SANCHEZ E.Fuzzy logic in the Semantic web: Covering a missing link[M]∥SANCHEZ E.Capturing intelligence: Fuzzy logic and the semantic web, Elsevier, 2006:ix-xiii. [11] LUKASIEWICZ T,STRACCIA U.Managing uncertainty and vagueness in description logics for the Semantic Web[J].J Web Semant,2008,6(4):291-308. [12] LUKASIEWICZ T.Expressive probabilistic description logics[J].Artif Intell,2008,172(6-7) : 852-883. [13] HOLLUNDER B.An alternative proof method for possibilistic logic and its application to terminological logics[J]. Int J Approx Reason,1995,12(2):85-109. [14] BOBILLO F,STRACCIA U. Fuzzy description logics with general t-norms and datatypes[J]. Fuzzy Set Syst,2009,160(23):3382-3402. [15] STOILOS G,STAMOU G,PAN J Z, et al.Reasoning with very expressive fuzzy description logics[J].J Artif Intell Res, 2007,30(8):273-320. [16] STRACCIA U.Reasoning within fuzzy description logics[J]. J Artif Intell Res, 2001, 14:137-166. [17] STRACCIA U.A fuzzy description logic for the Semantic Web[M]∥SANCHEZ E.Capturing intelligence: Fuzzy logic and the semantic web.Amsterdam, Netherlands:Elsevier Science Publishers, 2006:73-90. [18] STRACCIA U.Description logics over lattices[J].Int J Uncertain Fuzz,2006,14(1):1-16. [19] JIANG Y,WANG J,TANG S,et al.Reasoning with rough description logics: An approximate concepts approach[J]. Inform Sciences,2009,179(5):600-612. [20] SCHLOBACH S,KLEIN M,PEELEN L.Description logics with approximate definitions: Precise modeling of vague concepts[C]∥VELOSO M M.Proceedings of the 20th international joint conference on artificial intelligence, Palo Alto, California, USA:AAAI Press, 2007:557-562. [21] DUBOIS D, PRADE H. Rough fuzzy sets and fuzzy rough sets[J].Int J Gen Syst, 1990,17(2-3):191-209. [22] MI J,LEUNG Y,ZHAO H,et al.Generalized fuzzy rough sets determined by a triangular norm[J].Inform Sciences,2008,178(16):3203-3213. [23] CORNELIS C,COCK M D,KERRE E E.Intuitionistic fuzzy rough sets: At the crossroads of imperfect knowledge[J]. Expert System, 2003,20(5):260-270. [24] ZHOU L,WU W.On generalized intuitionistic fuzzy rough approximation operators[J].Inform Sciences, 2008,178(11):2448-2465. [25] ZHOU L,WU W,ZHANG W.On characterization of intuitionistic fuzzy rough sets based on intuitionistic fuzzy implicators[J]. Inform Sciences,2009,179(7):883-898. [26] JIANG Y,WANG J,DENG P, et al.Reasoning within expressive fuzzy rough description logics[J].Fuzzy Set Syst,2009,160(23):3403-3424. [27] JIANG Y,TANG Y,WANG J,et al.Reasoning within intuitionistic fuzzy rough description logics[J].Inform Sciences,2009,179(14):2362-2378. [28] LUKASIEWICZ T,STRACCIA U.Description logic programs under probabilistic uncertainty and fuzzy vagueness[J]. Int J Approx Reason,2009,50(6):837-853. [29] CORNELIS C,DESCHRIJVER G, KERRE E E.Implication in intuitionistic fuzzy and interval-valued fuzzy set theory: Construction, classification, application[J]. Int J Approx Reason,2004: 35(1):55-95. [30] LUTZ C,ARECES C,HORROCKS I,et al.Keys, nominals, and concrete domains[J].J Artif Intell Res,2005,23:667-726. [31] MOTIK B,HORROCKS I.OWL datatypes: Design and implementation[C]∥Proceedings of the 7th international Semantic Web conference, Lecture notes in computer science. New York:Springer-Verlag, 2008,5318:307-322. [32] PAWLAK Z. Rough sets: Theoretical aspects of reasoning about data[M].Dordrecht,Netherlands:Kluwer Academic Publishers, 1991. [33] ATANASSOV K. Intuitionistic fuzzy sets[M]. Heidelberg/New York :Physica-Verlag, 1999. [34] DESCHRIJVER G,KERRE E F. On the relationship between some extensions of fuzzy set theory[J].Fuzzy Set Syst,2003,133(2):227-235. [35] DESCHRIJVER G,KERRE E E.On the composition of intuitionistic fuzzy relations[J].Fuzzy Set Syst, 2003,136(3):333-361. [36] BUSTINCE H,BURILLO P. Structures on intuitionistic fuzzy relations[J].Fuzzy Set Syst,1996,78(3):293-303. 2013-09-24 国家自然科学基金项目(61272066);教育部新世纪优秀人才支持计划项目(NCET-12-0644);广东省自然科学基金项目(S2012030006242,10151063101000031) 1000-5463(2013)06-0042-14 TP301 A 10.6054/j.jscnun.2013.09.006 面向语义Web的直觉模糊粗描述逻辑 蒋运承* (华南师范大学计算机学院,广东广州 510631) 分析了面向语义Web的直觉模糊粗描述逻辑的研究现状和存在的问题,基于(L,T)-直觉模糊粗集理论将直觉模糊描述逻辑和粗描述逻辑进行了集成,即提出了一种新的直觉模糊粗描述逻辑.针对与本体语言OWL 2等价的描述逻辑SROIQ(D),对SROIQ(D)进行了扩充,提出了直觉模糊粗描述逻辑IFRSROIQ(D),给出了IFRSROIQ(D)的语法、语义和性质,证明了IFRSROIQ(D)的推理问题(包括知识库可满足性、概念可满足性、概念包含、逻辑推导、ABox一致性推理等)可以归约到基于完备格的描述逻辑L*-SROIQ(D)上对应的推理. 描述逻辑; 模糊描述逻辑; 粗描述逻辑;(L,T)-直觉模糊粗集; 语义Web *通讯作者:蒋运承,教授,Email: ycjiang@scnu.edu.cn, yunchengjiang@gmail.com. 【中文责编:庄晓琼 英文责编:肖菁】

3 Intuitionistic Fuzzy Rough Description Logic IFRSROIQ(D)
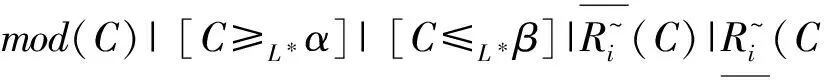
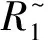
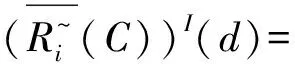
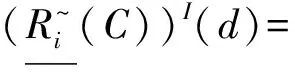
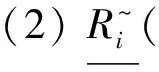
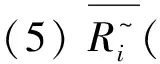

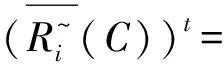

4 Conclusion
猜你喜欢
杂志排行
华南师范大学学报(自然科学版)的其它文章
- 复域差分和差分方程的研究
- Time Periodic Solution of the Relativistic Boltzmann Equation
- Method of Constructing Upper-Lower Solutions for Wave Profile Systems with Quasi-Monotonicity
- 地铁站点周边的商业集聚及其影响因素
- 不同时间电刺激对C2C12细胞糖代谢的影响研究
- Biogeographic and Phylogenetic Relationships of Some Scincella (Squamata: Scincidae) from China and North America Inferred from 12S rRNA Gene Sequences of Mitochondrial DNA
