全空间RN中反应扩散方程的非平面行波解
2013-10-27尹景学
黄 锐, 尹景学
(华南师范大学数学科学学院, 广东广州 510631)
全空间RN中反应扩散方程的非平面行波解
黄 锐, 尹景学*
(华南师范大学数学科学学院, 广东广州 510631)
介绍全空间RN中反应扩散方程非平面行波解的主要研究结果. 通过分析本生灯模型作为非平面行波解的一个例子,给出问题的偏微分方程模型, 以及具有鲜明实际背景的点火温度型和双稳态型这2 种重要的非线性源. 然后介绍具有这2 种非线性源的方程非平面行波解的一些定性性质, 包括解的存在唯一性、 单调性、稳定性和水平集的性质等. 讨论了具有KPP型非线性源的方程无穷维非平面行波解流形的存在性,以及解的单调性、稳定性和最小波速的性质等.同时提出了该研究领域内尚未解决的问题.
反应-扩散方程; 非平面; 行波解
反应扩散方程是研究自然界中广泛存在的扩散现象的有力工具, 作为它的一类特殊解的行波解,特别是非平面行波解,具有鲜明的物理背景. 早在1906 年,LUTHER[1]第一次考虑把行波解作为反应扩散方程的解. 然而关于行波解的极其重要的开创性的工作则分别由FISHER[2]和 KOLMOGOROV等[3]在1937年独立完成. 此后, 关于反应扩散方程的行波解的研究便蓬勃发展起来.根据不同的背景, 反应扩散方程的非线性源有大量的不同表现形式. 在这些非线性源中,点火温度、双稳态以及KPP(Kolmogorov-Petrovsky-Piskunov) 等3种非线性源具有鲜明的实际背景.具有上述3 种非线性源的反应扩散方程的非平面行波解是近年来才被人们所认识并研究的一类具有特殊性质的解.和平面行波解相比较, 非平面行波解的性质变得更加复杂, 但同时也更加有意义, 这在一定程度上促进了数学理论的发展.本文将分别介绍近年来出现的含几种重要的非线性源的非平面行波解的一些结果.
1 非平面行波解的一个例
预混本生灯火焰是非平面行波解的一个典型例子. 一个本生灯火焰可以被分成两部分: 扩散火焰部分和预混火焰部分[4-11]. 而预混火焰本身又可以被分成两部分: 位于下部的由燃料和氧气组成的冷温区域和位于上部的由燃烧生成气体组成的高温区域. 简单起见, 假设在混合物中发生单一的化学反应:
燃料+氧→成物.
假定火焰在向上的方向上是稳定的且具有一致的速度c. 那么, 在这个模型中温度的水平集是锥状的, 且在远离对称轴的地方,水平集趋于平坦, 见图1.

图1 本生灯和预混火焰模型
由于火焰的形状相对于本生灯的大小是不变的, 因而可以在全空间

中来考虑模型的建立.在经典的热扩散理论下,温度场u满足下面的反应扩散方程

(1)
其中u的取值在全空间中可以被正则化为介于0,1之间. 事实上, 假定f在(-∞,0)上是正的,在(1,+∞)上是负的,若u是方程(1)的有界解, 那么由比较原理容易证明在RN上恒有0≤u≤1. 非线性反应项f(u)满足所谓的“点火温度”型条件,即f在区间[0,1]上满足Lipschitz连续性条件,在1点附近可微, 且


(2)
实数θ是点火温度. 低于点火温度时, 没有反应发生, 高于点火温度时才有反应发生. 为了数学讨论上的方便, 还假设在[0,1]以外f≡0.
数学上的主要困难在于用温度u的合理的数学条件来刻画火焰的锥状结构.把火舌的张角考虑进所加的条件中是一个自然的想法. 具体地说, 如果α表示火舌的张角, 那么可以在无穷远处加上如下的渐近锥条件
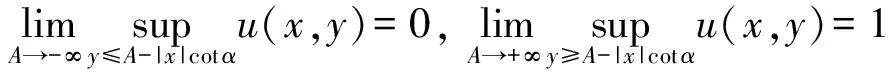
(3)
因此,在u接近于0的区域表示新鲜的混合物且在竖直的方向远远低于由α确定的锥状面.而在u接近于1的区域表示由已燃气体组成的区域,在竖直的方向上它远远高于由α确定的锥状面. 本生灯出口处气流的速度c是给定的,且c的大小决定了火舌张角α的大小.事实上也可以假设α的大小是给定的,而α的大小决定了速度的大小c,2种假设是等价的.不妨假设α是给定的,而c未知.当空间维数N≥3 时, 上面的渐近锥条件似乎有些过强, 在这种情况下可以给出一些较弱的条件, 此处不再叙述.
在其他模型中也能找到锥状行波解的例子. 比如在具双稳态型非线性源的Allen-Cahn方程中存在V状行波解.这种双稳态型的非线性源f满足在[0,1]上是Lipchitz连续的,在0,1两点是可微的. 且满足如下的条件

f(0)=f(θ)=f(1)=0,
f′(0)<0,f′(1)<0,f′(θ)>0.
(4)
关于这类非线性源的一个典型的例子是f(s)=s(1-s)(s-θ).
近年的研究发现, 燃烧模型中的锥状行波解和Allen-Cahn方程中的V状行波解有许多相似的性质.其实, 方程(1)的解也可以被看成是在静态的介质中以速度c向下传播的如下形式的行波解
v(t,x,y)=u(x,y+ct).
函数v满足如下的抛物型方程
vt=Δv+f(v).
(5)
在一维情形下方程(1)、条件(3)化为如下的常微分方程
u″-cu′+f(u)=0,u(-∞)=0,u(+∞)=0.
(6)

2 非平面行波解的性质
在这节中,介绍具非线性源(2)或(4)的方程(1)的锥状行波解的单调性、唯一性、稳定性和其他定性性质.总假设函数f在R上满足Lipschitz连续性条件且f(0)=f(1)=0. 一些结论对于更一般的在0,1两点附近满足单调不增条件的函数f仍然成立.
2.1 锥方向上的单调性和水平集的一些性质
下面介绍方程(1)的解u在锥方向上的单调性以及解的水平集的若干性质.
HAMEL等[20-21]证明了如下的结果:假定f在(0,θ1)上是负的,在(θ2,1)上是正的, 其中0<θ1≤θ2<1.若0≤u≤1是方程(1)满足下面条件的解

其中φ是从RN-1到R上的Lipschitz函数.那么,在RN上0 (7) 更进一步地,假定函数f属于C1([0, 1]),并且存在δ>0使得f在[0,δ]和[1-δ,1]上是单调非增的.若0≤u≤1是方程(1)满足条件(7)的解.那么,对每个(0,1),水平集{(x,y)RN-1×R,u(x,y)=}的图像{y=φ(x),xRN-1}是Lipschitz的,并且u满足 (8) 而且, 所有的水平集φ具有相同的Lipschitz模‖φ‖Lip=cotα,其中α(0,π/2],且‖φ‖Lip≤‖φ‖Lip. ∀,φ(x))>0. 2.2 速度的唯一性和水平集方向上的渐近性 HAMEL等[20-22]找到了行波的速度c和由行波的水平集所确定的一个角度以及一个一维问题的唯一的波速之间的联系. 事实上, 我们已知如果f在[0,δ]和[1-δ,1]上是单调不增的, 那么方程 u″-c0u′+f(u)=0, (9) u(-∞)=0≤u≤u(+∞)=1,u(0)=1/2 1)如果存在一个径向对称的Lipschitz 连续函数φ:RN-1→R满足条件(7),那么上小节中关于锥方向上的单调性和水平集的性质的结论成立. 并且问题(9)存在一组解(c(f),u),使得 c=c(f)/sinα. (10) 2)如果N=2且存在一个Lipschitz连续函数φ:R→R满足条件(7),那么第1条的结论成立. 如果f满足点火温度型的条件(2),那么问题(9)有唯一的一个解,且速度c(f)是正的. 因此, 对于第一节中的本生灯模型,可以知道非平面火焰的波速c=c(f)/sinα大于平面行波的波速c0=c(f). 而且随着波速c的变大,火舌张角α会变小.这具有明显的物理意义, 和物理实际非常吻合.值得注意的是式(10)早就被物理学家发现并在实际中所使用, 但是BONNET等[22]第一次给出它的数学证明.这条公式在实际的实验中, 经常被用来找平面行波的波速c0=c(f): 事实上, 若已知在本生灯的出口处燃烧气体在垂直方向的速度c,估计了角度α以后, 一维的速度c0=c(f)就由c(f)=csinα给出[4,7,9,11]. 事实上, 也可以从解沿着水平集的方向上的渐近性质得到式(10). 如果把介质看成是静态的, 那么火焰以速度c向下运动, 并以速度c(f)沿着垂直于它的水平集的方向上运动.因为水平集和竖直方向的夹角是渐近等于α的,所以速度c(f)就必然是波速c在垂直于水平集方向上的投影. 2.3 锥状行波解的整体弯曲度, 行波形状的唯一性 2.4 解的稳定性 下面介绍方程(1)满足渐近条件(7)的解u的整体稳定性.关于解的稳定性问题的另外一种表述为寻求下述Cauchy问题的解v(t,x,y)是否收敛到行波解u(x,y+ct)或者u(x,y+ct)的某个平移. (11) 其中v0(x,y)是给定的在某种程度上接近于方程(1)的解u的一个平移u(·+a,·+b). HAMEL等[35]证明了这样的稳定性结果:对于二维空间情形,假定f满足点火温度型条件(2)或f在0,1两点处都具有负的导数.那么,如果在无穷远处v0指数地趋近于行波解u,则在具速度c向下移动的坐标系下,v关于时间t一致地收敛到u.特别地,如果v0-u具有紧支集,那么上述关于v0的条件自然满足.事实上,可以在加权Banach空间中得到更加精确的收敛性结果.进一步还可以发现收敛性结果实际上和空间变量沿着方向(±sinα,cosα)趋于无穷时初值的取值密切相关,其中α是相对于向量(0,-1)的一个角度. 当f满足点火温度型条件(2)时上述结果在文献[35]中给出了证明.证明的想法是先对方程(1)做线性化,然后分析这个线性化以后的算子,并结合平面行波解的指数稳定性的相关结果.利用类似的方法可以证明当f在0,1两点处都具有负导数时,相应的结果依然成立[36]. 本节归纳具点火温度型和双稳态型非线性源的方程(1)的锥状行波解的存在性结果. 3.1 具点火温度型非线性源的情形 3.2 具双稳态型非线性源的情形 3.3 其他一些存在性结果 HAMEL等[37]对于二维空间情形下的具双稳态型非线性源的方程(1)得到了一些更加精确的结果.即,对于2维空间情形,解u满足锥条件(3),且水平集φ指数收敛到平行于{y=±cotα}的直线.这个存在性结果对于更一般的满足f′(0)<0,f′(1)<0且f>0 (0≤s<1)的非线性源f都成立[36].事实上,当空间维数N=2且角度α<π/2并接近于π/2时,可以用中心流形定理来证明方程(1)满足渐近锥条件(3)的解(c,u)的存在性[23,38]. φ,当∞. 当空间维数N≥3时,有 φ,当∞. f(0)=f(1)=0,f′(0)>0,f′(1)<0, (12) 满足上述条件的一个典型的例子是f(s)=s(1-s).具Fisher-KPP型源的反应扩散方程来源于人口动力学模型.众所周知,当空间维数N≥2时,方程vt=Δv+f(v)的平面行波解构成N+1维流形,即 vν,c,h(t,z)=φc(z·ν+ct+h), 对任何c≥c*,函数φc满足 函数φc是单调递增的且在平移的意义下是唯一的.对任何c≥c*,令c是由下式确定的正实数 ∀c>c*,φc(s)~e(s→-∞). 已经有许多工作研究方程vt=Δv+f(v)的Cauchy问题解的长时间行为问题和解长时间是否收敛到行波解的问题.特别是在一维空间情形, 在一类相当广泛的初值条件下有许多结果[24]. 我们知道,若方程的非线性源f在0,1附近的某个小区间上单调不增,那么满足方程(9)的波速c(f)如果存在,必唯一.但是对于满足条件(12)的非线性源方程的情况就截然不同.我们将要说明,由来自不同方向和具有不同波速的平面行波解经过混合可以构造出非平面行波解,且这些非平面行波解构成一个无穷维的流形.特别地,有无穷多的行波解满足方程(1)和渐近锥条件(3).我们也会介绍一些关于行波解的单调性和稳定性的结果. 4.1 无穷维非平面行波解流形的存在性 已知,抛物方程 vt=Δv+f(v) (13) Δy-cuy+f(u)=0. 反过来,方程(1)的任何一个解u都给出抛物方程(13)的一个行波解u(x,y+ct)=v(t,x,y). 在介绍无穷维非平面行波解流形的存在性之前,首先给出一些记号.假设空间维数N≥2,令 为RN中以0为心、c*为半径的开球.RN中所有单位向量构成的集合记为SN-1.定义集合 {S(ceN/2,c/2)B(0,c*)}, 其中S(ceN/2,c/2)是以ceN/2为心、c/2为半径的球面.令为定义在X上的所有非负非零Radon测度μ(0<μ(X)<+∞)的集合, 使得测度μ在球面SN-1×{c*}上的限制μ*可以写成有限个Dirac测度之和: TW={μ;∃c[c*,+∞),μ集中于S(ν,c)}. TWμuμ, 使得每个函数uμ都是方程(1)的介于区间(0,1)的解. 上述结果特别蕴含了这样一个事实:如果非线性项f满足条件(12),方程(1)在锥条件(3)下的解不具唯一性.事实上,如果f满足条件(12),N≥2,0<α<π/2,csinα>c*, 那么,方程(1)满足条件(3)的解构成一个无穷维流形.可见,Fisher-KPP方程比具点火温度型或双稳态型非线性源的方程具有更多的解. 4.2Fisher-KPP方程非平面行波解的定性性质 关于Fisher-KPP方程非平面行波解的单调性,HAMEL等[48]证明了:假定f满足条件(12),N≥2,若对某个c≥0,0 HUANG[49]证明了一般的N维空间中Fisher-KPP方程非平面行波解的稳定性:若摄动具有紧支集, 那么所有的(平面的和非平面的)行波解都是整体稳定的;若摄动没有紧支集但具有适当的指数衰减率,那么传播速度大于最小波速的那部分行波解是整体稳定的. 最近,El SMAILY等[50]考虑了二维周期剪切流中的非平面行波解. 证明了最小传播速度的存在性、行波解的单调性, 还分别讨论了反应项、扩散项和对流项对最小传播速度的影响. 前几节介绍的主要是方程(1)满足锥条件(3)的非平面行波解的一些结果,这些工作主要是由一些法国学者完成的.在这一节中,我们列出一些其他相关方程或方程组的非平面行波解的研究结果.TANIGUCHI等在Allen-Cahn方程的V状行波解和棱锥状行波解等方面做出了系列的工作, 包括这类非平面行波解的存在性、唯一性、单调性以及渐近稳定性等[36,51-55].此外, TANIGUCHI等还就平均曲率流方程中的非平面行波解问题做了一些研究, 例如考虑了行波解的分类以及旋转对称非平面行波解的存在性[56]; 考虑了平均曲率流方程非平面行波解的稳定性以及V状行波解的收敛性等解的长时间行为问题[57-59].近年来, 一些国内学者也开始关注非平面行波解的一些问题. 例如在柱状区域的反应扩散对流方程的非平面行波解,以及具时滞或周期的反应扩散方程及方程组的非平面行波解等方面取得了一系列深刻的研究成果[60-65].对周期或准周期区域中的平均曲率流方程的准周期行波解等问题做出了一系列的研究工作,给出了准周期行波及其平均速度的严格定义,并且证明了存在性、唯一性、稳定性还讨论了平均传播速度等问题[66-72]. 由于非线性反应扩散方程的非平面行波解是一类较新的问题,所以到目前为止,仍然有一些尚未解决的重要问题.特别是在部分方向上具有周期性的全空间中的相应问题.显然,通常的没有周期性的区域可以看成是周期性区域的周期趋于零时的特例.所以,在周期性区域中考虑非线性扩散方程的锥状行波解使得所考虑的问题更具有广泛性.此外,研究周期趋于零和周期趋于无穷大这2个极限过程将是特别有意义的问题.除了在周期性介质中非线性反应扩散方程的锥状行波解以外,在通常的没有周期性的区域中也还有一些重要的问题没有解决.例如,在N维空间中(N≥2),若摄动没有紧支集,那么由HAMEL和NADIRASHVILI所构造的这类具最小波速的行波解的稳定性依然是个公开问题. 此外, 这类由测度生成的解关于测度的唯一性也是一个公开的问题. [1] LUTHER R. Raumliche fortpflanzug chemister reaktionen[J].Z fur Zelktrochemie und angew Physikalische Chemie,1906,12(32):596-600. [2] FISHER R. The advance of advantageous genes[J]. Ann Eugenics, 1937, 7: 335-369. [3] KOLMOGOROV A, PETROVSKY I,PISKUNOV N. Etude de l’équation de la diffusion avec croissance de la quantité de matière et son applicationun problème biologique[J].Bulletin Université d’EtatMoscou (Bjul Moskowskogo Gos Univ), Série Internationale:Section A, 1937, 1: 1-26. [4] BUCKMASTER J, LUDFORD G. Lectures on mathematical combustion[M]∥CBMS-NSF Conf Series in Applied Math.Philadelphia,PA:Society for industrial and Applied Mathematics,1983. [5] BUCKMASTER J. The mathematics of combustion[M]∥Frontiers in Applied Mathematics.Philadelphia,PA:Society for industrial and Applied Mathematics,1985. [6] JOULIN G. Dynamique des fronts de flammes[R]∥Modélisation de la combustion, Images des Mathémati-ques. Paris: CNRS, 1996. [7] LEWIS B, VON ELBE G. Combustion, flames and explosions of gases[M]. New York, London:Academic Press,1961. [9] SIVASHINSKY G. The structure of Bunsen flames[M]. J Chem Phys, 1975, 62: 638-643. [10] SIVASHINSKY G. The diffusion stratification effect in Bunsen flames[J].J Heat Transfer, Transactions of ASME, 1974, 11: 530-535. [11] WILLIAMS F. Combustion theory[M]. New York:Addison-Wesley,1983. [12] ARONSON D, WEINBERGER H.Multidimensional nonlinear diffusions arising in population genetics[J].Adv Math, 1978, 30: 33-76. [13] BERESTYCKI H, NICOLAENKO B, SCHEURER B.Traveling waves solutions to combustion models and their singular limits[J].SIAM J Math Anal, 1985, 16: 1207-1242. [14] KANEL’ Y. Certain problems of burning-theory equations[J]. Sov Math Dokl, 1961, 2: 48-51. [15] BERESTYCKI H, LARROUTUROU B, LIONS P. Multidimensional traveling-wave solutions of a flame propagation model[J]. Arch Rat Mech Anal, 1990, 111: 33-49. [16] BERESTYCKI H, NIRENBERG L.Travelling fronts in cylinders[J]. Ann Inst H Poincaré, Anal Non Lin, 1992, 9: 497-572. [17] BERESTYCKI H, HAMEL F. Front propagation in periodic excitable media[J]. Comm Pure Appl Math, 2002, 55: 949-1032. [18] XIN J. Existence of planar flame fronts in convective-diffusive periodic media[J]. Arch Rat Mech Anal, 1992, 121: 205-233. [19] XIN J. Analysis and modeling of front propagation in heterogeneous media[J]. SIAM Review, 2000, 42: 161-230. [20] HAMEL F, MONNEAU R. Solutions of semilinear elliptic equations in RNwith conical-shaped level sets[J].Comm Part Diff Eq, 2000, 25: 769-819. [21] HAMEL F, MONNEAU R, ROQUEJOFFRE J-M.Existence and qualitative properties of multidimensional conical bistable fronts[J].Disc Cont Dyn Systems A, 2005, 13: 1069-1096. [22] BONNET A,HAMEL F. Existence of non-planar solutions of a simple model of premixed Bunsen flames[J].SIAM J Math Anal, 1999, 31: 80-118. [23] HARAGUS M, SCHEEL A.Corner defects in almost planar interface propagation[J].Ann Inst H Poincaré, Anal Non Linéaire, 2006, 23: 283-329. [24] BRAMSON M.Convergence of solutions of the Kolmogorov equation to travelling waves[J].Mem Amer Math Soc,1983,44(285):1-190. [25] FIFE P, MCLEOD J.The approach of solutions of non-linear diffusion equations to traveling front solutions[J].Arch Rat Mech Anal, 1977, 65: 335-361. [26] SATTINGER D.Stability of waves of nonlinear parabolic systems[J]. Adv Math, 1976, 22: 312-355. [27] SATTINGER D.Weighted norms for the stability of traveling waves[J].J Diff Equations, 1977, 25: 130-144. [28] BERASTYCKI H, LARROUTUROU B, ROQUEJOFFRE J-M.Stability of travelling fronts in a curved flame model, Part I: Linear analysis[J].Arch Rat Mech Anal, 1992, 117: 97-117. [29] MALLORDY J-F, ROQUEJOFFRE J-M.A parabolic equation of the KPP type in higher dimensions[J].SIAM J Math Anal, 1995, 26: 1-20. [30] ROQUEJOFFRE J-M.Stability of travelling fronts in a curved flame model, Part II: Non-linear orbital stability[J].Arch Rat Mech Anal, 1992, 117: 119-153. [31] ROQUEJOFFRE J-M. Convergence to travelling waves for solutions of a class of semilinear parabolic equation[J].J Diff Equations, 1994, 108: 262-295. [32] ROQUEJOFFRE J-M.Eventual monotonicity and convergence to travelling fronts for the solutions of parabolic equations in cylinders[J]. Ann Inst H Poincaré, Anal Non Linéaire, 1997, 14: 499-552. [33] LEVERMORE C, XIN J.Multidimensional stability of travelling waves in a bistable reaction-diffusion equation, II[J].Comm Part Diff Eq, 1992, 17: 1901-1924. [34] XIN J.Muldimensional stability of travelling waves in a bistable reaction-diffusion equation, I[J].Comm Part Diff Eq, 1992, 17: 1889-1899. [35] HAMEL F, MONNEAU R, ROQUEJOFFRE J-M.Stability of conical fronts in a combustion model[J].Ann Sci Ecole Normale Supèrieure, 2004, 37: 469-506. [36] NINOMIYA H, TANIGUCHI M.Existence and global stability of traveling curved fronts in the Allen-Cahn equations[J].J Diff Equations, 2005, 213: 204-233. [37] HAMEL F, MONNEAU R, ROQUEJOFFRE J-M.Asymptotic properties and classification of bistable fronts with Lipschitz level sets[J].Disc Cont Dyn Systems, 2006, 14: 75-92. [38] FIFE P.Dynamics of internal layers and diffusive interfaces[C]∥CBMS-NSF Regional Conference Series in Applied Mathematics. Philadelphia, PA:Society for industry and Applied Mathematics,1988. [39] HAMEL F, MONNEAU R, ROQUEJOFFRE J-M.Existence and qualitative properties of multidimensional conical bistable fronts[J].Disc Cont Dyn Systems A, 2005,13(4):1069-1096. [40] CHEN X, GUO J, HAMEL F,et al.Traveling waves with paraboloid like interfaces for balanced bistable dynamics[J]. 2007, 24: 369-393. [41] DE GIORGI E.Convergence problems for functionals and operators[C]∥Proc Int Meeting on Recent Methods in Nonlinear Analysis. Rome, 1978: 131-188. [42] SAVIN O.Regularity of flat level sets in phase transitions[J].Annals of Mathematics, 2009, 169(1): 41-78. [43] AMBROSIO L, CABRÉ X.Entire solutions of semilinear elliptic equations in R3and a conjecture of De Giorgi[J].J Amer Math Soc, 2000, 13: 725-739. [44] BERESTYCKI H, CAFFARELLI L, NIRENBERG L.Further qualitative properties for elliptic equations in unbounded domains[J].Ann Scuola Norm Sup Pisa Cl Sci, 1997, 25: 69-94. [45] GHOUSSOUB N, GUI C.On a conjecture of De Giorgi and some related problems[J].Math Ann, 1998, 311: 481-491. [46] FIFE P.Mathematical aspects of reacting and diffusing systems[M]∥Lecture Notes in Biomathematics. Berlin, New York: Springer Verlag, 1979. [47] HADELER K, ROTHE F.Travelling fronts in nonlinear diffusion equations[J].J Math Biology, 1975, 2: 251-263. [48] HAMEL F, NADIRASHVILI N.Travelling waves and entire solutions of the Fisher-KPP equation in RN[J].Arch Rat Mech Anal, 2001, 157: 91-163. [49] HUANG R.Stability of travelling fronts of the Fisher-KPP equation in RN[J].Nonlinear Differ Equ Appl, 2008, 15: 599-622. [50] EL SMAILY M, HAMEL F, HUANG R.Two-dimensional curved fronts in a periodic shear flow[J].Nonlinear Analysis, 2011, 74: 6469-6486. [51] KUROKAWA Y,TANIGUCHI M.Multi-dimensional pyramidal travelling fronts in the Allen-Cahn equations[J].Proceedings of the Royal Society of Edinburgh, 2011, 141A: 1031-1054. [52] NINOMIYA H,TANIGUCHI M.Global stability of traveling curved fronts in the Allen-Cahn equations[J].Discrete and Continuous Dynamical Systems, 2006, 15: 819-832. [53] TANIGUCHI M.Traveling fronts of pyramidal shapes in the Allen-Cahn equations[J].SIAM J Math Anal, 2007, 39: 319-344. [54] TANIGUCHI M.The uniqueness and asymptotic stability of pyramidal traveling fronts in the Allen-Cahn equations[J].J Differential Equations, 2009, 246: 2103-2130. [55] TANIGUCHI M.Multi-dimensional traveling fronts in bistable reaction-diffusion equations[J].Discrete and Continuous Dynamical Systems:Ser A, 2012, 32: 1011-1046. [56] NINOMIYA H,TANIGUCHI M.Traveling curved fronts of a mean curvature flow with constant driving force[M]∥Free Boundary Problems: Theory and Applications I, Mathematical Sciences and Applications, 2000, 13: 206-221. [57] NINOMIYA H,TANIGUCHI M.Stability of traveling curved fronts in a curvature flow with driving force[J].Methods and Applications of Analysis, 2001, 8: 429-450. [58] NINOMIYA H,TANIGUCHI M.Stability of a traveling wave in curvature flows for spatially non-decaying initial perturbations[J].Discrete Cont Dyn S, 2006, 14: 203-220. [59] NINOMIYA H,TANIGUCHI M.Convergence to V-shaped fronts in curvature flows for spatially non-decaying initial perturbations[J].Discrete Cont Dyn S, 2006, 16: 137-156. [60] LI W, LIU N, WANG Z.Entire solutions in reaction-advection-diffusion equations in cylinders[J].J Math Pures Appl, 2008, 90: 492-504. [61] LIU N, LI W, WANG Z.Entire solutions of reaction-advection-diffusion equations with bistable nonlinearity in cylinders[J].J Differential Equations, 2009, 246: 4249-4267. [62] LIU N, LI W, WANG Z.Pulsating type entire solutions of monostable reaction-advection-diffusion equations in periodic excitable media[J].Nonlinear Anal, 2012, 75: 1869-1880. [63] SHENG W, LI W, WANG Z.Periodic pyramidal traveling fronts of bistable reaction-diffusion equations with time-periodic nonlinearity[J].J Differential Equations, 2012, 252: 2388-2424. [64] WANG Z.Traveling curved fronts in monotone bistable systems[J].Discrete Contin Dyn Syst, 2012, 32: 2339-2374. [65] WANG Z, WU J.Periodic traveling curved fronts in reaction-diffusion equation with bistable time-periodic nonlinearity[J].J Differential Equations, 2011, 250: 3196-3229. [66] LOU B. Periodic rotating waves in an undulating annulus and their homogenization limit[J].SIAM J Math Anal, 2006, 38: 693-716. [67] LOU B.Periodic travelling wave solutions of a curvature flow equation in the plane[J].Tohoku Math J, 2007, 59: 365-377. [68] LOU B.Periodic rotating waves of a geodesic curvature flow on the sphere[J].Comm Partial Differential Equations, 2007, 32: 525-541. [69] LOU B.Periodic traveling waves of a mean curvature flow in heterogeneous media[J].Discrete Contin Dyn Syst, 2009, 25: 231-249. [70] LOU B, CHEN X.Traveling waves of a curvature flow in almost periodic media[J].J Differential Equations, 2009, 247: 2189-2208. [71] LOU B.Spiral rotating waves of a geodesic curvature flow on the unit sphere[J].Discrete Contin Dyn Syst: Ser B, 2012, 17: 933-942. [72] MATANO H, NAKAMURA K, LOU B.Periodic traveling waves in a two-dimensional cylinder with saw-toothed boundary and their homogenization limit[J].Netw Heterog Media, 2006, 1(4): 537-568. Keywords: reaction-diffusion equations; nonplanar; travelling fronts NonplanarTravellingFrontsofReaction-DiffusionEquationsinRN HUANG Rui,YIN Jingxue* (School of Mathematical Sciences, South China Normal University, Guangzhou 510631, China) The problems about the nonplanar travelling fronts of reaction-diffusion equations in RNare proposed by some French researchers who have obtained many important results in recent ten years. Some main results about these issues are reviewed. Firstly, as an example of nonplanar travelling fronts, the model of Bunsen flame is introduced. The PDE model of this problem with two important nonlinear sources, that is, ignition temperature source and bistable source which have obvious reality background is given accordingly. Then, some qualitative properties of these nonplanar travelling fronts, including the existence, the uniqueness, the monotonicity, the stability and the properties of the level sets of the solutions are reviewed. Next, the results about the equation with KPP type source, including the existence of an infinite-dimensional manifold of nonplanar fronts, the monotonicity, the stability and the properties of minimal propagation speed are introduced. At last, some other relative results in this field are reviewed and then some open questions in this subject are proposed. 2012-10-12 国家自然科学基金项目(11071099,11001103);高等学校博士学科点专项科研基金项目(20114407110008);教育部留学回国人员科研启动基金(教外司留[2009]1341) *通讯作者:尹景学,教授,长江学者,Email: yjx@scnu.edu.cn. 1000-5463(2013)01-0001-09 O175.29 A 10.6054/j.jscnun.2012.12.001 【中文责编:庄晓琼 英文责编:肖菁】









3 非平面行波解的存在性








4 Fisher-KPP方程的行波解



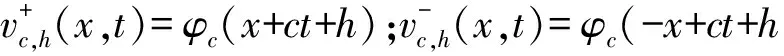















5 其他相关研究
