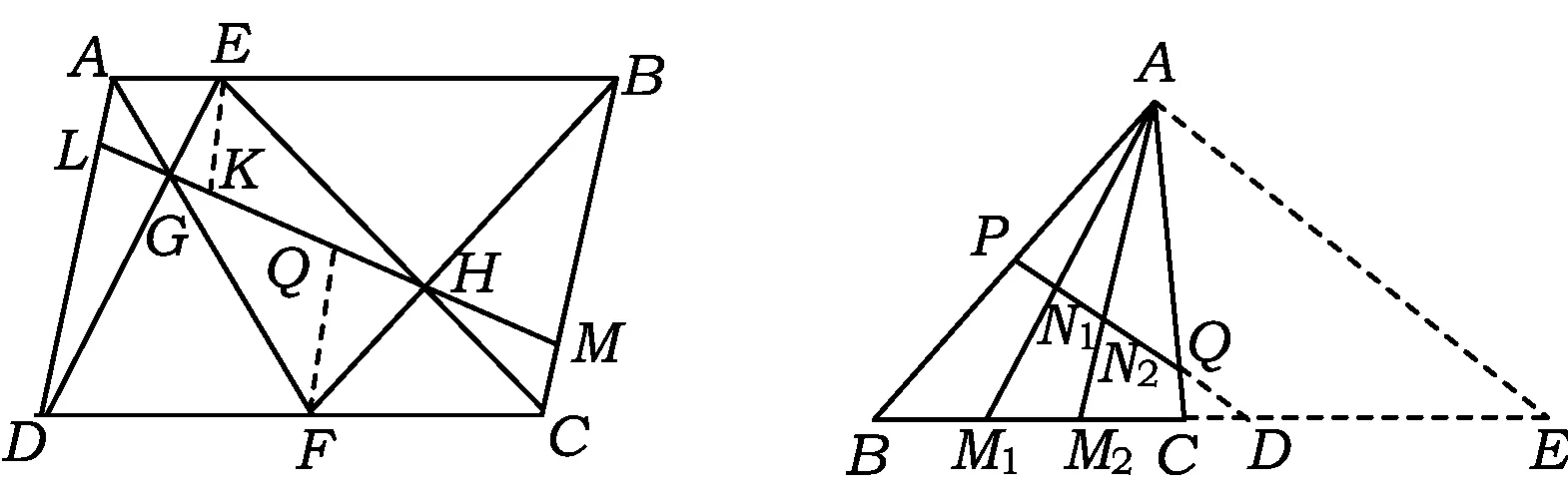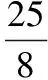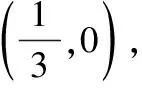初中数学竞赛训练题

2013-10-26

中学教研(数学) 2013年6期

关键词：半圆正整数过点

初中数学竞赛训练题

一、填空题

1．用[x]表示不大于x的最大整数，则方程x2-2[x]-3=0的解为______．

2．小王沿街匀速行走，发现每隔6分钟从背后驶过一辆18路公交车，每隔3分钟从迎面驶来一辆18路公交车．假设每辆18路公交车行驶速度相同，而且18路公交车总站每隔固定时间发一辆车，那么发车间隔的时间是______分钟．

(2008年全国初中数学联赛试题)

3．设整数a使得关于x的一元二次方程5x2-5ax+26a-143=0的2个根都是整数，则a的值为______．

(2008年浙江省初中数学竞赛试题)

4．使得5×2m+1是完全平方数的整数m的个数为______．

(2012年全国初中数学联赛试题)

5．已知n是偶数，且1≤n≤100．若有唯一的正整数对(a,b)使得a2=b2+n成立，则这样的n的个数为______．

6. 图1中共有多少个三角形？

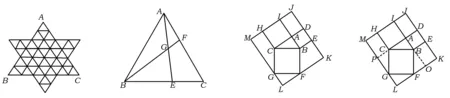
图1 图2 图3 图4

8.勾股定理是几何中的一个重要定理，在我国古算书《周髀算经》中就有“若勾三，股四，则弦五”的记载，如图3是由边长相等的小正方形和直角三角形构成的，可以用其面积关系验证勾股定理.图4是由图3放入矩形内得到的，∠BAC=90°,AB=3,AC=4.点D,E,F,G,H,I都在矩形KLMJ的边上，则矩形KLMJ的面积为______．

图5 图6

9．如图5，d菱形ABCD中，AB=2，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为______．

10．如图6，∠AOB=60°，点P在∠AOB的角平分线上，OP=10 cm,点E,F是∠AOB边OA,OB上的动点，当△PEF的周长最小时，点P到EF距离是______.

二、解答题

(2010年天津市初中数学竞赛试题)

12．(1)证明：存在整数x,y满足x2+4xy+y2=2 022.

(2)问：是否存在整数x,y满足x2+4xy+y2=2 011?证明你的结论．

(2011年上海市初中数学竞赛试题)

13．已知正整数a满足192|(a3+191),且a<2 009，求满足条件的所有可能的正整数a的和．

14．若正整数a，b满足：a-b是素数，且ab是完全平方数. 当a≥2 012时，求a的最小值．

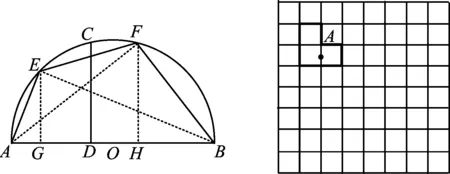
图7 图8

15. 如图7，AB为半圆直径,D为AB上一点,分别在半圆上取点E,F,使EA=DA,FB=DB.过点D作AB的垂线,交半圆于点C.求证：CD平分EF.

16 四边形ABCD是一个平行四边形，E是AB上的一点，F为CD上一点．AF交ED于点G，EC交FB于点H．联结GH并延长交AD于点L，交BC于点M，求证：DL=BM.

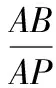
18. 平面上n个圆最多能把平面分成多少个部分？

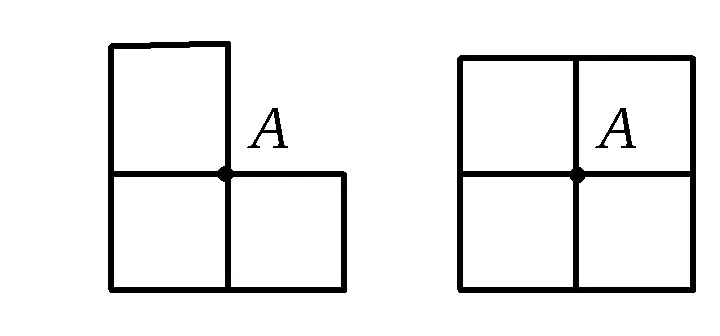
19. 在8×8的方格棋盘中，取出一个由3个小方格组成的“L”形(如图8)，一共有多少种不同的方法？

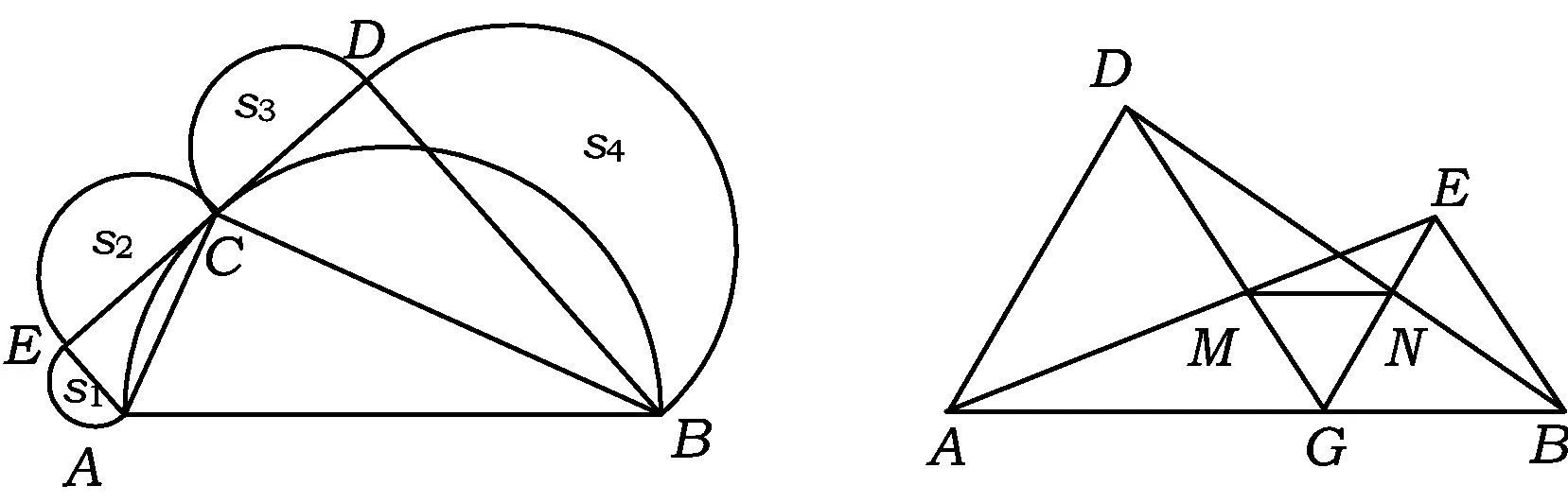
图9 图10

20.如图9，以AB为直径作半圆交直角梯形ABED另一腰DE于点C，再分别以AE,CE,CD,BD为直径作半圆．若AC=3,BC=4,求S1,S2,S3,S4的面积和．

21.在平面直角坐标系中，矩形OACB的顶点O在坐标原点，顶点A,B分别在x轴、y轴的正半轴上，OA=3，OB=4，D为边OB的中点.

(1)若E为边OA上的一个动点，当△CDE的周长最小时，求点E的坐标；

(2)若E,F为边OA上的2个动点，且EF=2，当四边形CDEF的周长最小时，求点E,F的坐标.

22．如图10，点C是线段AB上的任意一点(点C不与点A,B重合)，分别以AC,BC为边在直线AB的同侧作等边△ACD和等边△BCE，AE与CD相交于点M，BD与CE相交于点N．

(1)求证：MN∥AB.

(2)若AB的长为10 cm，当点C在线段AB上移动时，是否存在这样的一点C，使线段MN的长度最长?若存在，请确定点C的位置并求出MN的长；若不存在，请说明理由．

参考答案

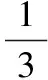
整理得

ab-6(a+b)+18=0,

即

(a-6)(b-6)=18.

由a,b均为正整数，不妨设a

(a-6,b-6)=(1,18),(2,9),(3,6),

于是(a,b,c)=(7,24,25)，(8,15,17),(9,12,15).

因此满足条件的直角三角形3条边长分别为(7,24,25)，(8,15,17)和(9,12,15)．

12．证明(1)x=43,y=1满足

x2+4xy+y2=2 022．

(2)由x2≡0,1(mod4)，y2≡0,1(mod4)，得

x2+4xy+y2≡0,1,2(mod4).

又2 011≡3(mod4)，因此不存在满足x2+4xy+y2=2 011的整数x,y．

13．解由192|(a3+191)可得

192|(a3-1)，

而192=3×26，且

a3-1= (a-1)[a(a+1)+1]=

(a-1)a(a+1)+(a-1).

a=192k+1，

又0

11+192(1+2+……+10)=10 571．

14．解设a-b=m(m是素数)，ab=n2(n是自然数，n≥1).因为 (a+b)2-4ab= (a-b)2，所以

(2a-m)2-4n2=m2，

即

(2a-m+2n)(2a-m-2n) =m2.

因为2a-m+2n与2a-m-2n都是正整数，且2a-m+2n>2a-m-2n(m为素数)，所以

2a-m+2n=m2，2a-m-2n=1,

解得

于是

由m是素数，得m≥89. 此时

当a=2 025时，m=89,b=1 936，n=1 980,此时，a的最小值为2 025.

15.证明如图7,分别过点E,F作AB的垂线,点G,H为垂足,联结FA,EB.易知

DB2=FB2=AB·HB,

AD2=AE2=AG·AB,

得

DB2-AD2=AB(HB-AG),

即

(DB-AD)AB=AB(HB-AG),

于是

DB-AD=HB-AG,

即

DB-HB=AD-AG,

得

DH=GD.

而EG∥CD∥FH，故CD平分EF.

图11 图12

16.证明如图11，过点E,F分别作EK∥AD，FQ∥AD，则

从而

AL·DL=QF·EK，

同理可得

CM·MB=QF·EK,

故

AL·DL=CM·MB.

又因为AL+DL=CM+MB，所以DL=BM.

17.证明如图12,若PQ∥BC,易证结论成立.

若PQ与BC不平行，延长PQ交直线BC于点D.过点A作PQ的平行线交直线BC于点E，可得

又由BM1=CM2,可知BE+CE=M1E+M2E，于是

18.解1个圆最多能把平面分成2个部分；2个圆最多能把平面分成4个部分；3个圆最多能把平面分成8个部分；现在加入第4个圆，为了使分成的部分最多，第4个圆必须与前面3个圆都有2个交点．因此得6个交点，这6个交点将第4个圆的圆周分成6段圆弧，而每一段圆弧将原来的部分一分为二，即增加了一个部分，于是，4个圆最多将平面分成8+6=14个部分．

同理，5个圆最多将平面分成14+8=22个部分．类似上面的方法，可以计算出n个圆最多分平面的部分数为:

2+1×2+2×2+…+(n-1)×2=

2+2[1+2+…+(n-1)]=n2-n+2．