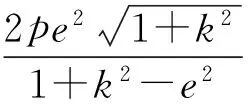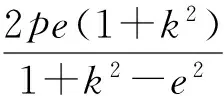乾坤挪移二合一 弦长化减理相通 论定特方破难关——2012年江苏省数学高考第19题简解

●

(六合区程桥高中 江苏南京 211504)

乾坤挪移二合一弦长化减理相通论定特方破难关
——2012年江苏省数学高考第19题简解

●王安寓

(六合区程桥高中 江苏南京 211504)

2012年江苏省数学高考第19题,网上评论很多,褒贬不一.面对这道计算繁杂的题目,如何化难为简、化陌生为熟悉？如何突破命题人设置的关卡，找到问题的本质快速解题？

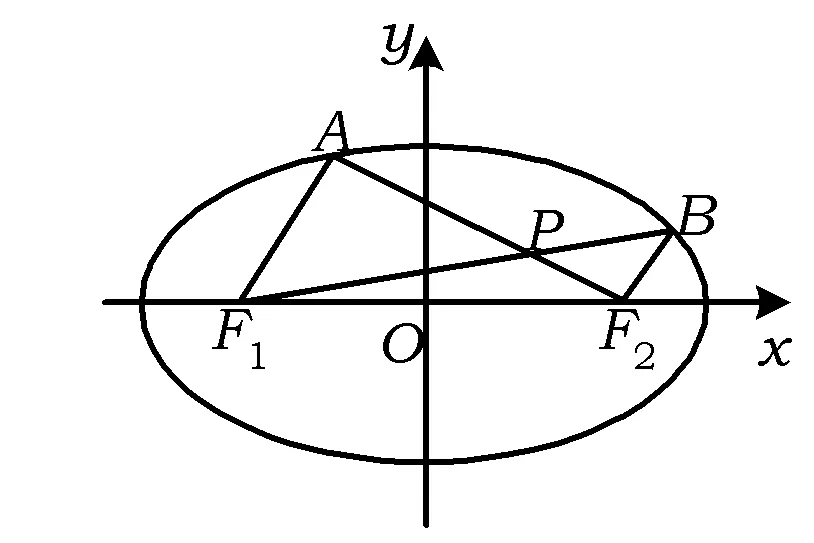
图1

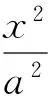
(1)求椭圆的方程.

(2)设A,B是椭圆上位于x轴上方的2个点，且直线AF1与直线BF2平行，AF2与BF1交于点P．

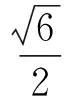
②求证：PF1+PF2是定值．

本题主要考查直线与椭圆的相关知识，考查运算能力和推理能力.本题构思新颖，设问独特(在合理处设置不合理的问法)，考查学生活用数学知识的能力，体现重思维的命题理念.合理运用椭圆的对称性转化题设条件，将2条平行线转移到一条上，必有利于解题.本文就此作一点探讨.

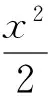
1 乾坤挪移二合一，弦长化减理相通

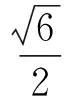
由此可以看出，该题实际上是常见题目的逆向命题.我们常见的题目是:给定椭圆和过焦点的直线,求弦长CF2+BF2或CF2-BF2,即直线斜率k为定值,则弦长CF2+BF2或CF2-BF2也为定值(常规思路是联立方程组,利用韦达定理和弦长公式).反之，CF2-BF2为定值,则直线斜率k为定值；弦长CF2+BF2为定值，则求直线的斜率k可能有正、负2个值.这恰好是常见题目的逆向.如何解决呢?还是需要常规思路.设出直线方程,联立方程组,利用弦长公式构造关于k的方程求解即可.

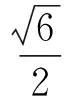
当BC斜率不存在时,显然不合题意.当BC的斜率存在时,设BC的方程为

y=k(x-1),

设B(x1,y1),C(x2,y2)，联立并消去y，用韦达定理得

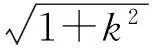
解得

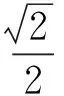
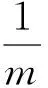
2 乾坤挪移二合一，数形结合显奇迹

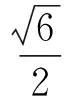
图2

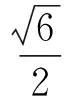
过点B,C分别作椭圆右准线l:x=2的垂线,垂足分别为M,N,过点B作BS⊥CN于点S,则

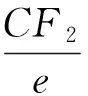
欲求斜率k,只需求BC(在△BCS中,k=tan∠BCS).已知结论

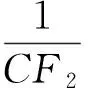
即

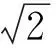
又

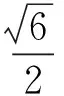
即

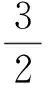
从而

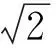
解得

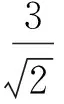
因此

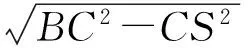
即

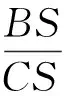
评注数与形完美结合,让人赏心悦目.该题的几何解释很美,解法2用漂亮的图解决该问题：给定斜率k,求CF2-BF2.

为叙述方便,设CF2=n,BF2=m,则

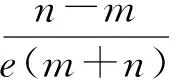
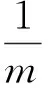
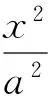
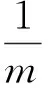
(证明略.)

3 运用结论和定义，消除差异破难关

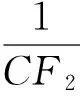
(2)②证法1延长BF2,交椭圆于另一点C.因为AF1∥BF2,所以由椭圆的对称性,知AF1=CF2,则

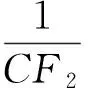
即

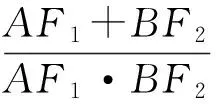
因为AF1∥BF2,所以

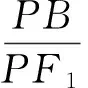
即

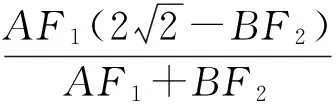
同理可得

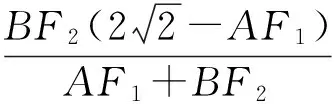
因此

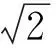
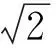
即PF1+PF2是定值.

4 运用特值来探路，构建方程破难关

由待证结论联想到椭圆的定义，即证明点P在某椭圆上.为寻求该椭圆方程(目标意识)，可先从特例入手，求出椭圆的方程，再证明点P适合椭圆方程，即证得PF1+PF2是定值.

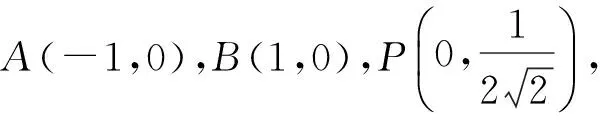
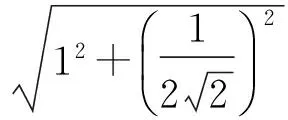
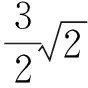
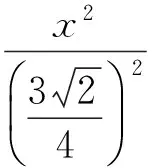
即

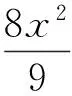
下面证明动点P适合上述椭圆方程.设B(x1,y1),C(x2,y2),则A(-x2,-y2),

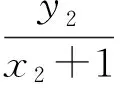
联立得点P的坐标满足

设BC:x=my+1,代入椭圆方程，由韦达定理得

从而

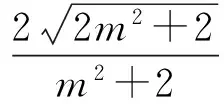
此时

消去m，得

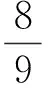
因此点P在椭圆上,即

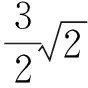
评注证法2与常规的圆锥曲线题目相仿:设出直线方程,联立方程组,利用韦达定理,代入计算,有一种熟悉感.另外，证法2采用“先猜后证”的解题方法，有的放矢，目标明确，但运算量稍大.

5 圆锥曲线三兄弟，类比拓展寻共识

经过上述研究,我们得到如下结论.

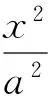
(1)若直线AF1的斜率不存在,则

BF2-AF1=0;

若直线AF1的斜率存在(为k),则

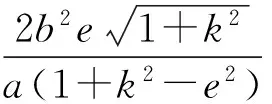
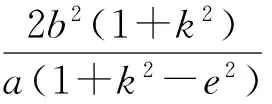
(2)若BF2-AF1=0,则直线AF1的斜率不存在;

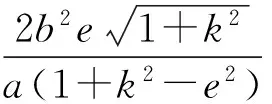
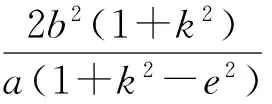
结论3同结论2的条件,设直线AF2,BF1交于点P,则点P的轨迹方程为

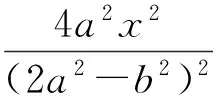
即

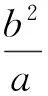
对于双曲线有类似结论.

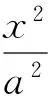
(1)若直线AF1的斜率不存在,则BF2-AF1=0;

若直线AF1的斜率存在(为k),则

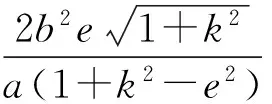
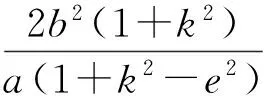
(2)若BF2-AF1=0,则直线AF1的斜率不存在;

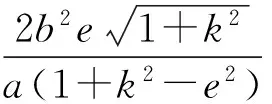
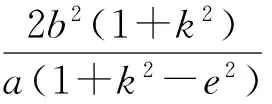
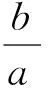
结论5同结论4的条件,设直线AF2,BF1交于点P,则点P的轨迹方程为

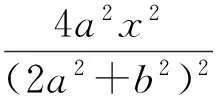
即

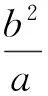
对于抛物线,也有类似结论.

结论6抛物线y2=±2px(p>0)的左、右焦点分别为F1,F2,过焦点F1,F2分别作相互平行的直线AF1,BF2,与抛物线的x轴同侧部分交于点A,B，则

(1)若直线AF1的斜率不存在,则BF2-AF1=0;

若直线AF1的斜率存在(为k),则

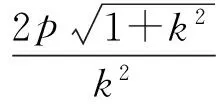
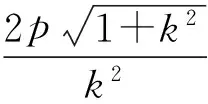
(2)若BF2-AF1=0,则直线AF1的斜率不存在;

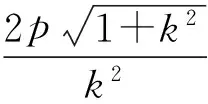
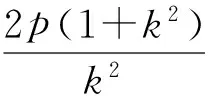
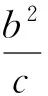
结论7F1,F2是圆锥曲线(抛物线取2个)的左、右焦点,过F1,F2分别作相互平行的直线AF1,BF2,与曲线x轴同侧部分交于点A,B,e为离心率,则

(1)若直线AF1的斜率不存在,则BF2-AF1=0;

若直线AF1的斜率存在(为k),则

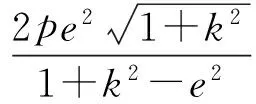
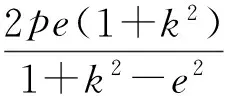
(2)若BF2-AF1=0,则直线AF1的斜率不存在;