不愤不启 不悱不发——“与抛物线切线有关的问题”课例及点评

●

(东阳中学 浙江东阳 322100)

不愤不启不悱不发——“与抛物线切线有关的问题”课例及点评

●傅红玲吴国建

(东阳中学 浙江东阳 322100)

在“金华市数学高考复习研讨会”中，笔者上了一节题为“与抛物线切线有关的问题”的教研课，为此历经一个从选题到反思的心路历程，现将课例呈现给同行，谨请批评指正．

1 选“课题”的“变变变”过程

教研课课题：任选“圆锥曲线的综合问题”中的一个点.圆锥曲线综合问题涉及面广，要选择一个能体现解析几何重点和高考热点，并且通过一节课能让这个点有完整体现的课题确实不易.几经周折，最后选定近几年高考题中出现较多的“以抛物线切线为载体的直线与圆锥曲线的位置关系问题”为基点的课题：与抛物线切线有关的问题，针对“直线与抛物线的位置关系”作进一步深入探究．

2 选“题目”的“变变变”过程

本课的题目选自近几年高考题和模拟题，第一轮选题时，笔者准备了7个原始的高考题，经试讲发现：读题、求解析式花费时间太多，导致整堂课容量小，思想不能体现．因此第2轮选题时精简题目，砍掉了与课题无关的小题，课题突出了，但整体感觉就一节课围绕知识点做了几个例题，只是熟悉了知识点，而没有体现数学思想.最后确定题目形式:以一个高考题为母题，其余以变题的形式呈现，用统一的抛物线形式，真正地把“读题、求解析式”的时间让路给“探究、思考”，让学生的思维训练时间得到进一步保证.通过问题变式形式，环环相扣，层层深入，贯彻“把课堂交还给学生，让学生的思维火花闪耀”的教学理念．

3 课堂过程简录——变式教学

整个课堂设计：采用探究式教学法，借助多媒体辅助，通过“问题导入—导疑—导研——导练—导评”5个环节，完成以下教学目标：(1)掌握以抛物线的切线为载体的直线和圆锥曲线综合问题；(2)培养利用、挖掘、整合信息的能力；(3)通过问题变式得到一些漂亮的结论，激发学生探索的欲望，提升学习和研究的兴趣．

3.1 问题导入,激活思维

师:今天非常高兴能有这个机会，和同学们共同探究“与抛物线切线有关的问题”．先来复习：如何求抛物线的切线方程？

例1已知抛物线C:x2=4y，求在点Q(x0,y0)处的切线方程.

生:利用导数先求切线的斜率，再用点斜式写出切线方程．

(出示幻灯片.)

师:还有其他方法求斜率吗？

生:待定系数法设出方程，再用Δ=0求切线的斜率．

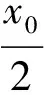
点评从试讲到上课情况看，特别是文科生大多选择利用导数求斜率．

3.2 问题导疑,激发兴趣

例2已知抛物线C:x2=4y，过抛物线外一点Q(x0,y0)作2条切线QA,QB,设切点为A,B.

师:设切点为A(x1,y1)，B(x2,y2),能否用类比的思想，写出切线QA,QB的切线方程？

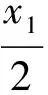
师:非常好！如图1，现在联结切点A,B,能用点Q表示弦AB吗?请大家尝试着完成．

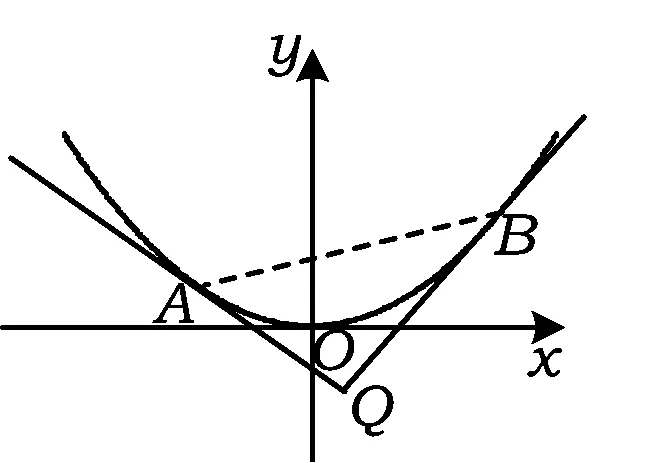
图1

问题1求过切点的弦AB所在的直线方程.

思考2分钟后，发现学生不能很清晰地整理解题思路,继续点拨.

师：联系点Q与弦AB的桥梁是切线方程，点Q与切线方程有什么关系？能否利用切线方程求出弦所在的方程？请继续尝试．

生:点Q代入切线方程得

即

从而

即

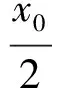
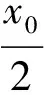
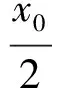
点评此处，点A既在弦AB上，又在切线上，同时还在抛物线上.当资源较多的时候，一定要学会信息的筛选和整合．

笔者把图中切线方程中的点A(x1,y1),B(x2,y2)改变颜色，突出这2个点坐标的作用.

师：观察2个切线方程，结构上有何共同之处？

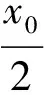
点评这一步环节学生求解困难比较大，需要点拨启发，甚至是启而不发，教师要耐心给学生充分的思考时间，要启发到位.最后要点出2个方程的不同之处，强调形似神不似．

3.3 问题导研,层层推进

图2

师:若点Q为准线上任意一点，弦AB会有什么特殊性质呢？会恒过焦点F吗？

大胆猜想，尝试着证明．

问题2已知点Q在准线l:y=-1上，证明：弦AB过焦点F.

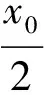
师:若弦AB过焦点F，2条切线的交点Q会在什么位置呢？

请同学们大胆的猜想,并完成下列问题．

问题3已知弦AB过焦点F，求2条切线的交点Q的轨迹方程．

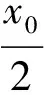
点评弦AB过抛物线的焦点⟺2条切线的交点在抛物线的准线上．

师:对于这种特殊位置对应的抛物线的2条切线有什么特殊的性质呢？请同学们大胆猜想，先从图像上观察，猜想2条切线可能的位置关系.

生:垂直．

师:进一步通过特殊点来验证.

生:垂直．

师:针对一个开放的数学问题,先通过猜想,再验证,最后一定要用严密的数学推理来证明.将本结论推广到一般情况．

采用指数平滑法的二次指数平滑法对当日已知负荷进行超短期负荷预测，结果记为y2。二次指数平滑法是用线性关系去拟合数据变化趋势，相比于一次指数平滑法精度有所提高，相对于三次及高次指数平滑法运算量小、计算简单。

问题4若弦AB过焦点F,判断2条切线是否垂直？并给出证明.

(本题条件较多，可以从多个角度、多种方法来思考，教师要给学生充分的思考空间.)

师:哪位同学来整理下解题思路？

师生合作:设切点为A(x1,y1)，B(x2,y2),则

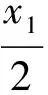
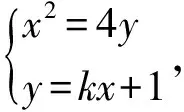
x2-4kx-4=0,

从而

x1x2=-4,

于是

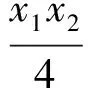
因此QA⊥QB(完整板书).

师:还有其他方法吗？

生:弦AB是过焦点的弦，因此借助于抛物线的定义，用平面几何和解析几何结合完成(用幻灯片直接投影)．

师生合作:前面几种方法都从弦AB出发，把点Q看成2条切线的交点，即终结点.换种角度来思考:把2条切线的交点作为起始点,再观察切线QA与QB，它们是对称的，可否从设切线方程入手？

解由Q(x0,-1),可设切线QA：y+1=k(x-x0),代入得

x2-4kx+4kx0+4=0,

利用

Δ=16k2-4×4(x0k+1)=0,

得

k2-x0k-1=0,

从而

k1·k2=-1．

点评引导本题时，体现的思想方法是：先借助于图像进行粗略判断，再进一步借助于特殊点进行验证，最后用数学思想方法进行严密证明，从而得到结论.这种思想方法，特别是对开放题会有明显的效果.本题的条件多样，如何更有效整合利用这些信息，就显得更加重要．

3.4 问题导练,及时反馈

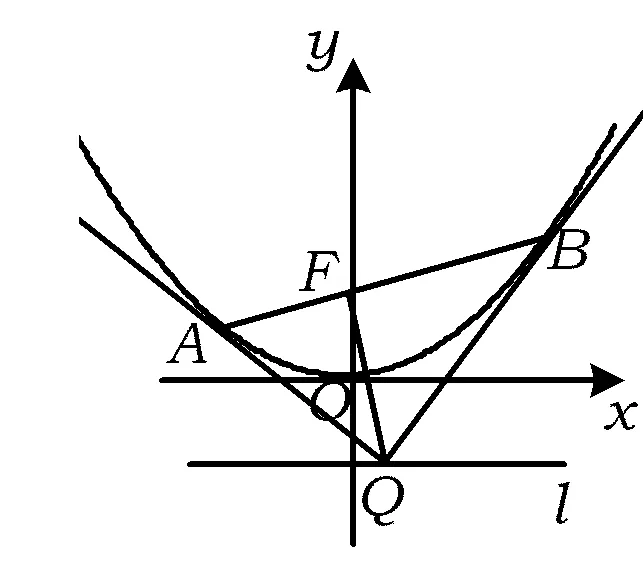
图3

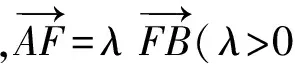
(学生板演.)

解法1

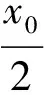
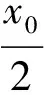
于是

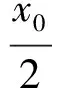
点评解法1利用了点Q的坐标，解法2利用了弦AB的直线方程，2位学生都充分利用本堂课得到的结论，很顺利地完成了解题.让学生动起来,从中享受结论带来的方便.

3.5 问题导评,整合提高

师：通过大家的共同努力，这堂课得到了几个漂亮的结论:

(1)在点Q(x0,y0)处的切线方程为

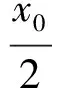
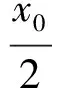
(2)弦AB过抛物线的焦点⟺2条切线的交点在抛物线的准线上⟺2条切线互相垂直.

师：这些结论是在给定一个具体的抛物线时得到的,请同学们课后进一步去探究：对于一般情况，这些结论是否依然成立？与抛物线有关的切线还有很多漂亮的结论，希望同学们能运用已有的信息，整合新的资料，大胆地猜想并利用严密的数学推论得到新的结论．

4 课后点评

本堂课是圆锥曲线综合课，首先题目选得合适，“与抛物线切线有关的问题”的口子虽然小,但是非常值得研究；其次是上得好课，采用问题导学的探究式教学，真正地把课堂还给学生，且问题设计得非常好，逐步提升思维深度，一环扣一环，层层深入，结构清晰，节奏明快，并在问题4中达到一个高潮，4种解法反应出学生的高水平,能从不同角度思考问题，也能很好地利用得到的结论，从讲解到提问到板演,整个课堂掌控良好．课堂氛围较好，教师有亲和力，很有耐心.一是给出充分的时间让学生探究;二是学生回答不出时耐心地引导和等待，充分肯定学生;三是走到学生中去，密切关注学生的答题情况，真正体现了以学生为主体的思想．

5 课后反思

本堂课集合数学组的整体力量，基本达成初定目标，但依然留有很多遗憾：

(1)知识层面：在探究问题3时，笔者备课时还准备了交轨法，用交点的思想求点Q的坐标，利用韦达定理完成，在本节课中未能用上．

若能引导学生想到下列解法：把点Q点看成2条切线的起始点，或把点Q看成2条切线的交点，即终止点，则可以从不同角度思考问题，充分挖掘信息，开阔学生思考问题的角度，进一步提升整合信息和挖掘信息的能力．

(2)教学引导层面：在问题4探究第4种方法的过程中，整个过程基本上是笔者在主导，其实可以更相信学生，更大尺度地放手让学生探究．

[1] 李锋,于海龙,童嘉森.抛物线的切线及其性质初探[J].高中数理化，2011(21)：9-10.

[2] 林国夫.抛物线中精彩的一点一线[J].中学数学:高中版,2010(9):50-51.