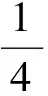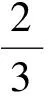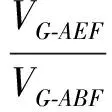自主招生中的立体几何问题
2013-10-26
●
(松阳县第一中学 浙江松阳 323400)
自主招生中的立体几何问题
●李玉梅
(松阳县第一中学 浙江松阳 323400)
立体几何试题是考查空间想象能力最好的载体.在自主招生试题中,这部分内容主要考查空间图形中线面的位置关系以及空间角、距离的计算,解题时往往将空间问题转化为平面问题来解决,体现数学中的转化与化归思想.另外,建立空间直角坐标系,将几何元素之间的关系数量化,可以看出用空间向量来解题的优势.本文主要谈谈自主招生中的立体几何问题.
1 求角的问题
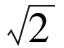
( )
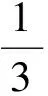
(2011年清华大学等七校联考试题)
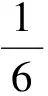
评注本题也可以平移DM与AN共面,即点M移到点N,点D移到CD的中点Q,或平移AN与DM共面,亦即点A移到点M,点N移到PN的中点Q,平移是解决线线问题的基本方法.
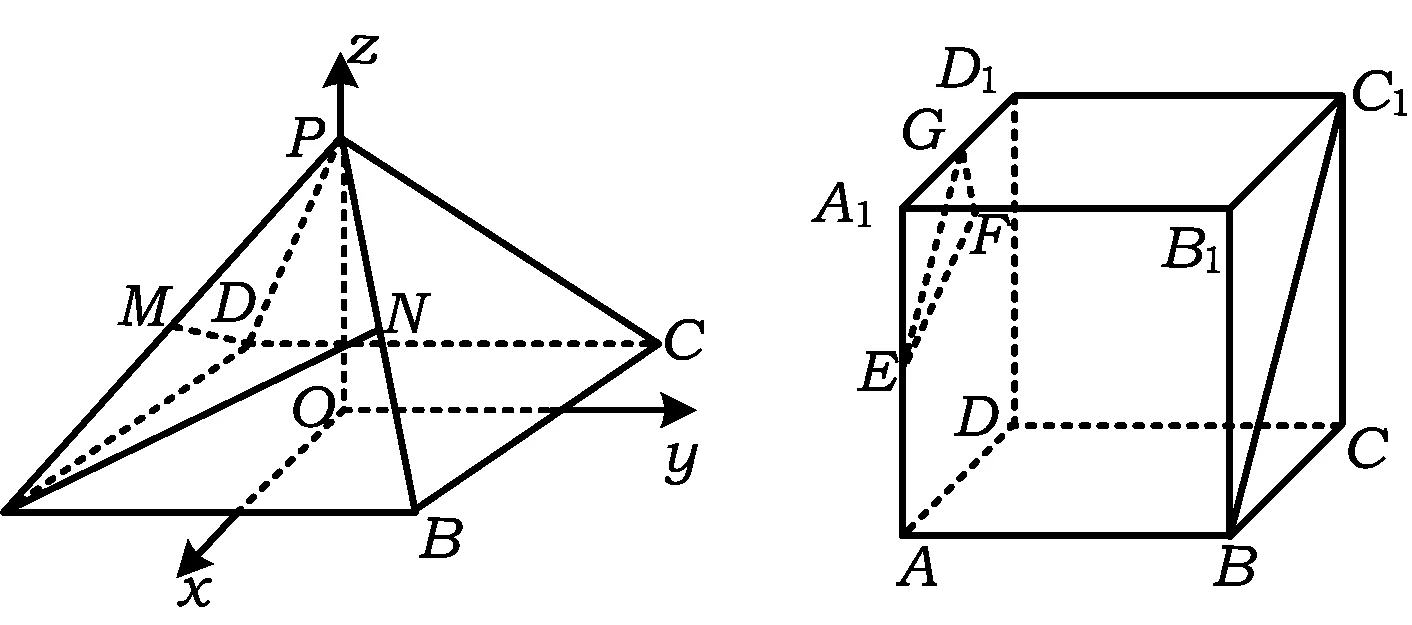
图1 图2
例2在正方体ABCD-A1B1C1D1中,E为棱AA1的中点,F是棱A1B1上的点,且A1F∶FB1=1∶3,则异面直线EF与BC1所成角的正弦值为
( )
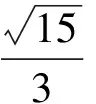
(2011年同济大学等九校联考试题)
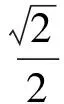
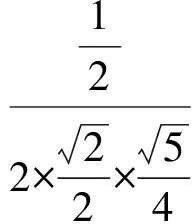
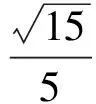
评注“线线角”问题的常用方法是平移法,此题也可以用坐标法求解.
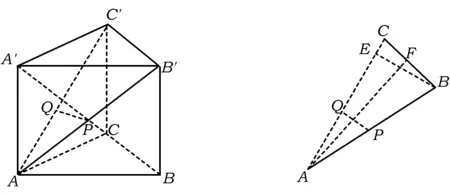
例3三棱柱ABC-A′B′C′的底面是边长为1的正三角形,高AA′=1,在AB上取一点P,设△PA′C′与底面的二面角为α,△PB′C′与底面的二面角为β,则tan(α+β)的最小值是
( )
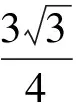
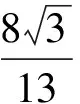
(2009年复旦大学自主招生试题)
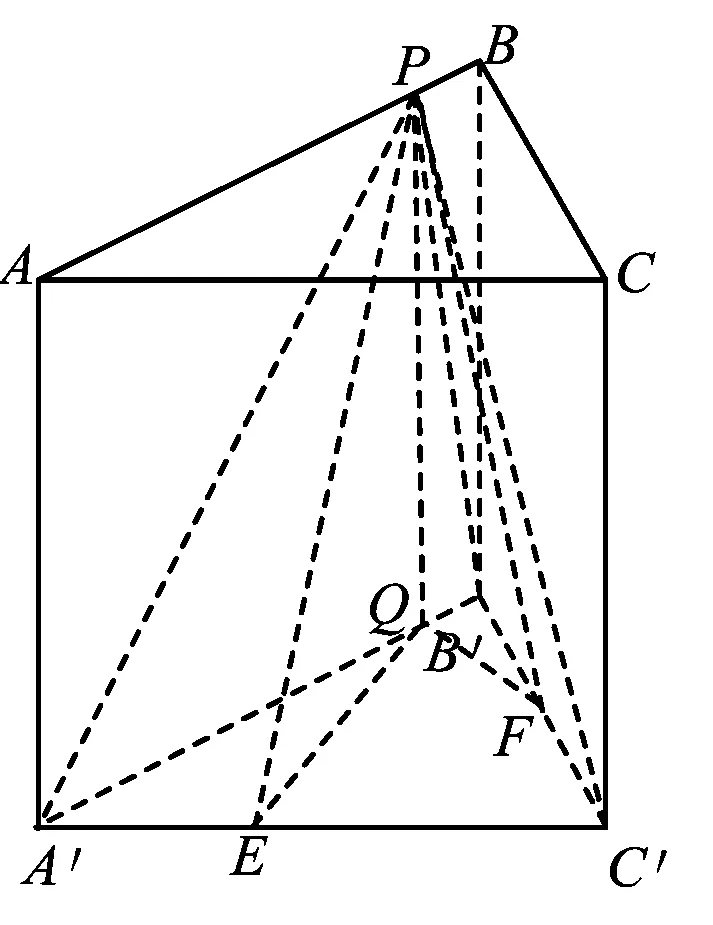
图3
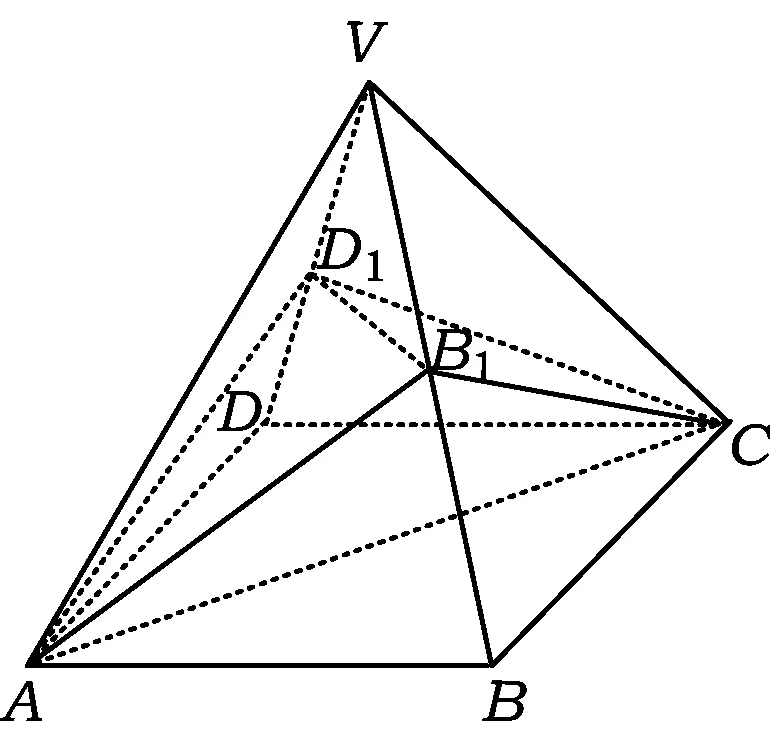
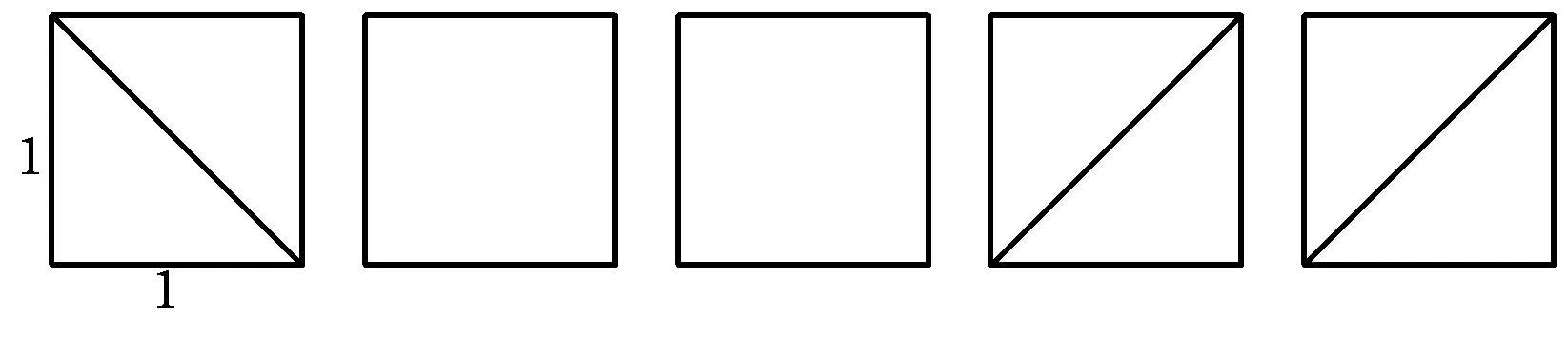
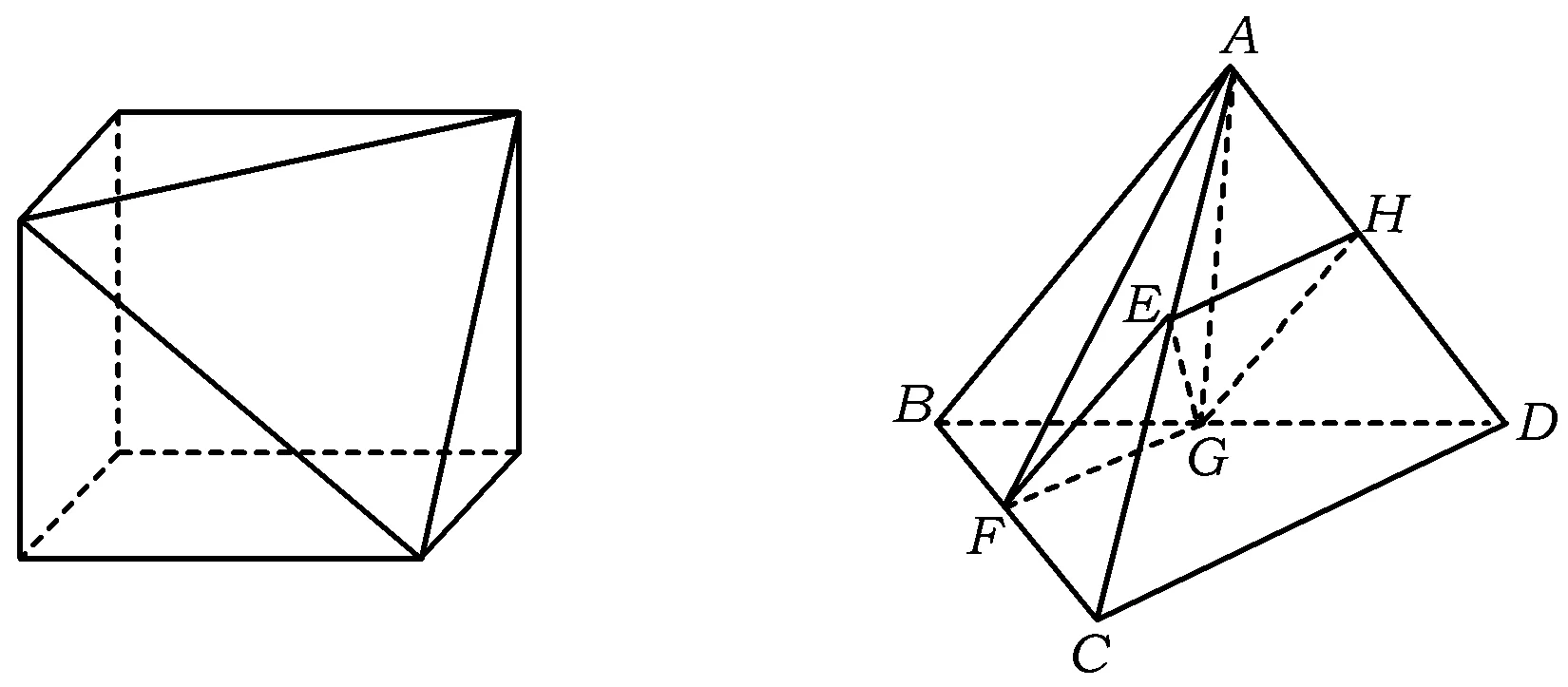
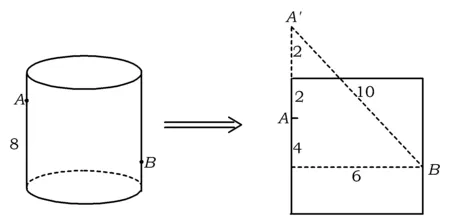
分析如图3,Q为点P在平面AB′C′上的射影,作QE⊥A′C′,QF⊥B′C′,则∠PEQ,∠PFQ分别为二面角P-A′C′-B,P-B′C′-A′的平面角,即∠PEQ=α,∠PFQ=β.设B′Q=x,A′Q=1-x(0 从而 又 于是 评注求二面角的关键是根据已知条件准确地找出或作出要求的角. 例4在三棱柱ABC-A1B1C1中,底面边长与侧棱长均等于2,且E为CC1的中点,则点C1到平面AB1E的距离为 ( ) (2011年同济大学等九校联考试题) 分析本题每个选项中只有一个结果,因此满足条件的任何一个三棱柱中所求距离为同一个数字.不妨取三棱柱ABC-A1B1C1为直三棱柱,如图4所示,运用等体积法,易求得点C1到平面AB1E的距离 故选D. 评注当一般情况不易解决时,要注意把问题特殊化,如特殊数字、特殊函数、特殊图像等,这样可以使解题思路豁然开朗. 例5设ABC-A′B′C′是正三棱柱,底面边长和高都为1,点P是侧面ABB′A的中心,则点P到侧面ACC′A′的对角线的距离是 ( ) 图5 图6 分析如图5,作PQ⊥AC′,则PQ即为所求的距离.将△AB′C′分离出来,作B′E∥PQ,交AC′于点E,取B′C′的中点F,联结AF,如图6.设PQ=h,则 评注空间的距离常转化为平面的距离,而等面积法是求距离的常用方法之一. 例6有一个圆柱形杯子,底面周长为12 cm,高为8 cm,点A在内壁距杯口2 cm处,点A对面外壁距杯底2 cm处有一只小虫,问小虫至少走______cm长的路才能到点A处饱餐一顿? (2009年南京大学自主招生试题) 分析根据题意可将圆柱形杯子展开,如图7所示,小虫从点B到点A′的最短距离可利用勾股定理求得,即为10 cm. 评注几何体的展开是求最短距离的常用办法之一. 图7 ( ). A.32 B.30 C.28 D.26 (2010年复旦大学自主招生试题) 图8 图9 分析如图8为过球心的截面图,设小球的半径为r,依题意有 解得 从而 所放入的小球如图9所示的方式摆放,相邻2个小球的球心B,C与圆心A构成等腰三角形,点D为2个小球的切点,则 从而 ∠CAB≈2×11.95°=23.9°<24°, 评注在解决立体几何问题时,常会遇到若干个球按照一定的法则“叠加”的问题,我们将这类问题简称为“多球”问题.对于“多球”问题,往往可以从多球中提炼出各球球心所组成的图形,将问题简化,然后通过解决该简化的问题,获得原问题的待求结论,这是解决“多球”问题的常用方法之一. 例8半径为R的球内部装4个有相同半径r的小球,则小球半径r的最大值是 ( ) (2009年复旦大学自主招生试题) 图10 因为 AO=R-r, 所以 评注此题也是一个“多球”问题,也可以从多球中提炼出各球球心所组成的立体图形,将问题简化. 例9一个球与正四面体的6条棱都相切,若正四面体的棱长均为a,则这个球的体积为 ( ) 分析设正四面体为P-ABC,O为球心,R为球半径,PO交底面ABC于点D,则点D是△ABC的重心.联结AD,作DE⊥AB于点E,联结OE.在Rt△ODE中, 在Rt△PAD中, 从而 评注球的内接外切问题的关键是分析几何体的特征,根据条件求出球的半径. 例10在四棱锥V-ABCD中,B1,D1分别为侧棱VB,VD的中点,则四面体AB1CD1的体积与四棱锥V-ABCD的体积之比为 ( ) A.1∶6 B.1∶5 C.1∶4 D.1∶3 图11 评注体积问题常常利用“等(同)底等(同)高的体(面)积相等”来求解. 例11设一个多面体从前面、后面、左面、右面、上面看到的图形分别如图12所示,则该多面体的体积为 ( ) (2010年复旦大学自主招生试题) 图12 解联想由正方体变化得到的几何体,如图13所示,其图形即为正方体去掉“一个角”,则 图13 图14 分析设点A到平面DBC的距离为h.在△ABC中,因为AE∶EC=d1∶d2,所以 从而 又因为 VG-AEF=VG-AEH, 评注体积问题是立体几何中的重要问题.在高中数学竞赛与自主招生试题中,利用体积法解题形式简洁,构思容易,内涵深刻,应用广泛,备受青睐.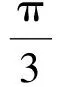
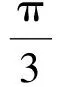
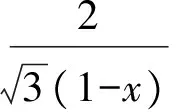
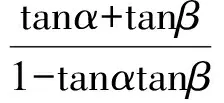


2 距离问题
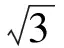
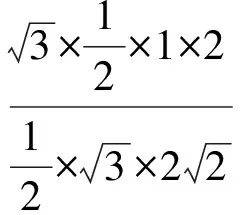

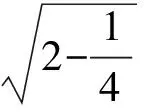

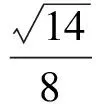
3 内接外切问题



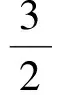

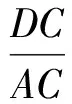

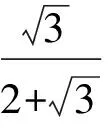
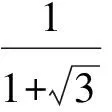
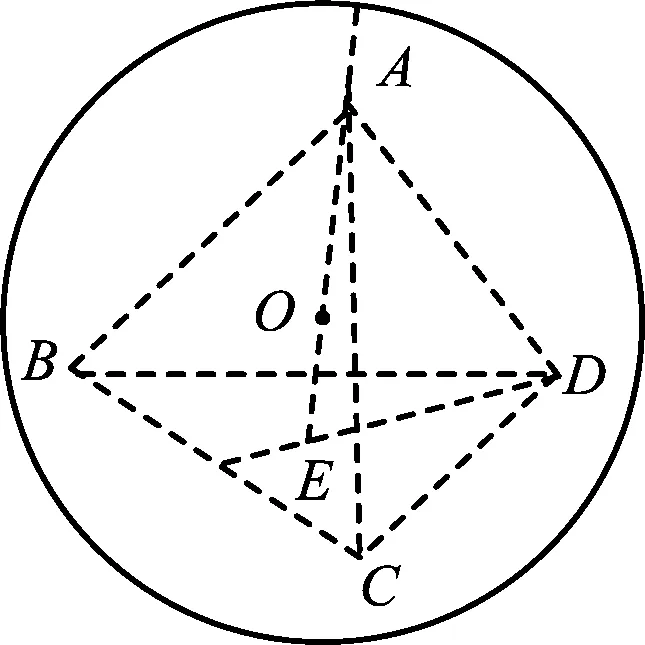
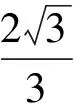

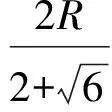
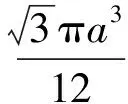
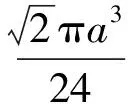
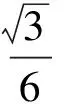
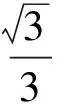
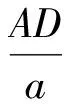

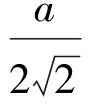
4 体积问题