试题中数学文化的考查举例
——以2013年福建省高三数学质检卷为例
2013-10-26
●
(泉州市第五中学 福建泉州 362000)
试题中数学文化的考查举例
——以2013年福建省高三数学质检卷为例
●杨苍洲
(泉州市第五中学 福建泉州 362000)
《普通高中数学课程标准》在“课程基本理念”中指出:“数学是人类文化的重要组成部分.数学课程应反映数学的历史、应用和发展趋势,数学对推动社会发展的作用,数学的社会需求,社会发展对数学发展的推动作用,数学科学的思想体系,数学的美学价值,数学家的创新精神.数学课程应帮助学生了解数学在人类文明发展中的作用,逐步形成正确的数学观.为此,高中数学课程提倡体现数学的文化价值,并在适当的内容中提出对数学文化的学习要求.”时至今日,课程改革正往纵深的方向推进,走至深处,“文化”才是课程的核心.因此,如何在试题中对数学文化进行考查,以发挥考试指挥棒的作用是命题工作者应该思考的重要问题.
湖北省的高考命题在对数学文化的考查方面作出了很大的努力,如:2009年湖北省文、理科的第10题均以“古希腊人研究的三角形数、正方形数”为背景,理科第15题以“角谷猜想”为背景;2011年湖北省文科第9题、理科第13题以《九章算术》的“竹九节问题”为背景,理科第15题以“斐波那契数列”为背景;2012年湖北省文科第17题以“古希腊毕达哥拉斯学派的三角形数”为背景,理科第10题以《九章算术》中“开立圆术”为背景,理科第13题以“回文数”为背景.
上述大部分试题是以数学史为背景进行命制的.那么,考查数学文化的试题是否也只能以数学史、数学故事为背景进行命制呢?数学文化是否等同于数学史呢?回答是否定的!数学文化并不只是简单的数学史、数学故事、趣味数学,把数学文化等同于数学史的认识是浅薄的、狭隘的.随着数学学科的发生、发展,伴随着数学知识的发生、发展、传播而积蓄下的数学思维方式、数学思想观念及数学精神品格等,这些都属于数学文化.文献[2]把数学文化的内涵概括为:(1)数学的历史;(2)数学的思想;(3)数学的精神;(4)数学与人类其他知识领域之间的关联.下面笔者从这4个角度对2013年福建省高三数学质检卷的个别试题进行剖析,谈谈如何在试题命制中渗透数学文化的考查.
1 渗透数学历史的考查——在故事中得到启迪
数学的历史是数学文化的一部分,这是无可争议的.在数学史中寻找命题背景也一直被命题者所推崇.如果说近几年湖北省的试题隐含着对数学历史的考查,那么下述试题对数学历史的考查则更是深藏不露.
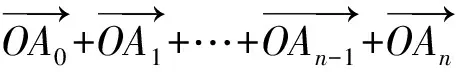
( )
A.5nB.10n
C.5(n+1) D.10(n+1)
例1以平面向量的运算为载体,考查平面向量的加法运算、平面向量的模长、数列求和等基础知识,考查运算求解能力、应用意识、创新意识;考查化归与转化思想、数形结合思想.本题貌似与“数学历史”毫无关联,实则不然,问题速解的思路当来源于我们耳熟能详的“高斯的故事”,即高斯利用“倒序求和”的方法计算“1+2+…+100”.考生若能对“倒序求和”的方法进行迁移应用就能实现对本题的巧解.这种数学史的隐性考查,对考生的应用迁移能力提出了较高的要求.
2 渗透数学思想的考查——在过程中感受思想
过程比结果更重要.若干年后,大部分学生将不再学习数学,当这部分学生不再进行繁杂的数学运算时,数学教学能为他们留下的只有“思想”了,因此,数学思想就是数学文化的重要组成部分.下述试题将为我们展示如何对知识发生、发展过程中所蕴含的数学思想方法进行考查.
例2如图1,A1,A2,…,Am-1(m≥2)为区间[0,1]上的m等分点,直线x=0,x=1,y=0和曲线y=ex所围成的区域为Ω1,图中m个矩形构成的阴影区域为Ω2,在Ω1中任取一点,则该点取自Ω2的概率为______.
例2以“定积分概念形成过程所蕴含的思想——以直代曲”为载体,考查等比数列的前n项求和公式、定积分的概念、几何概型等基础知识;考查运算求解能力、创新意识;考查化归与转化思想、数形结合思想、有限与无限思想.张奠宙教授在文献[3]中谈论了高中文科生学习微积分的意义:“微积分在他们的脑海里,已经跨越初等数学静态的、孤立的思维模式,能用局部与整体的哲学思维动态地进行思考,理解微积分对人类的伟大贡献.这种思考能力,正是现代公民所需要的一种数学文化素质.”本题努力将高中数学教学导向于关注过程、感受思想.
3 渗透数学应用的考查——在生活中实践应用
人教A版高中数学课标教材主编刘绍学先生在主编寄语中说:“数学是有用的、数学是自然的.”如何应用所学数学知识分析和解决生产、生活中的数学问题是学习数学的意义所在.因此,学以致用是数学教学的目标之一,数学应用是数学文化的又一重要组成部分.
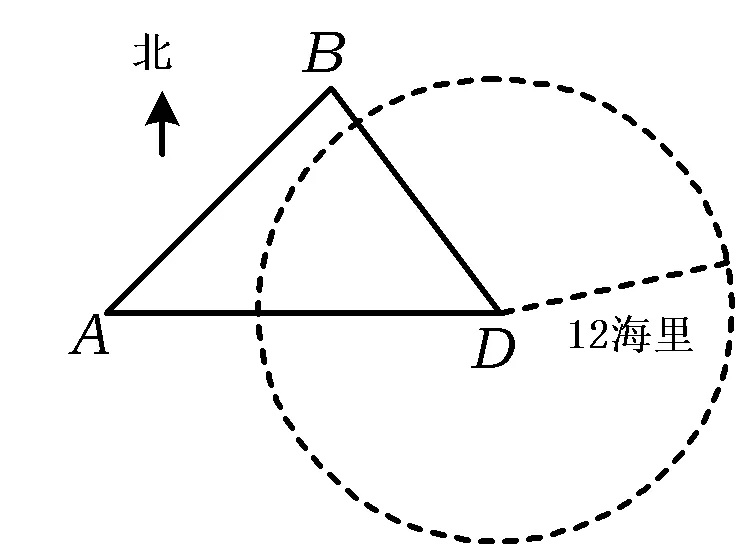
图2
(1)求此时该外国船只与岛D的距离.
(2)观测中发现,此外国船只正以每小时4海里的速度沿正南方向航行.为了将该船拦截在离岛D的12海里处,不让其进入岛D的12海里内海域,试确定海监船的航向,并求其速度的最小值(参考数据:sin36°52′≈0.6,sin53°08′≈0.8).
例3以“海监船维权巡航”为背景,考查余弦定理等基础知识,考查应用意识、运算求解能力,考查化归与转化思想等.“发展学生的数学应用意识”是课标课程的理念之一,同时,课标提出应力求使学生体验数学在解决实际问题中的作用、数学与日常生活及其他学科的联系,促进学生逐步形成和发展数学应用意识,提高实践能力.因此,应用题是考查数学文化的一传统阵地.
4 渗透数学精神的考查——在理性中得以确认
克莱因把数学看成是“一种精神,一种理性精神”,齐民友先生则进一步认为数学精神集中地体现为“彻底的理性探索精神”.当前数学教学往往只是关注数学在知识层面上的应用,而忽视数学精神的教育功能.对数学文化中的理性精神,齐民友先生作出了精辟的论述:“每个论点都必须有根据,都必须持之以理,除了逻辑要求和实践检验外,无论是几千年的习俗、宗教的权威、皇帝的敕令,还是流行的风尚统统是没有用的.”
(1)求椭圆E的方程.
(2)给出命题:“已知P是椭圆E上异于A1,A2的一点,直线A1P,A2P分别交直线l:x=t(t为常数)于2个不同的点M,N,点Q在直线l上.若直线PQ与椭圆E有且只有一个公共点P,则点Q为线段MN的中点”,写出此命题的逆命题,判断你所写出命题的真假,并加以证明.
(3)试研究第(2)小题的结论,根据你的研究心得,在图4中作出与该双曲线有且只有一个公共点S的直线m,并写出作图步骤(注意:所作的直线不能与双曲线的渐近线平行).
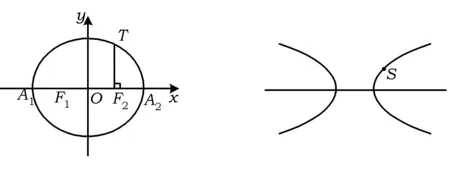
图3 图4
例4主要考查椭圆的标准方程与性质、直线与圆锥曲线的位置关系等基础知识;考查推理论证能力、运算求解能力;考查化归与转化思想、数形结合思想、特殊与一般思想等.“直观感知、演绎证明、操作确认”是数学认识的不同阶段,在第(3)小题中,学生首先要能够从椭圆到双曲线进行正确的类比迁移,从而得到“直观感知”.理性精神是坚持以理性或以理性为基础的思维方法作为判断真假、是非的标准.因此,考生必须研究第(2)小题的结论及其证明过程,同时进行类比推理,虽然这里不需表达出证明的过程,但是考生需要“演绎证明”该心理过程,最后通过动手作图实现“操作确认”,这是一个从感性认识到理性认识的过程.因此,通过本题将引导我们重新审视数学精神的教育价值.
5 与其他关联知识的考查——在交汇中拓宽视野
《考试大纲》明确提出“从学科的整体高度和思维价值的高度考虑问题,在知识网络交汇点设计试题,使对数学基础知识的考查达到必要的深度”的考查要求.知识的交汇大致可以分为学科内的知识交汇和跨学科的知识交汇,学科内的知识交汇能高效地检测学生的基础知识和基本技能,跨学科的知识交汇能有效而全面地检测考生的整体数学素养.因此,在交汇点处设置试题,特别地,在“数学与人类其他知识领域之间的关联”处进行交汇,是考查数学文化的一种有效手段.
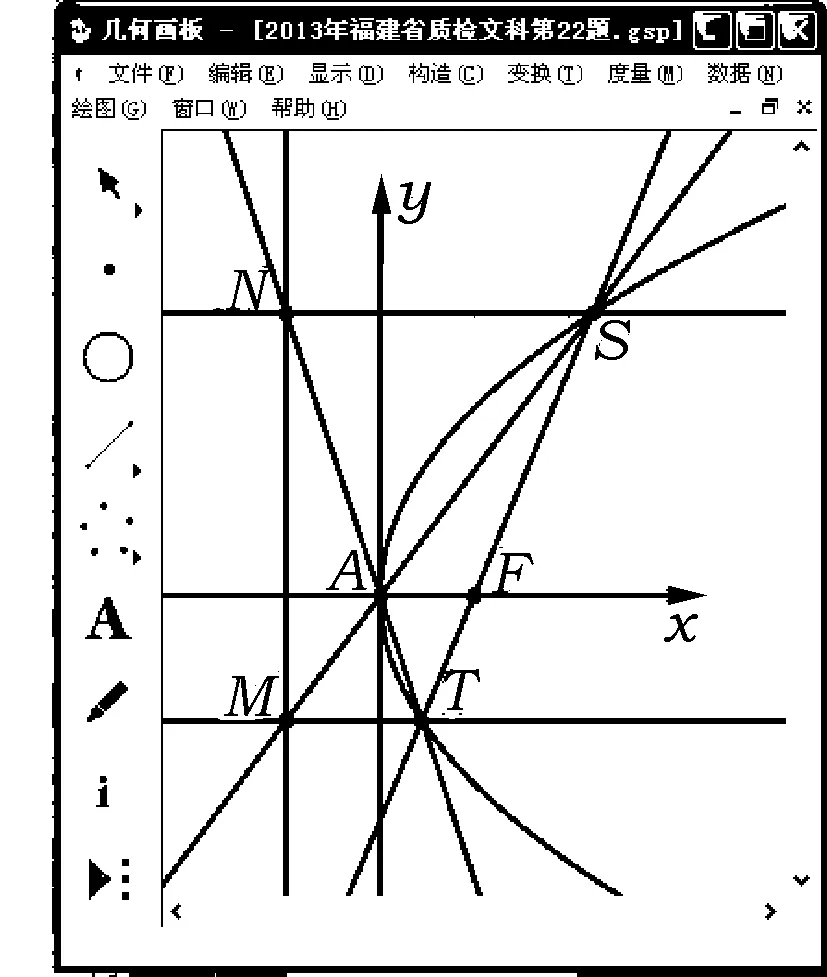
图5
例5如图5,某学生用“几何画板”研究抛物线的性质:打开几何画板软件,绘制抛物线E:y2=2px,在抛物线上任意画一个点S,度量点S的坐标为(xs,ys).
(1)拖动点S,发现当xS=4时,yS=4,试求抛物线E的方程.
(2)设抛物线E的顶点为A,焦点为F,构造直线SF交抛物线E于2个不同的点S,T,构造直线AS,AT分别交准线于点M,N,构造直线MT,NS.经观察得:沿着抛物线E,无论怎样拖动点S,恒有MT∥NS.请你证明这一结论.
(3)为进一步研究该抛物线E的性质,某学生进行了下面的尝试:在第(2)小题中,把“焦点F”改变为其他“定点G(g,0)(g≠0)”,其余条件不变,发现“MT与NS不再平行”.是否可以适当更改第(2)小题中的其他条件,使得仍有“MT∥NS”成立?如果可以,请写出相应的正确命题;否则,说明理由.
例5以“运用几何画板探究抛物线性质”为载体,主要考查抛物线的标准方程、直线与圆锥曲线的位置关系、合情推理等基础知识;考查推理论证能力、运算求解能力;考查化归与转化思想、分类与整合思想、数形结合思想等.体现了在知识的交汇点处命题的指导思想,同时也倡导“注重信息技术与数学课程的整合”的课程理念.
6 结束语
《普通高中数学课程标准》关于课程目标的具体目标之一:“具有一定的数学视野,逐步认识数学的科学价值、应用价值和文化价值,形成批判性的思维习惯,崇尚数学的理性精神,体会数学的美学意义,从而进一步树立辩证唯物主义和历史唯物主义世界观.”
诚然,数学的推理方法、研究方法、思维方式、理性精神等这些都将使一个数学学习者终身受益.数学文化渗透于教学过程已成为数学课程的目标,因此,如何将数学文化自然地渗透于数学试题,将是一个重要的课题.
[1] 中华人民共和国教育部制定.普通高中数学课程标准(实验)[M].北京:人民教育出版社,2003:2-3.
[2] 赵东霞,汪晓勤.关于数学文化教育价值与运用现状的网上调查[J].中学数学月刊,2013(3):41-44.
[3] 张奠宙.《普通高中数学课程标准》的回顾与展望[J].中学数学月刊,2013(3):1-3.
