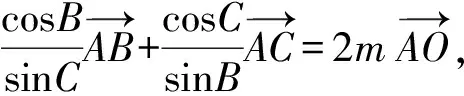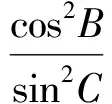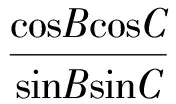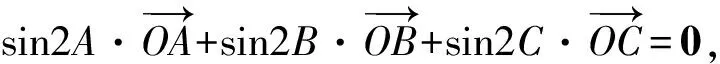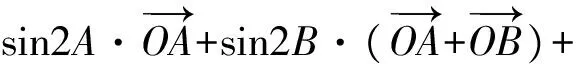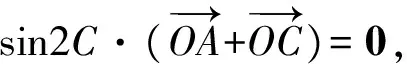释疑纠错归本溯源巧夺天工——高中数学试卷讲评课的3个切入点

●

(孝丰高级中学 浙江安吉 313301)

释疑纠错归本溯源巧夺天工
——高中数学试卷讲评课的3个切入点

●杨爱云

(孝丰高级中学 浙江安吉 313301)

高中数学试卷讲评课在课堂教学中有着举足轻重的地位.面对一份试卷，要立足一节课,如何才能提高试卷讲评的可操作性和时效性，是数学教师普遍关系的一个问题．而今，在试卷讲评时往往侧重于教师的“讲”与“评”，而忽视学生的“感”与“悟”，其效果难以让人满意．笔者的教学实践表明，学生是考试真正的参与者与体验者，试卷讲评应从注重“教师的积极发挥”转移到关注“学生的有效参与”上来．试卷讲评课应以学生为主体，教师要想方设法把试卷中存在的问题巧妙地摆出来，让学生通过独立的思考或通过同伴间的相互讨论、交流与合作而获得真正的解决，因为学生之间的知识结构相近，他们的感知、感悟乃至感叹都感同身受，容易引起思维上的共鸣．这样做，学生印象会更深刻，记忆会更久远，收效也会更全面，远胜于教师的千叮万瞩．下面谈谈笔者的拙见，以飨读者．

1 释疑纠错,落实知识点

解题中的“对”往往出奇的相似，而解题中的“错”却各有各的理由.若考试中出现一定数量“同样的错”则不容小觑，因为其背后可能潜伏着学生“思维上某种错误的默契”．但是对于考试中出现的错，尤其是一些小题的“错误答案”，很难引起教师的关注，教师一般只是用各种方法讲述“正确答案”的由来．由于不明错误症结的源头，仅凭教师的“讲”与“评”，往往收不到好的效果，学生还会重犯．笔者认为，应采用恰当的方法让学生的错误暴露得更充分些，进而让学生在思维碰撞与互动交流中自然释疑纠错、纠偏归正，这可能是一个不错的做法．

案例1已知直线l：kx-y-3k=0，圆M：x2+y2-8x-2y+9=0，则直线与圆的位置关系为

( )

A．相交 B．相切 C．相离 D．由k值确定

这是笔者所在学校期末模拟考卷中的一道选择题，笔者所任教的96名学生中有30人选择答案D．这引起了笔者的警觉．如何揭示与剖析隐藏在错误背后的真正原因呢？解铃还需系铃人，还是要去学生中去探个究竟！以下是课堂再现．

教师：这是考试中的选择题，因为有很多同学都选择了D，那么是否答案就是D了呢？理由是什么呢？

(当教师讲完这句话之后，教室内马上引发一些声音，有些学生希望是批错的，这可以理解，因为学生也希望“加分”．)

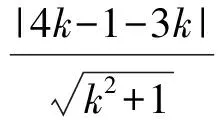
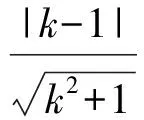
(笔者环视了教室，发现有部分学生与学生1有一样的想法).

学生2：因为直线是不确定的，会随着k的变化而变化，那么直线的具体位置就无法确定，所以与圆的位置关系就无法确定，我也选了D．

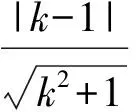
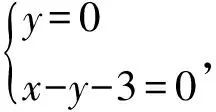
学生3带给我们的不仅是惊喜，还有解题技能与破题的智慧，更给我们带来无尽的回味……，正在咀嚼之际，教室里又传来了声音——

学生4：老师，我觉得学生3的解法可能会出现一个问题，他是取了2个特殊的k值，但是仅仅2个k值就能说明所有的吗？对此我表示怀疑，我是这样想的：由kx-y-3k=0得k(x-3)-y=0，利用直线系的意义，可知这条直线恒过定点(3,0)，后面的思想与学生3一样，故选A．

……

课堂就在学生思维与智慧的相互碰撞中散发出更加理性、更为机智的思想光芒．看来一样的答案不一样的思考确实让我们对试卷讲评的价值重新审视！

2 归本溯源,追寻起始点

案例2已知A,B是抛物线y2=2px(p>0)上的2个点，且OA⊥OB(O为坐标原点)，则直线AB恒过定点

( )

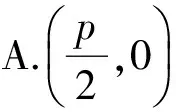
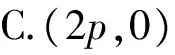
在一次解析几何单元测试中有这样一道选择题，根据学生的测试结果统计，有80%以上的学生选择了A.询问后答案让人啼笑皆非：因为焦点！抛物线中过焦点的弦有很多定值、最值的结论，如何利用这个特殊的位置进行解题，有时可以给解题带来意想不到的效果，但有时使用不当也会让人误入歧途，得不偿失.

探索过程设A(x1,y1)，B(x2,y2),则

由OA⊥OB,得

x1x2+y1y2=0.

又

将y1y2=-x1x2代入，得

因为x1x2≠0，所以

x1x2=4p2，

同理可得

y1y2=-4p2.

又因为y22-y21= (y2-y1)(y2+y1)=

2p(x2-x1),x1≠x2,

所以

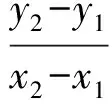
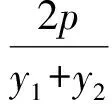
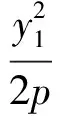
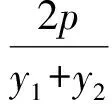
将y1y2=-4p2代入，可得

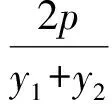
从而直线AB恒过了定点为(2p,0).

特别地，已知抛物线y2=4x与直线y=x-4交于点A,B，求证：OA⊥OB．

探索1过(4，0)的直线与抛物线y2=4x交于点A,B，求证：OA⊥OB.

探索2已知抛物线y2=4px与直线y=x-4p交于点A,B，求证：OA⊥OB.

探索3过点(4p,0)的直线与抛物线y2=4px交于点A,B，求证：OA⊥OB.

探索4若A,B是抛物线y2=2px(p>0)上的2个点，且OA⊥OB(O为坐标原点)，则直线AB恒过定点(2p,0).

考题再现已知过点(4，0)的直线交抛物线y2=2mx(m>0)于点A,B，若∠AOB为锐角，求m的取值范围(答案：m>2,过程略).

同理可得：若∠AOB为钝角时，m的取值范围为0

教学随想从一道选择题我们可以感觉到,解析几何中有很多貌似实异的结论，如果不仔细去探究理解，极易犯“想当然”的错误．现在，许多学生对解析几何问题是“思路想得到，结果做不出”.究其原因，大多是被过程中的运算卡住了壳，这是平时不重视运算所导致的．因此，讲评解析几何问题中“只讲思路分析、轻视运算过程”的现象要加以改变，要多展示中间的解题过程．与此同时，对教材中看似简单实则能体现本源的题目要加以研究，只有深入研究教材，才能真正领会其中的真谛，轻视教材的本源性与重要性都是舍本逐末的做法！

3 巧夺天工,激发兴趣点

思路、方法、技巧是数学试卷讲评课教学的3个关键词．数学的技巧是师生梦寐以求的东西,但“传授”技巧不能“从天而降”，要让学生在熟练掌握方法的基础上自然形成．有位教育专家说:不必为技巧而技巧，用不着的技巧就当收起来，无技巧就是最好的技巧.

由于很少有学生能做出正确答案m=sinθ，笔者认为教师应辅助解决(投影仪展示).

解法1设△ABC的外接圆半径为R，将已知式两边平方得

4m2R2,

利用正弦定理得

又因为 sin2B+sin2C-sin2A=

sin2B+sin2C-sin2(B+C)=

2sinBsinC(sinBsinC-cosBcosC),

所以m2= cos2B+cos2C+2cosBcosC(sinBsinC-

cosBcosC)=

cos2B(1-cos2C)+cos2C(1-cos2B)+

2cosBcosCsinBsinC=

cos2Bsin2C+cos2Csin2B+

2cosBcosCsinBsinC=

(sinBcosC+cosBsinC)2=

sin2(B+C)=sin2A,

注意到m>0,sinA>0，故m=sinθ．

教学随想笔者认为以上解法虽看似复杂，但有很大的技巧性;虽极为巧妙，但很不自然，需要学生有一定的恒心和毅力，

利用熟知的三角形恒等式sin2A+sin2B+sin2C=4sinAsinBsinC及正弦二倍角公式得

从而

故

m=sinA=sinθ．

解法揭示了本题的命题背景,本题的一般情形是三角形的如下2个性质：

(1)设O是△A1A2A3内任意一点，则

(2)设O是△A1A2A3外一点且在∠A2A1A3内，则

数学试卷的讲评课，既不能成为解题失败者“忏悔”的场所，也不应单单是解题成功者“表演”的舞台．要使各个层面的学生有所获，让数学后进生感到“暗中有光”，中等生感觉“对中有优”，尖子生感叹“山外有山”！教学实践表明，由学生经历过“感”、“悟”的试卷讲评课才是真正解决问题的试卷讲评方式，只有这样，才能让学生的困难得到暴露，知识得到落实，智慧在一定程度上才能有所启迪！

[1] 殷玉波．试卷讲评的“宏观调控”策略．中学数学教学教学参考[J]，2012(5)：39-40．

[2] 陆贤彬,朱占奎．联系 拓展 创新——高考模拟试卷讲评的一种尝试[J]．中学数学教学参考，2012(5)：42-43．

[3] 高莉芳．一堂数列习题课的案例分析[J]．中学数学月刊，2010(5)：16-18．